Introduction to the concept of entropy and its many faces

As it may seem, the analysis of signals and data is a topic well enough studied and has already been spoken hundreds of times. But there are some failures in it. In recent years, the word "entropy" rushes all and sundry, plainly and not understanding what they are talking about. Chaos - yes, disorder - yes, in thermodynamics it is used - it seems like yes too, with reference to signals - and then yes. I would like at least to clarify this moment a bit and give direction to those who want to know a little more about entropy. Let's talk about the entropy data analysis.

Russian-language sources have very little literature on this subject. And a whole idea is almost impossible to get at all. Fortunately, my scientific leader was just a connoisseur of entropy analysis and the author of a fresh monograph [1], where everything is written "from and to". Fortunately there was no limit, and I decided to try to convey thoughts on this subject to a wider audience, so I'll take a couple of extracts from the monograph and supplement it with my own research. Maybe someone will come in handy.

So let's start from the beginning. Shannon in 1963 proposed the concept of a measure of the average informativeness of the test (the unpredictability of its outcomes), which takes into account the probability of individual outcomes (before it was Hartley, but this is omitted). If the entropy is measured in bits, and take the base 2, then we get the formula for the Shannon entropy
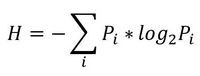where Pi is the probability of the i-th outcome.

That is, in this case, entropy is directly related to the “surprise” of the occurrence of an event. And from this follows its information content - the more predictable an event, the less informative it is. This means that its entropy will be lower. Although the question remains open about the relationship between the properties of information, the properties of entropy and the properties of its various estimates. Just with the estimates we are dealing in most cases. All that can be investigated is the informativeness of various entropy indices regarding controlled changes in the properties of processes, i.e. in essence, their usefulness for solving specific applied problems.
')
The entropy of a signal described in some way (i.e. deterministic) tends to zero. For random processes, the entropy increases the more, the higher the level of "unpredictability". Perhaps it is precisely from such a bunch of interpretations of entropy that probability-> unpredictability-> informativeness implies the concept of “chaos”, although it is rather vague and vague (which does not prevent its popularity). There is also the identification of entropy and complexity of the process. But this is again not the same thing.

We go further.

Entropy is a different black white red :

• thermodynamic
• algorithmic
• informational
• differential
• topological

They all differ on the one hand, and have a common basis on the other. Of course, each type is used to solve certain problems. And, unfortunately, even in serious works there are errors in the interpretation of the calculation results. And everything is connected with the fact that in practice in 90% of cases we deal with a discrete representation of a signal of continuous nature, which significantly affects the entropy estimate (in fact, there appears a correction factor in the formula that is usually ignored).

In order to slightly describe the areas of application of entropy to data analysis, consider a small applied problem from the monograph [1] (which is not in digital form, and most likely will not).

Let there be a system that switches between several states every 100 clock cycles and generates a signal x (Figure 1.5), the characteristics of which change during the transition. But what - we do not know.

By breaking x into realizations of 100 samples, one can construct an empirical distribution density and calculate the value of Shannon's entropy from it. We get the values ​​“separated” by levels (Figure 1.6).



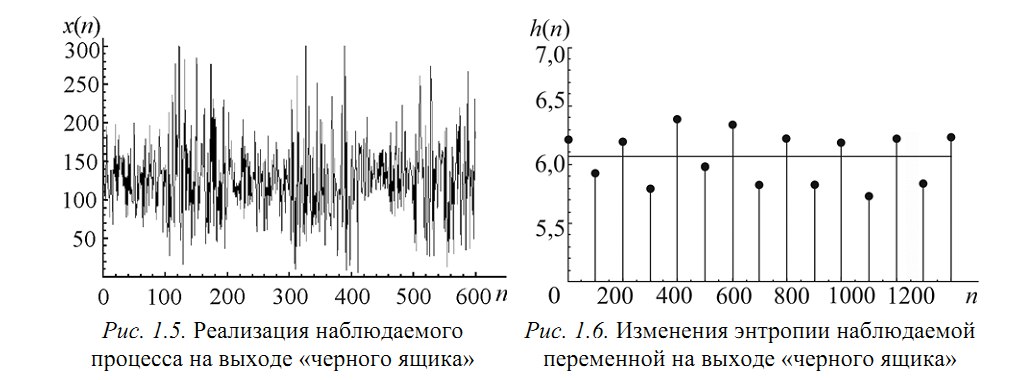
As you can see, the transitions between states are clearly observed. But what to do if the transition time is not known to us? As it turned out, the calculation by the sliding window can help and entropy also “spreads” to the levels. In a real study, we used this effect to analyze the EEG signal (multi-colored pictures about it will be further).

Now about one more entertaining property of entropy - it allows us to estimate the degree of connectedness of several processes . If they have the same sources, we say that the processes are related (for example, if an earthquake is fixed in different parts of the Earth, then the main component of the signal on the sensors is common). In such cases, correlation analysis is usually used, but it works well only to identify linear relationships. In the case of non-linear (generated by time delays, for example), we suggest using entropy.

Consider a model of 5 hidden variables (their entropy is shown in the figure below on the left) and 3 observables that are generated as a linear sum of hidden variables taken with time shifts according to the scheme shown below on the right. Numbers are coefficients and time shifts (in readings).



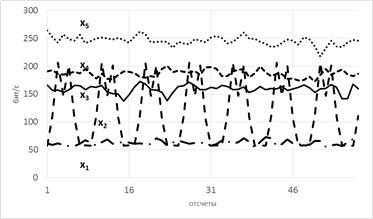
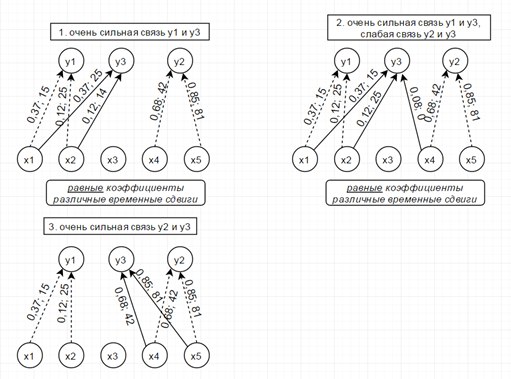
So, the trick is that the entropy of connected processes comes closer with the strengthening of their connection. Damn, how beautiful it is!



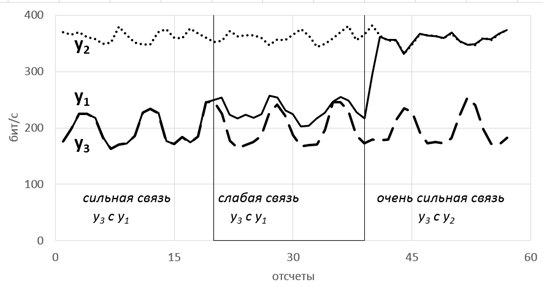
Such joys make it possible to pull out almost any of the strangest and most chaotic signals (especially useful in economics and analytics) for more information. We pulled them out of the electroencephalogram, considering the fashionable now Sample Entropy and here are some pictures.



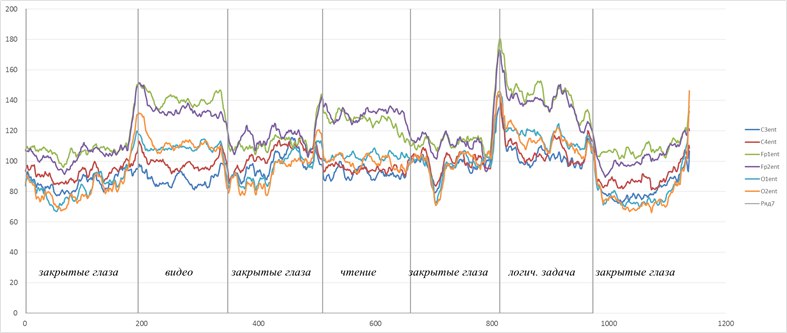
It can be seen that the entropy jumps correspond to a change in the stages of the experiment. There are a couple of articles on this topic and the master’s is already defended, so if anyone is interested in the details, I’ll be happy to share. And so on the world by the entropy EEG have been looking for different things for a long time - the stages of anesthesia, sleep, Alzheimer's and Parkinson's disease, the effectiveness of treatment for epilepsy is considered and so on. But again, often the calculations are carried out without taking into account the correction factors, and this is sad, since the reproducibility of research is a big question (which is critical for science, so).

Summarizing, I will dwell on the universality of the entropy apparatus and its actual effectiveness, if we approach everything with regard to pitfalls. I hope that after reading you will have a seed of respect for the great and mighty power of Entropy.

PS If there is interest, I can talk a little more about the next time about the algorithms for calculating the entropy and why the Shannon entropy is now shifted by more recent methods.
PPS Continuation about local-rank coding see here.

Literature

1. Tsvetkov OV Entropy data analysis in physics, biology and technology. SPb .: Publishing house of Saint-Petersburg Electrotechnical University "LETI", 2015. 202 p. www.polytechnics.ru/shop/product-details/370-cvetkov-ov-entropijnyj-analiz-dannyx-v-fizike-biologii-i-texnike.html
2. Abasolo D., Hornero R., Espino P. Entropy analysis of the EEG background activity in Alzheimer's disease patients // Physiological Measurement. 2006. Vol. 27 (3). P. 241 - 253. epubs.surrey.ac.uk/39603/6/Abasolo_et_al_PhysiolMeas_final_version_2006.pdf
3. 28. Bruce Eugene N, Bruce C Margaret C, Vennelaganti S. Eg. 2009. Vol. 26 (4). P. 257 - 266. www.ncbi.nlm.nih.gov/pubmed/19590434
4. Entropy analysis as a method for the non-hypothetical search for real (homogeneous) social groups (O. I. Shkaratan, G.A.
5. Entropy and other systemic laws: Issues of managing complex systems. Prangishvili I.V. apolov-oleg.narod.ru/olderfiles/1/Prangishvili_I.V_JEntropiinye_i_dr-88665.pdf