Self-learning chess program
Hello, Habr!
In an article published last year , we solved the problem of determining the mathematically justified values of chess pieces. With the help of regression analysis of parties played by computers and people, we managed to get the value scale of “units”, which largely coincides with the traditional values known from books and practical experience.
Unfortunately, the direct substitution of the corrected values for the figures did not strengthen the author's program - in any case, more than within the framework of statistical error. The application of the original method "in the forehead" to other parameters of the evaluation function yielded somewhat absurd results, the optimization algorithm clearly needed some refinement. Meanwhile, the author decided that the next release of his engine will be the final in a long series of versions originating in the code of a decade ago. GreKo version 2015 was released, and no further changes were planned in the near future.
')
All interested in what happened next - after viewing the picture to attract attention, welcome to the cat.
The motivation for the sudden continuation of the work and, ultimately, the appearance of this article were two events. One of them thundered to the whole world through the media channels - this is the match in Go of the Korean top player Lee Sedol with the Google AlphaGo program.
The developers at Google DeepMind were able to effectively combine two powerful techniques - searching in the tree using the Monte Carlo method and deep learning using neural networks. The resulting symbiosis led to phenomenal results in the form of a victory over two professional players in Guo (Lee Cedol and Fan Hue) with a total score of 9 - 1. The details of the implementation of AlphaGo were widely discussed, including on Habré, so now we will not dwell on them.
The second event, not so widely advertised, and seen mainly by chess-programming enthusiasts, is the emergence of the Giraffe program. Its author, Matthew Lai, actively used the ideas of machine learning, in particular, all the same deep neural networks. Unlike traditional engines, in which the evaluation function contains a number of predefined characteristics of the position, Giraffe at the training stage independently extracts these signs from the educational material. In fact, the goal of the automatic derivation of “chess knowledge” in the form in which it is presented in textbooks was stated.
In addition to the evaluation function, neural networks in Giraffe were also used to parameterize the search in a tree, which also suggests some parallels with AlphaGo.
The program has demonstrated some success, having reached from scratch in a few days of training the strength of an international master. But, unfortunately, the most interesting research project was prematurely completed ... in connection with the transition of Matthew Lai to work in the Google DeepMind team!
Anyway, the information wave that arose in connection with AlphaGo and Giraffe, prompted the author of this article to once again return to the code of his engine and still try to strengthen his game with the methods of machine learning that is so popular today.
It may disappoint someone, but in the project described there will be neither multilayered neural networks, nor automatic detection of key position attributes, nor the Monte Carlo method. Random search for wood in chess is practically not required due to the limited task, and well-functioning factors for evaluating the chess position have been known since the days of Kaissa . In addition, the author was interested in how you can enhance the game of the program within a fairly minimalist set of them, which is implemented in GreKo.
The basic method was the algorithm for setting the evaluation function, which was proposed by the Swedish researcher and developer Peter Österlund, the author of the strong Texel program. The winning sides of this method, according to its creator, are:
Let θ = (θ 1 , ..., θ K ) be the vector of parameters of the evaluation function (weight of the material and positional features).
For each position p i , i = 1 ... N from the test set, we calculate its static estimate E θ (p i ) , which is a certain scalar value. Traditionally, the assessment is rationed so that it gives an idea of the advantage of one side or the other in units of chess material - for example, hundredths of a pawn. We will always consider the evaluation in terms of whites.
We now turn from the material representation of the estimate to the probabilistic one. Using the logistic function, we will do the following conversion:
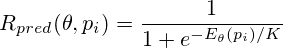
The value of R pred makes sense of the mathematical expectation of the result of the game for white in this position (0 is a defeat, 0.5 is a draw, 1 is a victory). The normalization constant K can be defined as such a material advantage, in which "everything becomes clear." In this study, we used the value K = 150 , i.e. one and a half pawns. Of course, “it becomes clear” only in a statistical sense, in real chess games one can find a huge number of counterexamples, when a much greater material advantage does not lead to a gain.
In the original algorithm, instead of a static evaluation function, the result of the so-called PV search was used to calculate R pred . The name is associated with the concept of the forced version, in the English version - quiescence search. This is an alpha-beta search from a given position in which only captures, transformations of pawns, and sometimes shahs and departures from them are considered. Although the search trees are small, compared to the static estimate, the computation speed decreases by tens and hundreds of times. Therefore, it was decided to use a faster scheme, and sift out dynamic positions at the stage of preparing the initial data.
Now, knowing for each position the predicted R pred and actual R fact results of the game in which it met, we can calculate the root-mean-square prediction error:
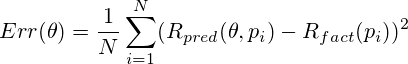
In fact, the obtained rms estimate can already be considered as the objective functional to be minimized. This approach is described in the original description of the method.
We will make another small modification - we introduce the accounting of the number of moves remaining until the end of the game. Obviously, a positional sign that existed on the board at the very beginning of the game may not have any effect on its outcome if the main events in the game occurred much later. For example, White in the opening may have a proud knight in the center of the board, but lose in the deep endgame, when this knight is already long traded, due to the invasion of the enemy rook into his camp. In this case, the sign “a horse in the center of the board” should not receive too much punishment compared to the sign “a rook on the second rank” - the horse is not to blame for anything!
Accordingly, we add an amendment to our objective function related to the number of moves n i remaining until the end of the game. For each position, it will be an exponential decay factor with the parameter λ . The “physical meaning” of this parameter is the number of moves during which a particular positional attribute influences the game. Again, on average. In the experiments described below, λ takes values in several dozen half-moves.
In the original description of Texel's Tuning Method from the training set, the first moves in the batches were discarded. The introduction of " λ- forgetting" allows us not to impose a clear restriction on the moves from the opening book - their influence somehow turns out to be small.
The final view of our target functionality:
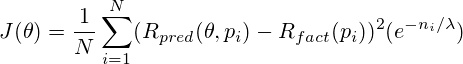
The task of learning the evaluation function is now reduced to minimizing J in the space of values of the vector θ .
Why does this method work? In fact, most of the signs arising in positions on large batches of parties, due to averaging, are mutually neutralized. Only those of them that actually influenced the result retain their value and receive higher weights. The sooner the evaluation function starts to notice them during the game - the better the prediction and the more accurate the position estimate, the stronger the program will become.
As an array of data for training, positions from 20 thousand games played with the program were used. From their number were excluded positions arising after the capture of a figure or the announcement of the Shah. This is necessary so that the training set of examples matches as closely as possible with the actual positions from the search tree, for which static evaluation is applied.
The result was about 2.27 million positions. They are not all unique, but this is not critical for the method used. Positions were randomly divided into training and test sets in the ratio of 80/20, respectively 1.81 million and 460 thousand positions.
The minimization of the functional was carried out on a training set by the method of coordinate descent. It is known that for multi-dimensional optimization problems this method is usually not the best choice. However, the simplicity of the implementation, as well as an acceptable execution time, played in favor of this algorithm. On a typical modern PC, optimization for 20 thousand batches takes from one to several hours, depending on the subset of 27 possible weights selected for tuning.
Below is a graph of functional changes depending on time. The criterion for stopping the training is the non-improvement of the result for the test subset after the next cycle of descents in all parameters.
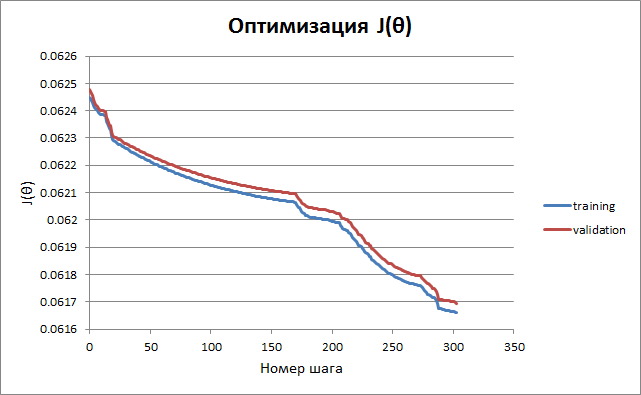
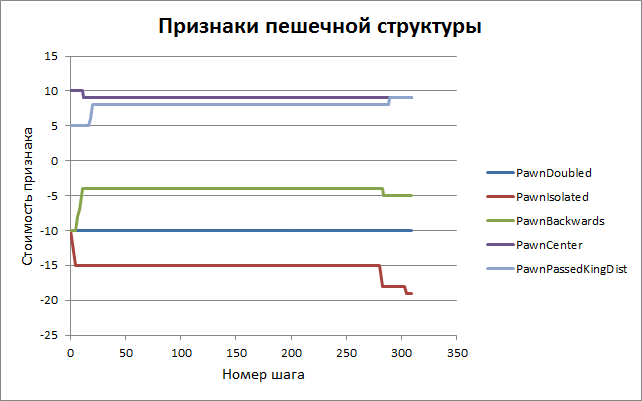
The evolution of a group of parameters related to pawns is shown in the following graph. It can be seen that the process converges quickly enough - at least to a local minimum. The task of searching for a global minimum has not yet been set, our goal now is to strengthen the program by at least some amount ...
We give a complete list of evaluation parameters with initial and final values. The meaning of the most part is clear without additional comments, those who wish to familiarize themselves with their exact purpose are invited to the source code of the program - the eval.cpp file, the Evaluate () function.
The table shows an example for one of the training sessions, in which only the positional parameters of the evaluation were optimized, and the cost of the figures remained unchanged. This is not a critical requirement; in the tests described below, full training on all 27 parameters was used. But the best results in the practical game showed a version with a constant scale of material.
What conclusions can be drawn from the weights obtained? It can be seen that some of them have remained almost unchanged compared with the original version of the program. It can be assumed that over the years of debugging the engine, they were selected intuitively enough. However, at some points, cold mathematics amended human intuition. So, the damage of the backward pawns was overrated by the author. But the following parameters seemed more important to the algorithm, their weights were almost doubled:
We should also mention the sign of the checkpoint, which is unattainable according to the “rule of the square”. Its optimized value has reached the limit of the acceptable interval set by the algorithm. Obviously, it could be more. The reason, probably, is that in the training file, in the presence of such a passing pawn, the games were won 100% of the time. As a weight, the value of 200 was left as quite sufficient - its increase has practically no effect on the strength of the game.
So, we have trained the evaluation function to predict the outcome of the game based on the position on the board. But the main test lies ahead - how much this skill will prove useful in a practical game. For this purpose, several versions of the engine with different settings were prepared, each of which was obtained in its own training mode.
20000.pgn - program parts with itself (superblits)
gm2600.pgn - grandmasters' games from the Crafty Robert Hyatt FTP site (classic control)
large.pgn - merge the two files
Each of the versions played 100 games with the original program GreKo 2015, as well as with a set of other engines with time control "1 second + 0.1 seconds per turn". The results are shown in the table below. With the help of the program bayeselo, relative ratings of versions were calculated, the power of GreKo 2015 was fixed as a reference point at the level of 2600. The value of LOS (likelihood of superiority) was also determined - the probability that a particular version plays stronger than GreKo 2015 taking into account the confidence interval of rating calculation.
It is seen that the improvement of the game occurred in all cases except one (version D). It is also interesting that training in the games of grandmasters (version G) had a slight effect. But the addition to the games of grandmasters of their own games of the program, plus the modification of the values of the pieces (version H2) turned out to be a fairly successful combination.
The strongest in the aggregate of results was version C, with an increase in the rating of about 70 points. For a given number of batches, this margin is statistically significant, the error is plus or minus 30 points.
We trained and tested the program at ultra-short time control, when one batch lasts a few seconds. Check how our improvements work in the "serious" game, with longer controls.
So, despite a slight drop in efficiency with an increase in the length of the games, the trained version definitely demonstrates a stronger game than the engine with the original settings. She was released as another final release of the program.
The GreKo 2015 ML program can be freely downloaded along with the source code in C ++. It is a console application for Windows or Linux. To play with a person, analyze or spar with other engines, you may need a graphical interface - for example, Arena, Winboard, or some other. However, you can play directly from the command line, introducing moves using standard English notation.
GreKo's self-learning function is implemented as a built-in command of the console mode (the author currently does not know other engines that support this functionality). The vector of 27 coefficients of the evaluation function is stored in the file weights.txt. To automatically adjust it based on a PGN file, you need to type the command learn, for example:
The program will read all batches from the specified file, create an intermediate file with training positions and break it into a training and test subset:
It will then save the original values of the parameters to the weights.old file, and begin the optimization process. During operation, intermediate values of weights and target functionality are displayed on the screen and in the file learning.log.
Upon completion of the training, the weights.txt file will contain the new values of the weights, which will take effect the next time the program is launched.
The learn command can contain two more arguments, the lower and upper bounds of the optimization interval. By default, they are 6 and 27 - i.e. all signs, except the cost of figures, are optimized. To enable full optimization, you must specify the boundaries explicitly:
The algorithm is randomized (in terms of splitting into training and test samples), therefore, for different starts unequal vectors of coefficients can be obtained.
To configure the evaluation function, we used self-learning program (reinforcement learning). The best results were achieved by analyzing the games of the program against itself. In fact, the only external source of chess knowledge was the opening book of the shell, necessary for the randomization of the games played.
We were able to increase the predictive ability of the assessment, which led to a statistically significant increase in the strength of the game at different time controls, both with the previous version and with a set of independent opponents. The improvement was 50 ... 70 points Elo.
It is worth noting that the result was achieved in fairly modest volumes: about 20 thousand parties and 1 million positions (for comparison: AlphaGo studied on 30 million positions from parties of strong amateurs from the server, not counting further games with herself). The evaluation function of GreKo is also very simple, and includes only 27 independent parameters. In the strongest chess engines, their score can go on hundreds and thousands. However, even in such an environment, machine learning methods led to success.
Further improvement of the program could include adding new criteria to the evaluation function (in particular, taking into account the stage of the game for all the considered parameters) and using more advanced methods of multidimensional optimization (for example, searching for global extremes). At the moment, however, the author’s plans in this direction have not yet been determined.
In an article published last year , we solved the problem of determining the mathematically justified values of chess pieces. With the help of regression analysis of parties played by computers and people, we managed to get the value scale of “units”, which largely coincides with the traditional values known from books and practical experience.
Unfortunately, the direct substitution of the corrected values for the figures did not strengthen the author's program - in any case, more than within the framework of statistical error. The application of the original method "in the forehead" to other parameters of the evaluation function yielded somewhat absurd results, the optimization algorithm clearly needed some refinement. Meanwhile, the author decided that the next release of his engine will be the final in a long series of versions originating in the code of a decade ago. GreKo version 2015 was released, and no further changes were planned in the near future.
')
All interested in what happened next - after viewing the picture to attract attention, welcome to the cat.
The motivation for the sudden continuation of the work and, ultimately, the appearance of this article were two events. One of them thundered to the whole world through the media channels - this is the match in Go of the Korean top player Lee Sedol with the Google AlphaGo program.
The developers at Google DeepMind were able to effectively combine two powerful techniques - searching in the tree using the Monte Carlo method and deep learning using neural networks. The resulting symbiosis led to phenomenal results in the form of a victory over two professional players in Guo (Lee Cedol and Fan Hue) with a total score of 9 - 1. The details of the implementation of AlphaGo were widely discussed, including on Habré, so now we will not dwell on them.
The second event, not so widely advertised, and seen mainly by chess-programming enthusiasts, is the emergence of the Giraffe program. Its author, Matthew Lai, actively used the ideas of machine learning, in particular, all the same deep neural networks. Unlike traditional engines, in which the evaluation function contains a number of predefined characteristics of the position, Giraffe at the training stage independently extracts these signs from the educational material. In fact, the goal of the automatic derivation of “chess knowledge” in the form in which it is presented in textbooks was stated.In addition to the evaluation function, neural networks in Giraffe were also used to parameterize the search in a tree, which also suggests some parallels with AlphaGo.
The program has demonstrated some success, having reached from scratch in a few days of training the strength of an international master. But, unfortunately, the most interesting research project was prematurely completed ... in connection with the transition of Matthew Lai to work in the Google DeepMind team!
Anyway, the information wave that arose in connection with AlphaGo and Giraffe, prompted the author of this article to once again return to the code of his engine and still try to strengthen his game with the methods of machine learning that is so popular today.
Algorithm
It may disappoint someone, but in the project described there will be neither multilayered neural networks, nor automatic detection of key position attributes, nor the Monte Carlo method. Random search for wood in chess is practically not required due to the limited task, and well-functioning factors for evaluating the chess position have been known since the days of Kaissa . In addition, the author was interested in how you can enhance the game of the program within a fairly minimalist set of them, which is implemented in GreKo.
The basic method was the algorithm for setting the evaluation function, which was proposed by the Swedish researcher and developer Peter Österlund, the author of the strong Texel program. The winning sides of this method, according to its creator, are:
- The ability to simultaneously optimize up to several hundred parameters of the evaluation function.
- The absence of a need for a source of “external knowledge” in the form of expert assessments of positions — only texts and the results of parties are needed.
- Correct work with strongly correlated signs - no preliminary preparation like their orthogonalization is required.
Let θ = (θ 1 , ..., θ K ) be the vector of parameters of the evaluation function (weight of the material and positional features).
For each position p i , i = 1 ... N from the test set, we calculate its static estimate E θ (p i ) , which is a certain scalar value. Traditionally, the assessment is rationed so that it gives an idea of the advantage of one side or the other in units of chess material - for example, hundredths of a pawn. We will always consider the evaluation in terms of whites.
We now turn from the material representation of the estimate to the probabilistic one. Using the logistic function, we will do the following conversion:
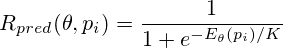
The value of R pred makes sense of the mathematical expectation of the result of the game for white in this position (0 is a defeat, 0.5 is a draw, 1 is a victory). The normalization constant K can be defined as such a material advantage, in which "everything becomes clear." In this study, we used the value K = 150 , i.e. one and a half pawns. Of course, “it becomes clear” only in a statistical sense, in real chess games one can find a huge number of counterexamples, when a much greater material advantage does not lead to a gain.
In the original algorithm, instead of a static evaluation function, the result of the so-called PV search was used to calculate R pred . The name is associated with the concept of the forced version, in the English version - quiescence search. This is an alpha-beta search from a given position in which only captures, transformations of pawns, and sometimes shahs and departures from them are considered. Although the search trees are small, compared to the static estimate, the computation speed decreases by tens and hundreds of times. Therefore, it was decided to use a faster scheme, and sift out dynamic positions at the stage of preparing the initial data.
Now, knowing for each position the predicted R pred and actual R fact results of the game in which it met, we can calculate the root-mean-square prediction error:
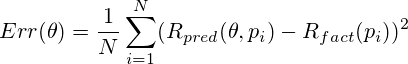
In fact, the obtained rms estimate can already be considered as the objective functional to be minimized. This approach is described in the original description of the method.
We will make another small modification - we introduce the accounting of the number of moves remaining until the end of the game. Obviously, a positional sign that existed on the board at the very beginning of the game may not have any effect on its outcome if the main events in the game occurred much later. For example, White in the opening may have a proud knight in the center of the board, but lose in the deep endgame, when this knight is already long traded, due to the invasion of the enemy rook into his camp. In this case, the sign “a horse in the center of the board” should not receive too much punishment compared to the sign “a rook on the second rank” - the horse is not to blame for anything!
Accordingly, we add an amendment to our objective function related to the number of moves n i remaining until the end of the game. For each position, it will be an exponential decay factor with the parameter λ . The “physical meaning” of this parameter is the number of moves during which a particular positional attribute influences the game. Again, on average. In the experiments described below, λ takes values in several dozen half-moves.
In the original description of Texel's Tuning Method from the training set, the first moves in the batches were discarded. The introduction of " λ- forgetting" allows us not to impose a clear restriction on the moves from the opening book - their influence somehow turns out to be small.
The final view of our target functionality:
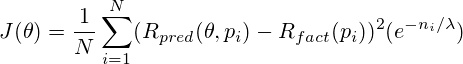
The task of learning the evaluation function is now reduced to minimizing J in the space of values of the vector θ .
Why does this method work? In fact, most of the signs arising in positions on large batches of parties, due to averaging, are mutually neutralized. Only those of them that actually influenced the result retain their value and receive higher weights. The sooner the evaluation function starts to notice them during the game - the better the prediction and the more accurate the position estimate, the stronger the program will become.
Training and Results
As an array of data for training, positions from 20 thousand games played with the program were used. From their number were excluded positions arising after the capture of a figure or the announcement of the Shah. This is necessary so that the training set of examples matches as closely as possible with the actual positions from the search tree, for which static evaluation is applied.
The result was about 2.27 million positions. They are not all unique, but this is not critical for the method used. Positions were randomly divided into training and test sets in the ratio of 80/20, respectively 1.81 million and 460 thousand positions.
The minimization of the functional was carried out on a training set by the method of coordinate descent. It is known that for multi-dimensional optimization problems this method is usually not the best choice. However, the simplicity of the implementation, as well as an acceptable execution time, played in favor of this algorithm. On a typical modern PC, optimization for 20 thousand batches takes from one to several hours, depending on the subset of 27 possible weights selected for tuning.
Below is a graph of functional changes depending on time. The criterion for stopping the training is the non-improvement of the result for the test subset after the next cycle of descents in all parameters.
The evolution of a group of parameters related to pawns is shown in the following graph. It can be seen that the process converges quickly enough - at least to a local minimum. The task of searching for a global minimum has not yet been set, our goal now is to strengthen the program by at least some amount ...
Similar graphs for other features.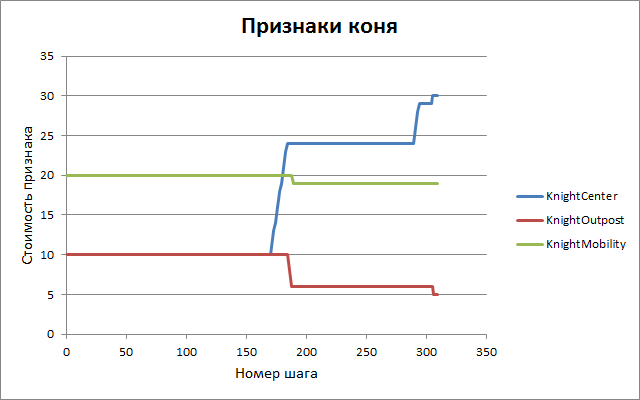
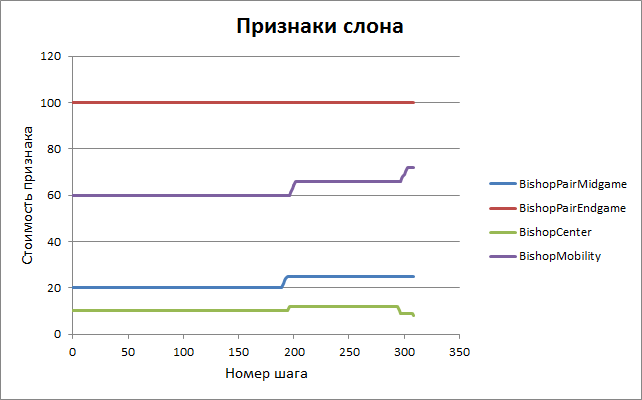
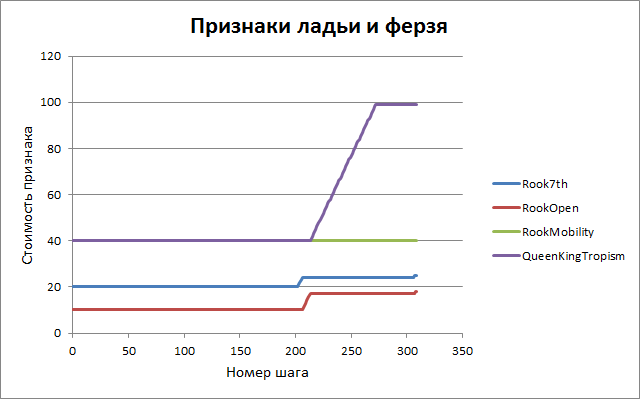
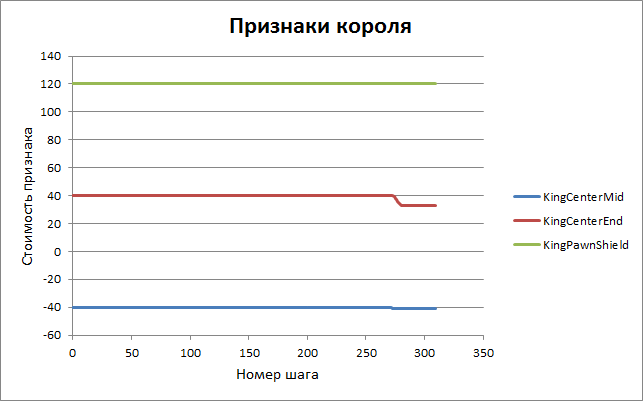
The following graph presents data related to another training session in which material weights were also adjusted. It can be seen that from the “computer” values used in GreKo, they gradually converge to more classical values.
The following graph presents data related to another training session in which material weights were also adjusted. It can be seen that from the “computer” values used in GreKo, they gradually converge to more classical values.
We give a complete list of evaluation parameters with initial and final values. The meaning of the most part is clear without additional comments, those who wish to familiarize themselves with their exact purpose are invited to the source code of the program - the eval.cpp file, the Evaluate () function.
| room | Sign of | Description | Before training | After training |
|---|---|---|---|---|
| one. | VAL_P | pawn cost | 100 | 100 |
| 2 | VAL_N | horse cost | 400 | 400 |
| 3 | VAL_B | elephant cost | 400 | 400 |
| four. | VAL_R | rook cost | 600 | 600 |
| five. | Val_q | queen cost | 1200 | 1200 |
| 6 | Pawndoubled | double pawn | -ten | -ten |
| 7 | PawnIsolated | isolated pawn | -ten | -nineteen |
| eight. | Pawnbackback | backward pawn | -ten | -five |
| 9. | Pawncenter | pawn in the center of the board | ten | 9 |
| ten. | Pawnpassedfreemax | unblocked pass | 120 | 128 |
| eleven. | Pawnpassedblockedmax | locked gate | 100 | 101 |
| 12. | PawnPassedKingDist | distance from the opponent's king in the endgame | five | 9 |
| 13. | Pawnpassedsquare | checkpoint, unreachable by the "rule of the square" | 50 | 200 |
| 14. | KnightCenter | horse centralization | ten | 27 |
| 15. | KnightOutpost | protected item for a horse | ten | 7 |
| sixteen. | KnightMobility | horse mobility | 20 | nineteen |
| 17 | BishopPairMidgame | a pair of elephants in the middlegame | 20 | 20 |
| 18. | BishopPairEndgame | pair of elephants in the endgame | 100 | 95 |
| nineteen. | BishopCenter | elephant centralization | ten | 9 |
| 20. | BishopMobility | elephant mobility | 60 | 72 |
| 21. | Rook7th | rook on the 7th rank | 20 | 24 |
| 22 | Roookopen | an open rook | ten | 17 |
| 23. | Rookmobility | rook mobility | 40 | 40 |
| 24 | QueenKingTropism | the proximity of the queen to the opponent's king | 40 | 99 |
| 25 | KingCenterMid | centralization of the king in the middlegame | -40 | -41 |
| 26 | KingCenterEnd | centralization of the king in the endgame | 40 | 33 |
| 27. | KingPawnShield | king pawn shield | 120 | 120 |
The table shows an example for one of the training sessions, in which only the positional parameters of the evaluation were optimized, and the cost of the figures remained unchanged. This is not a critical requirement; in the tests described below, full training on all 27 parameters was used. But the best results in the practical game showed a version with a constant scale of material.
What conclusions can be drawn from the weights obtained? It can be seen that some of them have remained almost unchanged compared with the original version of the program. It can be assumed that over the years of debugging the engine, they were selected intuitively enough. However, at some points, cold mathematics amended human intuition. So, the damage of the backward pawns was overrated by the author. But the following parameters seemed more important to the algorithm, their weights were almost doubled:
- isolated pawn
- an open rook
- distance from the opponent's king in the endgame
- horse centralization
- the proximity of the queen to the opponent's king
We should also mention the sign of the checkpoint, which is unattainable according to the “rule of the square”. Its optimized value has reached the limit of the acceptable interval set by the algorithm. Obviously, it could be more. The reason, probably, is that in the training file, in the presence of such a passing pawn, the games were won 100% of the time. As a weight, the value of 200 was left as quite sufficient - its increase has practically no effect on the strength of the game.
Check at the chessboard
So, we have trained the evaluation function to predict the outcome of the game based on the position on the board. But the main test lies ahead - how much this skill will prove useful in a practical game. For this purpose, several versions of the engine with different settings were prepared, each of which was obtained in its own training mode.
| Version | Training file | Number of batches | Evaluation ratios | Scaling constant λ |
|---|---|---|---|---|
| A | 20000.pgn | 20,000 | 6 ... 27 | 40 |
| B | 20000.pgn | 20,000 | 1 ... 27 | 40 |
| C | 20000.pgn | 20,000 | 6 ... 27 | 20 |
| D | 20000.pgn | 20,000 | 1 ... 27 | 20 |
| E | 20000.pgn | 20,000 | 6 ... 27 | 60 |
| F | 20000.pgn | 20,000 | 1 ... 27 | 60 |
| G | gm2600.pgn | 27202 | 6 ... 27 | 20 |
| H1 | large.pgn | 47202 | 6 ... 27 | 20 |
| H2 | large.pgn | 47202 | 1 ... 27 | 20 |
20000.pgn - program parts with itself (superblits)
gm2600.pgn - grandmasters' games from the Crafty Robert Hyatt FTP site (classic control)
large.pgn - merge the two files
Each of the versions played 100 games with the original program GreKo 2015, as well as with a set of other engines with time control "1 second + 0.1 seconds per turn". The results are shown in the table below. With the help of the program bayeselo, relative ratings of versions were calculated, the power of GreKo 2015 was fixed as a reference point at the level of 2600. The value of LOS (likelihood of superiority) was also determined - the probability that a particular version plays stronger than GreKo 2015 taking into account the confidence interval of rating calculation.
| Version | GreKo 2015 | Fruit 2.1 | Delfi 5.4 | Crafty 23.4 | Kiwi 0.6d | Rating | LOS |
|---|---|---|---|---|---|---|---|
| GreKo 2015 | 33 | 40.5 | 39.5 | 73.5 | 2600 | ||
| A | 53.5 | 38 | 49.5 | 46.5 | 76 | 2637 | 97% |
| B | 55 | 43.5 | 71 | 36.5 | 78.5 | 2667 | 99% |
| C | 52.5 | 39.5 | 81 | 42.5 | 75 | 2672 | 99% |
| D | 42 | 23.5 | 58 | 33.5 | 68 | 2574 | 7% |
| E | 53.5 | 37 | 51.5 | 46 | 81.5 | 2646 | 99% |
| F | 59 | 36.5 | 63 | 31.5 | 79.5 | 2648 | 98% |
| G | 48 | 24.5 | 59 | 43.5 | 65.5 | 2602 | 54% |
| H1 | 45.5 | 40 | 51.5 | 40.5 | 75.5 | 2616 | 81% |
| H2 | 55 | 33.5 | 65 | 39 | 74 | 2646 | 99% |
It is seen that the improvement of the game occurred in all cases except one (version D). It is also interesting that training in the games of grandmasters (version G) had a slight effect. But the addition to the games of grandmasters of their own games of the program, plus the modification of the values of the pieces (version H2) turned out to be a fairly successful combination.
The strongest in the aggregate of results was version C, with an increase in the rating of about 70 points. For a given number of batches, this margin is statistically significant, the error is plus or minus 30 points.
We trained and tested the program at ultra-short time control, when one batch lasts a few seconds. Check how our improvements work in the "serious" game, with longer controls.
| Time control | Number of batches | Result | Rating | LOS |
|---|---|---|---|---|
| 1 minute. + 1 sec / move | 200 | 116.5 - 83.5 | + 56 | 99% |
| 3 min. + 2 seconds / move | 100 | 57.5 - 42.5 | + 45 | 94% |
| 5 minutes. on 40 moves | 100 | 53.5 - 46.5 | + 21 | 77% |
So, despite a slight drop in efficiency with an increase in the length of the games, the trained version definitely demonstrates a stronger game than the engine with the original settings. She was released as another final release of the program.
GreKo 2015 ML
The GreKo 2015 ML program can be freely downloaded along with the source code in C ++. It is a console application for Windows or Linux. To play with a person, analyze or spar with other engines, you may need a graphical interface - for example, Arena, Winboard, or some other. However, you can play directly from the command line, introducing moves using standard English notation.GreKo's self-learning function is implemented as a built-in command of the console mode (the author currently does not know other engines that support this functionality). The vector of 27 coefficients of the evaluation function is stored in the file weights.txt. To automatically adjust it based on a PGN file, you need to type the command learn, for example:
White(1): learn gm2600.pgn The program will read all batches from the specified file, create an intermediate file with training positions and break it into a training and test subset:
Creating file 'gm2600.fen' Games: 27202 Loading positions... Training set: 1269145 Validation set: 317155 It will then save the original values of the parameters to the weights.old file, and begin the optimization process. During operation, intermediate values of weights and target functionality are displayed on the screen and in the file learning.log.
Old values saved in file 'weights.old' Start optimization... 0 0.139618890118 0.140022159883 2016-07-21 17:01:16 Parameter 6 of 27: PawnDoubled = -10 Parameter 7 of 27: PawnIsolated = -19 1 0.139602240177 0.140008376153 2016-07-21 17:01:50 [1.7] -20 2 0.139585446564 0.139992945184 2016-07-21 17:01:58 [1.7] -21 3 0.139571113698 0.139980624436 2016-07-21 17:02:07 [1.7] -22 4 0.139559690029 0.139971803640 2016-07-21 17:02:15 [1.7] -23 5 0.139552067028 0.139965861844 2016-07-21 17:02:23 [1.7] -24 6 0.139547879916 0.139964477620 2016-07-21 17:02:32 [1.7] -25 7 0.139543242843 0.139961056939 2016-07-21 17:02:40 [1.7] -26 8 0.139542575174 0.139962314286 2016-07-21 17:02:48 [1.7] -27 Parameter 8 of 27: PawnBackwards = -5 9 0.139531995624 0.139953185941 2016-07-21 17:03:04 [1.8] -4 10 0.139523642489 0.139947035972 2016-07-21 17:03:12 [1.8] -3 11 0.139518695795 0.139943580937 2016-07-21 17:03:21 [1.8] -2 12 0.139517501456 0.139943802704 2016-07-21 17:03:29 [1.8] -1 Parameter 9 of 27: PawnCenter = 9 Parameter 10 of 27: PawnPassedFreeMax = 128 13 0.139515067927 0.139941456600 2016-07-21 17:04:00 [1.10] 129 14 0.139500815202 0.139927669884 2016-07-21 17:04:08 [1.10] 130 ... Upon completion of the training, the weights.txt file will contain the new values of the weights, which will take effect the next time the program is launched.
The learn command can contain two more arguments, the lower and upper bounds of the optimization interval. By default, they are 6 and 27 - i.e. all signs, except the cost of figures, are optimized. To enable full optimization, you must specify the boundaries explicitly:
White(1): learn gm2600.pgn 1 27 The algorithm is randomized (in terms of splitting into training and test samples), therefore, for different starts unequal vectors of coefficients can be obtained.
findings
To configure the evaluation function, we used self-learning program (reinforcement learning). The best results were achieved by analyzing the games of the program against itself. In fact, the only external source of chess knowledge was the opening book of the shell, necessary for the randomization of the games played.
We were able to increase the predictive ability of the assessment, which led to a statistically significant increase in the strength of the game at different time controls, both with the previous version and with a set of independent opponents. The improvement was 50 ... 70 points Elo.
It is worth noting that the result was achieved in fairly modest volumes: about 20 thousand parties and 1 million positions (for comparison: AlphaGo studied on 30 million positions from parties of strong amateurs from the server, not counting further games with herself). The evaluation function of GreKo is also very simple, and includes only 27 independent parameters. In the strongest chess engines, their score can go on hundreds and thousands. However, even in such an environment, machine learning methods led to success.
Further improvement of the program could include adding new criteria to the evaluation function (in particular, taking into account the stage of the game for all the considered parameters) and using more advanced methods of multidimensional optimization (for example, searching for global extremes). At the moment, however, the author’s plans in this direction have not yet been determined.
Links
- Determine the weight of chess pieces by regression analysis - an introductory article on the material evaluation model.
- GreKo is the GreKo chess program, which we were engaged in in this article.
- Texel's Tuning Method - a description of the basic method for optimizing the evaluation function.
- Mastering the Game of the Deep Neural Networks and Tree Search (English) - an original article on AlphaGo in Nature.
- AlphaGo on fingers - a statement of the basic principles of the AlphaGo device in Russian.
- Giraffe: Using Deep Reinforcement Learning to Play Chess (English) - An article about the Giraffe chess program.
- bayeselo is a utility for calculating ratings based on PGN files.
Source: https://habr.com/ru/post/305604/
All Articles