Functors (chapter of the book "Category Theory for Programmers")

This is the seventh article from the series "Theory of Categories for Programmers." Previous articles have already been published on Habré:

Functors

There is a very simple but powerful idea behind the notion of a functor (no matter how bad it sounds). Just the theory of categories is full of simple and powerful ideas. A functor is a mapping between categories. Let two categories C and D be given, and the functor F maps objects from C to objects from D — this is a function above the objects. If a is an object from C, then we will denote its image from D as F a (without parentheses). But a category is not only objects, but also morphisms connecting them. The functor also displays morphisms - this is a function over morphisms. But morphisms are not displayed as horrible, but in order to maintain connections. Namely, if the morphism f of C binds the object a with the object b ,

f :: a -> b

then the image of f in D, F f , connects the image of a with the image of b :

 F f :: F a -> F b

(We hope that such a mixture of mathematical notation and Haskell syntax is understandable to the reader. We will not write brackets when applying functors to objects or morphisms.)

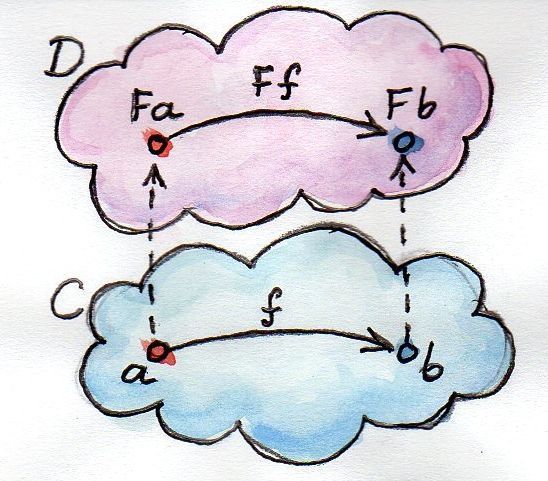
As you can see, the functor preserves the structure: what was connected in the input category will be connected in the output. But this structure is not exhausted: it is also necessary to support the composition of morphisms. If h is a composition of f and g :

then we require that its image under the action of F be the composition of the images of f and g :

 F h = F g . F f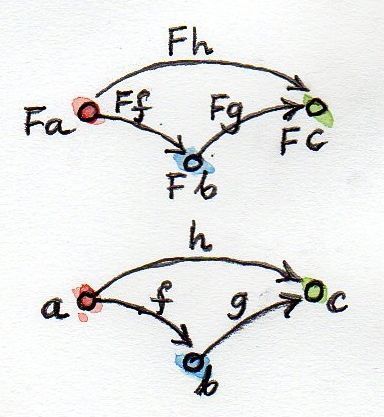

Finally, we require that all single (identical) morphisms from C be mapped to single morphisms from D:

 F id(a) = id(F a)

Here id _a is the unit morphism of object a , and id _{F a} is the unit morphism of object F a .

Note that all these conditions significantly limit the range of functions suitable as morphisms. Functors must preserve the structure of a category. If we imagine a category as a set of objects intertwined with morphisms, then the functor has no right to tear off any thread of this lace. It can combine several objects, it can glue morphisms into one, but it never breaks ties. This limitation is analogous to the concept of continuity from mathematical analysis. In this sense, functors are "continuous" (although there is an even more restrictive definition of the continuity of functors). Like any function, a functor can be both gluing and nesting. The nesting aspect is most pronounced when the source category is much smaller than the target. In the limiting case, the initial category is a category 1 , consisting of one object and one (single) morphism. A functor from category 1 to any other category simply selects a particular object from this category. There is a complete analogy with singleton morphisms that select elements from target sets. The gluing aspect, reduced to the point of absurdity, is observed in the constant functor Δ _c . It maps each object of the source category to a specific object c of the target category, and any morphism into a single morphism id _c . It's like a black hole sucking everything at a singularity point. We will return to the consideration of this functor when discussing limits and values.

Functors in programming

Let's go back to earth, to the world of programming. So, we have a category of types and functions. Consider functors that map this category into themselves — the so-called endofunctors. What is the endofunctor in the type category? First of all, it compares one type with another. Such mappings are in fact familiar to us; they are types that are parameterized by other types. Consider a few examples.

Maybe Functor

The definition of Maybe is a mapping of type a to type Maybe a:

 data Maybe a = Nothing | Just a

An important detail: Maybe by itself is not a type, but a type constructor . It takes a type, such as Int or Bool , as an argument, and returns a different type. Maybe without arguments is a function on types. But is Maybe functor? (Hereinafter, speaking of functors in the context of programming, endofunctors are almost always meant.) After all, a functor is not only a representation of objects (here, types), but also a display of morphisms (here, functions). For any function from a to b

 f :: a -> b

I would like to get a function from Maybe a to Maybe b . To determine such a function, you need to consider two cases corresponding to the two Maybe constructors. In the case of Nothing we simply return Nothing back. If the argument is Just , then apply the function f to its contents. So, the image of f under the action of Maybe is a function

 f' :: Maybe a -> Maybe b f' Nothing = Nothing f' (Just x) = Just (fx)

(By the way, in Haskell it is allowed to use apostrophes in variable names, which is very convenient in such cases.) In Haskell, the appearance of a functor responsible for the display of morphisms is implemented by a higher-order fmap . For Maybe it has the following signature:

 fmap :: (a -> b) -> (Maybe a -> Maybe b)

It is often said that fmap elevates (lifts) the function. Sublime function works on Maybe values. As usual, due to currying, this signature can be interpreted in two ways: either as a function of one variable, which is itself a function (a->b) , which returns a function (Maybe a -> Maybe b) , or as a function of two variables, which returns Maybe b :

 fmap :: (a -> b) -> Maybe a -> Maybe b

Following the above, we give the definition of fmap for Maybe :

 fmap _ Nothing = Nothing fmap f (Just x) = Just (fx)

To show that the Maybe type constructor together with the function fmap make up the functor, it remains to prove that fmap preserves single morphisms and composition. These statements are called "functorial laws", but they simply certify the preservation of the structure of the category.

Equivalent Transformation Method

We prove functorial laws by the method of equivalent transformations , which is a typical technique of proofs in Haskell. The method relies on the fact that functions in Haskell are defined by a set of equalities: the left side is equal to the right, both of them can be substituted for each other (it is possible that you need to rename variables during substitution to avoid conflicts). You can either substitute the body of the function instead of calling it (inline), or calling the function instead of its body (refactoring). Consider as an example the identical function:

 id x = x

If we meet somewhere, say id y , then it can always be replaced by y (inline). In general, any occurrence of id applied to an expression, for example, id (y + 2) , can be replaced by the expression itself (y + 2) . In the opposite direction: any expression e can be replaced by id e (refactoring). In the case of functions defined by pattern matching, each definition can be used independently. For example, according to the above definition of fmap you can replace fmap f Nothing with Nothing or vice versa. Consider this approach in practice. Let's start with the preservation of identity:

 fmap id = id

Two cases should be considered: Nothing and Just . Let's start with Nothing (I describe the transformation of the left side of the equality to the right side using pseudo-Haskell):

  fmap id Nothing = {   fmap } Nothing = {   id } id Nothing

Notice that in the second step we substituted id Nothing instead of Nothing , using the id definition in the opposite direction. In practice, such proofs are made by the method of “igniting the wick from two ends,” up to a meeting in the middle on the same expression, Nothing in this case. The second case is also simple:

  fmap id (Just x) = {   fmap } Just (id x) = {   id } Just x = {   id } id (Just x)

Now we will show that fmap saves the composition:

 fmap (g . f) = fmap g . fmap f

Let's start with the case of Nothing :

  fmap (g . f) Nothing = {   fmap } Nothing = {   fmap } fmap g Nothing = {   fmap } fmap g (fmap f Nothing)

Now it's time to Just :

  fmap (g . f) (Just x) = {   fmap } Just ((g . f) x) = {    } Just (g (fx)) = {   fmap } fmap g (Just (fx)) = {   fmap } fmap g (fmap f (Just x)) = {    } (fmap g . fmap f) (Just x)

It is worth emphasizing that for functions with side effects in the C ++ style, the equivalent transformation method does not work. Consider an example:

 int square(int x) { return x * x; } int counter() { static int c = 0; return c++; } double y = square(counter());

The equivalent transformation method would allow square to be expanded and get

 double y = counter() * counter();

Definitely, such a transformation is incorrect and changes the result of the expression. Despite this, if you define square as a macro, the C ++ preprocessor will use the equivalent transformation method with a catastrophic result.

Maybe again

Functors are easily expressed in Haskell, but they can be described in any language that supports generic programming and higher-order functions. Consider the C ++ analogue Maybe, the template type is optional . Here is a sketch of the implementation (the full implementation is much more complicated, since it explicitly describes different ways of passing arguments, copying semantics and other issues specific to C ++ resource management):

 template<class T> class optional { bool _isValid; // the tag T _v; public: optional() : _isValid(false) {} // Nothing optional(T x) : _isValid(true) , _v(x) {} // Just bool isValid() const { return _isValid; } T val() const { return _v; } };

The above pattern provides half the functor description: a type mapping. It maps the new type optional<T> each type T Now we describe its action on the functions:

 template<class A, class B> std::function<optional<B>(optional<A>)> fmap(std::function<B(A)> f) { return [f](optional<A> opt) { if (!opt.isValid()) return optional<B>{}; else return optional<B>{ f(opt.val()) }; }; }

This is a higher order function that takes a function as an argument and returns a function. And here is another option, without currying:

 template<class A, class B> optional<B> fmap(std::function<B(A)> f, optional<A> opt) { if (!opt.isValid()) return optional<B>{}; else return optional<B>{ f(opt.val()) }; }

On the other hand, fmap can be implemented as the optional template method. Such ambiguity in the choice makes the abstraction of the pattern "functor" in C ++ a problem. Should the functor be an interface in order to be inherited from it (unfortunately, the template functions cannot be virtual)? Or maybe a free template function, curried or not? Can the C ++ compiler correctly infer the missing types, or should they be specified explicitly? Imagine that the input function f converts an int into a bool . How the compiler will determine the g type:

 auto g = fmap(f);

especially if in the future there will be a lot of functors with their versions of fmap ? (We will get acquainted with other kinds of functors soon.)

Type Classes

How is the functor abstraction implemented in Haskell? The type class mechanism is used. A type class defines a family of types that support a single interface. For example, the class of objects comparable to equality is defined as:

 class Eq a where (==) :: a -> a -> Bool

Here it is stated that type a belongs to class Eq if it supports the operator (==) , which takes two arguments of type a and returns Bool . To convince Haskell that a particular type belongs to Eq , you need to declare it an instance (instance, implementation) of a class, and provide an implementation (==) . For example, having the following definition of a point on a plane (type-product of two Float ):

 data Point = Pt Float Float

You can determine the equality of points:

 instance Eq Point where (Pt xy) == (Pt x' y') = x == x' && y == y'

Here the defined operator (==) is located infixno, between two samples (Pt xy) and (Pt x' y') . The body of the function is placed to the right of the = sign. After Point declared as an instance of Eq , you can directly compare points for equality. Note that, unlike C ++ or Java, you are not required to provide a class or even an Eq interface at the time the Point defined — this can be done later. Note that type classes are the only mechanism for overloading functions (and operators) in Haskell. We will need it to overload fmap for different functors. There is one subtlety: a functor is defined not as a type, but as a function over types, a type constructor. Our type class should describe a family of type constructors, not just types, as was the case with Eq . Fortunately, the Haskell type class mechanism works with type constructors as well as with simple types ( PP: a good example of following a functional paradigm — even in the world of function types is no worse than objects ). The following is the definition of the Functor class:

 class Functor f where fmap :: (a -> b) -> fa -> fb

It states that f is a Functor if there is a function fmap with this signature. Here f - t and new variable are of the same kind as m and new variables a and b . But the compiler is able to understand that f is a type constructor, tracking its use: applying to other types, here fa and fb . Accordingly, it is the type constructor that we declare as an instance of the functor, as in the case of Maybe:

 instance Functor Maybe where fmap _ Nothing = Nothing fmap f (Just x) = Just (fx)

I note that the class Functor , as well as declarations of many commonly used types, including Maybe its instances, are included in the standard Prelude library.

Functors in C ++

Can we apply the same approach in C ++? The type constructor corresponds to a template class, such as optional , respectively, we need to parameterize fmap twice with the template parameter F This is written like this:

 template<template<class> F, class A, class B> F<B> fmap(std::function<B(A)>, F<A>);

But how do we specialize this template for different functors? Unfortunately, partial specialization of C ++ template functions is prohibited. You can not write:

 template<class A, class B> optional<B> fmap<optional>(std::function<B(A)> f, optional<A> opt)

Instead, we have to return to overloading the functions, as a result we return to the original definition of fmap (without currying):

 template<class A, class B> optional<B> fmap(std::function<B(A)> f, optional<A> opt) { if (!opt.isValid()) return optional<B>{}; else return optional<B>{ f(opt.val()) }; }

This definition works, but a second argument is required for proper overload. The more general definition of fmap simply ignored.

List functor

For a better understanding of the importance of functors in programming, more examples are worth considering. Any type that is parameterized by another type is a candidate for the role of a functor. For example, generic containers are parameterized by the type of their elements, consider a list, a very simple container:

 data List a = Nil | Cons a (List a)

Here we have a List type constructor representing a mapping of any type a to type List a . To show that List is a functor, we need to define the lifting of functions along the functor. For a given function a->b we define List a -> List b :

 fmap :: (a -> b) -> (List a -> List b)

The function acting on the List should consider two cases, according to the two list constructors. The case of Nil is trivial, - and Nil is returned, you cannot squeeze much from the empty list. Cons trickier because it affects recursion. Let's think: so, we have a list a , a function f turns a into b , and we want to get a list b . Obviously, you need to use f to convert each list item from a to b . What exactly needs to be done if our (non-empty) list is defined as Cons head and tail? Apply f to the head and apply the raised (fmap) f to the tail. This definition is recursive, we define raised f through raised f :

 fmap f (Cons xt) = Cons (fx) (fmap ft)

It is important that on the right side fmap f is applied to the list shorter than what we define - namely, to the tail of the latter. We apply recursion to increasingly shorter lists, so we inevitably arrive at an empty list, or Nil . But as we have already defined, fmap f from Nil gives Nil , thus completing the recursion. The final result is obtained by combining a new head ( fx ) with a new tail ( fmap ft ) using the Cons constructor. As a result, here’s our declaration of the list as an instance of a functor completely:

 instance Functor List where fmap _ Nil = Nil fmap f (Cons xt) = Cons (fx) (fmap ft)

If you are used to C ++, it makes sense to consider std::vector , in fact, the basic C ++ container. The fmap implementation for std::vector is just a wrapper around std::transform :

 template<class A, class B> std::vector<B> fmap(std::function<B(A)> f, std::vector<A> v) { std::vector<B> w; std::transform( std::begin(v) , std::end(v) , std::back_inserter(w) , f); return w; }

With its help, we can, for example, square a row of numbers:

 std::vector<int> v{ 1, 2, 3, 4 }; auto w = fmap([](int i) { return i*i; }, v); std::copy( std::begin(w) , std::end(w) , std::ostream_iterator(std::cout, ", "));

Most C ++ containers are essentially functors. This is ensured by the presence of iterators that can be passed to std::transform , to a primitive relative of fmap . Unfortunately, the simplicity of the functor is lost under the rubbish of iterators and temporal variables (as in the fmap implementation above). From the good news, the planned (planned) for inclusion in C ++ library of intervals (ranges) significantly reveals them, intervals, functional nature.

Reader functor

Now that we have developed some kind of intuition, in particular that functors are containers of a kind, here is an example that looks completely different at first glance. Consider a mapping of type a onto the type of functions returning a . We have not yet reached the discussion of functional types at the proper category-theoretic level, but we, as programmers, have a certain understanding of them. In Haskell, functional types are constructed using a type constructor — an arrow (->) , which takes two types: the type of the argument and the type of the result. You have already met it in the infix notation, a->b , but with the help of parentheses, you can use the prefix notation just as well:

 (->) ab

As well as usual functions, m and new functions of several arguments can be applied partially. And when we give the arrow one argument, it is still waiting for another. I.e,

 (->) a

is a type constructor; we need another type b to make a full type a->b . Thus, the arrow defines a whole family of type constructors parameterized a . Let's find out if it is also a family of functors. Not to confuse the two parameters, rename them, emphasizing the role. In accordance with our previous definitions of functors, the type of the argument is called r , and the type of the result is a . So, our constructor takes any type a , and maps it to type r->a . To justify functoriality, we need to raise the function a->b to a function that accepts r->a and returns r->b . These are the types created by the constructor action (->) r on a and b respectively. This is the signature of fmap :

 fmap :: (a -> b) -> (r -> a) -> (r -> b)

We get a kind of puzzle: having functions f::a->b and functions g::r->a , create r->b . There is only one way to compose them, and the result is just what we need. fmap :

 instance Functor ((->) r) where fmap fg = f . g

It worked! , :

 fmap fg = (.) fg

, :

 fmap = (.)

(->) r fmap "reader".

, , - , . reader , . , , . . , Haskell , . , , , :

 nats :: [Integer] nats = [1..]

, — Haskell . . , . , Integer - . Haskell : , , . , , , . strlen , . , . , , , , ! ( ) ( ), . C++, — std::future , - , ; , , , . IO Haskell, , “Hello World!” . , , , . . , , — . , — . , — , , , , . , , , a :

 data Const ca = Const c

Const , c a . , , , (->) .

 fmap :: (a -> b) -> Const ca -> Const cb

, fmap , — :

 instance Functor (Const c) where fmap _ (Const v) = Const v

C++ ( , !), , , , .

 template<class C, class A> struct Const { Const(C v) : _v(v) {} C _v; };

C++ - fmap , Const , .

 template<class C, class A, class B> Const<C, B> fmap(std::function<B(A)> f, Const<C, A> c) { return Const<C, B>{c._v}; }

, Const . Δ _c , — . .

, , . , , , . , , . Nothing special. , . maybeTail ( : )? , Haskell:

 maybeTail :: [a] -> Maybe [a] maybeTail [] = Nothing maybeTail (x:xs) = Just xs

( , Nil [] . Cons : ().) maybeTail , Maybe [] , a . fmap , f : Maybe list ? . fmap , Maybe . f Maybe , f . ( fmap f ), . , Maybe list :

 square x = x * x mis :: Maybe [Int] mis = Just [1, 2, 3] mis2 = fmap (fmap square) mis

, , fmap Maybe , , — list . , , :

 mis2 = (fmap . fmap) square mis

, fmap :

 fmap :: (a -> b) -> (fa -> fb)

, fmap (fmap . fmap)

 square :: Int -> Int

 [Int] -> [Int]

fmap

 Maybe [Int] -> Maybe [Int]

mis . , , fmap fmap . : , ( , ). , , , . , . ? , , . . , , . , Cat ( , ). "" , , -, , . , "". , , , . , .

`Maybe` ,
fmap _ _ = Nothing
? (: )
`reader` (: ).
reader (, , Haskell).
. , ( ).

Thanks

. .
leshabirukov : Bodigrim , . .

Source: https://habr.com/ru/post/305018/

All Articles