Factor modeling based on the Verlet method
The Verle Method is an iterative method for calculating the next location of a material point from the current and past locations, taking into account the overlaid relationships within the system of points.
Elastic structure is the most common type of structure for approximating data. This is a set of knots and elastic connections between them. As such connections there may be a spring connection between a pair of points with an equilibrium distance between points and ribs of three nodes with an equilibrium angle between the nodes. To approximate a set of points by an elastic structure, it is proposed to use the physical interpretation of data points as centers attracting nodes of an elastic structure. A special case of an elastic structure is the nonlinear principal components. This is a set of elastic chains with a common point of intersection. With a high stiffness of elastic bonds, the nonlinear principal components transform into the classical principal components of factor analysis. To calculate the motion of points of an elastic structure in the field of attraction and taking into account the connections between the nodes of the elastic structure, it is proposed to use the Verlet numerical integration method.
The multidimensional scaling allows, within the framework of the hypothesis of the dimension of the target space, to arrange objects according to their mutual distances so that the reconstructed distances between the objects approach the empirical ones. Based on the Verlet method, it is proposed to carry out multidimensional scaling, thus the mutual distances between points will be taken into account with the greatest accuracy. The correlation matrix will act as a matrix of mutual distances. With the help of multidimensional scaling, the factorization of the correlation matrix will be implemented, thereby the factor structure of the data in the factor space will be restored. To obtain an interpretable solution, it is proposed to use separate methods of factor rotation applied to the recovered factor structure.
The Verlet algorithm is used to calculate the following position of the point on the current and past:
')
 ,
,
 - the calculated coordinates of the j -th point at the i -th iteration,
- the calculated coordinates of the j -th point at the i -th iteration,
m is the dimension of space
 Is the velocity vector of the jth point.
Is the velocity vector of the jth point.
 - the influence vector of the k- th center of attraction represented by the data point
- the influence vector of the k- th center of attraction represented by the data point  on the jth point
on the jth point
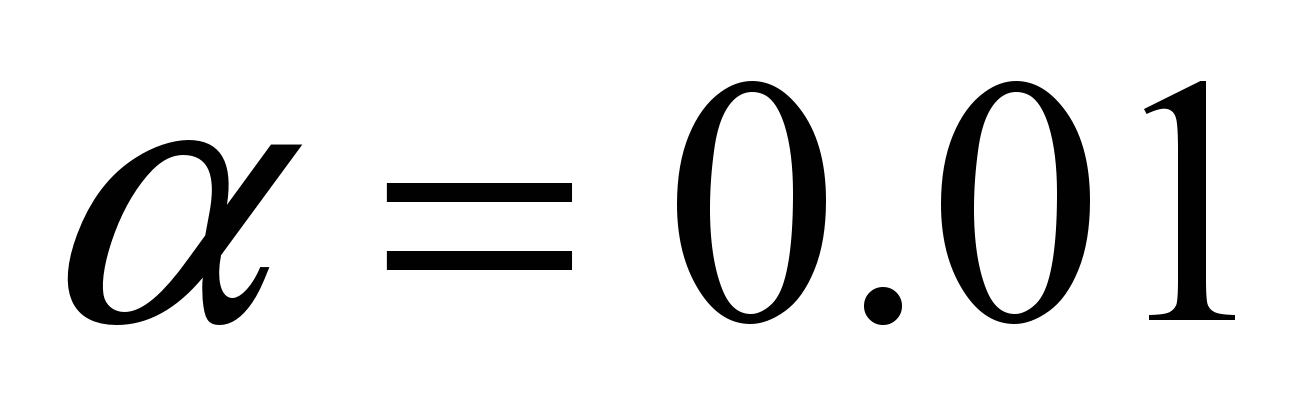 .
.
Restrictions are imposed on the system of points: some of the points are connected by elastic rods of a given length.
The algorithm works as follows:
For example, s = 16.
The procedure for relaxation of communication is described by the following formulas:
If the link is represented by dots and
and  with equilibrium distance between them
with equilibrium distance between them  then
then
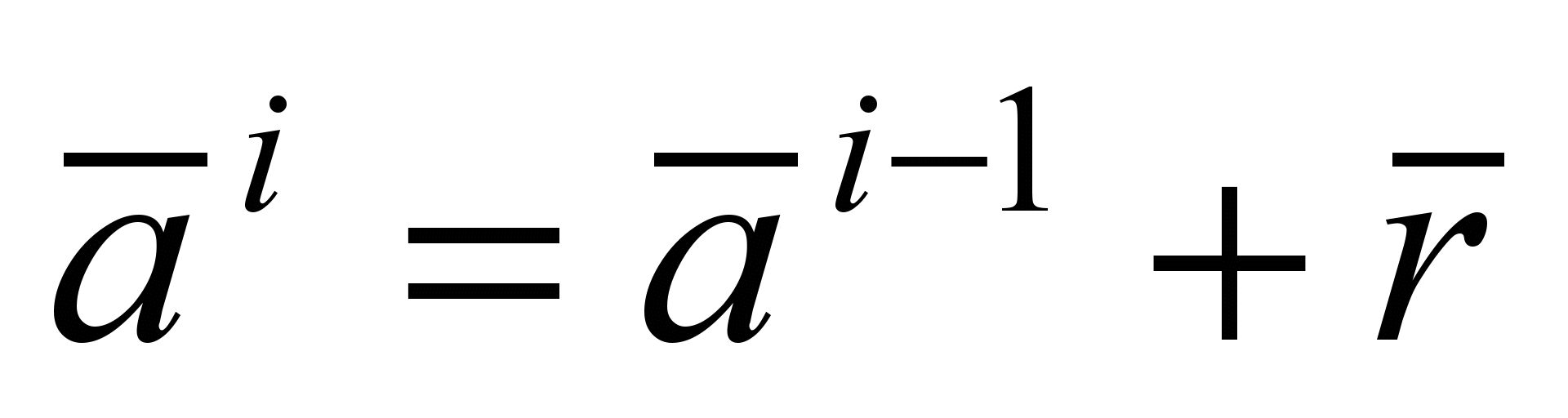 ,
,
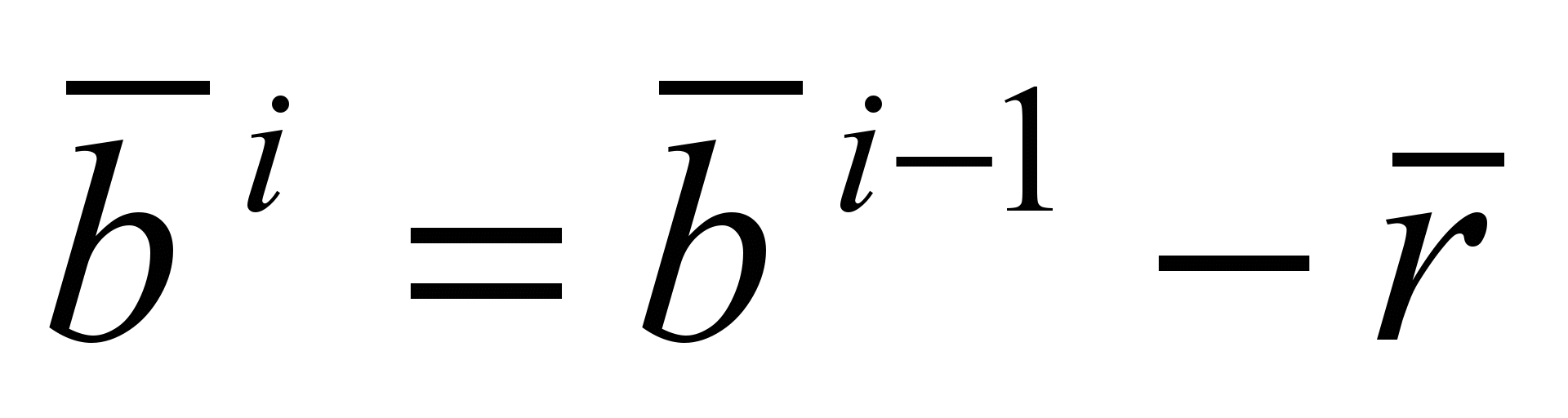 ,
,
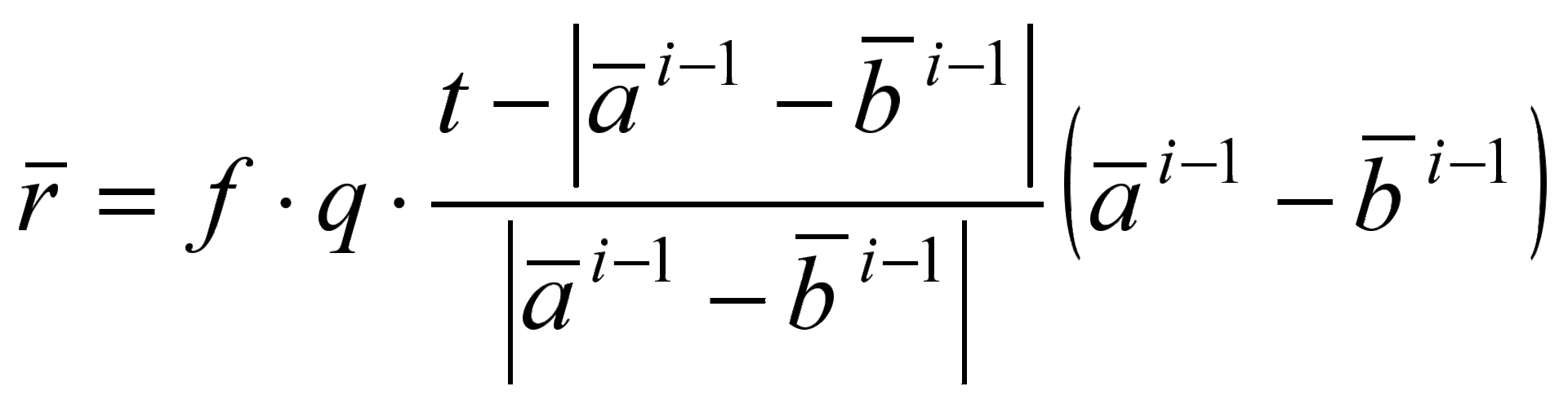 ,
,
 - coefficient of elasticity of communication,
- coefficient of elasticity of communication,
 - coefficient depending on the number s of repetitions of step 2.
- coefficient depending on the number s of repetitions of step 2.

Fig. 1. Spring connection of a pair of points with an equilibrium distance
Triplets of knots can form stiffening ribs with an equilibrium angle. Such connections are proposed to be emulated by connections in the form of elastic rods between the extreme points. The equilibrium distance between the extreme points in this case is determined from the equality of the triangle. If the link is represented by dots ,
,  ,
,  equilibrium angle
equilibrium angle 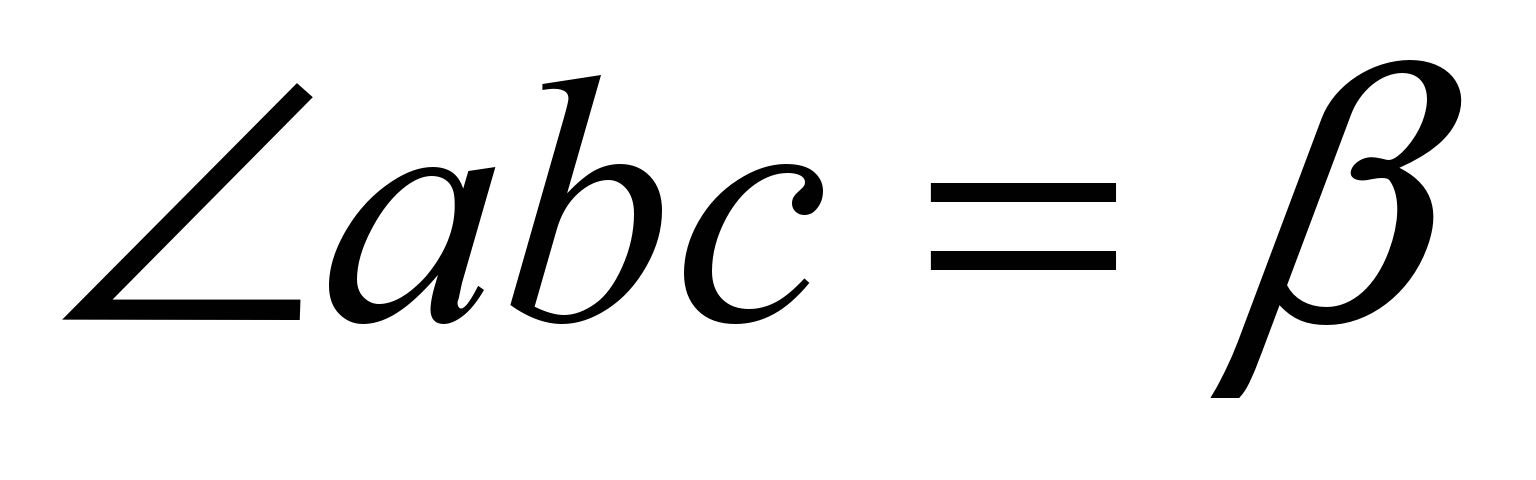 then equilibrium distance
then equilibrium distance  between points and is calculated by the formula:
between points and is calculated by the formula:
 .
.

Fig. 2. Stiffener of three points with an equilibrium angle
Multidimensional scaling (MNSH) is a way of the most effective placement of objects, approximately keeping the distances observed between them. MNS places objects in a space of a given dimension and checks how accurately the resulting configuration maintains the distance between objects. MNSH uses the minimization algorithm for a certain function that evaluates the quality of the resulting display options.
The measure most commonly used to assess the quality of the fit model (mapping), measured by the degree of reproduction of the original matrix of similarities, is the so-called stress. The magnitude of the stress φ for the current configuration is defined as:
 .
.
Here d ij are the reproduced distances in the space of a given dimension, and
δ ij is the initial distance.
m is the number of objects.
The function f (δ ij ) denotes a non-metric monotone transformation of the original data (distances). The MNSH does not reproduce the quantitative measures of the similarities of objects, but only their relative order. The smaller the stress value, the better the matrix of initial distances is consistent with the matrix of resulting distances.
The main component model is described by the following formulas:
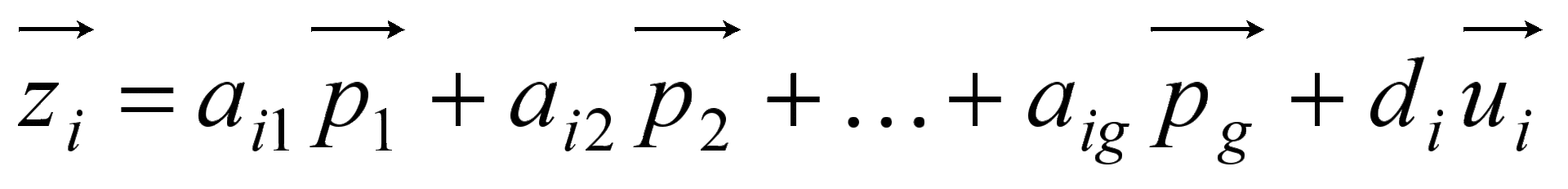
m is the number of variables
g - the number of factors
 - source variables
- source variables
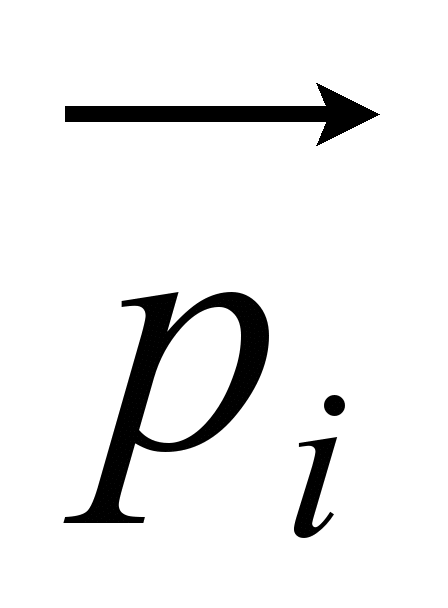 - common factors
- common factors
 - specific factors.
- specific factors.
As a system of points for the Verlet method, the coordinate system represented by the axes can be used ,
,
 where
where
w is the number of points forming the factor axis,
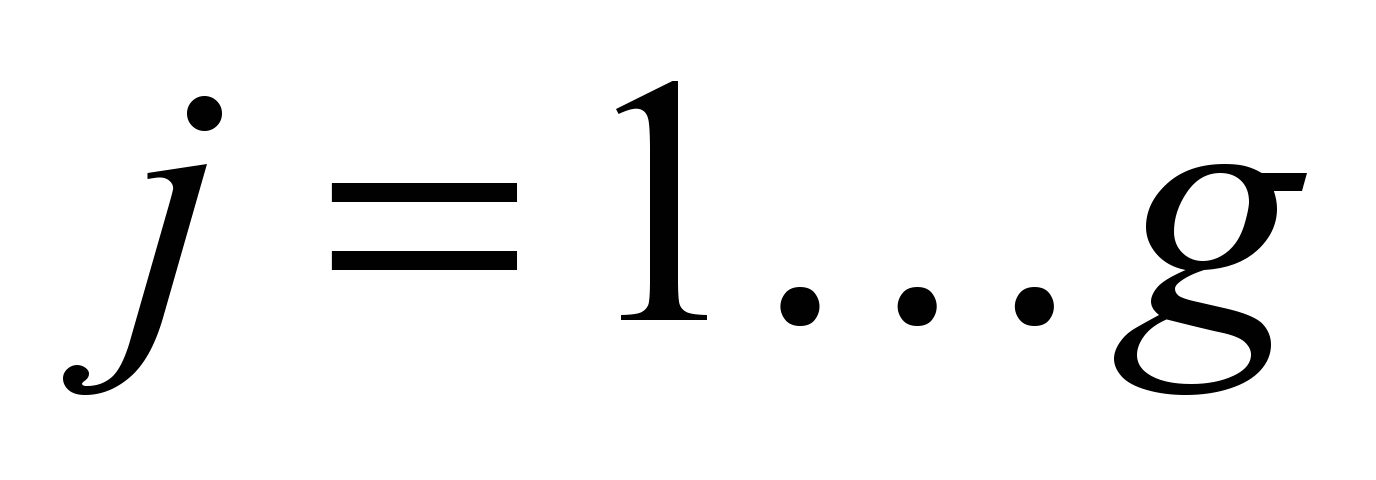 ,
,
g is the number of factor axes.
For example, when (number w must be odd large 1)
(number w must be odd large 1)

l is the distance between a pair of neighboring points forming the factor axis.
 - index of the center point of the factor axis.
- index of the center point of the factor axis.
Pairs of points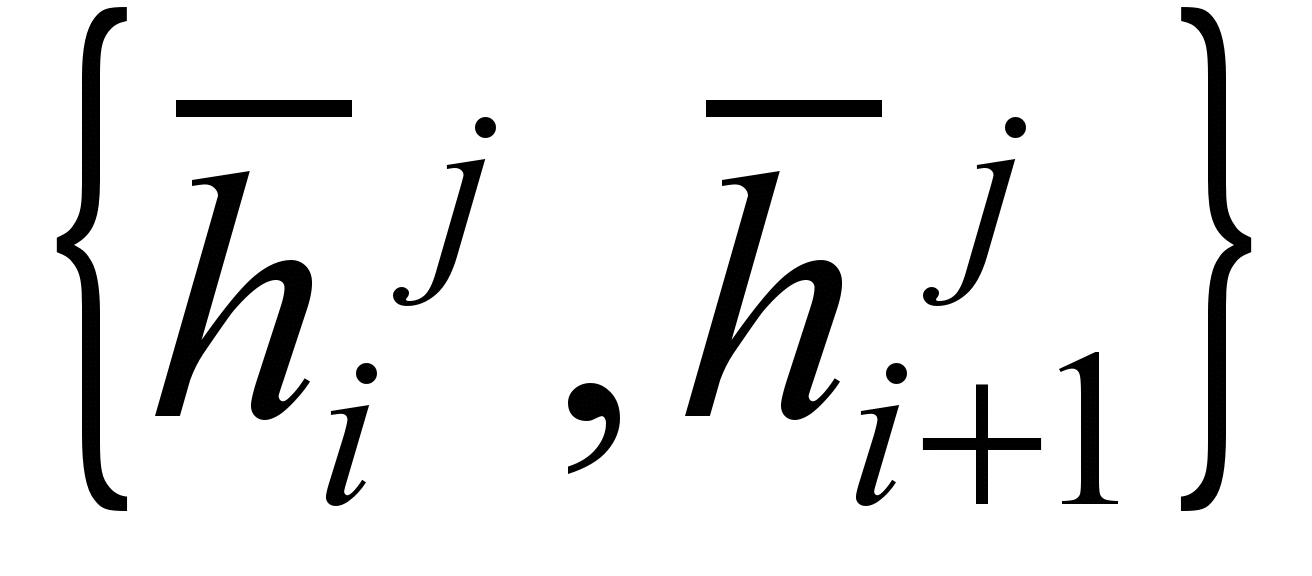 form a connection with the equilibrium distance l .
form a connection with the equilibrium distance l .
Pairs of points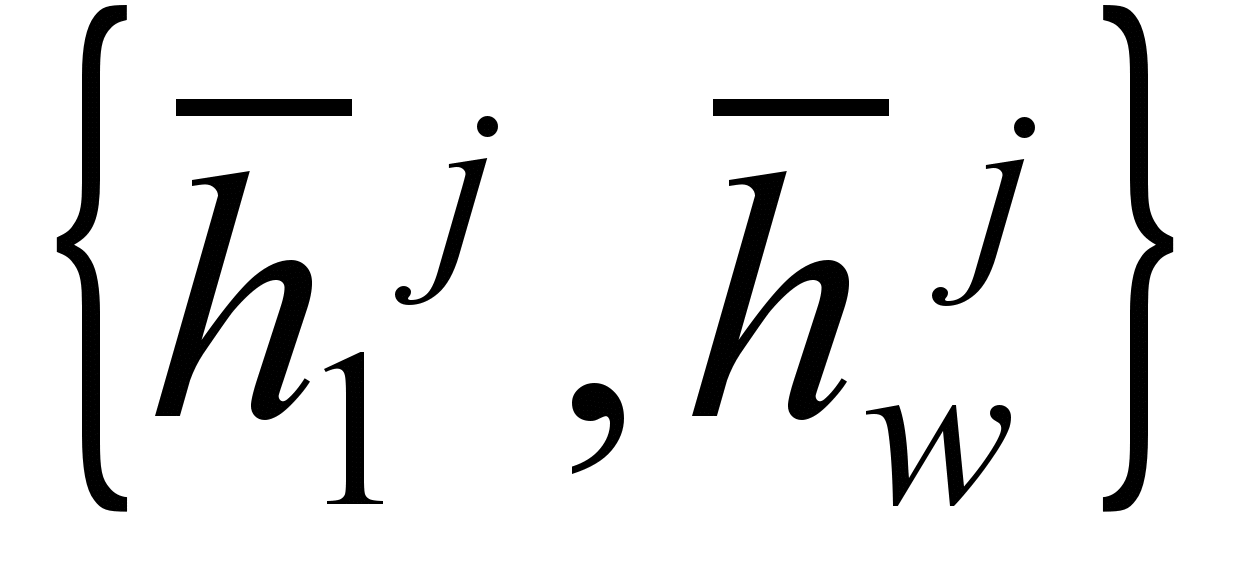 form a connection with the equilibrium distance
form a connection with the equilibrium distance 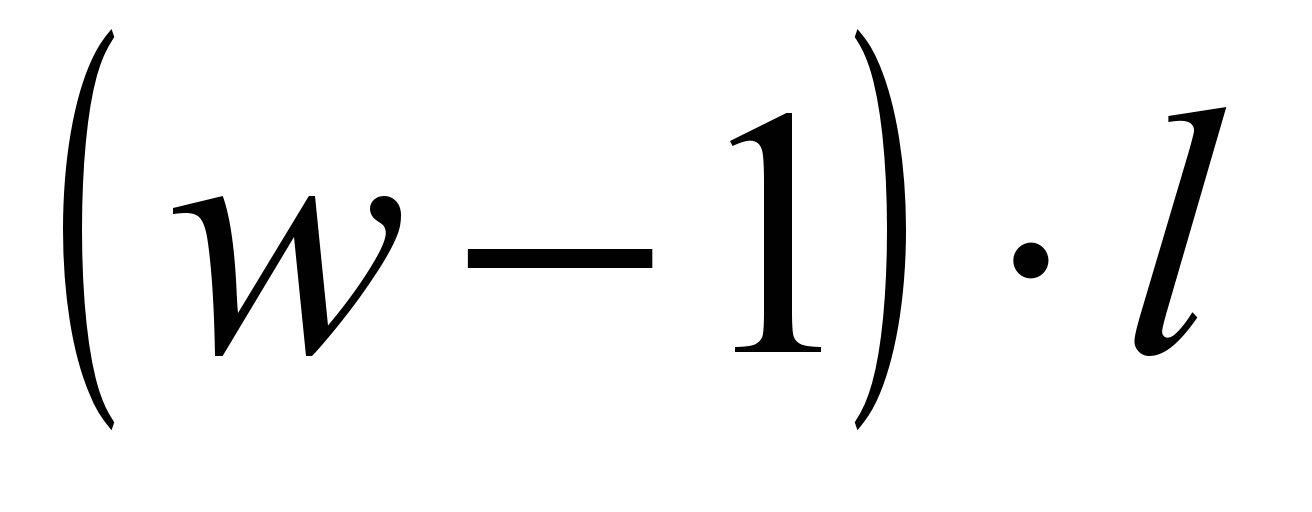 .
.
All pairs of points different axes i and j form a connection with a zero equilibrium distance.
different axes i and j form a connection with a zero equilibrium distance.
Pairs of points ,
,  ,
, 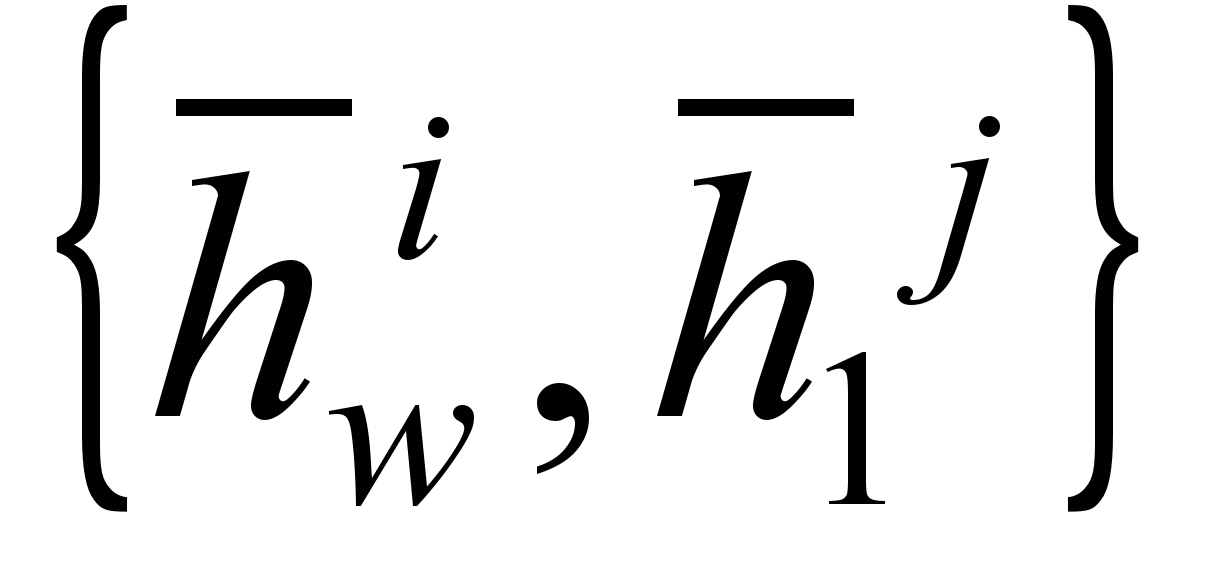 ,
, 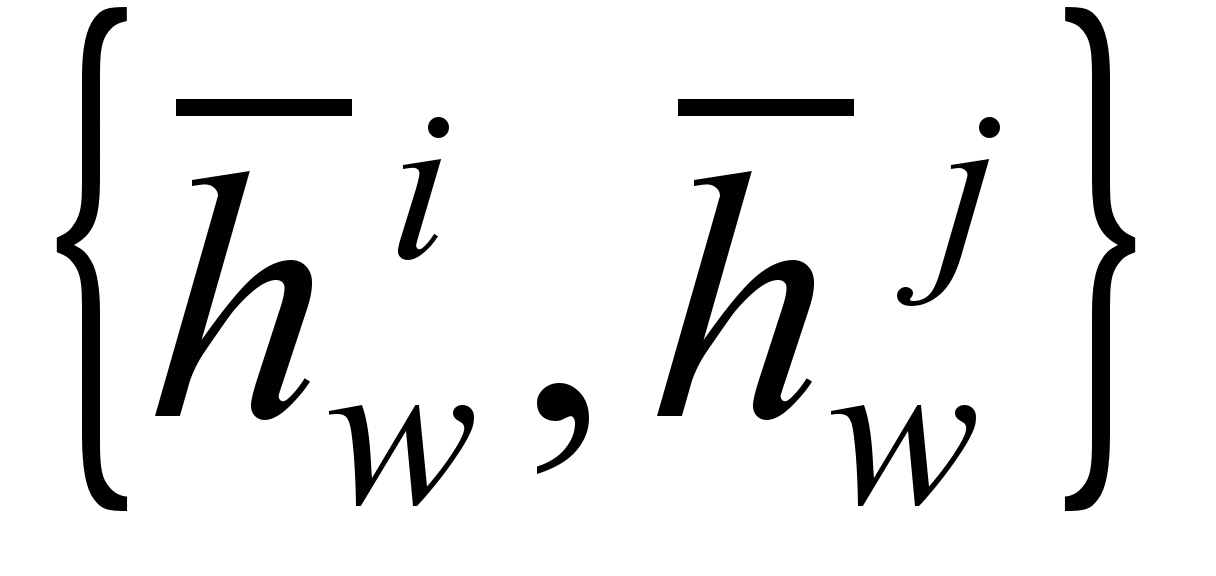 different axes i and j form a connection with an equilibrium distance equal to the initial distance between the points. These relationships define right angles between the various factor axes i and j . Another way to specify an orthogonal factor structure is to add stiffeners with a right equilibrium angle between triples of points.
different axes i and j form a connection with an equilibrium distance equal to the initial distance between the points. These relationships define right angles between the various factor axes i and j . Another way to specify an orthogonal factor structure is to add stiffeners with a right equilibrium angle between triples of points.  between different factor axes i and j .
between different factor axes i and j .


Fig. 3. Ways to set the factor structure for the Verlet method
Elements of the factor structure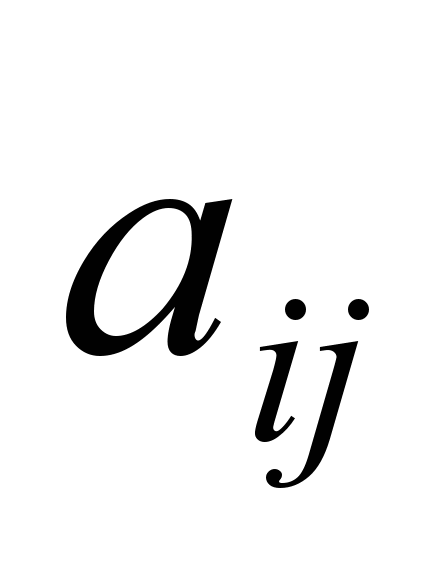 can be defined as the correlation coefficient between the j -th factor axis and the i -th axis of the original coordinate system:
can be defined as the correlation coefficient between the j -th factor axis and the i -th axis of the original coordinate system:
 ,
,
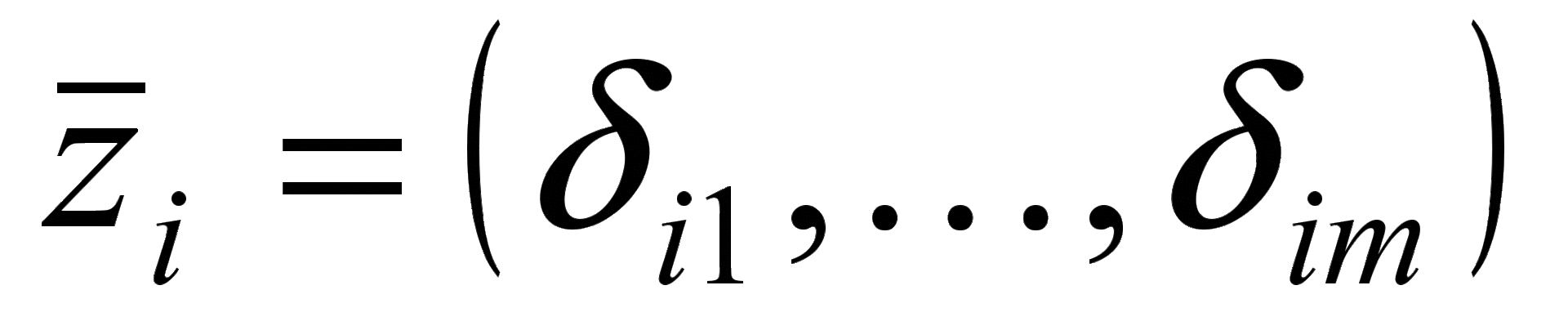 ,
,
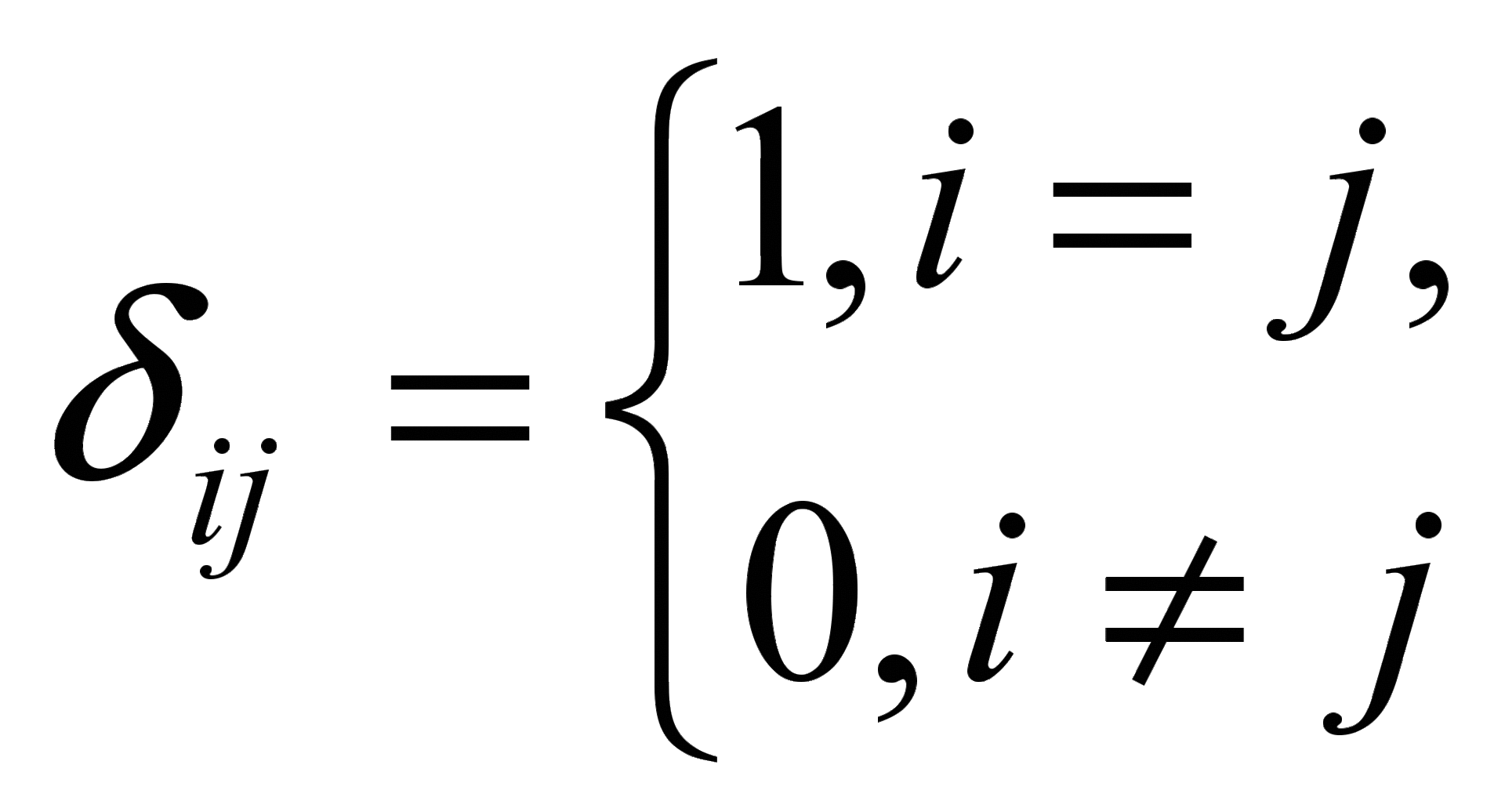 - Kronecker symbol,
- Kronecker symbol,
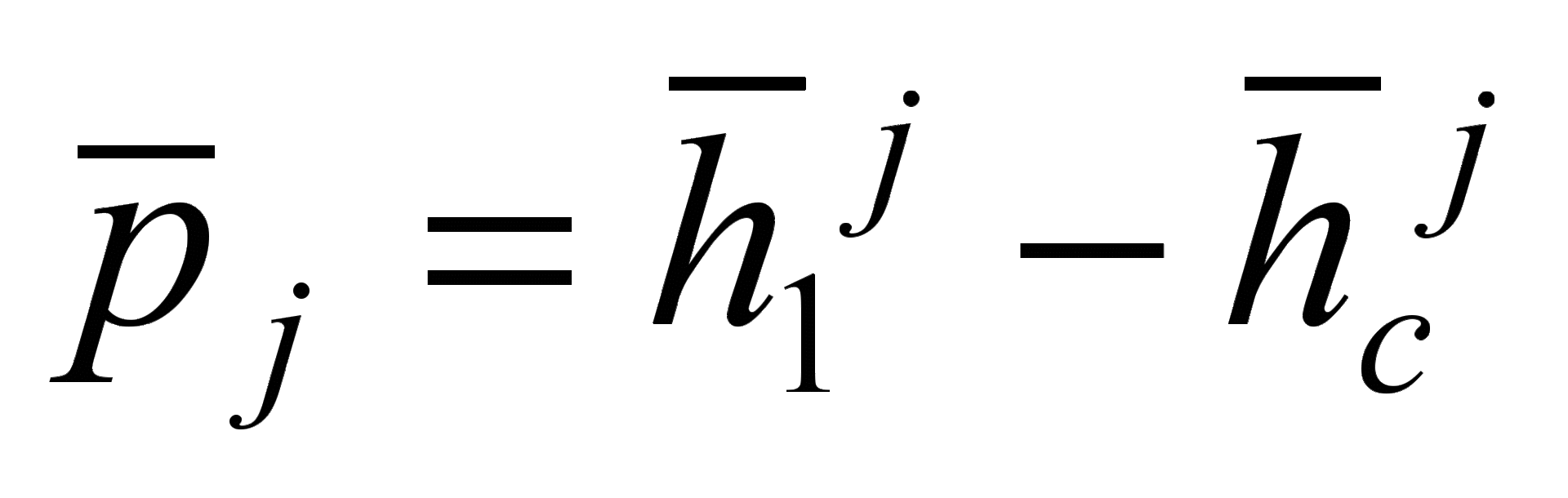 - vector of the direction of the j -th factor axis.
- vector of the direction of the j -th factor axis.
Correlations between the original variables can be defined as the scalar product of the normalized latter with zero mean and unit variance:

n is the dimension of the original variable space.
The correlation coefficients between the original variables determine the correlation matrix, which is similar to the mutual distance matrix of the multidimensional scaling method. Since the closest objects in the factor space correspond to large values of the correlation coefficients, the elements of the matrix of mutual distances d ij are obtained from the corresponding elements of the correlation matrix r ij by the formula:
 .
.
Using the Verlet method, the factor structure will be reconstructed within the framework of the dimension g of the factor space.
Elements of the factor structure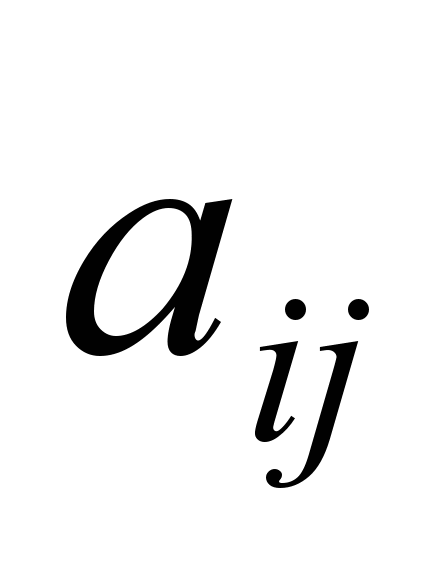 can be defined as the correlation coefficient between the j -th factor axis and the i -th variable:
can be defined as the correlation coefficient between the j -th factor axis and the i -th variable:
 ,
,
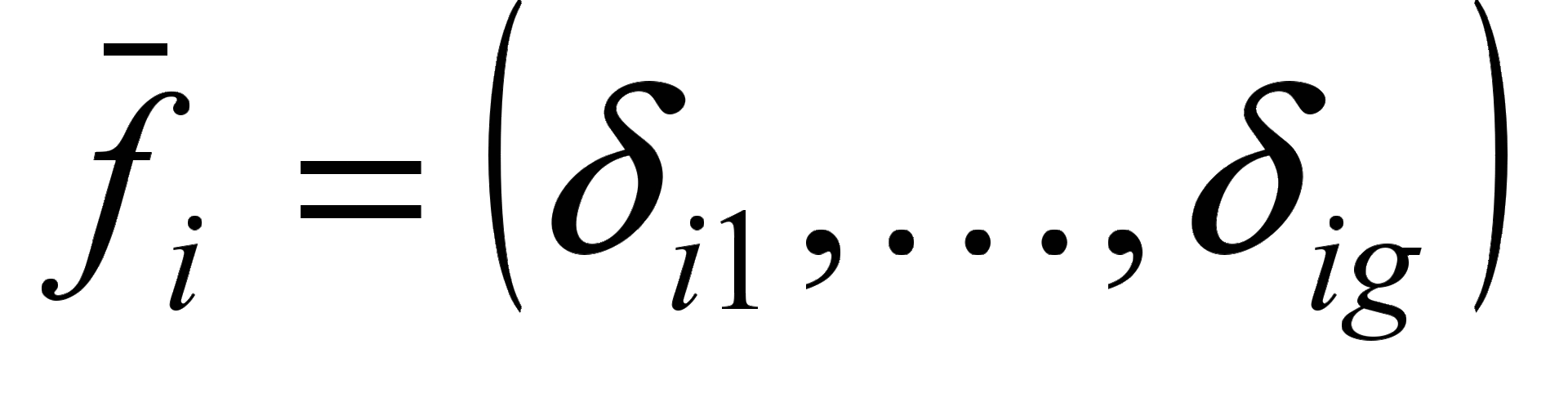 ,
,
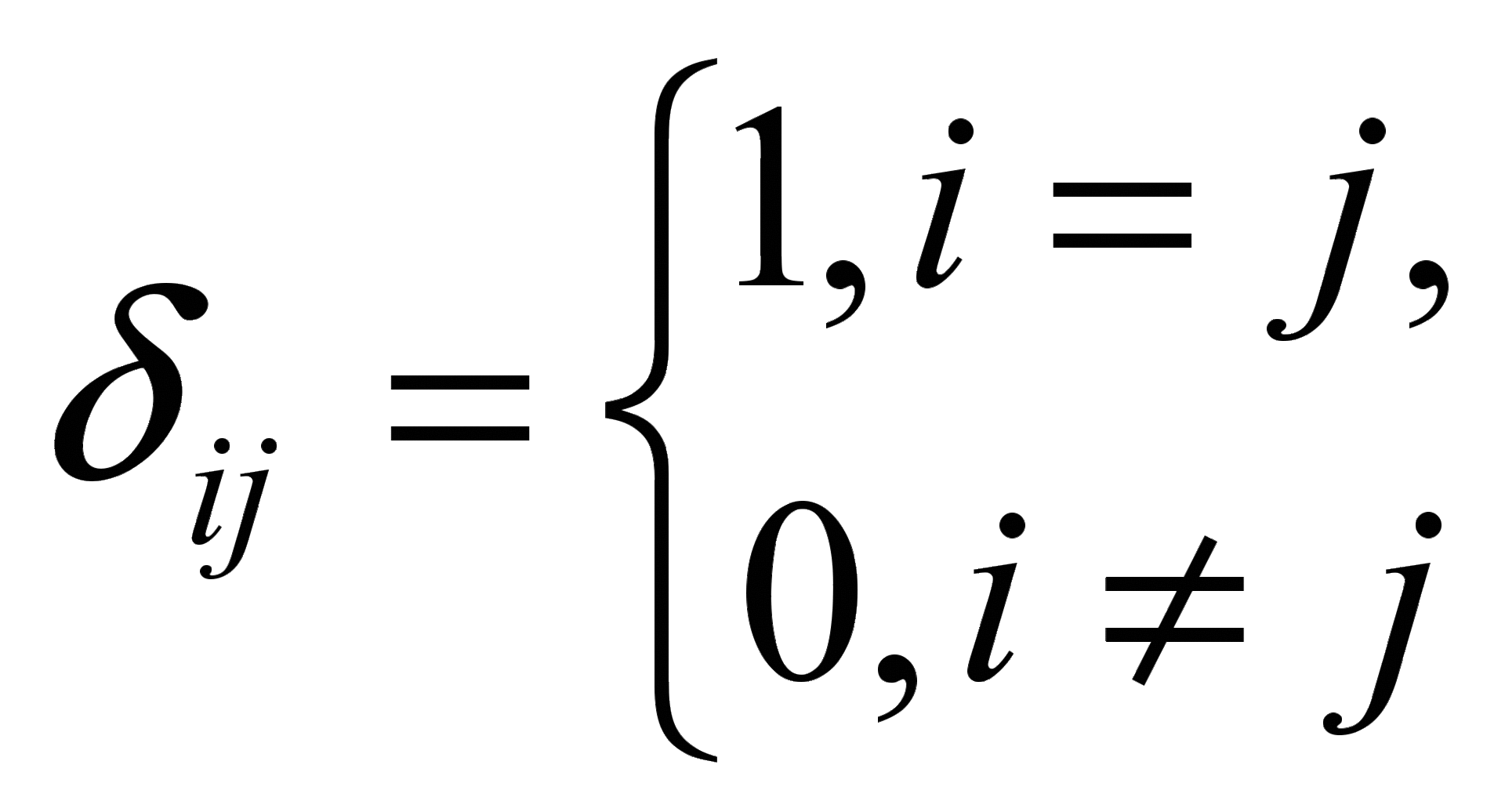 - Kronecker symbol,
- Kronecker symbol,
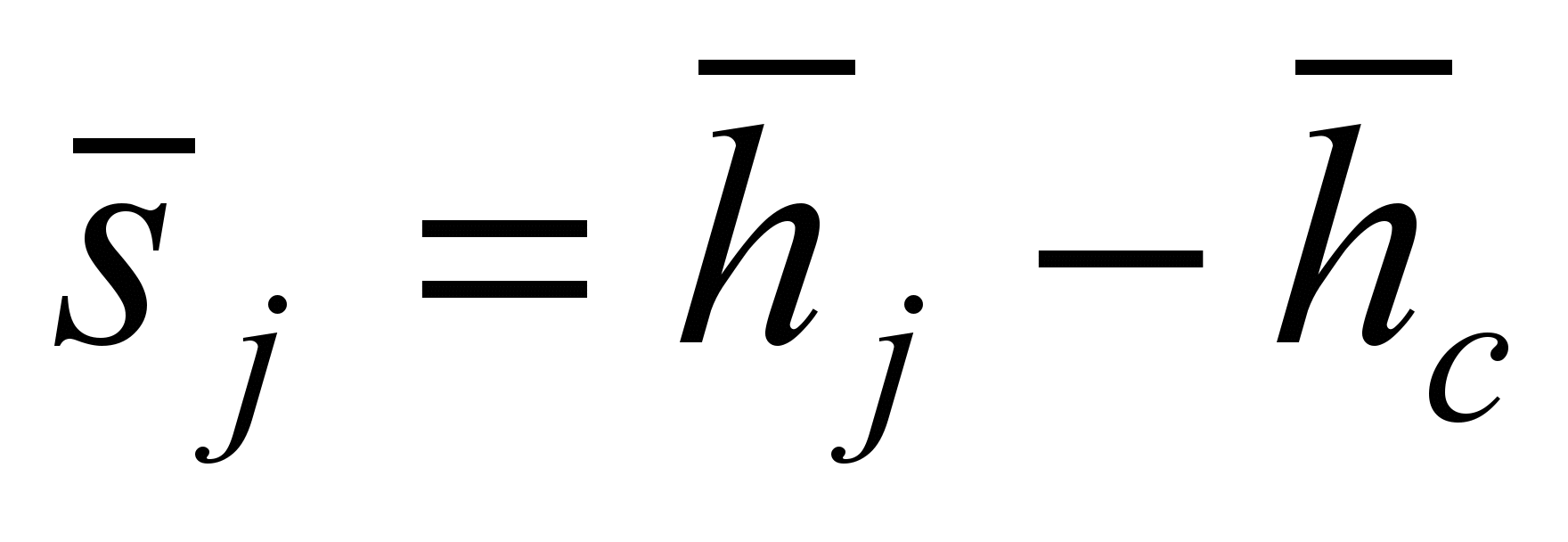 - the direction vector of the j -th variable in the factor space.
- the direction vector of the j -th variable in the factor space.
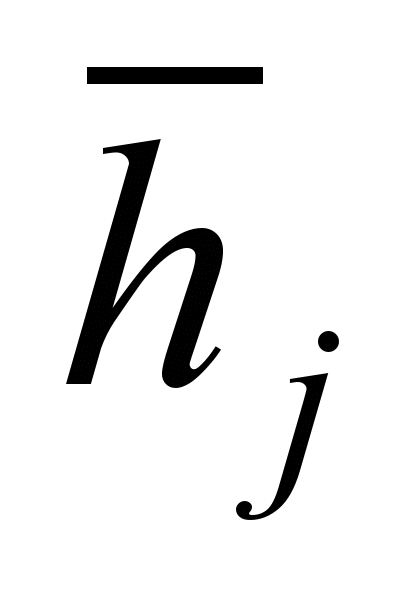 - j- th variable in the factor space.
- j- th variable in the factor space.
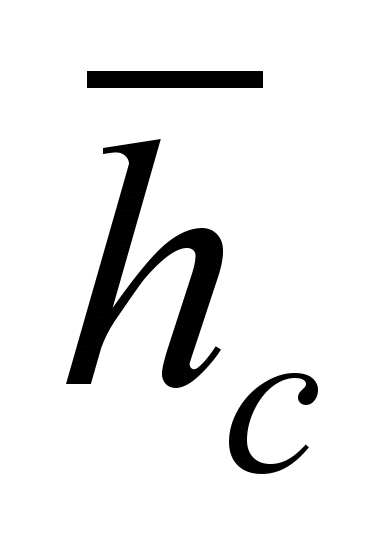 - the center of mass of the factor structure of variables in the factor space.
- the center of mass of the factor structure of variables in the factor space.
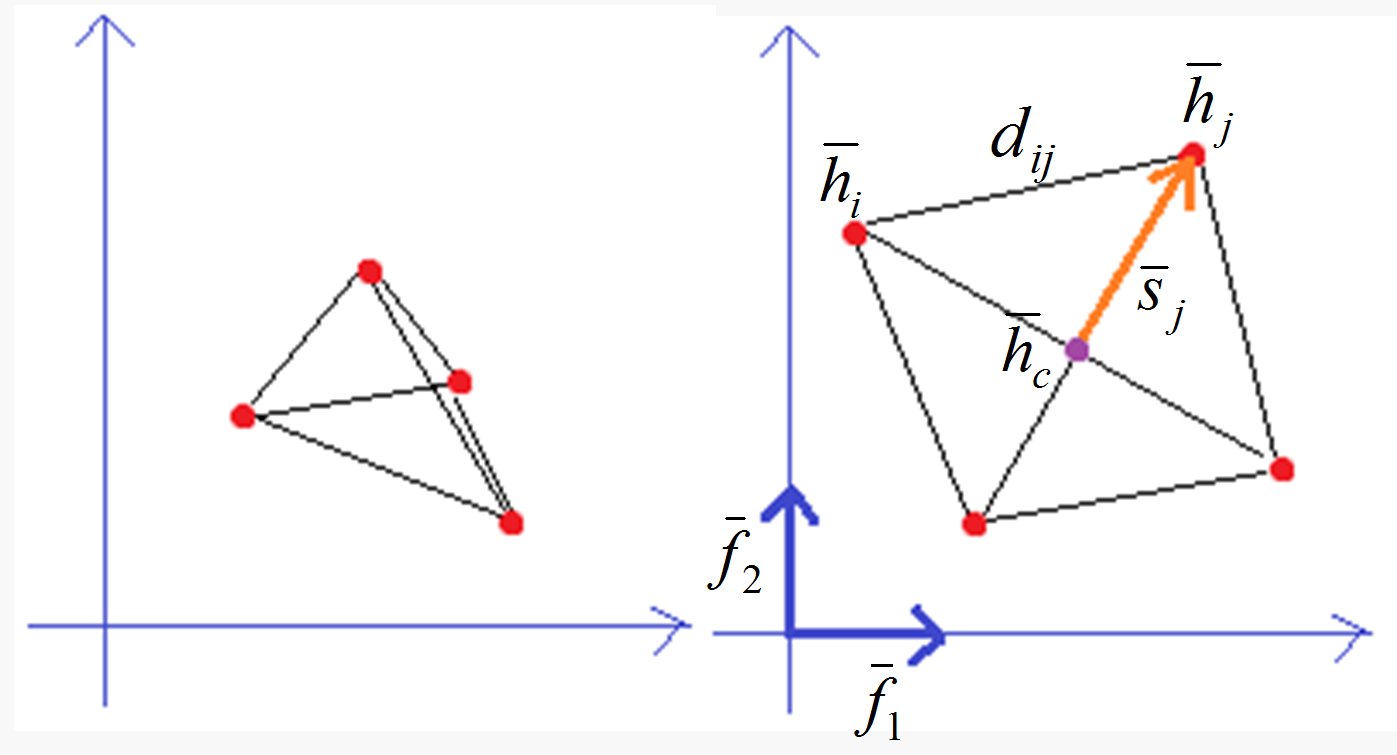
Fig. 4. Elastic multidimensional scaling structure
The Verle method was implemented programmatically using the Verlet.js open-source JavaScript library, which was enhanced for the multidimensional case. The Web application of factor analysis based on the method of calculating the elastic factor structure and multidimensional scaling based on the Verlet method is available at http://svlaboratory.org/application/pca and http://svlaboratory.org/application/mcal after registering a new user. The application allows you to visualize the process of convergence of the Verlet method in a given coordinate plane (Fig. 5).
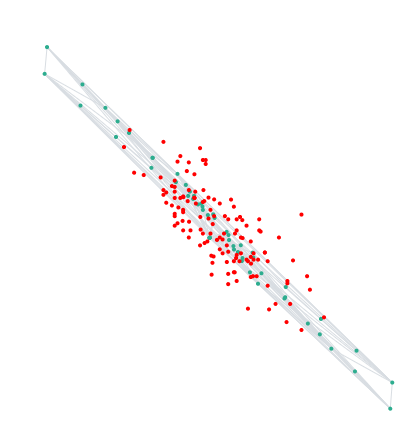

Fig. 5. Visualization of the Verlet method in a web application
The initial parameters were taken 15 biophysical indicators for 131 persons with hypertension at the initial stage:
1) weight
2) body mass index (BMI),
3) respiratory rate (RR),
4) segmented neutrophils (C),
5) lymphocytes (L),
6) end-systolic size of the left ventricle (DAC),
7) end-systolic volume of the left ventricle (CSR),
8) end-diastolic size of the left ventricle (CVD),
9) end-diastolic volume of the left ventricle (CDW),
10) stroke volume (PP),
11) cardiac output (MOS),
12) total peripheral vascular resistance (OPS),
13) the index of Hildebrandt (EM)
14) left ventricular ejection fraction (EF),
15) fraction of shortening of the left ventricle (FU).
The resulting factor structures for these hypertension are presented in Table 1, 2, 3.
Table 1. Initial factor solution (Verlet method of elastic factor structure)
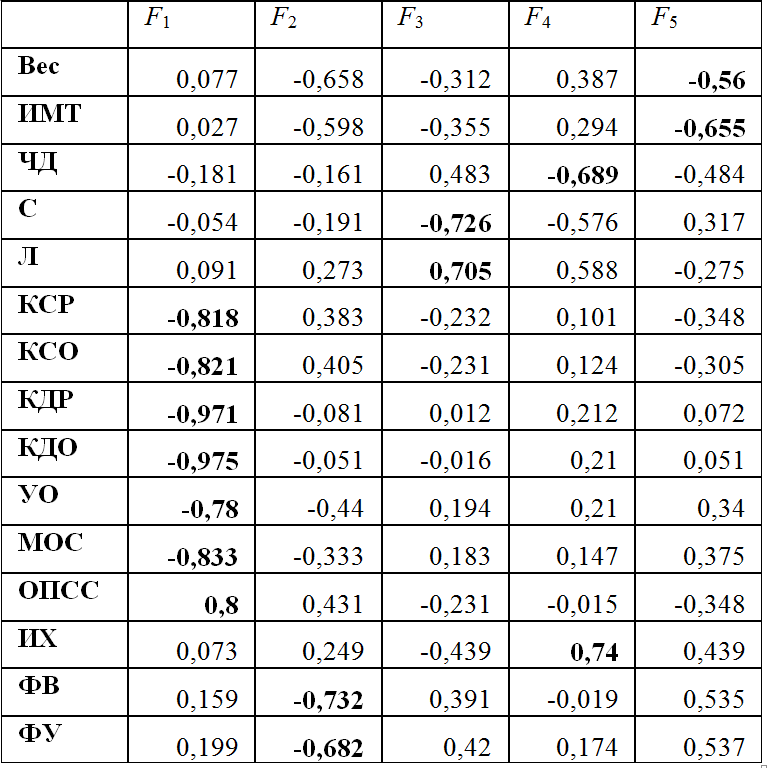
Table 2. The original factor solution (Verlet method of multidimensional scaling)
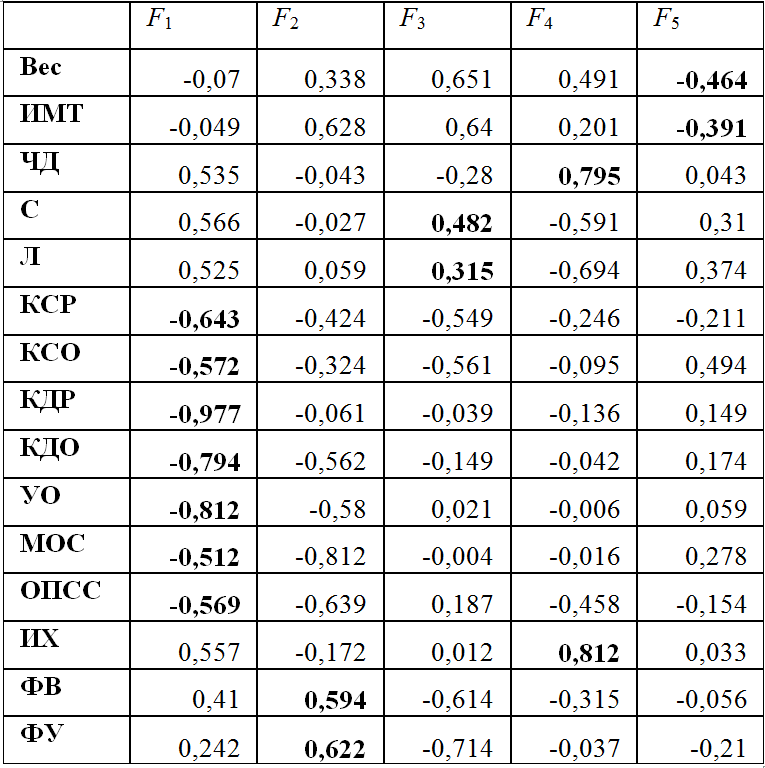
Table 3. Initial factor solution (eigenvector method)

Factor solutions after factor rotation according to the criterion of interpretability proposed in [1] are presented in Table 4, 5, 6. These factor structures are confirmed by previous works [2, 3].
Table 4. Factor structure by the criterion of interpretability (Verlet method of elastic factor structure)

Table 5. Factor structure by the criterion of interpretability (Verlet method of multidimensional scaling)

Table 6. Factor structure by the interpretability criterion (eigenvector method)
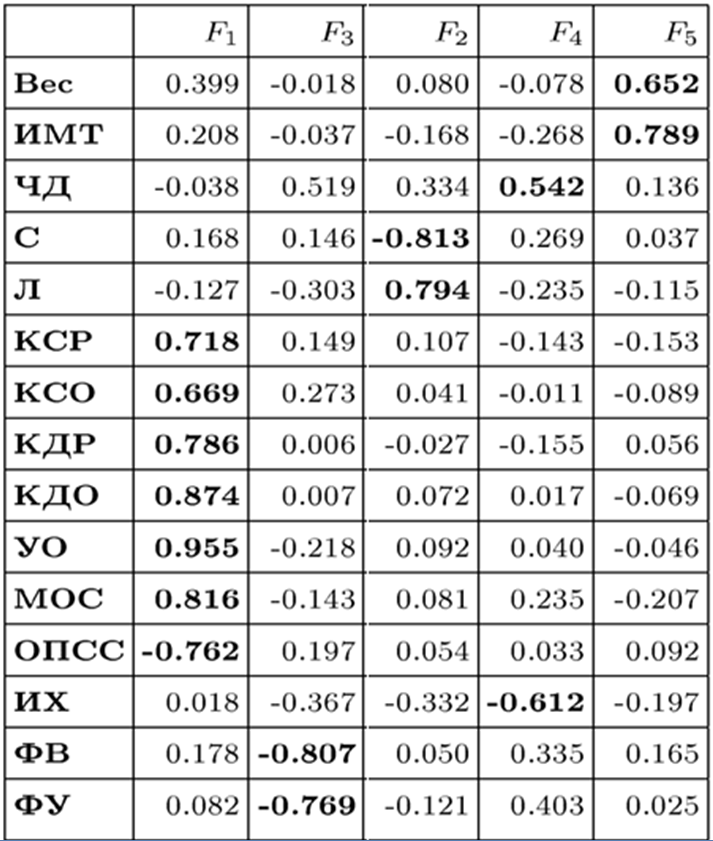
As an elastic structure, a multidimensional factor structure was used, containing factor axes and connections between different points of the factor axes. To approximate a set of points by an elastic structure, we used the Verlet method and the physical interpretation of data points in a multidimensional space as centers of attraction. The method of multidimensional scaling based on the Verlet method, applied to the correlation matrix, is an alternative method of factorization. An arbitrary structure can be used as a multidimensional elastic structure, thus the proposed approximation method based on the Verlet method has a generalized character.
Factor structures based on the Verlet method were obtained for 15 biophysical indicators of the initial stage of arterial hypertension. The obtained factor structures correlate well with the classical eigenvector method, and are also confirmed by the results of earlier works.
Elastic structure is the most common type of structure for approximating data. This is a set of knots and elastic connections between them. As such connections there may be a spring connection between a pair of points with an equilibrium distance between points and ribs of three nodes with an equilibrium angle between the nodes. To approximate a set of points by an elastic structure, it is proposed to use the physical interpretation of data points as centers attracting nodes of an elastic structure. A special case of an elastic structure is the nonlinear principal components. This is a set of elastic chains with a common point of intersection. With a high stiffness of elastic bonds, the nonlinear principal components transform into the classical principal components of factor analysis. To calculate the motion of points of an elastic structure in the field of attraction and taking into account the connections between the nodes of the elastic structure, it is proposed to use the Verlet numerical integration method.
The multidimensional scaling allows, within the framework of the hypothesis of the dimension of the target space, to arrange objects according to their mutual distances so that the reconstructed distances between the objects approach the empirical ones. Based on the Verlet method, it is proposed to carry out multidimensional scaling, thus the mutual distances between points will be taken into account with the greatest accuracy. The correlation matrix will act as a matrix of mutual distances. With the help of multidimensional scaling, the factorization of the correlation matrix will be implemented, thereby the factor structure of the data in the factor space will be restored. To obtain an interpretable solution, it is proposed to use separate methods of factor rotation applied to the recovered factor structure.
1. Verlet Method
The Verlet algorithm is used to calculate the following position of the point on the current and past:
')
 ,
,m is the dimension of space
 - the influence vector of the k- th center of attraction represented by the data point
- the influence vector of the k- th center of attraction represented by the data point Restrictions are imposed on the system of points: some of the points are connected by elastic rods of a given length.
The algorithm works as follows:
- 1. Calculate the new positions of points.
- 2. For each connection, the corresponding condition is satisfied.
- 3. Step 2 is repeated s times.
For example, s = 16.
The procedure for relaxation of communication is described by the following formulas:
If the link is represented by dots
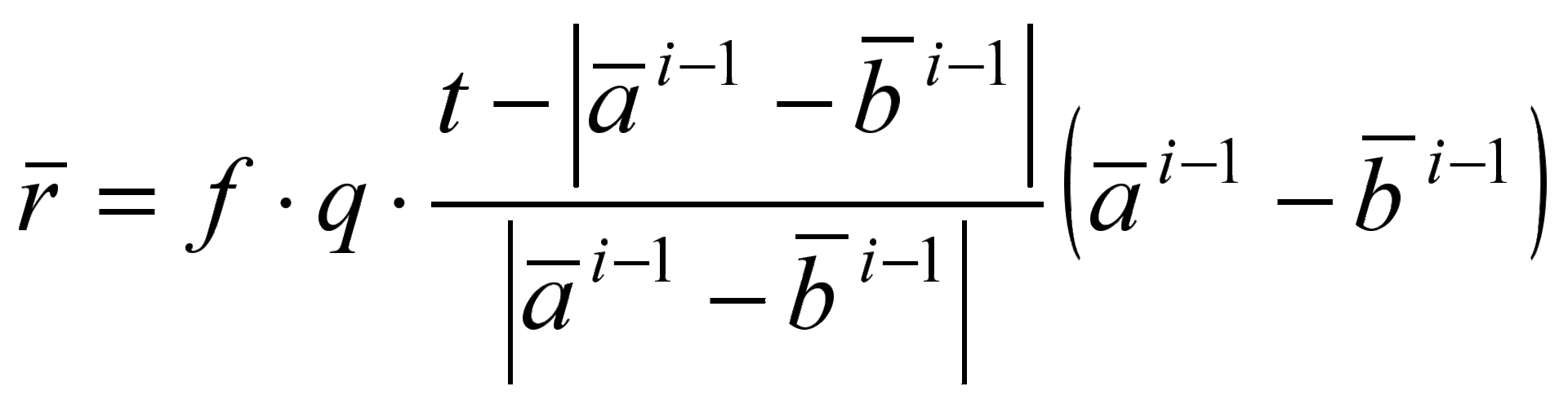 ,
, - coefficient depending on the number s of repetitions of step 2.
- coefficient depending on the number s of repetitions of step 2.
Fig. 1. Spring connection of a pair of points with an equilibrium distance
Triplets of knots can form stiffening ribs with an equilibrium angle. Such connections are proposed to be emulated by connections in the form of elastic rods between the extreme points. The equilibrium distance between the extreme points in this case is determined from the equality of the triangle. If the link is represented by dots

Fig. 2. Stiffener of three points with an equilibrium angle
2. Multidimensional scaling
Multidimensional scaling (MNSH) is a way of the most effective placement of objects, approximately keeping the distances observed between them. MNS places objects in a space of a given dimension and checks how accurately the resulting configuration maintains the distance between objects. MNSH uses the minimization algorithm for a certain function that evaluates the quality of the resulting display options.
The measure most commonly used to assess the quality of the fit model (mapping), measured by the degree of reproduction of the original matrix of similarities, is the so-called stress. The magnitude of the stress φ for the current configuration is defined as:
 .
.Here d ij are the reproduced distances in the space of a given dimension, and
δ ij is the initial distance.
m is the number of objects.
The function f (δ ij ) denotes a non-metric monotone transformation of the original data (distances). The MNSH does not reproduce the quantitative measures of the similarities of objects, but only their relative order. The smaller the stress value, the better the matrix of initial distances is consistent with the matrix of resulting distances.
3. Main components and factor model
The main component model is described by the following formulas:
m is the number of variables
g - the number of factors
4. Elastic factor structure
As a system of points for the Verlet method, the coordinate system represented by the axes can be used
w is the number of points forming the factor axis,
g is the number of factor axes.
For example, when

l is the distance between a pair of neighboring points forming the factor axis.
 - index of the center point of the factor axis.
- index of the center point of the factor axis.Pairs of points
Pairs of points
All pairs of points
Pairs of points


Fig. 3. Ways to set the factor structure for the Verlet method
Elements of the factor structure
 ,
,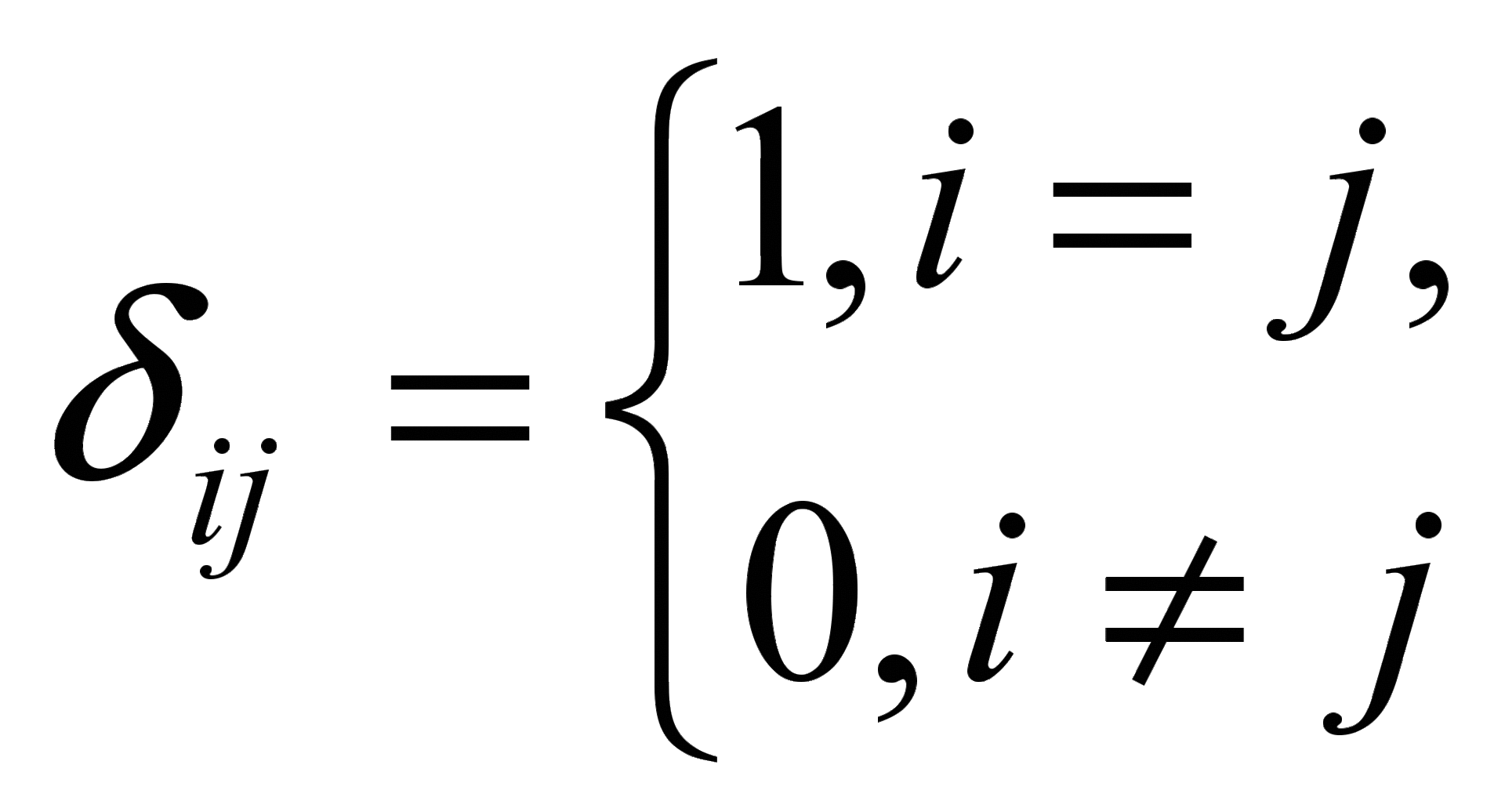 - Kronecker symbol,
- Kronecker symbol,5. Elastic Multidimensional Scaling Structure
Correlations between the original variables can be defined as the scalar product of the normalized latter with zero mean and unit variance:

n is the dimension of the original variable space.
The correlation coefficients between the original variables determine the correlation matrix, which is similar to the mutual distance matrix of the multidimensional scaling method. Since the closest objects in the factor space correspond to large values of the correlation coefficients, the elements of the matrix of mutual distances d ij are obtained from the corresponding elements of the correlation matrix r ij by the formula:
Using the Verlet method, the factor structure will be reconstructed within the framework of the dimension g of the factor space.
Elements of the factor structure
 ,
,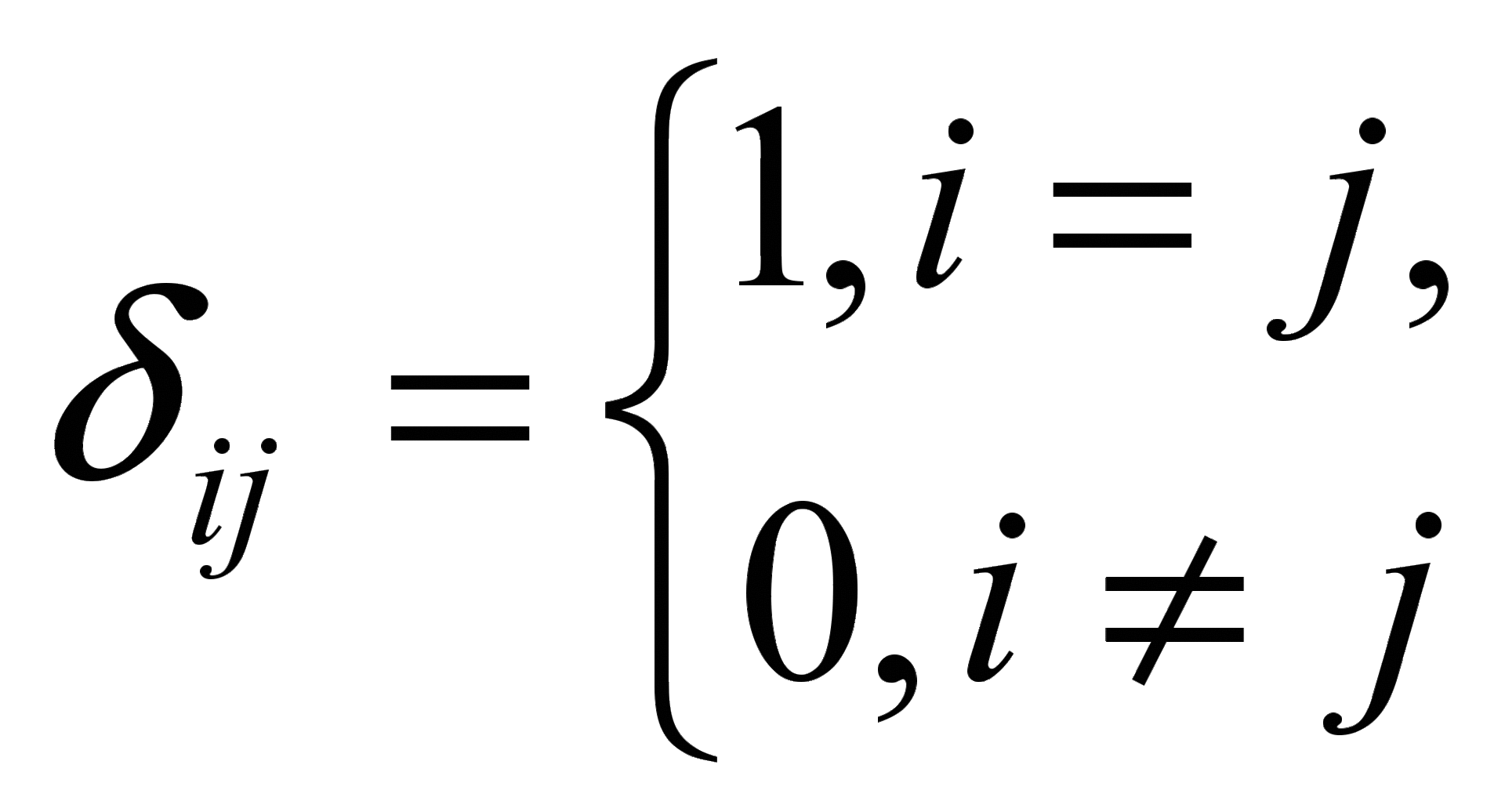 - Kronecker symbol,
- Kronecker symbol,
Fig. 4. Elastic multidimensional scaling structure
6. Software implementation
The Verle method was implemented programmatically using the Verlet.js open-source JavaScript library, which was enhanced for the multidimensional case. The Web application of factor analysis based on the method of calculating the elastic factor structure and multidimensional scaling based on the Verlet method is available at http://svlaboratory.org/application/pca and http://svlaboratory.org/application/mcal after registering a new user. The application allows you to visualize the process of convergence of the Verlet method in a given coordinate plane (Fig. 5).


Fig. 5. Visualization of the Verlet method in a web application
7. Numerical experiment
The initial parameters were taken 15 biophysical indicators for 131 persons with hypertension at the initial stage:
1) weight
2) body mass index (BMI),
3) respiratory rate (RR),
4) segmented neutrophils (C),
5) lymphocytes (L),
6) end-systolic size of the left ventricle (DAC),
7) end-systolic volume of the left ventricle (CSR),
8) end-diastolic size of the left ventricle (CVD),
9) end-diastolic volume of the left ventricle (CDW),
10) stroke volume (PP),
11) cardiac output (MOS),
12) total peripheral vascular resistance (OPS),
13) the index of Hildebrandt (EM)
14) left ventricular ejection fraction (EF),
15) fraction of shortening of the left ventricle (FU).
The resulting factor structures for these hypertension are presented in Table 1, 2, 3.
Table 1. Initial factor solution (Verlet method of elastic factor structure)

Table 2. The original factor solution (Verlet method of multidimensional scaling)

Table 3. Initial factor solution (eigenvector method)

Factor solutions after factor rotation according to the criterion of interpretability proposed in [1] are presented in Table 4, 5, 6. These factor structures are confirmed by previous works [2, 3].
Table 4. Factor structure by the criterion of interpretability (Verlet method of elastic factor structure)

Table 5. Factor structure by the criterion of interpretability (Verlet method of multidimensional scaling)

Table 6. Factor structure by the interpretability criterion (eigenvector method)

Conclusion
As an elastic structure, a multidimensional factor structure was used, containing factor axes and connections between different points of the factor axes. To approximate a set of points by an elastic structure, we used the Verlet method and the physical interpretation of data points in a multidimensional space as centers of attraction. The method of multidimensional scaling based on the Verlet method, applied to the correlation matrix, is an alternative method of factorization. An arbitrary structure can be used as a multidimensional elastic structure, thus the proposed approximation method based on the Verlet method has a generalized character.
Factor structures based on the Verlet method were obtained for 15 biophysical indicators of the initial stage of arterial hypertension. The obtained factor structures correlate well with the classical eigenvector method, and are also confirmed by the results of earlier works.
References
- 1. Chovin V. ., Goltyapin V. V. Methods of rotation of factor structures // Mathematical structures and modeling - 2015. № 2 (34). Pp. 75-84.
- 2. Goltyapin V.V., Shoovin V.A. Oblique factorial model of first stage arterial hypertension. // Bulletin of Omsk University. 2010. No. 4. c. 120-128.
- 3. Chovin V.A. Confirmatory factor model of arterial hypertension. // Computer research and modeling. 2012. V. 4. No. 4. c. 885-894.
Source: https://habr.com/ru/post/304270/
All Articles