How the principal component method (PCA) works with a simple example

In this article I would like to talk about exactly how the principal component component analysis (PCA) works from the point of view of the intuition behind its mathematical apparatus. As simple as possible, but in detail.

Mathematics is generally very beautiful and elegant science, but sometimes its beauty is hidden behind a bunch of layers of abstraction. It is best to show this beauty with simple examples, which, so to speak, can be twisted, played and felt, because in the end everything turns out to be much easier than it seems at first glance - the most important thing is to understand and imagine.

In data analysis, as in any other analysis, it is sometimes superfluous to create a simplified model that most accurately describes the real state of affairs. It often happens that the signs are quite dependent on each other and their simultaneous presence is redundant.
')
For example, our fuel consumption is measured in liters per 100 km, and in the United States in miles per gallon. At first glance, the values ​​are different, but in fact they are strictly dependent on each other. In a mile of 1600m, and in a gallon of 3.8l. One sign strictly depends on another, knowing one, we know and another.

But more often it happens that the signs depend on each other not so strictly and (importantly!) Not so clearly. Engine size as a whole has a positive effect on acceleration to 100 km / h, but this is not always the case. And it may also turn out that, taking into account factors that are not visible at first glance (such as improving fuel quality, using lighter materials and other modern advances), the year of the car is not much, but it also affects its acceleration.

Knowing the dependencies and their strength, we can express several signs through one, merge, so to speak, and work with a simpler model. Of course, most likely, it will not be possible to avoid information loss, but the PCA method will help us to minimize it.

To put it more strictly, this method approximates an n-dimensional cloud of observations to an ellipsoid (also n-dimensional), the semi-axes of which will be the future main components. And when projected on such axes (reduction of dimension), the greatest amount of information is saved.

Step 1. Data preparation

Here, for the sake of simplicity, I will not take real learning datasets for dozens of signs and hundreds of observations, but I will make my own, as simple as possible toy example. 2 signs and 10 observations will be quite enough to describe what, and most importantly - why, occurs in the depths of the algorithm.

Generate a sample:

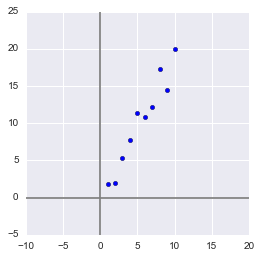
x = np.arange(1,11) y = 2 * x + np.random.randn(10)*2 X = np.vstack((x,y)) print X OUT: [[ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. ] [ 2.73446908 4.35122722 7.21132988 11.24872601 9.58103444 12.09865079 13.78706794 13.85301221 15.29003911 18.0998018 ]] 

In this sample, we have two signs that strongly correlate with each other. Using the PCA algorithm, we can easily find the sign-combination and, at the price of a piece of information, express both of these signs with one new one. So, let's understand!

First, some statistics. Recall that moments are used to describe a random variable. We need - mat. waiting and dispersion. You could say mate. Expectation is the “center of gravity” of a magnitude, and dispersion is its “size”. Roughly speaking, mat. the expectation specifies the position of the random variable, and the variance determines its size (more precisely, the spread).

The projection onto the vector itself does not affect the mean values, since to minimize information loss, our vector must pass through the center of our sample. Therefore, there is nothing terrible if we center our sample - we linearly shift it so that the average values ​​of the signs are equal to 0. This will greatly simplify our further calculations (although it is worth noting that you can do without centering).
The operator inverse to the shift will be equal to the vector of initial averages - it will be needed to restore the sample to its original dimension.

 Xcentered = (X[0] - x.mean(), X[1] - y.mean()) m = (x.mean(), y.mean()) print Xcentered print "Mean vector: ", m OUT: (array([-4.5, -3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5]), array([-8.44644233, -8.32845585, -4.93314426, -2.56723136, 1.01013247, 0.58413394, 1.86599939, 7.00558491, 4.21440647, 9.59501658])) Mean vector: (5.5, 10.314393916) 

Dispersion strongly depends on the orders of the values ​​of the random variable, i.e. sensitive to scaling. Therefore, if the units of measurement of signs vary greatly in their orders, it is highly recommended to standardize them. In our case, the values ​​do not vary much in order, so for the sake of simplicity, we will not perform this operation.

Step 2. Covariance matrix

In the case of a multidimensional random variable (random vector), the position of the center will still be mat. expectations of its projections on the axis. But to describe its shape, its axial dispersions are no longer enough. Look at these graphs, all three random variables have the same expectation and variance, and their projections on the axes as a whole will be the same!



To describe the shape of a random vector, a covariance matrix is ​​needed.

This is a matrix for which (i, j) -element is a correlation of signs (X _i , X _j ). Recall the covariance formula:



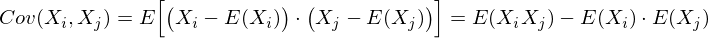
In our case, it is simplified, since E (X _i ) = E (X _j ) = 0:



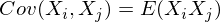
Note that when X _i = X _j :



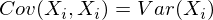
and this is true for any random variables.

Thus, in our matrix there will be dispersion of signs along the diagonal (since i = j), and in the other cells - covariances of the corresponding pairs of features. And due to the symmetry of the covariance, the matrix will also be symmetric.

Note: The covariance matrix is ​​a generalization of variance in the case of multidimensional random variables - it also describes the shape (variation) of a random variable, as does the variance.

Indeed, the dispersion of a one-dimensional random variable is a 1x1 covariance matrix, in which its single term is given by the formula Cov (X, X) = Var (X).

So, let's form a covariance matrix Σ for our sample. To do this, we calculate the variances of X _i and X _j , as well as their covariance. You can use the above formula, but since we are armed with Python, it's a sin not to use the numpy.cov (X) function. It takes as input a list of all attributes of a random variable and returns its covariance matrix and where X is an n-dimensional random vector (n is the number of rows). The function is excellent for calculating the unbiased dispersion, for the covariance of two quantities, and for compiling the covariance matrix.
(Let me remind you that in Python, the matrix is ​​represented by a column array of row arrays.)

 covmat = np.cov(Xcentered) print covmat, "\n" print "Variance of X: ", np.cov(Xcentered)[0,0] print "Variance of Y: ", np.cov(Xcentered)[1,1] print "Covariance X and Y: ", np.cov(Xcentered)[0,1] OUT: [[ 9.16666667 17.93002811] [ 17.93002811 37.26438587]] Variance of X: 9.16666666667 Variance of Y: 37.2643858743 Covariance X and Y: 17.9300281124 

Step 3. Eigenvectors and values ​​(ij pairs)

OK, we got a matrix that describes the shape of our random variable, from which we can get its dimensions in x and y (that is, X ₁ and X ₂ ), as well as an approximate shape on the plane. Now we need to find such a vector (in our case only one), at which the size (variance) of the projection of our sample on it would be maximized.

Note: The generalization of variance to higher dimensions is the covariance matrix, and these two concepts are equivalent. When projected onto a vector, the variance of the projection is maximized, and when projected onto spaces of higher orders, all its covariance matrix is ​​projected.

So, take the unit vector onto which we will project our random vector X. Then the projection onto it will be equal to v ^T X. The dispersion of the projection onto the vector will be equal to Var (v ^T X), respectively. In general, in vector form (for centered quantities), the variance is expressed as:



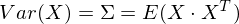
Accordingly, the projection variance:



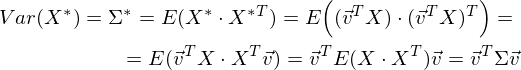
It is easy to see that the variance is maximized at the maximum value of v ^T Σv. Here Rayleigh's attitude will help us. Without going too deep into mathematics, I’ll just say that the Rayleigh relationship has a special case for covariance matrices:


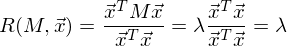
and


The latter formula should be familiar with the topic of the decomposition of the matrix into eigenvectors and values. x is an eigenvector, and λ is an eigenvalue. The number of eigenvectors and values ​​is equal to the size of the matrix (and the values ​​can be repeated).

By the way, in English, eigenvalues ​​and vectors are called eigenvalues and eigenvectors, respectively.
It seems to me that this sounds much more beautiful (and briefly) than our terms.

Thus, the direction of the maximum dispersion of the projection always coincides with the Igenvector, which has a maximum eigenvalue equal to the magnitude of this dispersion .

And this is also true for projections onto a larger number of dimensions — the variance (covariance matrix) of the projection onto the m-dimensional space will be maximum in the direction of the m highgenvectors with maximal eigenvalues.

The dimension of our sample is two and the number of aigenvectors for it, respectively, is 2. Find them.

The numpy library implements the numpy.linalg.eig (X) function, where X is a square matrix. It returns 2 arrays - an array of origin values ​​and an array of source vectors (column vectors). And the vectors are normalized - their length is 1. Just what we need. These 2 vectors define a new basis for the sample, such that its axes coincide with the semi-axes of the approximating ellipse of our sample.


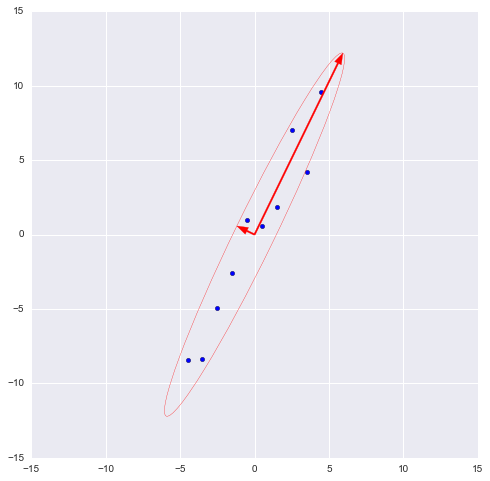
On this graph, we approximated our sample with an ellipse with radii of 2 sigma (i.e., it should contain 95% of all observations - which, in principle, we are seeing here). I have inverted a larger vector (the function eig (X) sent it in the opposite direction) - the direction, not the orientation of the vector, is important for us.

Step 4. Reduction dimension (projection)

The largest vector has a direction similar to the regression line and, having projected our sample onto it, we lose information comparable to the sum of the residual regression members (only the distance is now Euclidean, not the delta in Y). In our case, the relationship between the signs is very strong, so that the loss of information will be minimal. The “price” of the projection — dispersion along the smaller igengenctor — as seen from the previous graph, is very small.

Note: the diagonal elements of the covariance matrix show the variances according to the initial basis, and its eigenvalues ​​- according to the new (according to the main components).

It is often required to estimate the amount of information lost (and stored). It is most convenient to present in percentage. We take the variances along each axis and divide by the total sum of the variances along the axes (that is, the sum of all the eigenvalues ​​of the covariance matrix).
Thus, our larger vector describes 45.994 / 46.431 * 100% = 99.06%, and the smaller one, respectively, approximately 0.94%. Rejecting a smaller vector and projecting the data to a larger one, we lose less than 1% of the information! Excellent result!

Note: In practice, in most cases, if the total loss of information is no more than 10-20%, then you can safely reduce the dimension.

To carry out the projection, as mentioned earlier in step 3, it is necessary to carry out the operation v ^T X (the vector must be of length 1). Or, if we have not one vector, but a hyperplane, then instead of vector v ^T we take the matrix of basis vectors V ^T. The resulting vector (or matrix) will be an array of projections of our observations.

 _, vecs = np.linalg.eig(covmat) v = -vecs[:,1]) Xnew = dot(v,Xcentered) print Xnew OUT: [ -9.56404107 -9.02021624 -5.52974822 -2.96481262 0.68933859 0.74406645 2.33433492 7.39307974 5.3212742 10.59672425] 

dot (X, Y) - term by product (as we multiply vectors and matrices in Python)

It is easy to see that the values ​​of the projections correspond to the picture in the previous graph.

Step 5. Data Recovery

It is convenient to work with projection, build hypotheses on its basis and develop models. But not always obtained the main components will have a clear, understandable to a stranger, meaning. Sometimes it is useful to decode, for example, the detected outliers, in order to see what they are observing.

It is very simple. We have all the necessary information, namely, the coordinates of the basis vectors in the original basis (the vectors on which we have projected) and the vector of means (to cancel the alignment). Take, for example, the largest value: 10.596 ... and decode it. To do this, multiply it on the right by the transposed vector and add the vector of averages, or in general, for the entire sample: X ^T v ^T + m

 n = 9 #    Xrestored = dot(Xnew[n],v) + m print 'Restored: ', Xrestored print 'Original: ', X[:,n] OUT: Restored: [ 10.13864361 19.84190935] Original: [ 10. 19.9094105] 

The difference is small, but it is. After all, lost information is not restored. However, if simplicity is more important than accuracy, the reconstructed value perfectly approximates the original one.

Instead of a conclusion - check the algorithm

So, we have disassembled the algorithm, showed how it works on a toy example, now it remains only to compare it with the PCA implemented in sklearn - because we will use it.

 from sklearn.decomposition import PCA pca = PCA(n_components = 1) XPCAreduced = pca.fit_transform(transpose(X)) 

The n_components parameter indicates the number of dimensions for which the projection will be made, that is, up to how many dimensions we want to reduce our data. In other words, these are n iigenvectors with the largest eigenvalues. Check the result of reducing the dimension:

 print 'Our reduced X: \n', Xnew print 'Sklearn reduced X: \n', XPCAreduced OUT: Our reduced X: [ -9.56404106 -9.02021625 -5.52974822 -2.96481262 0.68933859 0.74406645 2.33433492 7.39307974 5.3212742 10.59672425] Sklearn reduced X: [[ -9.56404106] [ -9.02021625] [ -5.52974822] [ -2.96481262] [ 0.68933859] [ 0.74406645] [ 2.33433492] [ 7.39307974] [ 5.3212742 ] [ 10.59672425]] 

We returned the result as a matrix of column vector observations (this is a more canonical form from the point of view of linear algebra), while PCA returns a vertical array to sklearn.

In principle, this is not critical, it is simply worth noting that in linear algebra, matrix canonically be written through column vectors, and in data analysis (and other DB-related areas) observations (transactions, records) are usually written in rows.

We also check other model parameters — the function has a number of attributes that allow access to intermediate variables:

- Medium vector: mean_
- Projection vector (matrix): components_
- Dispersion of the axes of the projection (selective): explained_variance_
- Information share (share of total variance): explained_variance_ratio_

Note: explained_variance_ shows the sample variance, while the cov () function for building the covariance matrix calculates unbiased variances!

Let's compare our values ​​with the values ​​of the library function.

 print 'Mean vector: ', pca.mean_, m print 'Projection: ', pca.components_, v print 'Explained variance ratio: ', pca.explained_variance_ratio_, l[1]/sum(l) OUT: Mean vector: [ 5.5 10.31439392] (5.5, 10.314393916) Projection: [[ 0.43774316 0.89910006]] (0.43774316434772387, 0.89910006232167594) Explained variance: [ 41.39455058] 45.9939450918 Explained variance ratio: [ 0.99058588] 0.990585881238 

The only difference is in the variances, but as already mentioned, we used the cov () function, which uses unbiased variance, whereas the explained_variance_ attribute returns selective. They differ only in the fact that the first divides by (n-1) to get a mathematical expectation, and the second divides by n. It is easy to verify that 45.99 ∙ (10 - 1) / 10 = 41.39.

All other values ​​are the same, which means that our algorithms are equivalent. And finally, I note that the attributes of the library algorithm have less accuracy, since it is probably optimized for speed, or just rounds the values ​​for convenience (or I have some glitches).

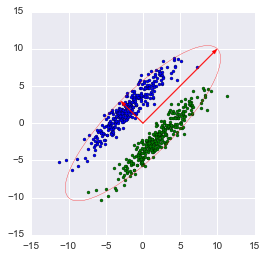
Note: the library method automatically projects on the axes that maximize dispersion. It is not always rational. For example, in this figure, an inaccurate reduction in dimensionality will lead to the fact that the classification will become impossible. However, the projection onto a smaller vector will successfully reduce the dimension and preserve the classifier.

So, we reviewed the principles of the PCA algorithm and its implementation in sklearn. I hope this article was clear enough for those who are just starting to become familiar with data analysis, and also at least a little informative for those who know this algorithm well. An intuitive presentation is extremely useful for understanding how a method works, and understanding is very important for correct tuning of the selected model. Thanks for attention!

PS: Please do not scold the author for possible inaccuracies. The author himself is in the process of exploring the data analysis and wants to help the same as he is in the process of mastering this amazing field of knowledge! But constructive criticism and diverse experience are strongly encouraged!