Developing a script to compare people's tastes
Greetings,% username%. Today, we will develop a script for compiling a ranking of similarity of interests between people.
Interested? I ask under the cat
')
I would like to note that this method works effectively only for the greatest relationship between the number of characteristics of a set and the number of sets. Otherwise I recommend using this method.
So let's start from afar. Imagine two some data sets. We call them p and q . Let each of these sets characterize two numbers. Then we represent these sets as points in the space L with the dimension dimL = n, where n is the number of characteristics. In this case, 2
p (p1; p2) and q (q1; q2)
We define some metric d (p, q) = k, where k is a coefficient. the differences of the two sets. We define the metric as the Euclidean distance between these two points, that is, from the angeme course we know:
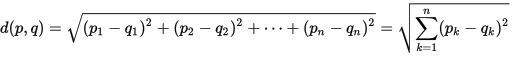
By our definition, it follows that the difference between two sets is the distance between the points with which we compare our sets. Then the difference between the two data sets is found by the Pythagorean theorem, oh how!
Then for two identical sets the distance will be zero.
Consider an example. Take two subjects, let's call them Vasya (B) and Kohl (K). Ask them questions:
1) - Rate on a 10-point scale how much you like peaches
2) - Rate on a 10-point scale how much do you like strawberries
Suppose that Vasya and Kolya answered the same way. Then, obviously, the distance between the points will be zero, that is, in these sets of their interests / tastes they are identical. Consider now the case of different answers.
B: on (1) gave 5, on (2) gave 8
K: on (3) gave 10, on (2) gave 0
Then we can imagine in a two-dimensional space points for Kolya and Vasya:
In (5; 8) and K (10; 0), the distance between them, as it is easy to calculate 9.4. This is the coefficient. the differences. But ... wait, how to interpret it?
Let's get a look. The minimum difference is zero with complete coincidence of the sets, this is understandable. But what about the maximum? Consider some delta neighborhood on our plane. since the maximum number of points is 10, then the delta will be equal to 10, that is, according to the Pythagorean theorem, sqrt (100 + 100) = 14.14 - this is the maximum difference at which data sets can be considered opposite. Thus, Kolya and Vasya in this case have more differences than similarities.
Applications can be found anywhere. Dating sites, freelance sites, job sites, etc. Creating questionnaires, you can create a certain map of interests and tastes by which you can find couples for relationships. Love, friendship, labor, any.
We implement the example of mapping the interests of people. And at once we will test, on the example of my friends.
We will use python, since this PL is most suitable for implementing such algorithms. First of all, due to the convenience of working with dictionaries (hashes / associative arrays), as well as thanks to the smart built-in module pickle, which will allow us to save dictionaries with questions and answers directly to disk and then use it. By tradition, all the code can be viewed at the end of the article.
To calculate the metric we will use the following code:
The function takes a tuple of two numbers that tell which data sets to analyze (data sets are stored in the dictionary of the dictionary, where the keys are the number of the set) that are in the Points dictionary.
The function returns the coefficient. the differences of the two sets.
In order to "map" the interests we need to analyze each set, not just two. For this there is a function:
The function generates a set relationship map and outputs to stdout.
Ohoho how it sounds. Now let's play. We make this list of questions:
And let us answer each user by creating a data set. At once I will tell, in the program the data set is numbered as they are loaded through pickle. Therefore, the output is, respectively, the numbers in the format (number - number = coefficient of difference).
For readability, I manually reprinted them in the last names, replacing them with random ones for the article (consent to sample data was not received from everyone).
Starting mapping we get the following:
How to interpret this? Let's see, we had 13 questions in total. The maximum number of points is 10
Then, by the Pythagorean theorem, we find the largest possible distance in the vicinity of a 13-dimensional space:
sqrt (100 * 13) = 36,056
Average value = maximum / 2 = 16.03
Thus, we see that basically we have more in common with friends (this is logical).
And only the rating of the difference between Azarova and Petrova shows that these two friends of mine (girlfriend) are the most different in their interests, since their coefficients are. equal to 17.66, which is more than the average.
Thus, this method can be used to rank users according to their interests on dating sites. We see that the more questions, the more accurate the comparison of personalities. By creating, for example, when registering a questionnaire of 100 questions and making a map for a small social network (as the amount of memory for this method grows linearly with the increase in users), we can recommend people to communicate / learn.
Interested? I ask under the cat
')
Instead of intro
I would like to note that this method works effectively only for the greatest relationship between the number of characteristics of a set and the number of sets. Otherwise I recommend using this method.
Theory
So let's start from afar. Imagine two some data sets. We call them p and q . Let each of these sets characterize two numbers. Then we represent these sets as points in the space L with the dimension dimL = n, where n is the number of characteristics. In this case, 2
p (p1; p2) and q (q1; q2)
We define some metric d (p, q) = k, where k is a coefficient. the differences of the two sets. We define the metric as the Euclidean distance between these two points, that is, from the angeme course we know:
By our definition, it follows that the difference between two sets is the distance between the points with which we compare our sets. Then the difference between the two data sets is found by the Pythagorean theorem, oh how!
Then for two identical sets the distance will be zero.
And what does it all mean?
Consider an example. Take two subjects, let's call them Vasya (B) and Kohl (K). Ask them questions:
1) - Rate on a 10-point scale how much you like peaches
2) - Rate on a 10-point scale how much do you like strawberries
Suppose that Vasya and Kolya answered the same way. Then, obviously, the distance between the points will be zero, that is, in these sets of their interests / tastes they are identical. Consider now the case of different answers.
B: on (1) gave 5, on (2) gave 8
K: on (3) gave 10, on (2) gave 0
Then we can imagine in a two-dimensional space points for Kolya and Vasya:
In (5; 8) and K (10; 0), the distance between them, as it is easy to calculate 9.4. This is the coefficient. the differences. But ... wait, how to interpret it?
Let's get a look. The minimum difference is zero with complete coincidence of the sets, this is understandable. But what about the maximum? Consider some delta neighborhood on our plane. since the maximum number of points is 10, then the delta will be equal to 10, that is, according to the Pythagorean theorem, sqrt (100 + 100) = 14.14 - this is the maximum difference at which data sets can be considered opposite. Thus, Kolya and Vasya in this case have more differences than similarities.
And why is this all?
Applications can be found anywhere. Dating sites, freelance sites, job sites, etc. Creating questionnaires, you can create a certain map of interests and tastes by which you can find couples for relationships. Love, friendship, labor, any.
We implement the example of mapping the interests of people. And at once we will test, on the example of my friends.
We will use python, since this PL is most suitable for implementing such algorithms. First of all, due to the convenience of working with dictionaries (hashes / associative arrays), as well as thanks to the smart built-in module pickle, which will allow us to save dictionaries with questions and answers directly to disk and then use it. By tradition, all the code can be viewed at the end of the article.
To calculate the metric we will use the following code:
Metric calculation
def calc(nPoint): result = 0.0 print("sqrt(", end="") for key in Dictionary: print("(", Points[nPoint[0]][key], " - ", Points[nPoint[1]][key], ")^2 + ", sep="", end="") result = result + math.pow((Points[nPoint[0]][key] - Points[nPoint[1]][key]),2) print(")") result = math.sqrt(result) return result The function takes a tuple of two numbers that tell which data sets to analyze (data sets are stored in the dictionary of the dictionary, where the keys are the number of the set) that are in the Points dictionary.
The function returns the coefficient. the differences of the two sets.
In order to "map" the interests we need to analyze each set, not just two. For this there is a function:
Generation coefficients for each set
def GenerateMap(): print("~~~~") for i in range(1, PSize): for j in range(i + 1, PSize + 1): print(i, " and ", j, " = ", calc( (i, j) ), sep="") The function generates a set relationship map and outputs to stdout.
Script testing in humans
Ohoho how it sounds. Now let's play. We make this list of questions:
A list of questions
1) ? (0- , 10- )
2) (0- , 10 )
3) ?(0- , 10- )
4) ?(0- , 10- )
5) ? (0- , 10 )
6) ? (0- , 10 )
7) ? (0- , 10 )
8) ? (0- , 10 )
9) ? (0, 10)
10) ? ( 0, 10)
11) (0, 10)
12) (0, 10)
13) (0, 10)
And let us answer each user by creating a data set. At once I will tell, in the program the data set is numbered as they are loaded through pickle. Therefore, the output is, respectively, the numbers in the format (number - number = coefficient of difference).
For readability, I manually reprinted them in the last names, replacing them with random ones for the article (consent to sample data was not received from everyone).
Starting mapping we get the following:
Exhaust
- = 11.83
- = 12.72
- = 12.92
- = 12.88
- = 16.49
- = 9.59
- = 8.77
- = 10
- = 14.28
- = 10.34
- = 13.85
- = 12.4
- = 12.68
- = 14.93
- = 17.66
How to interpret this? Let's see, we had 13 questions in total. The maximum number of points is 10
Then, by the Pythagorean theorem, we find the largest possible distance in the vicinity of a 13-dimensional space:
sqrt (100 * 13) = 36,056
Average value = maximum / 2 = 16.03
Thus, we see that basically we have more in common with friends (this is logical).
And only the rating of the difference between Azarova and Petrova shows that these two friends of mine (girlfriend) are the most different in their interests, since their coefficients are. equal to 17.66, which is more than the average.
Instead of conclusion
Thus, this method can be used to rank users according to their interests on dating sites. We see that the more questions, the more accurate the comparison of personalities. By creating, for example, when registering a questionnaire of 100 questions and making a map for a small social network (as the amount of memory for this method grows linearly with the increase in users), we can recommend people to communicate / learn.
Full code
#!/usr/bin/python import sys import pickle import math Dictionary = [] Points = {} PSize = 0 def DictGen(): print("~~~~") DictList = [] print("For exit enter a \"0\"") while True: s = str(input("> ")) if (s == "0"): break; else: DictList.append(s) print("Enter a name for new list of keys: ") fname = str(input("> ")) with open(fname, 'wb') as f: pickle.dump(DictList, f) print("Saved with name ", fname, sep = "") def DictLoad(): print("~~~~") fname = str(input("Enter a name of list to load\n> ")) with open(fname, 'rb') as f: Dictionary.clear() Dictionary.extend(pickle.load(f)) def NewPoint(): print("~~~~") if (not Dictionary): print("List of keys not loaded (command 2)") else: LocalPoint = {} for key in Dictionary: print(key, ": ", sep="", end="") mark = float(input()) LocalPoint[key] = mark print("Enter a name for new point: ") fname = str(input("> ")) with open(fname, 'wb') as f: pickle.dump(LocalPoint, f) print("New point saved with name ", fname, sep="") def LoadPoint(): print("~~~~") fname = str(input("Enter a name of point to load\n> ")) with open(fname, 'rb') as f: LocalPoint = pickle.load(f) Points[PSize] = LocalPoint def calc(nPoint): result = 0.0 print("sqrt(", end="") for key in Dictionary: print("(", Points[nPoint[0]][key], " - ", Points[nPoint[1]][key], ")^2 + ", sep="", end="") result = result + math.pow((Points[nPoint[0]][key] - Points[nPoint[1]][key]),2) print(")") result = math.sqrt(result) return result def GenerateMap(): print("~~~~") for i in range(1, PSize): for j in range(i + 1, PSize + 1): print(i, " and ", j, " = ", calc( (i, j) ), sep="") while True: print("0 - exit") print("1 - generate a list of keys") print("2 - load a map of marks") print("3 - add a new point in dimension") print("4 - load a new point in dimension") print("5 - calculate distance from two points of dimension") print("6 - print information") print("7 - create a map with distance for every point") i = int(input("#-> ")) if (i == 0): sys.exit() elif (i == 1): DictGen() elif (i == 2): DictLoad() elif (i == 3): NewPoint() elif (i == 4): PSize = PSize + 1 LoadPoint() elif (i == 5): print("Enter a two numbers of which points you want to calculate a distance") nPoint = tuple(int(x.strip()) for x in input().split(' ')) print("Difference: ", calc(nPoint), sep="") input() sys.exit() elif (i == 6): print("Dictionary", Dictionary, sep = ": ") print("Points: ", Points, sep = ": ") print("Total points: ", PSize, sep = "") elif (i == 7): GenerateMap() else: print("Unknown command") sys.exit() Source: https://habr.com/ru/post/304082/
All Articles