What is space time really?

Translation of Stephen Wolfram's post " What Is Spacetime, Really? ".
I express my deep gratitude to Kirill Guzenko KirillGuzenko for his help in translating and preparing the publication.

Note: This post by Stephen Wolfram is inextricably linked with the theory of cellular automata and other related concepts, as well as with his book A New Kind of Science , which contains a large number of references from this article. The post illustrates well the use of programming in the scientific field, in particular, Stephen shows (the code is given in the book) many examples of programming in the Wolfram Language in the fields of physics, mathematics, computability theory, discrete systems, etc.

---

Content

Simple theory of everything?
Universe data structure
Space as a graph
Maybe there is nothing but space
What is time?
Network formation
Conclusion STO
Conclusion of GR (General Relativity)
Particles, quantum mechanics, etc.
In search of the universe
Ok show me the universe
Do physics or not - that is the question
What is needed?
But has the time come?

---

One hundred years ago, Albert Einstein published the general theory of relativity - a brilliant, elegant theory that has survived a century and opened the only successful path to the description of space-time ( space-time continuum ).

There are many different points in theory that indicate that the general theory of relativity is not the last point in the history of spacetime. Indeed, let me like GTR as an abstract theory, but I came to the conclusion that it might have led us away from the path of understanding the true nature of space and time for a whole century.
')
I thought about the device of space and time for a little more than forty years. In the beginning, as a young theoretical physicist, I simply accepted the Einstein mathematical formulation of the problem of special and general relativity, and also did some work in quantum field theory, cosmology, and other fields, based on it.

But about 35 years ago, partly inspired by my experience in the technical fields, I began to explore in more detail the fundamental issues of theoretical science, from which I began my long way of going beyond the traditional mathematical equations and using calculations and programs instead of them as basic models in science. Soon after, I happened to find out that even very simple programs can exhibit very complex behavior, and then, years later, I discovered that systems of any kind can be represented in terms of these programs.

Encouraged by this success, I began to ponder whether this could be related to the most important scientific question — the physical theory of everything.

First, this approach did not seem too promising - if only because the models I studied (cellular automata) seemed to work in such a way that it completely contradicted everything I knew from physics. But somewhere in the 88th year - at the time when the first version of Mathematica was released , I began to understand that if I changed my ideas about space and time, perhaps this would lead me to something.

Simple theory of everything?

From the article it does not at all seem obvious that the theory of everything for our universe should be simple. Indeed, the history of physics introduces additional doubts, because the more we learn, the more complex things appear, in any case, in terms of the mathematical apparatus introduced by them. But, as noted, for example, by theologians many centuries ago, there is an obvious feature of our universe — there is order in it. Particles of our universe are not only subject to some of their laws, but also obey a certain set of general laws.

But how simple can the theory of everything be for our Universe? Let's say we can present it as a program, say, in the Wolfram Language . How big will this program be? Will it be comparable to the length of the human genome, or more like the operating system in terms of volume? Or will it be significantly less?

If I had answered this question before I began to explore the computational universe of simple programs, I would most likely have answered that such a program must be something very complicated. However, I was able to find that in the computational universe, even extremely simple programs can demonstrate arbitrarily complex behavior (this fact is reflected in the general principle of computational equivalence ).

Universe data structure

But what should such a program be? One thing is clear : if a program can indeed be extremely simple, then it will be too small to explicitly encode some obvious features of our Universe, such as particle masses, various kinds of symmetry, or even spatial dimensionality. All of these things must emerge in some way from something lower and fundamental.

But if the behavior of the universe is determined by a simple program, then what is the data structure with which this program works? At first I suggested that it should be something simple to describe, like, for example, the structure of cells that appears in the cellular automaton. But even if such a structure works well for describing models of various things , it seems that it should be very implausible for fundamental physical models. Yes, you can find such rules that will demonstrate behavior that on a large scale will not show the obvious properties of the structure. However, if physics can indeed be described by some simple model, then it seems that such a rigid structure for space cannot be included in it, and that the properties of space must flow from something.

So what is the alternative? We will need a lower level concept than the space from which it will be born. We also need a basic data structure that is as flexible as possible. I have been thinking about this for many years, studying a wide variety of computational and mathematical formal systems. But in the end I realized that in fact everything that I came across can be represented in one way - through networks.

A network — it’s a graph — consists of a number of nodes that are connected by connections. And all the properties of the graph follow from the structure of these links.

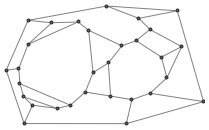
Space as a graph

So can space consist of something like that ? In classical physics and GR, space is not represented as consisting of anything. It is presented in the form of some mathematical construction, which serves as something like a scene on which there is a continuous range of possible positions occupied by different objects.

But can we say for sure that space is continuous? When quantum mechanics began, the idea that space, like everything else, was quantized was popular . But it was not clear how this idea can be mated with the SRT, in fact, there was no clear evidence of the discreteness of space. When I started to study physics in the seventies, the discussion of space discreteness came to naught, plus it was experimentally proved that at scales up to 10 ^-18 m (1/1000 of the proton radius, or attometer ), discreteness is not observed. After 40 years and tens of billions of dollars spent on particle accelerators, on a scale of up to 10 ^-22 m (or 100 yoktometers ), the discreteness of space was not found.

However, it is believed that it should appear on a scale of about Planck length - 10 ^-34 meters. But when people think about it , say, in the context of spin networks, loop gravity, or whatever you are, they tend to assume that everything that happens there is closely related to formalisms and concepts of quantum mechanics.

But what if space — probably on a Planck scale — is just a good old graph, devoid of quantum properties? It does not sound particularly impressive, but to set such a graph, much less information is needed - it is enough just to say which nodes are connected to which.

But how can this generate space? First of all, where does the apparent continuity of space appear on a large scale? In fact, everything is very simple: it can be the result of a large number of nodes and connections. A bit like what happens in liquids — say, in water. On a small scale, we can observe molecules scattering in thermal motion. However, the scale effect causes all of these molecules to produce what we perceive as a continuous fluid.

It so happened that in the mid-80s I spent a lot of time studying this phenomenon - it was part of my work, in which I understood the nature of the seemingly randomness of turbulent fluid flows . In particular, I was able to show that if we represent molecules as cells of a cellular automaton, then their large-scale behavior will be accurately described by differential equations for fluid flows.



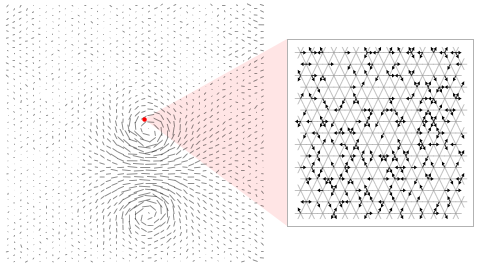
And therefore, when I began to think about the possibility of the existence of a substructure of space, which can be represented as a network, I thought that the same methods could be used here, and that this could reduce Einstein’s GTR equations to other, much lower levels.

Maybe there is nothing but space

Good. Suppose space is a network. But what about all things in space? What can you say about electrons, quarks, protons and so on? Standard physical concepts suggest that space is a scene on which particles, strings or whatever is located. However, this view becomes very complex. But there is a simpler option: perhaps everything in our universe consists of space.

In the last years of his life, Einstein was very passionate about this idea . He believed that, perhaps, such particles as electrons can be considered as something like black holes that consist of only one space. However, relying only on the formalism of GR, Einstein could not develop this idea, as a result of which it was abandoned.

And so it was that a hundred years before, similar ideas had been living in the minds of some people. These were times before the SRT, when people thought that the space was filled with a fluid-like medium — ether (ironically, we are now returned to the model of the filled space — the Higgs field , quantum fluctuations in a vacuum, and so on). Meanwhile, it was clear that there are different types of atoms, corresponding to different chemical elements. And it was suggested (in particular, Kelvin ) that different atoms of the ether can be compared to different atoms.



This is an interesting idea, albeit a wrong one. But, representing space as a network, we can consider a similar idea: perhaps the particles correspond to certain structures of the network . Perhaps everything in the universe is a network, and matter corresponds to some structure of this network. Such things can easily be found on the field of the cellular automaton. Even if each cell obeys some simple rules, certain structures with their properties appear in the system - just like particles with the physics of interaction with each other.



How all this can be implemented on networks is a separate and very big topic. However, we should first discuss one very important thing - time.

What is time?

In the 19th century there were concepts of space and time. Both were described by coordinates, and with the help of some mathematical formalisms appeared in a similar way. However, the idea that space and time are one and the same in some way was not the case. But then Einstein appeared with GTR, and people began to talk about space-time , in which space and time are the faces of some kind of a single concept.

It introduces a lot of meanings to the SRT, in which, for example, moving with variable speed is the essence of rotation in four-dimensional space-time. And all this century, physicists have considered space-time as a kind of entity in which space and time do not have fundamental differences.

But how will all this work in the context of the network space model? Of course, you can enter a four-dimensional network in which time will work the same way as space. And then just say that our universe corresponds to a certain space-time network (or a family of networks). Each network must be determined by some restrictions: our universe has such and such properties, and it turns out that it satisfies such and such equations. However, this seems to be a non-constructive approach — it doesn’t talk about how the universe behaves, but only that if something has this kind of behavior, then it can be something of the universe.

And, for example, in the context of programs, space and time appear very differently. In cellular automata, for example, cells are located in space, but the behavior of the system occurs in incremental changes in time. But here is a moment: from the fact that low-level rules strongly delimit the behavior of space and time, it does not follow that on a large scale they will not behave in a similar way - as it should be in modern physics.

Network formation

So let's assume that a network is a subspace structure. How is this network formed ? You can enter a simple hypothesis, which is that there is some local rule that says that if you see some fragment of the network that looks in some way, then it should be replaced with a fragment that looks like this.



But now things are getting a little more complicated. After all, there may be many places on the network where you can apply this rule. So what determines the order of processing each fragment?

In fact, every possible ordering corresponds to its own time stream. And one could imagine a theory in which all flows take place, and our universe has a multiple history .

But we can do without this hypothesis. Instead, it is quite possible that there is only one thread of time - and this correlates well with what we know about the world, with our experience. And in order to understand this, we should do something similar to what Einstein did, when formulating the SRT: we should introduce a more realistic model of what an observer can be.

Needless to say, any real observer should be able to exist in our universe. Thus, if the universe is a network, then the observer must be some part of this network. Recall now the constant small changes that occur in the network. To know that a similar change (update) has occurred, the observer himself must be changed (updated).

If you go through this whole chain of thought that I’ve spent in the A New Kind of Science (NKS) book, you’ll understand that the only thing that observers in the history of the universe can see is a causal network, when one event causes another.

And then it turns out that there is a certain class of basic rules for which different orders of basic updates do not affect the cause-effect network. I call them the "causally invariant" rules.

Causal invariance is an interesting property that has analogues in various computational and mathematical systems, for example, that transformations in algebra can be applied in any order and will give the same final result. But in the context of the universe, its consequence is that it ensures that there is only one time flow in the universe.

Conclusion STO

So what about space-time and SRT? Here, as I understood in the mid-90s, something exciting is happening: if there is causal invariance, then it follows from this that, on a large scale, SRT will appear by itself. In other words, even if at the lowest level of space and time, everything happens quite differently, then on a larger scale, all this gives rise to what SRT prescribes.

Roughly speaking, the reference systems in the special theory of relativity — associated, for example, with movements at different speeds — correspond to different sequences of low-level network changes. But due to causal invariance, the general behavior associated with different sequences is exactly the same — in this way, the system satisfies the principles of STR.

At the beginning, this situation might seem hopeless: how can a network, which treats space and time in different ways, converge with the SRT? But it works. And, in fact, I do not know of any other model that can successfully deduce the principles of SRT from something lower level; in modern physics it has always been presented as a given.

Conclusion of GR (General Relativity)

OK, SRT can be obtained from simple models based on networks. But what about GR? There is a very good news: based on various assumptions, in the late 90s I managed to derive Einstein's equations from the dynamics of networks.

This whole story is actually somewhat more complicated, but here’s a rough retelling. First, we need to imagine how the network creates space from itself. It should be remembered that the network is only a set of nodes and connections. Moreover, the nodes can be located in one-dimensional, two-dimensional, or any n-dimensional space.

It is easy to see that there are networks that on a large scale appear to be two-dimensional or three-dimensional. In fact, there is a simple test for determining the effective dimension of a network. Take a node, and then look at all the nodes that are at a distance from r links. If the network manifests itself as d- dimensional, then the number of nodes in this “sphere” will be about r ^d .



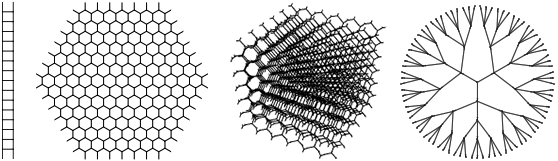
And here things get an interesting turn. If the network behaves like a d- dimensional space undistorted in a space of higher dimension, then the number of nodes will always be around r ^d . But if the behavior is like a curved space (as in GTR), then a correction term will take place proportional to such a mathematical object as the Ricci tensor . And this is very interesting, because the Ricci tensor just appears in the Einstein equations.



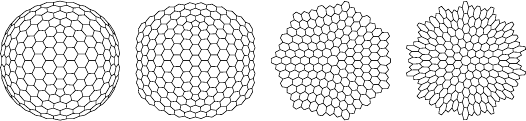
There are many mathematical difficulties. Consider the shortest paths - geodetic network lines. It should be understood how to do anything, not only in space, but also on the network over time. You should also understand the extent to which the properties of the network appear.

When deriving mathematical results, it is important to be able to obtain various kinds of average values. In essence, this is similar to the derivation of equations for a fluid from the dynamics of molecules: you must be able to take an average of a certain range of random values ​​in low-level interactions.

But the good news is that there are an immense number of systems built even on extremely simple rules that are similar to the digits of pi , that is, for any application, they are quite random . It turns out that even if the features of the causal network are fully defined for the one who knows the initial state of the network, then most of these features will be, in fact, random.

That's what we have in the end. If we introduce the assumption of effective microscopic randomness and assume that the behavior of the system as a whole does not lead to a change in all the limiting dimensions, it follows from this that the scale behavior of the system satisfies the Einstein equations !

I guess this is very interesting. Einstein's equations can be obtained from almost nothing. This means that these simple networks reproduce the features of gravity that we know from modern physics.

There are a number of details that do not fit the format of this article. I voiced many of them for quite some time in NKS , especially in the notes at the end.

Some of the things may be worth mentioning. First, it is worth noting that these basic networks are not only represented in the usual continuously defined space, but also do not define such topological concepts as inside and outside. All these concepts are a consequence and are derived.

When it comes to the derivation of the Einstein equations, Ricci tensors are born from geodesic lines on the network along with the growth of spheres, which originate from each point on the geodesic line.

The resulting Einstein equations are Einstein equations for a vacuum. But as in the case of gravitational waves, one can effectively separate the features of space associated with matter, and then obtain the full Einstein equations in terms of matter-energy-momentum.

When I write this, I understand how easy it is to slip into the “language of physicists” (probably, this is due to the fact that I was engaged in physics in my youth ...). But simply enough to say that at a high level there is an exciting thing, which is that the equations of general relativity can be derived from a simple idea about networks and cause-and-effect invariant replacement rules. Having made surprisingly little, we get a bright star of physics of the 20th century: the general theory of relativity.

Particles, quantum mechanics, etc.

It is very cool to be able to withdraw GR. But this physics does not end there. Another very important part of it is quantum mechanics . I'm afraid I won't be able to expand this topic in detail in this article, but apparently such particles as electrons, quarks, or Higgs bosons should appear in the form of some particular areas of the network. In a qualitative sense, they may not differ much from Kelvin's “essential knots”.

But then their behavior must follow the rules that we know from quantum mechanics — or, more specifically, from quantum field theory. A key feature of quantum mechanics is that it can be formulated in terms of multiple behaviors, each of which is associated with a specific quantum amplitude. I did not fully understand all this, but there is a hint that something like this happens if you look at the evolution of the network with various possible sequences of low-level substitutions.

My network model, strictly speaking, has no quantum amplitudes. It is more similar (but not exactly) to the classical, in fact, probabilistic model. And for half a century, people believed that practically unsolvable problems were associated with such models. After all, there is Bell's theorem, which says that if there is no instant non-local dissemination of information, then there is no such model of “hidden variables” that can reproduce the quantum-mechanical results observed experimentally.

But there are fundamental observations. It is quite clear what the nonlocality means in the ordinary space of some dimension. But what can be said in the context of networks? It's all different. Because everything is determined only by connections. And even though the network may on a large scale appear three-dimensional, the possibility remains that there are certain “threads” connecting some areas that would be separated from each other without them. And one thought haunts me - there is reason to believe that these threads can be generated by particles like structures propagating in a network.

In search of the universe

Well, it turns out that some network-based models can reproduce the models of modern physics. But what should start the search for a model that exactly reproduces our universe?

My first thought is to start with the existing physics and try to adapt the engineering and application rules to reproduce it. But is this the only way? And what if you just start listing all possible rules, looking for among them those that will describe our universe?

Without starting to study the computational universe of the simplest programs, I would think that this is a crazy undertaking: the rules of our universe cannot be simple enough to be found by simple enumeration. But when I saw what was going on in the computational universe and saw some other examples in which tremendous things were found by brute force, I realized that I was mistaken.

But what will happen if someone really starts a similar search ? Here is a selection of networks obtained after a rather small number of steps, using all the possible rules of a certain, very simple type:



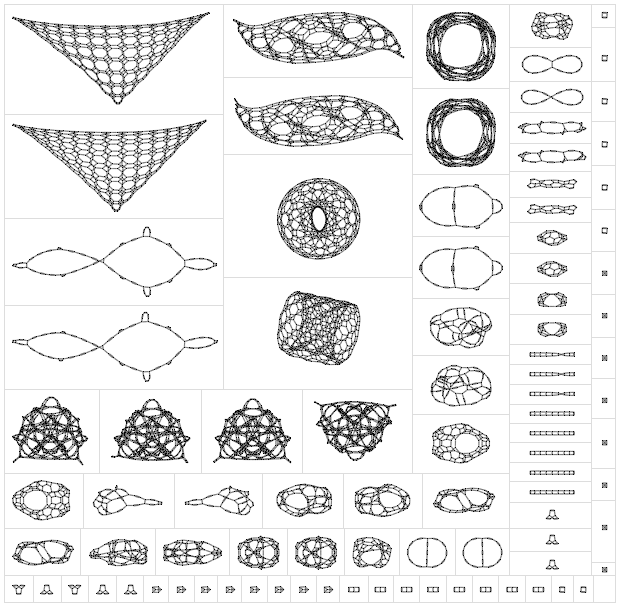
Some of these networks are clearly not consistent with our universe. They just froze after several iterations, that is, the time in them, in fact, stopped. Or the structure of their space was too simple. Or they had an infinite number of dimensions. Or some other problems.

It's great that with such amazing speed we can find those rules that clearly do not correspond to our universe. And to say that this object is our universe is a much more difficult task. Because even if you simulate a large number of steps, it will be incredibly difficult to show that the behavior of this system demonstrates the same thing that the physical laws tell us about the early moments of the life of the universe.

Although there are a number of encouraging things. For example, these universes can be born with a virtually infinite number of dimensions, and then gradually shrink to a finite number of dimensions, potentially eliminating the need for overt inflation in the early Universe.

And if you talk at a higher level, you should remember that if you use very simple models, then there will be a large distance between "neighboring models", so most likely, these models will either accurately reproduce known physical constructions, or they will be far from the truth.

In the end, you need to reproduce not only the rules, but also the initial state of the universe. And as soon as we recognize it, we will be able in principle to know the exact evolution of the universe. So does this mean that you could immediately know everything about the universe? Definitely not. Because of a phenomenon that I call “computational irreducibility,” which implies that if you know the rules and the initial state for a system, it can still require an irreducible amount of computational work to track each step of the system to find out what it is doing.

However, there is a chance that someone will be able to find a simple rule and an initial state, saying: “ Look, this is our universe! ” We would find our universe in the space of all possible universes.

Of course, this would be a significant day for science.

But many other questions would arise. , ? , , ?

, , , , . , , , , — , , -.

,

. , , .

, . ? , , - 99- — A New Kind of Science . , , , .



, 2002 , . , , . : , .

, , . . . , , .

, , , , .



- , . . , . A New Kind of Science , , .

2005 , , . Wolfram|Alpha . Wolfram|Alpha , , — , , , Wolfram Language , .

—

. , , , 2005 .

? . , .

, . , , , . , . , , .

, , , . : , . , ( ). , .

, . . , , , . , , , - , .

- , , , , , . , , . , , , , , . , . , , , , , , .

, . .

— : " ! " , , , , , .

: " ? " « , , , , , ? - , - ?»

— , . -, " ! " " , ".

, , , 90 . , . . , , - , .

: " , , , , ". , , . , , , . , - , , — , .

What is needed?

, , , ? , , .

— , , , , (, , A New Kind of Science ).

, , , . , . , , , , .

, /. . , , , , , . , .

, , , , , . , , . . , , , .

— , , , . , , , . . , , , , , .

?

? , , . . .

. , , . : , , , , , — .

, 100 , , (« ») , . , , — . , , , .

— , , . — , . , . , , , - .