Solving square equations through derivatives

Hello, dear readers. After reading the article, you will probably have a logical question: “Why, in fact, is it necessary?”. By virtue of this, at first I consider it necessary to inform in advance that the desired method of solving quadratic equations is presented rather from the moral and aesthetic side of mathematics, rather than from practical dry application. I also apologize in advance to those readers who find my amateurish sayings unacceptable. So, let's start hammering nails with a microscope .

We have an algebraic equation of the second degree (it’s also square) in general:
')


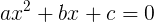
Let's move from a quadratic equation to a quadratic function:



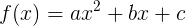
Where, obviously, you need to find such argument values 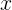functions in which it would return zero.

It seems you just need to solve a quadratic equation using the Viet theorem or through a discriminant . But we have not gathered here for this. Let's better get the derivative!



Based on the definition of the physical meaning of a derivative of the first order, it is clear that substituting the argument 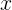in the function obtained above, we (in particular) obtain the rate of change of the function at the point given by this argument.

What to do next? Unclear. And in any incomprehensible case, you need to take the derivative again:



This time we got the “speed of speed” of the change in function (I mean acceleration ) at a specific point. After a little analysis of the result, we can conclude that the “acceleration” is a constant that does not depend on the argument of the function - remember this.

Now let's remember a little physics and uniformly accelerated motion (RUD). What do we have in the arsenal? True, there is a formula for determining the coordinate of the displacement along the axis at the desired motion: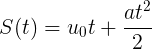



Where - time 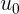- starting speed, 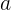- acceleration.
It is easy to see that our original function is just a throttle.


Now it remains to understand what is what, and what we lack.

"Acceleration" 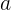we already have - it is a second order derivative 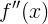derived above. But to get the initial speed 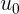, we need to take in general any 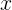(denote it as 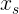) and substitute it into the derivative now of the first order - for it will be the desired.

In this case, the question arises, what 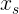have to take? Obviously, such that the initial speed 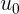was equal to zero, so that the formula of “displacement at ORE” began to look like:



In this case, we make an equation for the search :

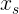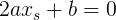[framed 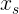first order derivative ]

The root of such an equation is relatively 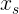will be:



And the value of the original function with this argument will be:



Recall what purpose we set ourselves at the very beginning: “it is necessary to find such argument values 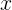functions in which it would return zero. " In other words, our position need to "reach zero".

Since we now know the initial speed, acceleration, and which path to go, it is time to note the following:

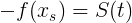, as well as

Then, substituting all known values, we get:



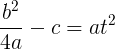
Let's divide everything by :



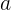Now it becomes obvious that:



Connect all the “puzzle details” together:



So we got the final solution of the task. In general, we did not discover America - we simply came to the formula for solving a quadratic equation through a discriminant in a roundabout way. It does not carry practical sense (in much the same way, one can solve the first / second degree equations of any (not necessarily general) form).

The purpose of this article is, in particular, the heating of interest in the analysis of the mat. functions and in general to mathematics.

Peter was with you, thank you for your attention!