2-3-tree. Naive implementation
 Recently, I needed to write a 2-3-tree and I began to look for information on the Russian-language Internet. Unfortunately, neither on Habré, nor on other resources, I could not find enough complete information in Russian. All resources had the same thing: tree properties, how keys are inserted into a tree, search in a tree and sometimes a simple example of how a key is removed from a tree; there was no implementation.
Recently, I needed to write a 2-3-tree and I began to look for information on the Russian-language Internet. Unfortunately, neither on Habré, nor on other resources, I could not find enough complete information in Russian. All resources had the same thing: tree properties, how keys are inserted into a tree, search in a tree and sometimes a simple example of how a key is removed from a tree; there was no implementation.Therefore, after I did what I needed, I decided to write this article. I think someone will be useful for educational purposes, since in practice they usually implement the equivalent of 2-3- and 2-3-4-trees - red-ebony .
Prologue
Those who know what a binary search tree and its shortcomings can go further are nothing new here.
Most programmers (and not only) know such a tree as a binary search tree . This tree has very simple properties:
')
- Both subtrees — left and right — are binary search trees.
- All nodes of the left subtree of an arbitrary node X have data key values less than the data key value of the node X itself.
- At the same time, the data key values of all nodes of the right subtree (of the same node X) are equal to or larger than the data key value of the node X.
Search trees are used when you need to perform a search operation very often. In the usual search tree there is a very big drawback: when we get sorted data as input, our tree becomes a regular array:
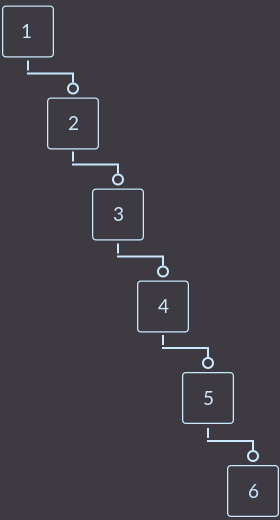
And then the search operation will be carried out for the same complexity as in the array, - for O (n), where n is the number of elements in the array.
There are several ways to make a normal tree balanced (search has O (log n) complexity). This is very well written in two articles from the nickme habrauser : randomized search trees and AVL-trees .
General properties of 2-3 trees
Definition from wiki:
2-3-tree is a data structure, which is a B-tree of Degree 1, whose pages can contain only 2 vertices (vertices with one field and 2 children) and 3 vertices (vertices with 2 fields and 3 children). Leaf vertices are an exception - they have no children (but there can be one or two fields). The 2-3 trees are balanced, that is, each left, right, and central subtree has the same height, and thus contains equal (or almost equal) amounts of data.
Properties:
- All non-leaf vertices contain one field and 2 subtrees or 2 fields and 3 subtrees.
- All leaf vertices are at the same level (at the lower level) and contain 1 or 2 fields.
- All data is sorted (according to the binary search tree principle).
- Leafy vertices contain one or two fields indicating the range of values in their subtrees. The value of the first field is strictly greater than the largest value in the left subtree and less than or equal to the smallest value in the right subtree (or in the central subtree if it is 3-vertex); similarly, the value of the second field (if any) is strictly greater than the largest value in the central subtree and less than or equal to the smallest value in the right subtree. These non-leaf vertices are used to direct the search function to the desired subtree and, ultimately, to the desired sheet. This property will not be executed if we have the same keys. Therefore, it is possible that equal keys are in the left and right subtrees at the same time, then the key in the non-leaf vertex will coincide with these keys. This does not affect the correctness of the work and algorithm performance. ).
2-3 tree example:
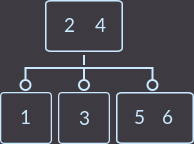
For simplicity, we will use different keys.
Tree view in code
I will write on the so-called “C with classes”, as I myself am a C programmer, but I am madly in love with such things in C ++ as constructors, the presence of class member methods and friendly functions.
The vertices of our tree will be represented as 4-vertices (this is when a vertex can have 3 keys and 4 sons). This solution was chosen for several reasons: firstly, it is easier to make a naive (direct) implementation, and secondly, the code is so strongly framed with if and this solution has reduced the number of checks and simplified code.
This is how the vertex view looks like:
Class for a 2-3 tree vertex
struct node { private: int size; // int key[3]; node *first; // *first <= key[0]; node *second; // key[0] <= *second < key[1]; node *third; // key[1] <= *third < key[2]; node *fourth; // kye[2] <= *fourth. node *parent; // , bool find(int k) { // true, k , false. for (int i = 0; i < size; ++i) if (key[i] == k) return true; return false; } void swap(int &x, int &y) { int r = x; x = y; y = r; } void sort2(int &x, int &y) { if (x > y) swap(x, y); } void sort3(int &x, int &y, int &z) { if (x > y) swap(x, y); if (x > z) swap(x, z); if (y > z) swap(y, z); } void sort() { // if (size == 1) return; if (size == 2) sort2(key[0], key[1]); if (size == 3) sort3(key[0], key[1], key[2]); } void insert_to_node(int k) { // k ( ) key[size] = k; size++; sort(); } void remove_from_node(int k) { // k ( ) if (size >= 1 && key[0] == k) { key[0] = key[1]; key[1] = key[2]; size--; } else if (size == 2 && key[1] == k) { key[1] = key[2]; size--; } } void become_node2(int k, node *first_, node *second_) { // 2-. key[0] = k; first = first_; second = second_; third = nullptr; fourth = nullptr; parent = nullptr; size = 1; } bool is_leaf() { // ; . return (first == nullptr) && (second == nullptr) && (third == nullptr); } public: // node(int k): size(1), key{k, 0, 0}, first(nullptr), second(nullptr), third(nullptr), fourth(nullptr), parent(nullptr) {} node (int k, node *first_, node *second_, node *third_, node *fourth_, node *parent_): size(1), key{k, 0, 0}, first(first_), second(second_), third(third_), fourth(fourth_), parent(parent_) {} friend node *split(node *item); // ; friend node *insert(node *p, int k); // ; friend node *search(node *p, int k); // ; friend node *search_min(node *p); // ; friend node *merge(node *leaf); // ; friend node *redistribute(node *leaf); // ; friend node *fix(node *leaf); // ( merge redistribute) friend node *remove(node *p, int k); // , ; }; Insert
In order to insert an element with the key key into the tree, you need to act according to the algorithm:
- If the tree is empty, then create a new vertex, insert the key and return this vertex as the root, otherwise
- If the vertex is a leaf, then we insert the key into this vertex and if we have received 3 keys at the vertex, then we divide it, otherwise
- Compare the key key with the first key at the top, and if the key is less than the given key, then go to the first subtree and go to step 2, otherwise
- We look, if a vertex contains only 1 key (is a 2-vertex), then go to the right subtree and go to step 2, otherwise
- Compare the key key with the second key at the vertex, and if the key is less than the second key, then go to the middle subtree and go to step 2, otherwise
- Go to the right subtree and go to step 2.
For example, insert keys = {1, 2, 3, 4, 5, 6, 7}:
When inserting key = 1, we have an empty tree, and then we get a single vertex with a single key, key = 1:

Next, insert key = 2:

Now insert key = 3 and get a vertex containing 3 keys:

Since this vertex violates the properties of 2-3-trees, we must deal with this. But let's deal with this division: the key that is in the middle (in our case, key = 2), we move it to the parent node to the appropriate place, or if we have a single node in the tree, then it is the root of the tree, which means we create a new vertex and transfer the middle key key = 2 there, and sort the rest of the keys and make them the sons of the new root:
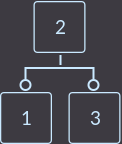
Then we insert the key = 4 according to the algorithm:

Key = 5:
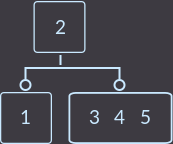
The properties of 2-3 trees are again broken, we make the separation:
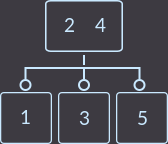
Key = 6:

Key = 7:
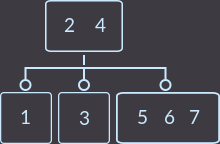
Now we have to make two divisions, because the vertex into which the new key was inserted now has 3 keys (first we divide it):
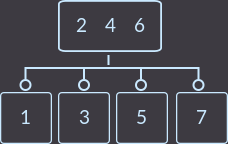
And now the root has 3 vertices - divide it and get a balanced tree, which, with such input data with the usual binary search tree, we could not get:
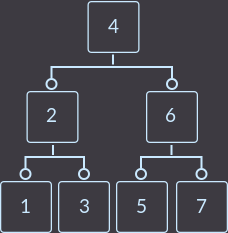
Key insert
node *insert(node *p, int k) { // k p; , .. if (!p) return new node(k); // , 2-3- () if (p->is_leaf()) p->insert_to_node(k); else if (k <= p->key[0]) insert(p->first, k); else if ((p->size == 1) || ((p->size == 2) && k <= p->key[1])) insert(p->second, k); else insert(p->third, k); return split(p); } Split top
node *split(node *item) { if (item->size < 3) return item; node *x = new node(item->key[0], item->first, item->second, nullptr, nullptr, item->parent); // , node *y = new node(item->key[2], item->third, item->fourth, nullptr, nullptr, item->parent); // , . if (x->first) x->first->parent = x; // "" "". if (x->second) x->second->parent = x; // , "" "" "", if (y->first) y->first->parent = y; // . if (y->second) y->second->parent = y; if (item->parent) { item->parent->insert_to_node(item->key[1]); if (item->parent->first == item) item->parent->first = nullptr; else if (item->parent->second == item) item->parent->second = nullptr; else if (item->parent->third == item) item->parent->third = nullptr; // . if (item->parent->first == nullptr) { item->parent->fourth = item->parent->third; item->parent->third = item->parent->second; item->parent->second = y; item->parent->first = x; } else if (item->parent->second == nullptr) { item->parent->fourth = item->parent->third; item->parent->third = y; item->parent->second = x; } else { item->parent->fourth = y; item->parent->third = x; } node *tmp = item->parent; delete item; return tmp; } else { x->parent = item; // , y->parent = item; // "" . item->become_node2(item->key[1], x, y); return item; } } Search
The search is as simple as in a binary search tree:
- We are looking for the desired key key in the current vertex; if we find it, we return the vertex, otherwise
- If key is less than the first key of the vertex, then go to the left subtree and go to step 1, otherwise
- If there is 1 key in the tree, then we go to the right subtree (average if we are guided by our class) and go to step 1, otherwise
- If key is less than the second key of the vertex, then go to the middle subtree and go to step 1, otherwise
- Go to the right subtree and go to step 1.
Key search
node *search(node *p, int k) { // k 2-3 p. if (!p) return nullptr; if (p->find(k)) return p; else if (k < p->key[0]) return search(p->first, k); else if ((p->size == 2) && (k < p->key[1]) || (p->size == 1)) return search(p->second, k); else if (p->size == 2) return search(p->third, k); } Deletion
Deletion in a 2–3 tree, as in any other tree, occurs only from a leaf (from the lowest top). Therefore, when we have found the key to be deleted, we first need to check whether this key is in a leaf or non-leaf vertex. If the key is in a non-leaf vertex, then you need to find an equivalent key for the key being removed from the leaf vertex and swap them. There are two options for finding the equivalent key: either find the maximum element in the left subtree, or find the minimum element in the right subtree. Let's choose the second option, as I like it more. For example:

To remove the key = 4 from the tree, first we need to find the equivalent emu element and swap them: this is either key = 3 or key = 5. Since I selected the second method, I change the keys key = 4 and key = 5 in places and delete key = 4 from the sheet (“dash” will indicate the location of the key that we deleted):
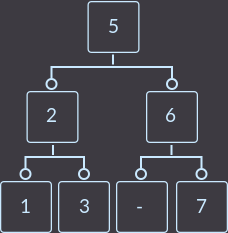
Minimum Key Search
node *search_min(node *p) { // 2-3- p. if (!p) return p; if (!(p->first)) return p; else return search_min(p->first); } Key removal
node *remove(node *p, int k) { // k 2-3- p. node *item = search(p, k); // , k if (!item) return p; node *min = nullptr; if (item->key[0] == k) min = search_min(item->second); // else min = search_min(item->third); if (min) { // int &z = (k == item->key[0] ? item->key[0] : item->key[1]); item->swap(z, min->key[0]); item = min; // , .. min - } item->remove_from_node(k); // return fix(item); // . } After the key has been removed, we can get 4 different situations conceptually: 3 of them violate the properties of the tree, and one does not. Therefore, for the vertex from which the key was deleted, you need to call the fix () fix function, which will return the properties of 2-3 trees. The cases that are described in the function are discussed below.
Repair the tree after removing the key
node *fix(node *leaf) { if (leaf->size == 0 && leaf->parent == nullptr) { // 0, delete leaf; return nullptr; } if (leaf->size != 0) { // 1, , , if (leaf->parent) return fix(leaf->parent); else return leaf; } node *parent = leaf->parent; if (parent->first->size == 2 || parent->second->size == 2 || parent->size == 2) leaf = redistribute(leaf); // 2, else if (parent->size == 2 && parent->third->size == 2) leaf = redistribute(leaf); // else leaf = merge(leaf); // 3, return fix(leaf); } We now turn to possible options that may appear after removing the key. For simplicity, we will consider cases where the depth of the tree is 2. The general case is a tree with a depth of three. Then it will be clear how to cope with the removal of the key in the tree with any depth. What we will do in the final example for most situations. In the meantime, proceed to the special cases.
Case 0:
The simplest case, as well as the following, for which one sentence is enough to understand: if a tree consists of one vertex (root), which has 1 key, then simply delete this vertex. The end.
Case 1:
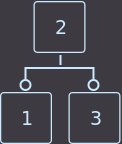
If you want to remove the key from the sheet where the two keys are located, then we simply delete the key and this completes the delete function.
Remove key = 4:
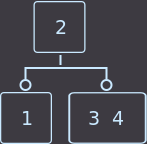 ->
-> 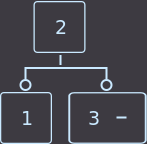 ->
-> 
Case 2 (distribution or redistribute ):
We remove the key from the vertex and the vertex becomes empty. If at least one of the brothers has 2 keys, then we make a simple correct distribution and the work is completed. By the correct distribution, I mean that when cycling the keys between the parent and the sons, the grandchildren of the parent will also need to be moved. You can redistribute the keys from any brother, but it is most convenient from the neighbor, which has 2 keys, while we cyclically shift all the keys, for example, from the example below, remove key = 1:
 ->
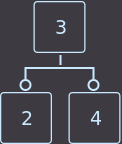
-> 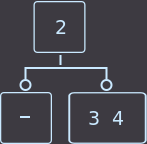 ->
-> 
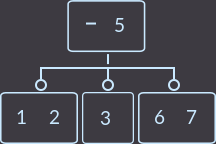
Or here's a second example: our parent has 2 keys, respectively, 3 sons, and we will delete key = 4. Redistribution in our example can be done both from the left brother and from the right one; I chose from the left:
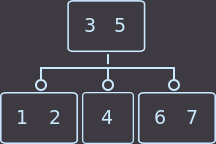 ->
-> 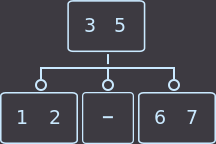 ->
->  ->
-> 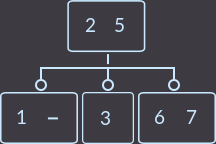 ->
->->

As you can see, the properties of the tree saved.
Redistribution
node *redistribute(node *leaf) { node *parent = leaf->parent; node *first = parent->first; node *second = parent->second; node *third = parent->third; if ((parent->size == 2) && (first->size < 2) && (second->size < 2) && (third->size < 2)) { if (first == leaf) { parent->first = parent->second; parent->second = parent->third; parent->third = nullptr; parent->first->insert_to_node(parent->key[0]); parent->first->third = parent->first->second; parent->first->second = parent->first->first; if (leaf->first != nullptr) parent->first->first = leaf->first; else if (leaf->second != nullptr) parent->first->first = leaf->second; if (parent->first->first != nullptr) parent->first->first->parent = parent->first; parent->remove_from_node(parent->key[0]); delete first; } else if (second == leaf) { first->insert_to_node(parent->key[0]); parent->remove_from_node(parent->key[0]); if (leaf->first != nullptr) first->third = leaf->first; else if (leaf->second != nullptr) first->third = leaf->second; if (first->third != nullptr) first->third->parent = first; parent->second = parent->third; parent->third = nullptr; delete second; } else if (third == leaf) { second->insert_to_node(parent->key[1]); parent->third = nullptr; parent->remove_from_node(parent->key[1]); if (leaf->first != nullptr) second->third = leaf->first; else if (leaf->second != nullptr) second->third = leaf->second; if (second->third != nullptr) second->third->parent = second; delete third; } } else if ((parent->size == 2) && ((first->size == 2) || (second->size == 2) || (third->size == 2))) { if (third == leaf) { if (leaf->first != nullptr) { leaf->second = leaf->first; leaf->first = nullptr; } leaf->insert_to_node(parent->key[1]); if (second->size == 2) { parent->key[1] = second->key[1]; second->remove_from_node(second->key[1]); leaf->first = second->third; second->third = nullptr; if (leaf->first != nullptr) leaf->first->parent = leaf; } else if (first->size == 2) { parent->key[1] = second->key[0]; leaf->first = second->second; second->second = second->first; if (leaf->first != nullptr) leaf->first->parent = leaf; second->key[0] = parent->key[0]; parent->key[0] = first->key[1]; first->remove_from_node(first->key[1]); second->first = first->third; if (second->first != nullptr) second->first->parent = second; first->third = nullptr; } } else if (second == leaf) { if (third->size == 2) { if (leaf->first == nullptr) { leaf->first = leaf->second; leaf->second = nullptr; } second->insert_to_node(parent->key[1]); parent->key[1] = third->key[0]; third->remove_from_node(third->key[0]); second->second = third->first; if (second->second != nullptr) second->second->parent = second; third->first = third->second; third->second = third->third; third->third = nullptr; } else if (first->size == 2) { if (leaf->second == nullptr) { leaf->second = leaf->first; leaf->first = nullptr; } second->insert_to_node(parent->key[0]); parent->key[0] = first->key[1]; first->remove_from_node(first->key[1]); second->first = first->third; if (second->first != nullptr) second->first->parent = second; first->third = nullptr; } } else if (first == leaf) { if (leaf->first == nullptr) { leaf->first = leaf->second; leaf->second = nullptr; } first->insert_to_node(parent->key[0]); if (second->size == 2) { parent->key[0] = second->key[0]; second->remove_from_node(second->key[0]); first->second = second->first; if (first->second != nullptr) first->second->parent = first; second->first = second->second; second->second = second->third; second->third = nullptr; } else if (third->size == 2) { parent->key[0] = second->key[0]; second->key[0] = parent->key[1]; parent->key[1] = third->key[0]; third->remove_from_node(third->key[0]); first->second = second->first; if (first->second != nullptr) first->second->parent = first; second->first = second->second; second->second = third->first; if (second->second != nullptr) second->second->parent = second; third->first = third->second; third->second = third->third; third->third = nullptr; } } } else if (parent->size == 1) { leaf->insert_to_node(parent->key[0]); if (first == leaf && second->size == 2) { parent->key[0] = second->key[0]; second->remove_from_node(second->key[0]); if (leaf->first == nullptr) leaf->first = leaf->second; leaf->second = second->first; second->first = second->second; second->second = second->third; second->third = nullptr; if (leaf->second != nullptr) leaf->second->parent = leaf; } else if (second == leaf && first->size == 2) { parent->key[0] = first->key[1]; first->remove_from_node(first->key[1]); if (leaf->second == nullptr) leaf->second = leaf->first; leaf->first = first->third; first->third = nullptr; if (leaf->first != nullptr) leaf->first->parent = leaf; } } return parent; } Case 3 (bonding or merge ):
Perhaps the most difficult case, since after gluing it is always necessary to go up the tree and again apply operations either merge or redistribute . After redistribute, the algorithm for restoring 2-3-tree properties after deleting a key can be terminated, since the vertices in this operation are not deleted.
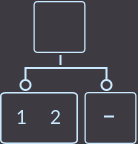
First, let's see how to remove key = 3 from a node whose parent has only two sons (~ 1 key):
 ->
->  ->
->  ->
-> 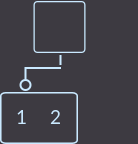 ->
-> 
What have we done? We removed the key key = 3. Then we need to transfer the key from the parent to the son where the key is: in this case, the left son. Then you need to remove the vertex from which the key was removed. And the last step is to check if the parent was the root of the tree, then delete this root and assign the new root to the vertex where we transferred the key, otherwise you will have to call the fix () fix function for the parent. It looks easy.
Now consider two options when the parent has 2 keys. In the first variant, remove key = 3 (from the middle son):
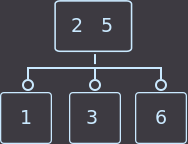 ->
-> 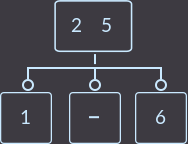 ->
-> 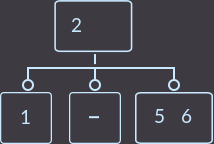 ->
-> 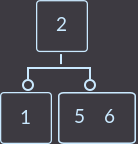
What have we done this time? We again transferred the key of the parent (already one of the two) to the son and removed the son who does not have the keys. Since the parent had 2 keys, it is not necessary to check whether the parent was a root. In the case described above, the correction algorithm is as follows: you need to transfer a smaller parent key to a subtree with smaller keys or a larger key to a subtree with larger keys, and delete the top without keys. Another example, remove key = 1:
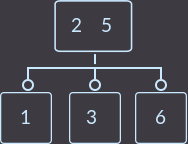 ->
-> 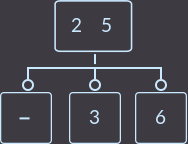 ->
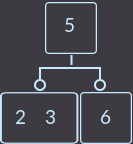
-> 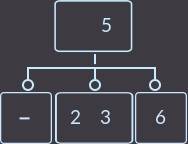 ->
-> 
Gluing
node *merge(node *leaf) { node *parent = leaf->parent; if (parent->first == leaf) { parent->second->insert_to_node(parent->key[0]); parent->second->third = parent->second->second; parent->second->second = parent->second->first; if (leaf->first != nullptr) parent->second->first = leaf->first; else if (leaf->second != nullptr) parent->second->first = leaf->second; if (parent->second->first != nullptr) parent->second->first->parent = parent->second; parent->remove_from_node(parent->key[0]); delete parent->first; parent->first = nullptr; } else if (parent->second == leaf) { parent->first->insert_to_node(parent->key[0]); if (leaf->first != nullptr) parent->first->third = leaf->first; else if (leaf->second != nullptr) parent->first->third = leaf->second; if (parent->first->third != nullptr) parent->first->third->parent = parent->first; parent->remove_from_node(parent->key[0]); delete parent->second; parent->second = nullptr; } if (parent->parent == nullptr) { node *tmp = nullptr; if (parent->first != nullptr) tmp = parent->first; else tmp = parent->second; tmp->parent = nullptr; delete parent; return tmp; } return parent; } ! Important! When gluing or redistributing a non-leaf top, you will also need to glue and / or redistribute the sons of the brothers.
Final example of deleting keys:
I picked an example so that you can see all the main cases (except for case 0 ). First, insert the keys keys = {10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 5, 15, 25, 8} into an empty tree and get :
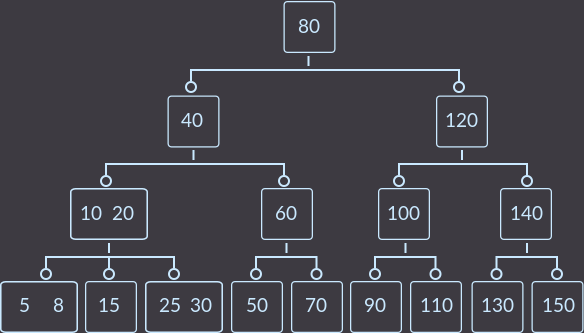
Now we will delete in order the keys keys = {5, 8, 10, 30, 15}.
After removing key = 5, we get:
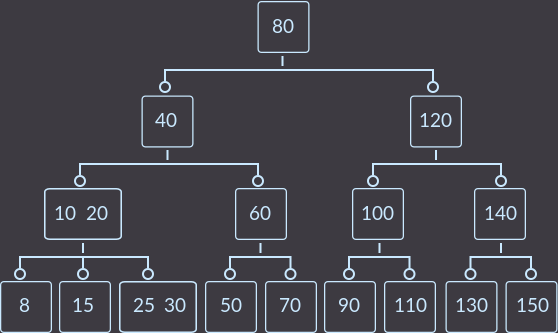
Delete key = 8:
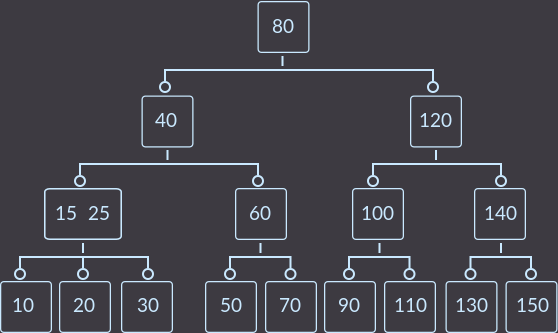
Now key = 10:
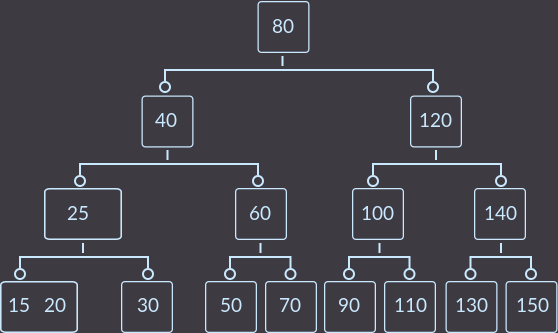
Key = 30:
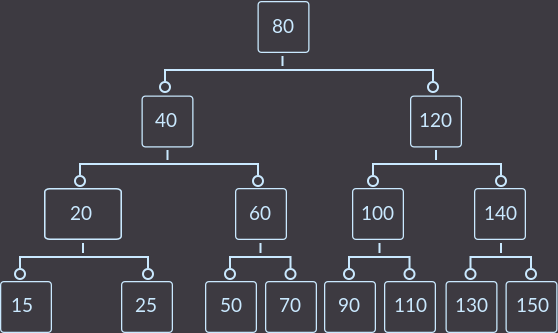
And finally, key = 15. Since this is where the merge operation occurs when the tree is corrected, we will look at all the steps.
Step 1. View the tree immediately after the first call to fix ():
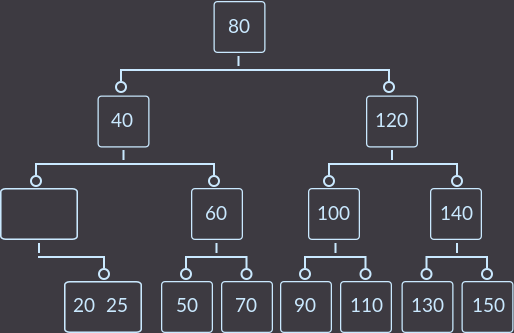
Step 2. Second fix () call:
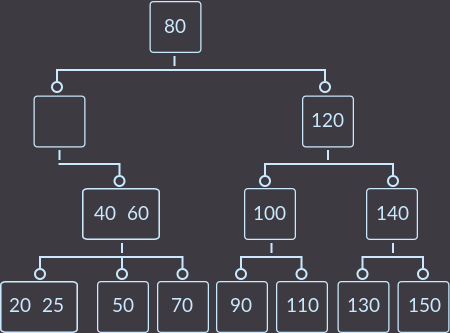
Step 3. Third fix () call:
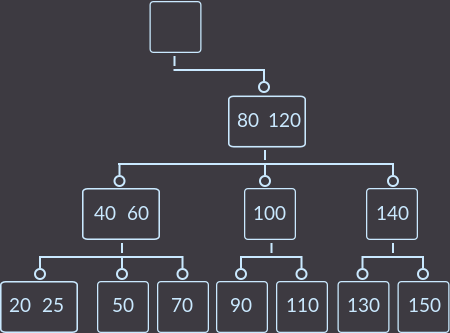
Step 4. Last fix () call:
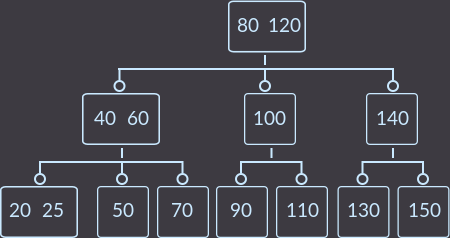
This is how we removed the key key = 15 and the tree was left with the properties it should be with.
That's all, thank you for your attention.
Source: https://habr.com/ru/post/303374/
All Articles