Generating passwords for Road Rash 1 and 2 games
Recently, I saw a post about Road Rash on Habrahabr and I wondered: “How does the password system work in two other parts?”. I would like to share my observations and results with you in this article.

The password consists of 20 positions, each position consists of 5 bits, a total of 20 * 5 = 100 bits. These bits save game data parameters:
Now let's see what the raw password consists of:
(U, SN, SN, SN, SN) (U, PC, PC, PC, PC) (U, RF, RF, RF, RF) (U, PD, PD, PD, PD) (U, GV, GV , GV, GV) (H, H, H, H, H) (H, H, H, H, H) (H, H, H, H, H) (H, H, H, H, H) ( N, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (U, U, L, L, L) (U, U, B, B, B) (C2, C2, C2, C2, C2) (C3 , C3, C3, C3, C3) (C4, C4, C4, C4, C4)
')
U - unused bits.
SN is the number of the occupied space in Sierra Nevada (0-15) in binary number system.
PC is the number of the occupied space in the Pacific Coast (0-15) in binary number system.
RF is the number of the occupied space in Redwood Forest (0-15) in binary number system.
PD is the number of the occupied place in Palm Desert (0-15) in binary number system.
GV is the number of the occupied place in Grass Valey (0-15) in binary number system.
H - the number of points (0-10485750) in increments = 10. The number of points is divided by 10 and the resulting number is transferred to the binary number system.
N is a bit of negative values.
M - the amount of money ((-83886070) -83886070) with a step = 10.
In order to create a positive amount of money, you need to divide the amount of money by 10 and convert the resulting number into binary number system.
In order to create a negative amount of money, you need:
L is the level number (1-5) in binary number system.
B is the number of the motorcycle (0-7) in binary number system.
C1 = (sum of positions from 1 to 17) mod64 (The resulting number is transferred to the binary number system and mirrored).
C2 = (sum of positions from 6 to 10) mod32.
C3 = (sum of positions 11 through 15) mod32.
C4 = C2 XOR C3.
Characters in the positions can take the values 0-9 and AV. The bits in the positions are encoded in accordance with the fact that 0 = 00000, 1 = 00001, 2 = 00010 ... U = 11110, V = 11111. That is, this is a simple 5 bit encoding.
The password consists of 8 positions, each position consists of 5 bits, a total of 8 * 5 = 40 bits. These bits save game data parameters:
Now let's see what the raw password consists of:
(?, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (U, U, L , L, L) (B, B, B, B, C1) (T, T, T, T, T) (C2, C2, C2, C2, C2)
? - always equal to zero.
U - unused bits.
M - the amount of money (0-327670) with a step = 10. The amount of money is divided by 10 and the resulting number is transferred to the binary number system.
L is the level number (1-5) in binary number system.
B is the number of the motorcycle (0-15) in binary number system.
T - traces passed (0-5).
The order of bits from high to low:
4 - is responsible for passing the fifth route.
3 - is responsible for the passage of the fourth route.
2 - is responsible for passing the third route.
1 - is responsible for the passage of the second route.
0 - is responsible for passing the first track.
C1 = (sum of positions from 1 to 6, not counting the 5 position) mod32 (The resulting number is transferred to the binary number system and mirrored).
C2 = ((sum of positions from 1 to 6) mod32) XOR 7 position.
Coding of values is the same as in the first part.
But that is not all!
I cooked something else ...
Let's digress a bit from the Sega console and move on to Nes (Dandy). This game is very patted my nerves. Who played, he remembers the long questions in Japanese, because of which the passing game turns into hell. Passwords in it are simple, but with a tackle. To complete the game 100% needed to collect 4 armor. But there is one problem, to get them, you had to answer a ton of questions. No matter how much I rummaged on the Internet and in my book of codes, I never found the passwords that save the collected armor. And without them, the final boss will send you to hell out of a ton of Japanese characters. But having rummaged in assignments of bits, I found that the game saves:
The password consists of 8 positions, each position consists of 2 bits, a total of 8 * 2 = 16 bits.
Now let's see what the raw password consists of:
(C, C) (A, L) (L, L) (L, L) (C, C) (G, G) (A, A) (G, G)
C = (sum of all positions except 1 and 5) in binary number system. The two high-order bits of the checksum are written in position 5, and the two low-order bits in position 1.
A - the number of armor (0-4) in the binary number system.
L - level number (0-20) in binary number system.
G - weapon number (0-15) in binary number system.
For coding use 4 degrees of eating a banana, which we denote by numbers:
 = 0
= 0 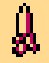 = 1
= 1  = 2
= 2  = 3
= 3
So we went to the finish line.

What would you like to say? Well, I hope this article is useful to someone. Good luck, thanks for reading.

First Road Rash
Theory
The password consists of 20 positions, each position consists of 5 bits, a total of 20 * 5 = 100 bits. These bits save game data parameters:
- the number of the occupied place (0-15) on five different tracks (0 means that you have not traveled on this route yet).
- points count (0-10485750)
- the amount of money ((-83886070) -83886070)
- current level (1-5)
- motorcycle (1-8)
Now let's see what the raw password consists of:
(U, SN, SN, SN, SN) (U, PC, PC, PC, PC) (U, RF, RF, RF, RF) (U, PD, PD, PD, PD) (U, GV, GV , GV, GV) (H, H, H, H, H) (H, H, H, H, H) (H, H, H, H, H) (H, H, H, H, H) ( N, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (U, U, L, L, L) (U, U, B, B, B) (C2, C2, C2, C2, C2) (C3 , C3, C3, C3, C3) (C4, C4, C4, C4, C4)
')
Legend
U - unused bits.
SN is the number of the occupied space in Sierra Nevada (0-15) in binary number system.
PC is the number of the occupied space in the Pacific Coast (0-15) in binary number system.
RF is the number of the occupied space in Redwood Forest (0-15) in binary number system.
PD is the number of the occupied place in Palm Desert (0-15) in binary number system.
GV is the number of the occupied place in Grass Valey (0-15) in binary number system.
H - the number of points (0-10485750) in increments = 10. The number of points is divided by 10 and the resulting number is transferred to the binary number system.
N is a bit of negative values.
M - the amount of money ((-83886070) -83886070) with a step = 10.
In order to create a positive amount of money, you need to divide the amount of money by 10 and convert the resulting number into binary number system.
In order to create a negative amount of money, you need:
- Activate a bit of negative values.
- From the number 83886080 subtract the amount of money (by module), divide the resulting balance by 10 and convert the number to the binary number system.
L is the level number (1-5) in binary number system.
B is the number of the motorcycle (0-7) in binary number system.
| Motorcycles | room |
| SHURIKEN 400 | 0 |
| PANDA 600 | one |
| BANZAI 750 | 2 |
| KAMIKAZE 750 | 3 |
| SHURIKEN 1000 | four |
| FERRUCI 850 | five |
| PANDA 750 | 6 |
| DIABLO 1000 | 7 |
C1 = (sum of positions from 1 to 17) mod64 (The resulting number is transferred to the binary number system and mirrored).
C2 = (sum of positions from 6 to 10) mod32.
C3 = (sum of positions 11 through 15) mod32.
C4 = C2 XOR C3.
Coding
Characters in the positions can take the values 0-9 and AV. The bits in the positions are encoded in accordance with the fact that 0 = 00000, 1 = 00001, 2 = 00010 ... U = 11110, V = 11111. That is, this is a simple 5 bit encoding.
An example of generating a password with a positive amount of money
Create a password that saves these parameters:
5 = 0101
3 = 0011
7 = 0111
9 = 1001
1 = 0001
10341950 points / 10 = 1034195 = 11111100011111010011
23915840 money / 10 = 2391584 = 1001000111111000100000
level 5 = 101
motorcycle number 6 = 110
(00101) (00011) (00111) (01001) (00001) (11111) (10001) (11110) (10011) (0010 *) (0100 *) (0111 *) (1110 *) (0010 *) (0000 * ) (00101) (00110) (*****) (*****) (*****)
Now we translate the values into the binary number system (* = 0):
(5) (3) (7) (9) (1) (31) (17) (30) (19) (4) (8) (14) (28) (4) (0) (5) (6 ) (0) (0) (0).
Now we calculate the first checksum:
C1 = (5 + 3 + 7 + 9 + 1 + 31 + 17 + 30 + 19 + 4 + 8 + 14 + 28 + 4 + 0 + 5 + 6) mod64 = 191mod64 = 63 = 111111 (now mirror the checksum ) = 111111 (write the resulting number instead of *).
(00101) (00011) (00111) (01001) (00001) (11111) (10001) (11110) (10011) (00101) (01001) (01111) (11101) (00101) (00001) (00101) (00110 ) (*****) (*****) (*****)
Now we calculate the second, third and fourth checksums (we must not forget that because of C1, the values of some positions have changed):
C2 = (31 + 17 + 30 + 19 + 5) mod32 = 102 mod32 = 6 = 00110.
C3 = (9 + 15 + 29 + 5 + 1) mod32 = 59mod32 = 27 = 11011.
C4 =
00110
XOR
11011
=
11101 = 29
Write the resulting password in decimal notation:
(5) (3) (7) (9) (1) (31) (17) (30) (19) (5) (9) (15) (29) (5) (1) (5) (6 ) (6) (27) (29)
Now we encode the resulting values:
5,3,7,9,1 V, H, U, J, 5
9, F, T, 5.1 5.6.6, R, T
- SN = 5 place, PC = 3 place, RF = 7 place, PD = 9 place, GV = 1 place
- points count (10341950)
- amount of money (23915840)
- current level (5)
- motorcycle (6)
- all unused bits are zero
We translate the values into the binary number system:
5 = 0101
3 = 0011
7 = 0111
9 = 1001
1 = 0001
10341950 points / 10 = 1034195 = 11111100011111010011
23915840 money / 10 = 2391584 = 1001000111111000100000
level 5 = 101
motorcycle number 6 = 110
Write the raw password and calculate 4 checksums:
(00101) (00011) (00111) (01001) (00001) (11111) (10001) (11110) (10011) (0010 *) (0100 *) (0111 *) (1110 *) (0010 *) (0000 * ) (00101) (00110) (*****) (*****) (*****)
Now we translate the values into the binary number system (* = 0):
(5) (3) (7) (9) (1) (31) (17) (30) (19) (4) (8) (14) (28) (4) (0) (5) (6 ) (0) (0) (0).
Now we calculate the first checksum:
C1 = (5 + 3 + 7 + 9 + 1 + 31 + 17 + 30 + 19 + 4 + 8 + 14 + 28 + 4 + 0 + 5 + 6) mod64 = 191mod64 = 63 = 111111 (now mirror the checksum ) = 111111 (write the resulting number instead of *).
(00101) (00011) (00111) (01001) (00001) (11111) (10001) (11110) (10011) (00101) (01001) (01111) (11101) (00101) (00001) (00101) (00110 ) (*****) (*****) (*****)
Now we calculate the second, third and fourth checksums (we must not forget that because of C1, the values of some positions have changed):
C2 = (31 + 17 + 30 + 19 + 5) mod32 = 102 mod32 = 6 = 00110.
C3 = (9 + 15 + 29 + 5 + 1) mod32 = 59mod32 = 27 = 11011.
C4 =
00110
XOR
11011
=
11101 = 29
Write the resulting password in decimal notation:
(5) (3) (7) (9) (1) (31) (17) (30) (19) (5) (9) (15) (29) (5) (1) (5) (6 ) (6) (27) (29)
Now we encode the resulting values:
5,3,7,9,1 V, H, U, J, 5
9, F, T, 5.1 5.6.6, R, T
An example of generating a password with a negative amount of money
Create a password that saves these parameters:
2 = 0010
5 = 0101
8 = 1000
11 = 1011
13 = 1101
5931870 points / 10 = 593187 = 10010000110100100011
83886080 - [- 53724780] = 30161300. 30161300/10 = 3016130 = 1011100000010111000010
level 2 = 010
motorcycle number 3 = 011
(10010) (10101) (11000) (11011) (11101) (10010) (00011) (01001) (00011) (1010 *) (1110 *) (0000 *) (0101 *) (1100 *) (0010 * ) (11010) (11011) (*****) (*****) (*****)
Now we translate the values into the binary number system (* = 0):
(18) (21) (24) (27) (29) (18) (3) (9) (3) (20) (28) (0) (10) (24) (4) (26) (27 ) (0) (0) (0)
Now we calculate the first checksum:
C1 = (18 + 21 + 24 + 27 + 29 + 18 + 3 + 9 + 3 + 20 + 28 + 0 + 10 + 24 + 4 + 26 + 7) mod64 = 291mod64 = 35 = 100011 (now mirror the checksum ) = 110001 (write the resulting number instead of *).
(10010) (10101) (11000) (11011) (11101) (10010) (00011) (01001) (00011) (10101) (11101) (00000) (01010) (11000) (00101) (11010) (11011 ) (*****) (*****) (*****)
Now we calculate the second, third and fourth checksums (we must not forget that because of C1, the values of some positions have changed):
C2 = (18 + 3 + 9 + 3 + 21) mod32 = 54mod32 = 22 = 10110
C3 = (29 + 0 + 10 + 24 + 5) mod32 = 68mod32 = 4 = 00100
C4 =
10110
XOR
00100
=
10010 = 18
Write the resulting password in decimal notation:
(18) (21) (24) (27) (29) (18) (3) (9) (3) (21) (29) (0) (10) (24) (5) (26) (27 ) (22) (4) (18)
Now we encode the resulting values:
I, L, O, R, TI, 3,9,3, L
T, 0, A, O, 5 Q, R, M, 4, I
- SN = 2 place, PC = 5 place, RF = 8 place, PD = 11 place, GV = 13 place
- points count (5931870)
- amount of money (-53724780)
- current level (2)
- motorcycle (3)
- all unused bits are one
We translate the values into the binary number system:
2 = 0010
5 = 0101
8 = 1000
11 = 1011
13 = 1101
5931870 points / 10 = 593187 = 10010000110100100011
83886080 - [- 53724780] = 30161300. 30161300/10 = 3016130 = 1011100000010111000010
level 2 = 010
motorcycle number 3 = 011
Write the raw password and calculate 4 checksums:
(10010) (10101) (11000) (11011) (11101) (10010) (00011) (01001) (00011) (1010 *) (1110 *) (0000 *) (0101 *) (1100 *) (0010 * ) (11010) (11011) (*****) (*****) (*****)
Now we translate the values into the binary number system (* = 0):
(18) (21) (24) (27) (29) (18) (3) (9) (3) (20) (28) (0) (10) (24) (4) (26) (27 ) (0) (0) (0)
Now we calculate the first checksum:
C1 = (18 + 21 + 24 + 27 + 29 + 18 + 3 + 9 + 3 + 20 + 28 + 0 + 10 + 24 + 4 + 26 + 7) mod64 = 291mod64 = 35 = 100011 (now mirror the checksum ) = 110001 (write the resulting number instead of *).
(10010) (10101) (11000) (11011) (11101) (10010) (00011) (01001) (00011) (10101) (11101) (00000) (01010) (11000) (00101) (11010) (11011 ) (*****) (*****) (*****)
Now we calculate the second, third and fourth checksums (we must not forget that because of C1, the values of some positions have changed):
C2 = (18 + 3 + 9 + 3 + 21) mod32 = 54mod32 = 22 = 10110
C3 = (29 + 0 + 10 + 24 + 5) mod32 = 68mod32 = 4 = 00100
C4 =
10110
XOR
00100
=
10010 = 18
Write the resulting password in decimal notation:
(18) (21) (24) (27) (29) (18) (3) (9) (3) (21) (29) (0) (10) (24) (5) (26) (27 ) (22) (4) (18)
Now we encode the resulting values:
I, L, O, R, TI, 3,9,3, L
T, 0, A, O, 5 Q, R, M, 4, I

Second Road Rash
Theory
The password consists of 8 positions, each position consists of 5 bits, a total of 8 * 5 = 40 bits. These bits save game data parameters:
- trails at this level (0-5)
- amount of money (0-327670)
- current level (1-5)
- motorcycle (1-16)
Now let's see what the raw password consists of:
(?, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (U, U, L , L, L) (B, B, B, B, C1) (T, T, T, T, T) (C2, C2, C2, C2, C2)
Legend
? - always equal to zero.
U - unused bits.
M - the amount of money (0-327670) with a step = 10. The amount of money is divided by 10 and the resulting number is transferred to the binary number system.
L is the level number (1-5) in binary number system.
B is the number of the motorcycle (0-15) in binary number system.
| Motorcycles | room |
| SHURIKEN 400 | 0 |
| PANDA 500 | one |
| SHURIKEN TT250 | 2 |
| PANDA 900 | 3 |
| BANZAI 7.11 | four |
| BANZAI 600 N | five |
| BANZAI 750 N | 6 |
| SHURIKEN 1000 N | 7 |
| BANZAI 7.11 N | eight |
| DIABLO 1000 N | 9 |
| PANDA 600 | ten |
| BANZAI 600 | eleven |
| BANZAI 750 | 12 |
| SHURIKEN 1000 | 13 |
| DIABLO 1000 | 14 |
| WILD THING | 15 |
T - traces passed (0-5).
The order of bits from high to low:
4 - is responsible for passing the fifth route.
3 - is responsible for the passage of the fourth route.
2 - is responsible for passing the third route.
1 - is responsible for the passage of the second route.
0 - is responsible for passing the first track.
C1 = (sum of positions from 1 to 6, not counting the 5 position) mod32 (The resulting number is transferred to the binary number system and mirrored).
C2 = ((sum of positions from 1 to 6) mod32) XOR 7 position.
Coding
Coding of values is the same as in the first part.
Password generation example
Create a password that saves these parameters:
distance trails = 10101
level number 3 = 011
motorcycle number 9 = 1001
193750 money / 10 = 19375 = 100101110101111
(0100 *) (1011 *) (1010 *) (1111 *) (00011) (1001 *) (10101) (*****)
Now we translate the values into the binary number system (* = 0):
(8) (22) (20) (30) (3) (18) (21) (0)
Now we calculate the first checksum:
C1 = (8 + 22 + 20 + 30 + 18) mod32 = 98mod32 = 2 = 00010 (now mirror the checksum) = 01000 (write the resulting number instead of *).
(01000) (10111) (10100) (11110) (00011) (10010) (10101) (*****).
Now we calculate the second checksum (you need not to forget that due to C1, the values of some positions have changed):
C2 = (8 + 23 + 20 + 30 + 3 + 18) mod32 = 102mod32 = 6mod32 = 00110.
00110
XOR
10101
=
10011 = 19
Write the resulting password in decimal notation:
(8) (23) (20) (30) (3) (18) (21) (19)
Now we encode the resulting values:
8, N, K, U 3, I, L, J
- passed the fifth, third and first tracks
- amount of money (193750)
- current level (3)
- motorcycle (9)
- all unused bits are zero
We translate the values into the binary number system:
distance trails = 10101
level number 3 = 011
motorcycle number 9 = 1001
193750 money / 10 = 19375 = 100101110101111
Write the raw password and calculate 2 checksums:
(0100 *) (1011 *) (1010 *) (1111 *) (00011) (1001 *) (10101) (*****)
Now we translate the values into the binary number system (* = 0):
(8) (22) (20) (30) (3) (18) (21) (0)
Now we calculate the first checksum:
C1 = (8 + 22 + 20 + 30 + 18) mod32 = 98mod32 = 2 = 00010 (now mirror the checksum) = 01000 (write the resulting number instead of *).
(01000) (10111) (10100) (11110) (00011) (10010) (10101) (*****).
Now we calculate the second checksum (you need not to forget that due to C1, the values of some positions have changed):
C2 = (8 + 23 + 20 + 30 + 3 + 18) mod32 = 102mod32 = 6mod32 = 00110.
00110
XOR
10101
=
10011 = 19
Write the resulting password in decimal notation:
(8) (23) (20) (30) (3) (18) (21) (19)
Now we encode the resulting values:
8, N, K, U 3, I, L, J
But that is not all!
I cooked something else ...
For dessert - Banana Prince
Let's digress a bit from the Sega console and move on to Nes (Dandy). This game is very patted my nerves. Who played, he remembers the long questions in Japanese, because of which the passing game turns into hell. Passwords in it are simple, but with a tackle. To complete the game 100% needed to collect 4 armor. But there is one problem, to get them, you had to answer a ton of questions. No matter how much I rummaged on the Internet and in my book of codes, I never found the passwords that save the collected armor. And without them, the final boss will send you to hell out of a ton of Japanese characters. But having rummaged in assignments of bits, I found that the game saves:
- the current level number (0-20) in decimal notation
- weapon number (0-15)
- armor (0-4)
The password consists of 8 positions, each position consists of 2 bits, a total of 8 * 2 = 16 bits.
Now let's see what the raw password consists of:
(C, C) (A, L) (L, L) (L, L) (C, C) (G, G) (A, A) (G, G)
Legend
C = (sum of all positions except 1 and 5) in binary number system. The two high-order bits of the checksum are written in position 5, and the two low-order bits in position 1.
A - the number of armor (0-4) in the binary number system.
L - level number (0-20) in binary number system.
| Levels | room |
| 1-1 | 0 |
| 1-2 | one |
| 1-3 | 2 |
| 2-1 | 3 |
| 2-2 | four |
| 2-3 | five |
| 3-1 | 6 |
| 3-2 | 7 |
| 3-3 | eight |
| 4-1 | 9 |
| 4-2 | ten |
| 4-3 | eleven |
| 5-1 | 12 |
| 5-2 | 13 |
| 5-3 | 14 |
| 6-1 | 15 |
| 6-2 | sixteen |
| 6-3 | 17 |
| 7-1 | 18 |
| 7-2 | nineteen |
| 7-3 | 20 |
G - weapon number (0-15) in binary number system.
Coding
For coding use 4 degrees of eating a banana, which we denote by numbers:
 = 0
= 0 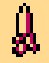 = 1
= 1  = 2
= 2  = 3
= 3Password generation example
Create a password that saves these parameters:
4 = 100
20 = 10100
15 = 1111
(**) (11) (01) (00) (**) (11) (00) (11)
Now we translate the values into the binary number system (* = 0):
(0) (3) (1) (0) (0) (3) (0) (3)
Calculate the checksum:
C = (3 + 1 + 0 + 3 + 0 + 3) = 10 = 1010. 10 (two high-order bits) 10 (two low-order bits).
Write the resulting password in decimal notation:
(2) (3) (1) (0) (2) (3) (0) (3)
It remains to convert the numbers to a banana equivalent.
- character has 4 armor
- level number (20)
- weapon number (15)
We translate the values into the binary number system:
4 = 100
20 = 10100
15 = 1111
Write the raw password:
(**) (11) (01) (00) (**) (11) (00) (11)
Now we translate the values into the binary number system (* = 0):
(0) (3) (1) (0) (0) (3) (0) (3)
Calculate the checksum:
C = (3 + 1 + 0 + 3 + 0 + 3) = 10 = 1010. 10 (two high-order bits) 10 (two low-order bits).
Write the resulting password in decimal notation:
(2) (3) (1) (0) (2) (3) (0) (3)
It remains to convert the numbers to a banana equivalent.
Conclusion
So we went to the finish line.

What would you like to say? Well, I hope this article is useful to someone. Good luck, thanks for reading.
Source: https://habr.com/ru/post/303338/
All Articles