This is all because someone has too small an exhibitor: a Hastad attack on RSA in the NeoQUEST-2016 task
 We continue to sort out the tasks of the online stage NeoQUEST-2016 and are preparing for the “ confrontation ”, where we invite everyone! You are waiting for interesting reports, demonstrations of attacks, contests, prizes and much more!
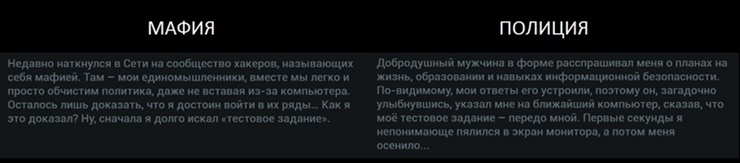
We continue to sort out the tasks of the online stage NeoQUEST-2016 and are preparing for the “ confrontation ”, where we invite everyone! You are waiting for interesting reports, demonstrations of attacks, contests, prizes and much more!Rare hack quest does without cryptography, well, NeoQUEST-2016 is no exception! In the task of the online stage, our choice fell on the RSA cryptosystem, the security of which can be talked about for a long time. For educational and cognitive purposes, we took not the most popular attack on the RSA - the Hasstad attack.
In addition, we rather confused the participants without giving them (at first glance!) Any initial data for the task. About where it was necessary to look for what to do with what was found and how to realize the Hasstad attack - we read under the cut!
Where is the task?
... this question was addressed to support@neoquest.ru by our participants. They could be understood: the texts of both legends did not really say anything.
')
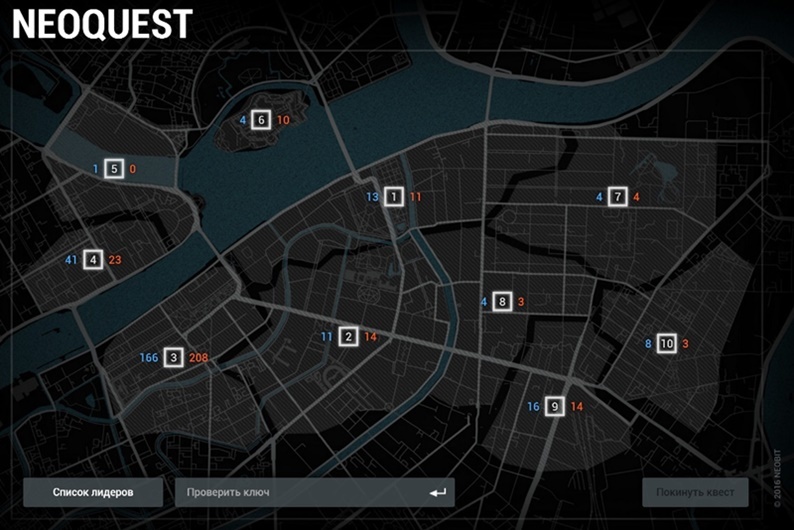
After transparent hints, the participants recalled the map on the main page of the site and went to study it.
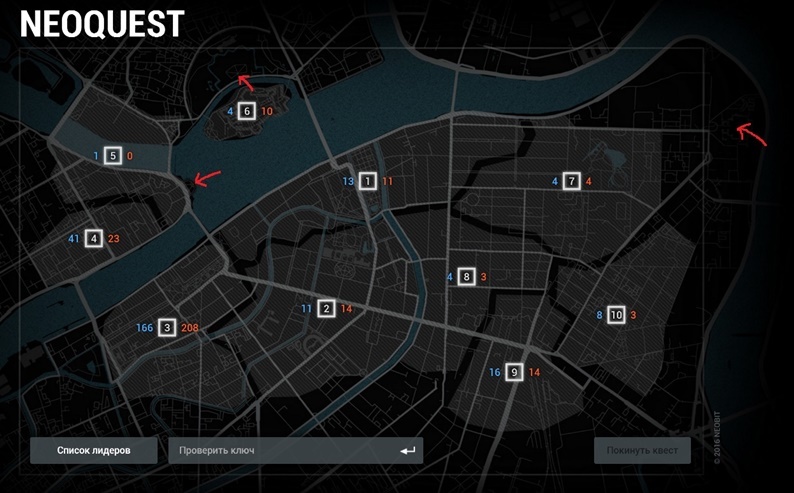
It was possible to find the source data for the task in several ways. Very attentive luckies noticed that if you move the mouse over the map, then in some points (or rather, in three!) The cursor changes to the hand, which usually appears when you hover over the link. On click, the .asn1 file was downloaded.
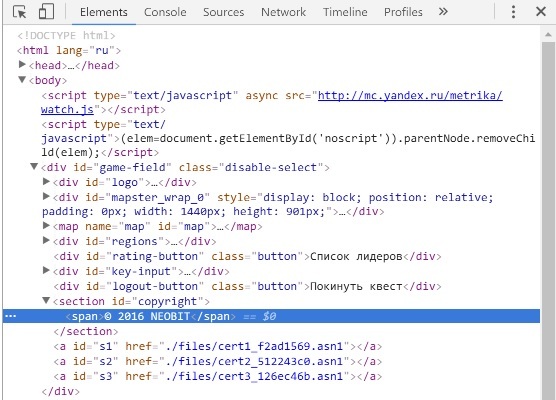
Other participants decided not to strain their eyes and looked at the site by the “inspector”, and soon somewhere under copyright they found the three hidden files: cert1_f2ad1569.asn1, cert2_512243c0.asn1, cert3_126ec46b.asn1.
Parsim ASN.1
ASN.1 is an information coding standard that is widely used, including in cryptography. You can read more about the standard in Habré (detailed, written in clear language article), and on third-party resources ( here and there ). Any data in ASN.1 is represented as a sequence "Tag - Length - Value". In this case, the “Tag” defines the data type, and the “Length” sets the size of the next “Value” field.
In order to find out what kind of information is in these three .asn1 files, they need to be parsed. There are many programs for this, for example, ASN.1 JavaScript decoder or the command-line application dumpasn1 .
Using dumpasn1, opening all three files in turn, we see the following:
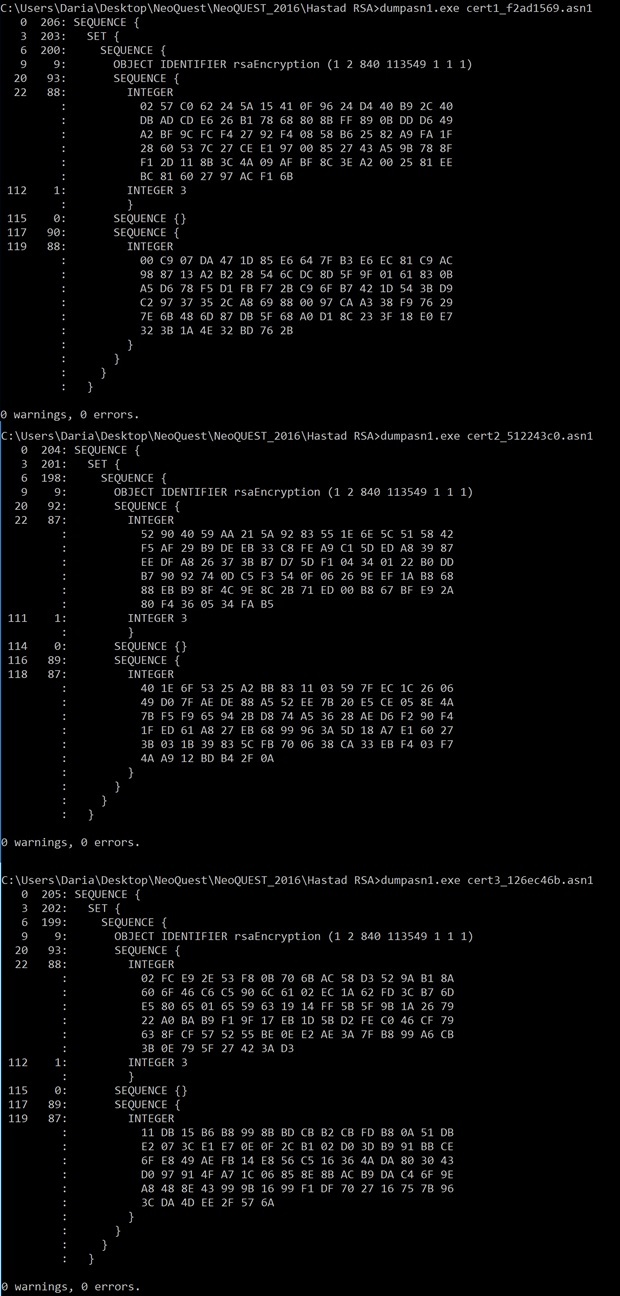
The structure of all three files is the same; the OBJECT IDENTIFIER rsaEncryption line in all three files clearly indicates RSA. Each file contains, apparently, 3 parameters of RSA, and one parameter in all three files is the same and equal to 3. We begin to study possible attacks on RSA (for example, on the wiki ), and parameter 3 is noticeably small compared to the other two parameters , suggests the idea that this is nothing more than an open exponent e! So, you can realize the attack Hastad.
We realize the attack of Hasdad
Initial data to attack
Read in detail about the attack of Hasdad here . The conditions for an attack are as follows: User A sends an encrypted message to several users. in this case, three (by the number of files): P 1 , P 2 , P 3 . Each user has his own key, represented by the “module-open exponent” pair (n i , e i ), with M <n 1 , n 2 , n 3 . For each of the three users, A encrypts the message in the corresponding public key and sends the result to the addressee.
The attacker implements the interception of messages and collects the transmitted ciphertexts (denoted as C 1 , C 2 , C 3 ), in order to restore the original message M. We carefully look at our .asn1 files: the first parameter is obviously the RSA n module, the second, as we have already found out - an open exponent, which means that the third parameter is the ciphertext. So, according to the three cipherteks you need to restore the message, which will either be the key. or give a hint to where to find the key to the task.
Why exactly can we implement it?
As is known, the message is encrypted according to the RSA scheme as follows: C = M e mod n. In the case of an open exponent equal to 3, obtaining ciphertexts looks like this:
C 1 = M 3 mod n 1
C 2 = M 3 mod n 2
C 3 = M 3 mod n 3
Knowing that n 1 , n 2 , n 3 are mutually simple, we can apply the Chinese remainder theorem to ciphertexts.
We end up with some C ' , the cubic root of which will give us the desired message M!
C ' = M 3 mod n 1 n 2 n 13
We recall that M is less than each of the three modules n i , which means that the equality holds:
C ' = M 3
So we will find our desired message M.
Software implementation of the Hastad attack
One of our participants implemented the script in Python, its detailed writeup is here , we only give the script code from there:
import math c_flag1 = 258166178649724503599487742934802526287669691117141193813325965154020153722514921601647187648221919500612597559946901707669147251080002815987547531468665467566717005154808254718275802205355468913739057891997227 N1=770208589881542620069464504676753940863383387375206105769618980879024439269509554947844785478530186900134626128158103023729084548188699148790609927825292033592633940440572111772824335381678715673885064259498347 c_flag2 = 82342298625679176036356883676775402119977430710726682485896193234656155980362739001985197966750770180888029807855818454089816725548543443170829318551678199285146042967925331334056196451472012024481821115035402 N2=106029085775257663206752546375038215862082305275547745288123714455124823687650121623933685907396184977471397594827179834728616028018749658416501123200018793097004318016219287128691152925005220998650615458757301 c_flag3 = 22930648200320670438709812150490964905599922007583385162042233495430878700029124482085825428033535726942144974904739350649202042807155611342972937745074828452371571955451553963306102347454278380033279926425450 N3=982308372262755389818559610780064346354778261071556063666893379698883592369924570665565343844555904810263378627630061263713965527697379617881447335759744375543004650980257156437858044538492769168139674955430611 def chinese_remainder(n, a): sum = 0 prod = reduce(lambda a, b: a*b, n) for n_i, a_i in zip(n, a): p = prod / n_i sum += a_i * mul_inv(p, n_i) * p return sum % prod def mul_inv(a, b): b0 = b x0, x1 = 0, 1 if b == 1: return 1 while a > 1: q = a / b a, b = b, a%b x0, x1 = x1 - q * x0, x0 if x1 < 0: x1 += b0 return x1 def find_invpow(x,n): """Finds the integer component of the n'th root of x, an integer such that y ** n <= x < (y + 1) ** n. """ high = 1 while high ** n < x: high *= 2 low = high/2 while low < high: mid = (low + high) // 2 if low < mid and mid**n < x: low = mid elif high > mid and mid**n > x: high = mid else: return mid return mid + 1 flag_cubed = chinese_remainder( [N1, N2, N3], [c_flag1, c_flag2, c_flag3] ) flag=find_invpow(flag_cubed,3) print hex(flag)[ 2 : -1 ].decode("hex") As can be seen from the code, first the parameters n i and C i were obtained from the files, which were transformed from HEX-format into whole large numbers. Then the Chinese theorem on residuals was implemented and, finally, the cube root was extracted to obtain the desired message.
key = bff149a0b87f5b0e00d9dd364e9ddaa0
The received message contains the key, the task is completed!
Finally
In continuation of the NeoQUEST assignments of past years, where participants were required to find an error in the implementation of the RSA scheme or to carry out a module decomposition attack (parse the task here ), implement Wiener 's attack, a Hustad attack was chosen that was not based on factoring.
As the statistics of the appeal of the participants of the online stage NeoQUEST-2016 in support showed, the main problem for them was the incomprehensible formulation of the task and the hidden source data. However, the file format also baffled some of the participants.
The best participants of the online stage will meet very soon at the "confrontation" on July 7 in St. Petersburg! And we invite everyone - specialists of IB firms, hackers and geeks, applicants and students of IT-specialties - to have a great time listening to reports and participating in contests, while the participating guys are having tasks! Admission is free, you only need to register on the site . NeoQUEST is another reason to visit Peter this summer!
Source: https://habr.com/ru/post/303264/
All Articles