Recently, on Geektimes I published an article where I cited some superficial statistics from the “Song of Ice and Flame” series of books. But I did not go into the most interesting part, in the graph of social relations, because the topic deserves special attention. In this article, I will demonstrate how graph theory can help in analyzing such data and present the implementation of the algorithms that I used.



Anyone interested, welcome under cat.



From the survey of the aforementioned article, I concluded that more than a third of the Geektimes audience was familiar with the book of fantasy novel, and more than half with the plot of the series. I hope the audience Geektimes and Habrahabr intersect and you may be interested in not only the algorithms used, but also the results.

')

Data

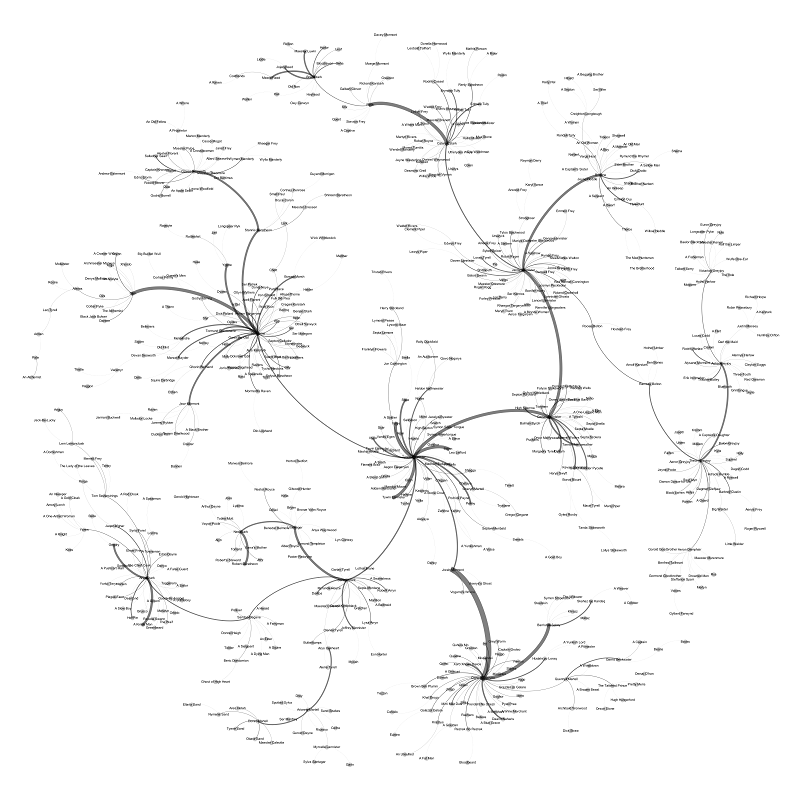
Let's start, of course, with the main thing - the data. We have a social activity graph:







It depicts characters from the world of thrones at the vertices of the graph, where the size of the vertex depends on the words spoken, and the dialogues of the characters on the edges of the graph, where the thickness of the edge depends on the number of conversations held.



General information about the graph:



The graph is undirected.

Summits (read characters): 1105

Reber (read dialogs): 3505



It's all good, but who made the list of all the conversations, and even determined their identity, you ask me (in 5 books, there are almost 2 million words ). The method of conditional random fields , I answer. Yes, machine learning was attracted to collect data and, as the model “trainer” states, the accuracy of determining the ownership of a conversation is about 75% . I will add a questionnaire at the end of the article to find out whether it is worth translating this article about how the method of conditional random fields was applied.



So, the input data format for all algorithms will be the same:



The first line contains V and E , the number of vertices and edges in the graph, respectively.



Next come the V lines with the character ID and name. After this, E lines of the form uvw are the description of edges. It means that between u and v there is an edge with weight w , where u and v is the character ID . Let me remind you that the weight means the number of dialogues between the respective characters. The weight of the vertices themselves will not be taken into account anywhere. I did not find a worthy application for him. Oh yeah, the code of the algorithms will be presented in C ++.



We, of course, need to read the data. For this, I created the definitions.h and definitions.cpp files. Further I will connect definitions.h everywhere that the code was less and the code was read easier. Each subsequent algorithm is implemented as a separate function and is called in the function main .

Degree of vertex

To begin with, we will try to implement something very simple, which is even embarrassing to call an algorithm, but it will be interesting for the reader / viewer. Find the degree of each vertex. The degree of a vertex is the number of edges incident to (adjacent to) a vertex. This parameter in the context of the graph, which we have, will show us how many “friends” the character has.



This can be done in a single pass and the complexity of this algorithm is O (V + E). If we apply and sort the result, as I did, then the complexity will be O (E + V * log (V)).





Top 10 multiply characters:

1. Tyrion Lannister: 168
   
   
2. John Snow: 128
   
   
3. Arya Stark: 104
   
   
4. Jamie Lannister: 102
   
   
5. Cersei Lannister: 86
   
   
6. Catelyn Stark: 85
   
   
7. Theon Greyjoy: 76
   
   
8. Daineris Targaryen: 73
   
   
9. Brienne: 71
   
   
10. Sansa Stark: 69
    
    

The whole list



It is interesting that in the top there was no one who is familiar with many and is obliged to maintain contact with people, Varis (he is in 25th place). But the seemingly secondary character of Brienne, on whose behalf the chapter is not yet, is in ninth place.

Bypassing the graph

So, we now turn to simple algorithms, namely, to search in depth ( Depth-first search ) and search in width ( Breadth-first search ). Both algorithms are very similar, differ only in the way around the graph. They are used when you want to go through the edges from a given vertex in the graph to another. In the case of a depth search, the graph is traversed starting from the vertex and alternately at the maximum depth along one of the outgoing edges. In the case of a search in width, the graph first goes through all its neighboring vertices, further along the neighbors of neighboring vertices, and so there are no pending vertices left. Both algorithms have O (V + E) complexity.

Graph connectivity

Find the connected components of our graph. A connected component is a subgraph in which all vertices have a path to any other vertex of the component. To do this, run the search algorithm in depth by one of the vertices, and after completion, in the next, not marked by the algorithm, vertex. Thus, each start of the search will mean a new component of connectivity.





It would be extremely strange if the graph were not connected and there was more than one component in it, wouldn’t it? But to my surprise, there were already 3 components in the graph! But looking at them, I saw that one large component was present, and 2 others, in which there was one character each (It was a smiling old man ( A smiley old man ) who talked with Arya near God's eye ( God's eye ). And the cook ( A Cook ), who played with Tirion on the ship). Nothing unusual, they have no names and it is surprising that the participants in the conversation were generally defined correctly. I, of course, added the missing edges and as a result the whole graph turned out to be connected.

Handshake Theory

The next thing we will find using the search algorithm is already wide - the maximum number of handshakes in the graph, in other words, the diameter of the graph, that is, the longest of the shortest paths between all the vertices of the graph. As it turned out, the maximum number of handshakes is 8. A good result for a work about “medieval centuries”, if we take into account the Theory of 6 handshakes . For example, one of these communication chains:



Mother Mole - Thistle - Varamyr - Jon Snow - Ned Stark - Barristan Selmy - Quentyn Martell - The Torn Prince Tattered Prince ) - Lewis Lanster ( Lewis Lanster )



This algorithm works for O (V * V + V * E). Since you need to run the BFS algorithm from each vertex of the graph. If this graph were a tree , it would take only 2 times to run BFS. First, from any vertex of the graph, and then from the most distant vertex from it. And the greatest depth of the last launch would be the diameter of the graph.



And since I found the longest paths for all the vertices of the graph, then we can calculate the average value, as well as make up the distribution of maximum paths. The average value for the length of the maximum paths turned out to be 6.16 (on average, it fits perfectly into the theory of 6 handshakes), and the total average distance is 3.6, for comparison, this parameter is 4.57 for Facebook.



The distribution of the lengths of the maximum paths:







If you look at the distribution, we see that 77 characters are “in the center” of the graph, in other words, they can contact any other character in no more than 4 others. Among them are all the main characters of the story, except for Dayneris Targaryen and Sansa Stark, and among those to whom less than five chapters in the books are on the list are Barristan Selmi, John Connington and Melisander.



Whole result

Clicks in the graph

The Bron-Kerbosh algorithm allows you to find the maximum clicks in the graph, in other words, subsets of vertices, any two of which are connected by an edge. In the context of the graph under consideration, this will make it possible to find strongly related companies that have communicated with each other in history. The complexity of the algorithm is linear with respect to the number of clicks in the graph, but in the worst case, it is exponential O (3 ^{V / 3} ), the algorithm solves the NP complete problem all the same. The algorithm itself is a recursive function, which for each vertex finds the maximum click, i.e. one in which no other vertices can be added. So, the results:



Click size distribution:







As you can see, the maximum click size is 9 characters. For example, one of these is the Lannister company: Tyrion, Jamie, Cersei, Varis, Tywin, Kevan, Pyzel, Petir and Mace Tyrell. Interestingly, all clicks of size 8 and 9 are formed in or near Royal Harbor. And the maximum click with daneris size 5.



Whole result

Spanning tree

And now let's simplify our link graph a bit, leaving only the “core” in it, the so-called spanning tree , i.e. the most important edges of connection and at the same time turning the graph into a tree with all the original vertices The Kruskal algorithm will help us in this. The algorithm is greedy, for its implementation it is only necessary to sort all edges by their weight and add each edge in turn if it connects two components. If you use the correct data structure (usually use a system of disjoint sets ), then the complexity of the algorithm is O (E (logE) + V + E) = O (E (logV)). Below is the result of the graph that has undergone these manipulations. I also removed the edges with a weight of 1 for readability.





the picture is clickable



So, from this graph you can see the main characters and their relationship with each other. As I expected, Tyrion Lannister is in the "center" of all ties, with 4 large branches emanating from him: Cersei Lannister, John Snow, Sansa Stark and Jorah Mormont (Daineris branch). The last, in turn, heroes of the next level of connections. Quite an expected result, isn't it?



Whole result





But how many spanning trees, including not only the maximum can be built? Incredibly much in this column, of course. But they can be calculated using the Kirchhoff theorem . The theorem says that if we construct a matrix where all elements of the adjacency matrix are replaced with opposite ones, and the degrees of the corresponding vertices are on the main diagonal, then all algebraic complements of the resulting matrix will be equal and this value will be the number of spanning trees of the graph.

Bridges and Hinges

Bridges in the graph are called edges, as they are removed, the number of connected components increases. Similar definitions are for hinges, but unlike bridges, hinges are vertices, as they are removed, the number of connected components increases. In this column, the presence of bridges will mean that in the world of thrones there are connections that are the only source of communication between individual groups of characters. The hinges are heroes who are the only mediator to a group of other characters. Bridges and hinges are not very hard to look for. To do this, we need a familiar depth-depth search algorithm, but slightly modified. It is necessary to use the so-called entry time to the vertex and the exit time function ( fout ) on the vertex, which will take the values ​​of the minimum entry time and the vertex fout values ​​at which the depth search is passed, thus, when passing the edge, it turns out that the function value fout at the top is more than the time of entry into it, then it will be a bridge, as well as a hinge, and if it is equal, then only a hinge. In other words, we check if we return to the same edge / vertex after the detour and only to it in the detour of a part of the graph, if so, this will be the required bridge or hinge.



As expected, all the hinges and bridges covered only irrelevant characters. The number of vertices in the components that would be isolated, by removing the hinges and bridges, does not exceed 4x. This means that there is no hero who could not be sacrificed. All are interconnected through at least two other characters.



Whole result

Minimum cut

But it’s still interesting to know how many heroes you need to “kill” in order to completely eliminate the contact of the two most popular (according to the above statistics) characters, such as Tirion Lannister and Arya Stark, or John Snow and Cersei Lannister. For this we will use the algorithm Dinnitsa . First, let's understand how the algorithm works.



By the Ford-Fulkerson theorem, it follows that the magnitude of the maximum flow in a graph of paths is equal to the value of the carrying capacity of its minimum cut. In other words, we can find the minimum cut between two vertices (sink and source) if we find the maximum flow between these vertices. Algorithm Dinitsa just allows you to find the value of the maximum flow and, in fact, the flow itself. I will not analyze in detail the algorithm itself and give you the opportunity to understand it yourself. To understand the result obtained, it is enough to know that the flow is a certain function that, for each edge lying in the path from the source to the drain, determines a positive value that does not exceed the capacity of this edge. For simplicity, one can imagine a pipe system with water, where the volume of water flowing from the source to the drain at time t is the flow quantity.



The task I set is slightly different from the one that the algorithm solves. The fact is that the flow is defined on the edges, and if we find the minimal cut, then it will cut the graph along the edges, i.e. connections in the graph, but we need to cut the graph not at the edges, but at the vertices, i.e. characters. To solve this problem it is necessary to subject the graph to small changes. We split each vertex in the graph, say, instead of the vertex v , we have vertices v ₁ and v ₂ , then if there was an edge between two vertices v and u , then we redirect v ₁ to u ₂ and u ₁ to v ₂ , instead of an edge (u , v) we get the edges (v ₁ , u ₂ ) and (u ₁ , v ₂ ) . And between each forked vertices v ₁ and v ₂ we draw an edge (v ₂ , v ₁ ) . In the resulting, already oriented graph, all the links will be preserved, but where there were vertices before, edges will appear. If the weight of these edges is 1, and all the others, say, infinity (in practice, you can use the number of vertices in the graph), then the edge between the split vertices will be a weak link in the graph and, according to the “fuse” principle, will not allow more flow through will give the opportunity to find out the number of vertices that need to be removed in order for the graph to become disconnected. And then we run the algorithm Dinica on the resulting graph.



The complexity of the algorithm is O (n ² m). Therefore, we will search for the value of the maximum flow not for all pairs of vertices, but only for the characters that have the greatest number of connections, otherwise for a given graph the complexity will be O (n ⁵ ), where n = 1000 and everything will work for many hours. Below I will give the results on the top 100 characters on the links.



I was a little surprised at the results. It turned out that in the top 100, you can cut the graph by getting rid of at least 6 characters. All such connections contain either John Connington or Euron Greyjoy as a drain / source. But this is not the main characters. Interestingly, in the top 10, basically the minimum flow is about 45. For example, between Tirion and Arya, the flow is 53, and between John Snow and Cersei 42. But there is also a character who can be separated by removing 16 other characters. This is Dayneris Targaryen, not surprising, because she is the most distant heroine on the map of thrones.



It would also be interesting to find out who is the most "important" hero in the streams. Those.through whom most often flows the maximum flow. There is something to be surprised. Top 10 important characters in the streams (in brackets the corresponding number of entries in the streams):

1. Tyrion Lannister (4109)
   
   
2. Jamie Lannister (3067)
   
   
3. Arya Stark (3021)
   
   
4. John Snow (2883)
   
   
5. Eddard Stark (2847)
   
   
6. Cersei Lannister (2745)
   
   
7. Theon Greyjoy (2658)
   
   
8. Brienne (2621)
   
   
9. Sandor Klegane (2579)
   
   
10. Sansa Stark (2573)
    
    

, , ( ) . , , , . , 10 , , , 10 :



11.

12.

13.

14.

15.

16.

17.

18.

19.

20.



6 5. . ?



, , «» , , , . (A Man) (A Guard). , .









. , . , , . GitHub, .

References:

GitHub



Gephi ,

— Adam Foster



, , : , ?