Probably, anyone who is interested in regular expressions and reads Habr, saw this crossword from regular expressions:

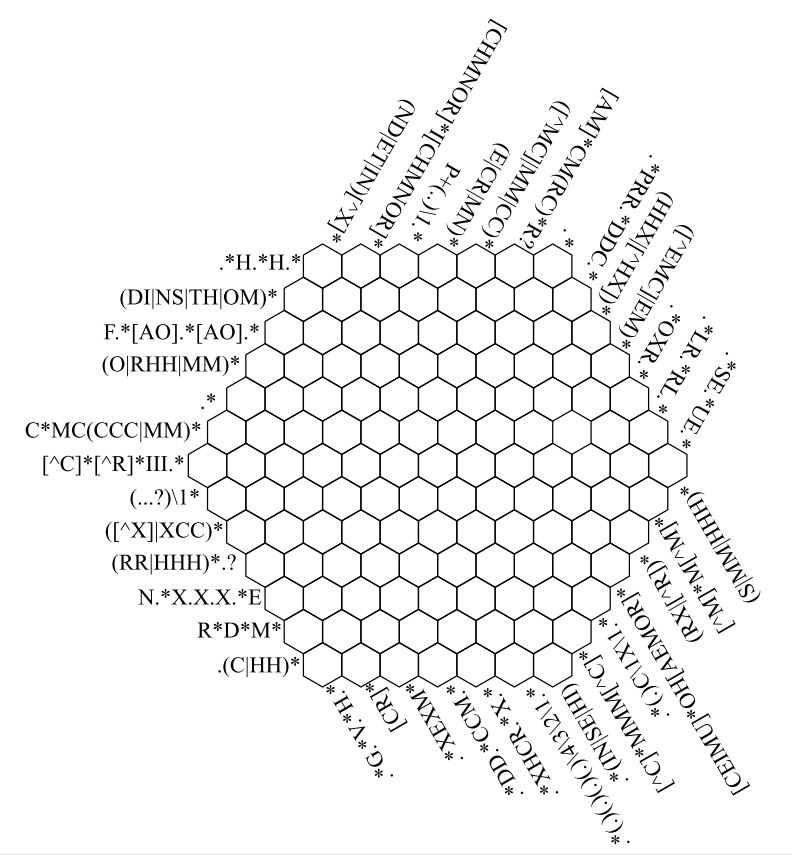
It takes from 30 minutes to several hours to solve it, but your computer can solve it in just a few minutes. And not only this crossword puzzle, but any crossword from regular expressions can be done by the algorithm under the cut.

I will try to give as little code as possible - you will find all the code written in Python3 on GitHub .

Step 0. Notation and axioms

Axiom. If a regular expression crossword has a unique finite solution, then all the characters that will be encountered in the solution are not specified by negative character classes and not by the metacharacter .

That is, suppose there are only character classes in a certain crossword: [ABC] , [^ABC] , then the solution of the crossword will consist solely of the characters A , B and C

Atom. An “atom” is a character class, a single literal, or a metacharacter of a character class that is part of the regular expression being parsed.

One "atom" - one character in the text. The concept of "atom" will be used not to confuse them with character classes inside a regular expression.

For example, the regular expression [ABC]*ABC[^ABC].\w consists of seven "atoms" [ABC], A, B, C, [^ABC], . , \w [ABC], A, B, C, [^ABC], . , \w

Crossword map, map. An array of dependencies between different regular expressions for a single crossword puzzle cell. The card contains information that in this field cell there is (for example) the 1st character of the 3rd regular expression, as well as the 5th character of the 8th regular expression, as well as the 3rd character of the 12th regular expression. Simply put - in which positions regular expressions intersect.

Step 1. Enumerate all the options for "atoms"

If you try to solve a crossword puzzle "head on" by a complete enumeration of all the characters, then immediately there will be a problem that you will not be able to wait a few million years, too many options. And yet, the algorithm is a complete search, but not individual characters, but "atoms".

For example, take a regular expression .*(IN|SE|HI) . In this crossword, it should be a string of 13 characters in length.

First we find in the regular expression all the unique "atoms" by the regular expression:

 reChars = r"\[\^?[az]+\]|[az]|\." reCharsC = re.compile( reChars, re.I ) 

It searches for character classes, single characters, and the dot metacharacter. Currently there is no support for metacharacters like \w , \d , etc., only the most necessary.

In the expression under consideration, we find such "atoms":

 [ '.', 'I', 'N', 'S', 'E', 'H' ] 

"Atoms" must be "atomized" in order to treat their string notation as an inseparable whole, rather than individual characters:

 def repl( m ): return "(?:"+re.escape( m.group(0) )+")" self.regex2 = reCharsC.sub( repl, self.regex ) 

At the input .*(IN|SE|HI) , at the output (?:\.)*((?:I)(?:N)|(?:S)(?:E)|(?:H)(?:I)) . What will it give? Now you can iterate over all "atoms" for a length of 13 "atoms", apply self.regex2 to the resulting string and check for consistency. For example:

The result of a complete iteration to the regular expression under consideration will be an array of three elements:

 [ '...........IN', '...........SE', '...........HI' ] 

Agree that a very obvious result?

You can experiment with different regular expressions like this:

 import regexCrossTool as tool print( tool.singleRegex( regex, length ).variants ) 

Step 2. Optimization

In the previous step, it was so easy to say that a regular expression .*(IN|SE|HI) will give only 3 possible variants of the string, but in fact in the expression 6 "atoms" and the length 13 "atoms", which means 6 to 13 degrees of options for enumeration.

A few days of iteration is not the most promising prospect, so the first optimization is essentially only for this expression, but in fact all the optimizations are written in an honest way - they parse the regular expression at the input and optimize the calculations if they meet a suitable template.

Expression .*(IN|SE|HI) very easy to optimize:

 reCh = r"(?:"+reChars+")+" re1 = r"(?!^)\((?:"+reCh+r"\|)+"+reCh+r"\)$" 

We look for an alternative at the end of the line, check that all parts of the alternative are the same length, select everything to the left of this alternative and process them separately, taking into account that the length of the expected result is reduced by the length of the part of the alternative.

singleRegex( ".*", 11 ) will return only one possible option ...........
In the cycle we go through all returned options and all parts of the alternative. The concatenations are returned as the result for the original regular expression.

Opening hours have been reduced from a few days to 20 minutes. Good result, but you need better.

The following optimization is very similar to the first. We optimize the regular expression, which is represented by just one alternative and quantifier to the alternative. There are several such expressions in this crossword: (DI|NS|TH|OM)* , (O|RHH|MM)* , (E|CR|MN)* , (S|MM|HHH)*

Instead of a complete search, we will write a simple recursive function:

 def recur( arr, string, length ): res = [] for i in arr: newstr = string + i lenChars = len( reCharsC.findall( newstr ) ) if lenChars == length: res.append( newstr ) elif lenChars > length: pass else: recres = recur( arr, newstr, length ) for j in recres: res.append( j ) return res recur( r"(DI|NS|TH|OM)*", "", 12 ) 

The result will be obtained in a fraction of a second, and not in a minute and a half, as before optimization.

Another optimization applies to most regular expressions.
We are looking for two or more single literals, not inside a character class [...] and if there was no bracket ( .

Brackets are avoided because it can mean anything: group, condition, recursion. Parsing regular expressions with regular expressions is not the best idea, so it’s better not to bother with complex optimizations. Let them optimize what they can and what they cannot wait.

I forgot to add that all optimizations are recursive, so several optimizations can be applied to one regular expression. Consider the expression [AO]*abc[AO]*def - it will be optimized in 2 passes.

First, replace abc with [a] , get [AO]*[a][AO]*def , replace def with [aa] on the second pass, get [AO]*[a][AO]*[aa]

As a result, instead of seven unique character classes [ '[AO]', 'a', 'b', 'c', 'd', 'e', 'f' ] there are three [ '[AO]', '[a]', '[aa]' ] - so full brute force will go much faster, but before returning the result, you need to make the inverse replacements of [a] with abc and [aa] with def .

The result of optimizations: all options for all regular expressions are considered approximately 40 seconds.

Step 3. Create a crossword map

The algorithm is in the hexaMap.py module and it makes no sense to consider it.
You give him the length of the minimum face of the hexagonal field, and in return the map of this field is returned.

 import hexaMap maps = hexaMap.getMap( 7 ) printer = hexaMap.getPrinter( 7 ) 

printer - the function that receives the result of the calculations will print the solution in accordance with the card.

Step 4. Merge

The regular expression .*(IN|SE|HI) will return three options [ '...........IN', '...........SE', '...........HI' ] , we will place them under each other, to make it clearer what is next in question:

 ...........IN ...........SE ...........HI 

Only the metacharacter can be found in the zero position . and so on up to the 10th position.
In the 11th position there can be three characters I , S , H
In the 12th position there may be three characters N , E , I

Create sets ( set() ) for each position separately - this is the union.
The union occurs for each regular expression separately and shows as a result what characters can be in certain positions in the given regular expression.

Metacharacters and character classes will also be converted to sets. Remember the axiom? Create a complete list of characters that make up the crossword puzzle solution:

 def getFullABC( self ): result = set() for i in self.cross.regexs: for j in reCharsC.findall( i ): if not re.match( r"\[\^", j ) and not j == ".": result = result.union( self.char2set( j ) ) return result self.fullABC = self.getFullABC() 

This complete list matches the metacharacter . , and negative classes are obtained by subtracting from the full list of characters in the negative class. To convert "atoms" into sets, use the function:

  def char2set( self, char ): char=char.lower() result = None def convDiap( diap ): return re.sub( r"([az])\-([az])", repl, diap, flags=re.I ) def repl( m ): # dh -> defgh res = "" for i in range( ord( m.group(1) ), ord( m.group(2) )+1 ): res+= chr( i ) return res char = char.replace( ".", "[az]" ) char = convDiap( char ) if re.fullmatch( "[az]", char, re.I ): result = set( [char] ) elif re.fullmatch( r"\[[az]+\]", char, re.I ): result = set( char.replace( "[", "" ).replace( "]", "" ) ) elif re.fullmatch( r"\[\^[az]+\]", char, re.I ): result = set( char.replace( "[", "" ).replace( "]", "" ).replace( "^", "" ) ) result = self.fullABC - result return result 

The line char = char.lower() makes a crossword puzzle case-insensitive, if you need to solve a case-sensitive crossword puzzle, you will need to remove it and all re.I flags in the code, but this is pure hardcore, not a crossword puzzle.

Step 5. Crossing

The results of the merger are reviewed in accordance with the map. For example, the 1st character of the 3rd regular expression after the merge may contain {'a', 'b', 'c', 'd'}
The 5th character of the 8th regular expression after the union can contain {'a', 'c', 'd', 'x'}
The 3rd character of the 12th regular expression after the union may contain {'c', 'f', 's'}
This means that in this cell of the crossword puzzle field there can only be the character c

Having obtained the result of the intersection, it must be placed back into the result of the union in all three dimensions. Sets {'a', 'b', 'c', 'd'} , {'a', 'c', 'd', 'x'} , {'c', 'f', 's'} replace with set {'c'} .

Step 6. Filtering options

In the previous step, we changed the intersection results.
For example, in the 1st character of the 3rd regular expression instead of {'a', 'b', 'c', 'd'} returned {'c'} , respectively, the options that were given to this position {'a', 'b', 'd'} .

If at this step at least one option was removed in any regular expression, then we return to step 4, that is, we merge again and again, intersect and filter until these actions bear fruit.

Here is what we get as a result:

  nhpehasdiomomthf * * nx * xphmm * mmm * rhhmcxnmmcrxemcmccccm mmmmm * rxrcmiiihxls * * e * r * * * * orevcxcc * h * xccrrrrhhhrruncxdx * xlerrdd * * * * gcchh * * 

Asterisks are where the sets continue to contain several values, which means praise to the creators of the crossword, they created it so competently that without analyzing the backlinks it can not be solved.

Step 7. Backlink Analysis

Backlinks are the only thing that was not properly processed in the variants, because, for example, the regular expression (...?)\1* for length 6 will return the only option ...... , that there is a backward in it The link was not used in any way.

Analysis is a big word. The game again comes full bust. After a complete search, try again steps 4-6 and so on until the result is obtained:

  nhpehasdiomomthfoxnxa xphmmommmmrhhmcxnmmcr xemcmccccmmmmmmhrxrcm iiihxlsoreoreoreorevc xcchhmxccrrrrhhhrrunc xdxexlerrddmmmmgcchhc c 

What's next?

Then you can solve crossword puzzles from any regular expressions, no matter what intricate constructions they contain, because the algorithm honestly applies this "atomized" regular expression to "atoms", which means it can contain all possible syntactic constructions of any complexity.

If there are character classes in the crossword that are not currently supported, welcome to GitHub, because to add new character classes you need to change only char2set and reChars .

If you would like to have characters like ( , [ , then again, the GitHub is open. It’s enough to build a full-fledged regular expression syntax tree and analyze it instead of regular expression parsing.

Thank you for your attention, I hope that you did not get bored from reading this small article.