Fountain codes
Today we will talk about fountain codes . They are also called "non-fixed speed codes." Fountain code allows you to take, for example, any file, and convert it into a virtually unlimited number of coded blocks. Having some subset of these blocks, you can restore the original file, provided that the size of this subset is slightly larger than the file size. In other words, this code allows you to create a "fountain" of the encoded data. The recipient can restore the original data by collecting enough “drops” from the fountain, and it doesn't matter what “drops” he has, and which ones he missed.

A remarkable property of fountain codes is that their use allows you to send data via unreliable communication channels, for example, via the Internet, without relying on knowledge of the level of packet loss, and without requiring the recipient to contact the sender to recover the missing data fragments. It is easy to see that such opportunities will be very useful in many situations. Among them, for example, sending information over broadcast communication channels, as in video transmission systems on request. The same category of tasks includes the operation of the Bittorrent protocol and other similar ones, when fragments of a file are distributed among a large number of peers.
It may seem that the fountain codes should be arranged terribly difficult. But this is not the case. There are different implementations of this algorithm, we suggest starting with the simplest of them. This is the so-called Labie transform code, commonly referred to as LT code, from Luby Transform Code . When using this variant of fountain codes, the blocks are encoded as follows:
As you can see, there is nothing complicated. But it should be noted that much in this scheme depends on the so-called distribution of powers of the code symbols, on how they choose the number of blocks to be combined. To this question we will return. From the description, you can see that some of the coded blocks are actually created using only one block of source data, while several source blocks are involved in coding most of the blocks.
Here is another coding feature, not quite obvious at first glance. It lies in the fact that as long as we allow the recipient to know exactly which blocks we combine in order to get the output block, we do not need to explicitly transmit this list. If the sender and the recipient agree on a certain pseudo-random number generator, you can initialize the generator with a randomly chosen number and use it to select the degree distribution and the set of source blocks. The initial number is simply sent along with the coded block, and the recipient can use the same procedure as the sender used to encode to restore the list of source blocks.
The decoding procedure is a bit more complicated, although it is also quite simple.
Consider the decoding example in order to better understand everything. Suppose we get five coded blocks, each one byte long. We also obtained information on the source blocks from which each of them was constructed. These data can be represented as a graph.
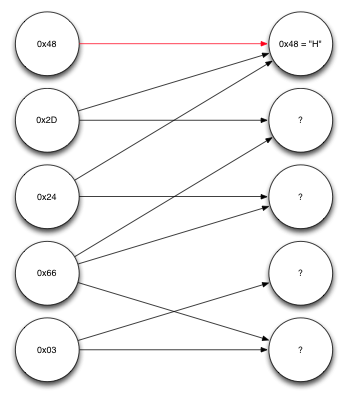
Graph representing the data
Nodes on the left are coded blocks received. The nodes on the right are source blocks. The first of the received blocks, 0x48, as it turned out, was formed with the participation of only one source block, the first one. So we already know what that block was. Moving in the opposite direction along the arrows pointing to the first source block, we see that the second and third coded blocks depend only on the first source block and on one another. And, since the first source block is already known, we can perform an XOR operation on the received blocks and the first source block and decode a few more blocks.
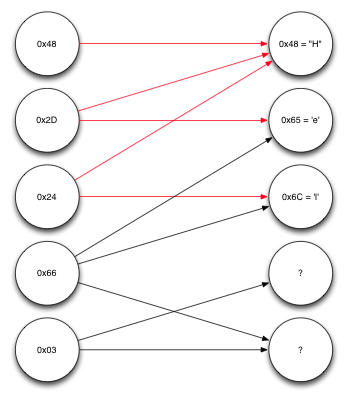
Continue decoding the message
Repeating the same procedure again, you can see that it is now known enough to decode the fourth block, which depends on the second and third source blocks, each of which is already decoded. Performing an XOR operation on them allows you to find the fifth, that is, the last source block in the list, as shown in the figure below.

Decoded fifth source block
And, finally, you can now decode the last of the remaining source blocks, which, ultimately, will give the message that the sender wanted to send to the recipient.

Fully decoded message
Admittedly, the example is artificial. Here we proceed from the assumption that only the blocks necessary for decoding the original message are received. In addition, among the blocks there is nothing superfluous, and the blocks themselves are arranged in a very convenient order. But this is just a demonstration of the principles of operation of fountain codes. We are sure that thanks to this example you will be able to understand how the same procedures work with larger blocks and longer files.
It was said earlier that how the number of source blocks is selected, of which each of the encoded blocks should consist of, or the distribution of powers of the code symbols, is very important. And, in fact, the way it is. Ideally, the algorithm should generate a small number of coded blocks, to create which only one source block is used. It is necessary for the recipient to proceed with the decoding of the message. However, the majority of coded blocks should depend on a small number of other blocks. The whole thing - in the correct selection of the distribution. A similar distribution, perfect for our purposes, exists. It is called the ideal distribution of the soliton .
Unfortunately, in practice, this distribution is not so perfect. The fact is that random variations lead to the fact that some blocks of the source are not used, or to the fact that decoding stops when the decoder ends with known blocks. One of the variants of such a distribution, called the robust soliton distribution, makes it possible to improve the performance of the algorithm, generating more blocks from a very small number of source blocks, as well as generating some blocks that are a combination of all or nearly all of the source blocks. This is done to facilitate the decoding of a certain number of the last blocks.
Here, in brief, how fountain codes work, and, in particular, LT codes. It must be said that LT codes are the least effective known fountain codes, but they are also the easiest to understand.
Before we end this conversation, here’s another thought. Fountain codes can look perfect for systems like Bittorrent, allowing sids to generate and distribute a virtually unlimited number of blocks, more or less eliminating the “last block” problem in cases where there are few of them, and ensuring that two random peers almost always have useful information which can be shared with each other. However, there is one important problem. The fact is that it is very difficult to verify the data received from peers.
Peering protocols use secure hashing functions, such as SHA1, while the trusted party, the creator of the distribution, provides a list of valid hashes to all peers. Each peer, using this data, can check loaded fragments of a file. However, when using fountain codes, this scheme of work becomes more complicated. There is no way to calculate, for example, the SHA1 hash of the encoded fragment, even knowing the hashes of the individual fragments that took part in its formation. And we cannot trust other peers to calculate this hash for us, since they can simply deceive us. We can wait until we collect the entire file, and then, using the list of invalid fragments, we can try to find the incorrect encoded fragments, but this is difficult and unreliable. Moreover, with this approach, errors can be found only in the final assembly of the file, that is, it will most likely take too much time. One possible alternative is for the distribution creator to publish the public key and sign each generated block. Thus, we can check the coded blocks, but there is a serious minus here. The fact is that only the creator of the distribution can generate the correct blocks, which means we immediately lose most of the advantages of using fountain codes. It seems that here we are at an impasse. However, there are alternatives, for example, a very clever scheme called homomorphic hashing. Although it is not perfect.
We talked about the basics of fountain codes. Varieties of this algorithm have found practical application in areas where its merits clearly outweigh the disadvantages. If you are interested in this topic and you want to go deeper into it, read this material on fountain codes. In addition, it will be useful to get acquainted with Raptor-codes , which, slightly complicating LT-codes, significantly improve their effectiveness. Thanks to their use, you can reduce the amount of transmitted data and the computational complexity of the algorithm.

A remarkable property of fountain codes is that their use allows you to send data via unreliable communication channels, for example, via the Internet, without relying on knowledge of the level of packet loss, and without requiring the recipient to contact the sender to recover the missing data fragments. It is easy to see that such opportunities will be very useful in many situations. Among them, for example, sending information over broadcast communication channels, as in video transmission systems on request. The same category of tasks includes the operation of the Bittorrent protocol and other similar ones, when fragments of a file are distributed among a large number of peers.
Basic principles
It may seem that the fountain codes should be arranged terribly difficult. But this is not the case. There are different implementations of this algorithm, we suggest starting with the simplest of them. This is the so-called Labie transform code, commonly referred to as LT code, from Luby Transform Code . When using this variant of fountain codes, the blocks are encoded as follows:
- Choose from a range of 1 - k a random number d. The range corresponds to the number of blocks in the file. Below we talk about how best to choose d.
') - Randomly select d file blocks and combine them. In our case, the operation XOR is well suited.
- The block received at the previous step is transmitted along with information on which blocks it was created from.
As you can see, there is nothing complicated. But it should be noted that much in this scheme depends on the so-called distribution of powers of the code symbols, on how they choose the number of blocks to be combined. To this question we will return. From the description, you can see that some of the coded blocks are actually created using only one block of source data, while several source blocks are involved in coding most of the blocks.
Here is another coding feature, not quite obvious at first glance. It lies in the fact that as long as we allow the recipient to know exactly which blocks we combine in order to get the output block, we do not need to explicitly transmit this list. If the sender and the recipient agree on a certain pseudo-random number generator, you can initialize the generator with a randomly chosen number and use it to select the degree distribution and the set of source blocks. The initial number is simply sent along with the coded block, and the recipient can use the same procedure as the sender used to encode to restore the list of source blocks.
The decoding procedure is a bit more complicated, although it is also quite simple.
- Restore the list of source blocks that were used to create the coded block.
- For each source block from this list, if it has already been decoded, perform an XOR operation with the encoded block and remove it from the list of source blocks.
- If at least two source blocks remain in the list, add the coded block to the temporary storage area.
- If only one source block remains in the list, it means that the next source block was successfully decoded! You need to add it to the decoded file and go through the list of temporary storage, repeating this procedure for any source blocks that contain the found block.
0x48 0x65 0x6C 0x6C 0x6F, world!
Consider the decoding example in order to better understand everything. Suppose we get five coded blocks, each one byte long. We also obtained information on the source blocks from which each of them was constructed. These data can be represented as a graph.

Graph representing the data
Nodes on the left are coded blocks received. The nodes on the right are source blocks. The first of the received blocks, 0x48, as it turned out, was formed with the participation of only one source block, the first one. So we already know what that block was. Moving in the opposite direction along the arrows pointing to the first source block, we see that the second and third coded blocks depend only on the first source block and on one another. And, since the first source block is already known, we can perform an XOR operation on the received blocks and the first source block and decode a few more blocks.

Continue decoding the message
Repeating the same procedure again, you can see that it is now known enough to decode the fourth block, which depends on the second and third source blocks, each of which is already decoded. Performing an XOR operation on them allows you to find the fifth, that is, the last source block in the list, as shown in the figure below.

Decoded fifth source block
And, finally, you can now decode the last of the remaining source blocks, which, ultimately, will give the message that the sender wanted to send to the recipient.

Fully decoded message
Admittedly, the example is artificial. Here we proceed from the assumption that only the blocks necessary for decoding the original message are received. In addition, among the blocks there is nothing superfluous, and the blocks themselves are arranged in a very convenient order. But this is just a demonstration of the principles of operation of fountain codes. We are sure that thanks to this example you will be able to understand how the same procedures work with larger blocks and longer files.
About perfect distribution
It was said earlier that how the number of source blocks is selected, of which each of the encoded blocks should consist of, or the distribution of powers of the code symbols, is very important. And, in fact, the way it is. Ideally, the algorithm should generate a small number of coded blocks, to create which only one source block is used. It is necessary for the recipient to proceed with the decoding of the message. However, the majority of coded blocks should depend on a small number of other blocks. The whole thing - in the correct selection of the distribution. A similar distribution, perfect for our purposes, exists. It is called the ideal distribution of the soliton .
Unfortunately, in practice, this distribution is not so perfect. The fact is that random variations lead to the fact that some blocks of the source are not used, or to the fact that decoding stops when the decoder ends with known blocks. One of the variants of such a distribution, called the robust soliton distribution, makes it possible to improve the performance of the algorithm, generating more blocks from a very small number of source blocks, as well as generating some blocks that are a combination of all or nearly all of the source blocks. This is done to facilitate the decoding of a certain number of the last blocks.
Here, in brief, how fountain codes work, and, in particular, LT codes. It must be said that LT codes are the least effective known fountain codes, but they are also the easiest to understand.
Peer Networks and the Problem of Trust
Before we end this conversation, here’s another thought. Fountain codes can look perfect for systems like Bittorrent, allowing sids to generate and distribute a virtually unlimited number of blocks, more or less eliminating the “last block” problem in cases where there are few of them, and ensuring that two random peers almost always have useful information which can be shared with each other. However, there is one important problem. The fact is that it is very difficult to verify the data received from peers.
Peering protocols use secure hashing functions, such as SHA1, while the trusted party, the creator of the distribution, provides a list of valid hashes to all peers. Each peer, using this data, can check loaded fragments of a file. However, when using fountain codes, this scheme of work becomes more complicated. There is no way to calculate, for example, the SHA1 hash of the encoded fragment, even knowing the hashes of the individual fragments that took part in its formation. And we cannot trust other peers to calculate this hash for us, since they can simply deceive us. We can wait until we collect the entire file, and then, using the list of invalid fragments, we can try to find the incorrect encoded fragments, but this is difficult and unreliable. Moreover, with this approach, errors can be found only in the final assembly of the file, that is, it will most likely take too much time. One possible alternative is for the distribution creator to publish the public key and sign each generated block. Thus, we can check the coded blocks, but there is a serious minus here. The fact is that only the creator of the distribution can generate the correct blocks, which means we immediately lose most of the advantages of using fountain codes. It seems that here we are at an impasse. However, there are alternatives, for example, a very clever scheme called homomorphic hashing. Although it is not perfect.
Conclusion
We talked about the basics of fountain codes. Varieties of this algorithm have found practical application in areas where its merits clearly outweigh the disadvantages. If you are interested in this topic and you want to go deeper into it, read this material on fountain codes. In addition, it will be useful to get acquainted with Raptor-codes , which, slightly complicating LT-codes, significantly improve their effectiveness. Thanks to their use, you can reduce the amount of transmitted data and the computational complexity of the algorithm.
Oh, and come to work with us? :)wunderfund.io is a young foundation that deals with high-frequency algorithmic trading . High-frequency trading is a continuous competition of the best programmers and mathematicians of the whole world. By joining us, you will become part of this fascinating fight.
We offer interesting and challenging data analysis and low latency tasks for enthusiastic researchers and programmers. Flexible schedule and no bureaucracy, decisions are quickly made and implemented.
Join our team: wunderfund.io
Source: https://habr.com/ru/post/302638/
All Articles