Developing a class for working with Markov chains
Today I would like to tell you about writing a class to simplify working with Markov chains.
I ask under the cat.
Initial knowledge:
Representation of graphs in the form of an adjacency matrix, knowledge of basic concepts about graphs. Knowledge of C ++ for the practical part.
')
In simple terms, the Markov Chain is a weighted graph. At its vertices are events, and as the weight of the edge connecting vertices A and B is the probability that event A will be followed by event B.
Quite a lot of articles have been written about the use of Markov chains, but we will continue to develop a class.
I will give an example of a Markov chain:
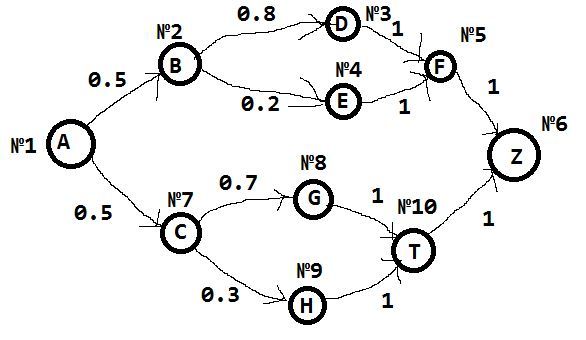
In the following, we will consider this scheme as an example.
Obviously, if there is only one outgoing edge from the vertex A, then its weight will be equal to 1.
At the vertices we have events (from A, B, C, D, E ...). On the edges there is a probability that after the i-th event there will be an event j> i. For convention and convenience, I numbered the vertices (# 1, # 2, etc.).
The matrix will be called the adjacency matrix of an oriented weighted graph, which we represent the Markov chain. (more on that later). In this particular case, this matrix is also called the matrix of transition probabilities, or simply the transition matrix.
We will represent the Markov chains using a matrix, namely, the adjacency matrix with which we represent the graphs.
I recall:
Learn more about adjacency matrices in the course of discrete mathematics.
In our case, the matrix will have a size of 10x10, we will write it:
Take a closer look at our matrix. In each row we have non-zero values in those columns whose number coincides with the subsequent event, and the non-zero value itself is the probability that this event will occur.
Thus, we have the values of the probability of an event with a number equal to the column number after the event with a number equal to the row .
Those who know probability theory could guess that each line is a probability distribution function.
1) we initialize the initial position k by the zero vertex.
2) If the vertex is not finite, then we generate the number m from 0 ... n-1 based on the probability distribution in the row k of the matrix, where n is the number of vertices and m is the number of the next event (!). Otherwise we leave
3) The number of the current position k is equal to the number of the generated vertex
4) Step 2
Note: the vertex is finite if the probability distribution is zero (see the 6th row in the matrix).
Pretty neat algorithm, right?
In this article I want to separately make the implementation code described bypass. Initialization and filling of the Markov chain do not carry much interest (see the full code at the end).
This algorithm looks particularly simple due to the features of the container discrete_distribution . It’s quite difficult to describe in words how this container works, so let's take as an example the 0th row of our matrix:
0 50 0 0 0 0 50 0 0 0
As a result of the generator operation, it will return either 1 or 6 with probabilities of 0.5 for each. That is, it returns the column number (which is equivalent to the number of the vertex in the chain) where it should continue to move on.
An example of a program that uses the class:
Example output that the program generates:
We see that the algorithm works quite well. As values we can specify anything.
From the illustration of the Markov chain, it is clear that ABDFZ is the most likely sequence of events. She also often appears. Event E is the rarest
The configuration file used in the example:
Thus, we see that the algorithms on graphs are applicable to Markov chains and these algorithms look quite nice. If someone knows a better implementation, then please unsubscribe in the comments.
Full code and readme on github: code
Thank you all for your attention.
I ask under the cat.
Initial knowledge:
Representation of graphs in the form of an adjacency matrix, knowledge of basic concepts about graphs. Knowledge of C ++ for the practical part.
')
Theory
The chain of Markov is a sequence of random events with a finite or countable number of outcomes, characterized by the property that, speaking loosely, with a fixed present, the future is independent of the past. Named in honor of A. A. Markov (senior).
In simple terms, the Markov Chain is a weighted graph. At its vertices are events, and as the weight of the edge connecting vertices A and B is the probability that event A will be followed by event B.
Quite a lot of articles have been written about the use of Markov chains, but we will continue to develop a class.
I will give an example of a Markov chain:
In the following, we will consider this scheme as an example.
Obviously, if there is only one outgoing edge from the vertex A, then its weight will be equal to 1.
Legend
At the vertices we have events (from A, B, C, D, E ...). On the edges there is a probability that after the i-th event there will be an event j> i. For convention and convenience, I numbered the vertices (# 1, # 2, etc.).
The matrix will be called the adjacency matrix of an oriented weighted graph, which we represent the Markov chain. (more on that later). In this particular case, this matrix is also called the matrix of transition probabilities, or simply the transition matrix.
Matrix representation of the Markov chain
We will represent the Markov chains using a matrix, namely, the adjacency matrix with which we represent the graphs.
I recall:
The adjacency matrix of a graph G with a finite number of vertices n (numbered from 1 to n) is a square matrix A of size n, in which the value of the element aij equals the number of edges from the i-th vertex of the graph to the j-th vertex.
Learn more about adjacency matrices in the course of discrete mathematics.
In our case, the matrix will have a size of 10x10, we will write it:
0 50 0 0 0 0 50 0 0 0
0 0 80 20 0 0 0 0 0 0
0 0 0 0 100 0 0 0 0 0
0 0 0 0 100 0 0 0 0 0
0 0 0 0 0 100 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 70 30 0
0 0 0 0 0 0 0 0 0 100
0 0 0 0 0 0 0 0 0 100
0 0 0 0 0 100 0 0 0 0
Idea
Take a closer look at our matrix. In each row we have non-zero values in those columns whose number coincides with the subsequent event, and the non-zero value itself is the probability that this event will occur.
Thus, we have the values of the probability of an event with a number equal to the column number after the event with a number equal to the row .
Those who know probability theory could guess that each line is a probability distribution function.
Markov chain traversal algorithm
1) we initialize the initial position k by the zero vertex.
2) If the vertex is not finite, then we generate the number m from 0 ... n-1 based on the probability distribution in the row k of the matrix, where n is the number of vertices and m is the number of the next event (!). Otherwise we leave
3) The number of the current position k is equal to the number of the generated vertex
4) Step 2
Note: the vertex is finite if the probability distribution is zero (see the 6th row in the matrix).
Pretty neat algorithm, right?
Implementation
In this article I want to separately make the implementation code described bypass. Initialization and filling of the Markov chain do not carry much interest (see the full code at the end).
Implementation of the traversal algorithm
template <class Element> Element *Markov<Element>::Next(int StartElement = -1) { if (Markov<Element>::Initiated) // { if (StartElement == -1) // StartElement = Markov<Element>::Current; // ( Current = 0 ) std::random_device rd; std::mt19937 gen(rd()); std::discrete_distribution<> dicr_distr(Markov<Element>::AdjacencyMatrix.at(Current).begin(), Markov<Element>::AdjacencyMatrix.at(Current).end()); // int next = dicr_distr(gen); // if (next == Markov<Element>::size()) // , , return NULL; Markov<Element>::Current = next; // return &(Markov<Element>::elems.at(next)); // } return NULL; } This algorithm looks particularly simple due to the features of the container discrete_distribution . It’s quite difficult to describe in words how this container works, so let's take as an example the 0th row of our matrix:
0 50 0 0 0 0 50 0 0 0
As a result of the generator operation, it will return either 1 or 6 with probabilities of 0.5 for each. That is, it returns the column number (which is equivalent to the number of the vertex in the chain) where it should continue to move on.
An example of a program that uses the class:
Implementing a program that does a Markov circuit traversal from an example
#include <iostream> #include "Markov.h" #include <string> #include <fstream> using namespace std; int main() { Markov<string> chain; ofstream outs; outs.open("out.txt"); ifstream ins; ins.open("matrix.txt"); int num; double Prob = 0; (ins >> num).get(); // string str; for (int i = 0; i < num; i++) { getline(ins, str); chain.AddElement(str); // } if (chain.InitAdjacency()) // { for (int i = 0; i < chain.size(); i++) { for (int j = 0; j < chain.size(); j++) { (ins >> Prob).get(); if (!chain.PushAdjacency(i, j, Prob)) // { cerr << "Adjacency matrix write error" << endl; } } } outs << chain.At(0) << " "; // 0- for (int i = 0; i < 20 * chain.size() - 1; i++) // 20 { string *str = chain.Next(); if (str != NULL) // outs << (*str).c_str() << " "; // else { outs << std::endl; // , chain.Current = 0; outs << chain.At(0) << " "; } } chain.UninitAdjacency(); // } else cerr << "Can not initialize Adjacency matrix" << endl;; ins.close(); outs.close(); cin.get(); return 0; } Example output that the program generates:
Conclusion
ABDFZ
ACGTZ
ACGTZ
ABDFZ
ACHTZ
ABDFZ
ACGTZ
ACGTZ
ACGTZ
ABDFZ
ABDFZ
ACGTZ
ABDFZ
ABDFZ
ACHTZ
ACGTZ
ACHTZ
ACHTZ
ABEFZ
ACHTZ
ABEFZ
ACGTZ
ACGTZ
ACHTZ
ABDFZ
ABDFZ
ACHTZ
ABDFZ
ACGTZ
ABDFZ
ABDFZ
ABDFZ
ABDFZ
ACGTZ
ABDFZ
ACHTZ
ACHTZ
ABDFZ
ACGTZ
ABDFZ
We see that the algorithm works quite well. As values we can specify anything.
From the illustration of the Markov chain, it is clear that ABDFZ is the most likely sequence of events. She also often appears. Event E is the rarest
The configuration file used in the example:
file
10
A
B
D
E
F
Z
C
G
H
T
0 50.0 0 0 0 0 50 0 0 0
0 0 80.0 20.0 0 0 0 0 0 0
0 0 0 0 100.0 0 0 0 0 0
0 0 0 0 100.0 0 0 0 0 0
0 0 0 0 0 100.0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 70.0 30.0 0
0 0 0 0 0 0 0 0 0 100.0
0 0 0 0 0 0 0 0 0 100
0 0 0 0 0 100.0 0 0 0 0
Conclusion
Thus, we see that the algorithms on graphs are applicable to Markov chains and these algorithms look quite nice. If someone knows a better implementation, then please unsubscribe in the comments.
Full code and readme on github: code
Thank you all for your attention.
Source: https://habr.com/ru/post/302392/
All Articles