Introduction to sequels and macros on Scheme
If you have not heard of call / cc, then you should definitely get acquainted with this powerful tool! Let's talk about the continuation (call / cc) , a simple but difficult to understand construction, which has tremendous power in the right hands . We implement with them the mechanism of yield / next / for ... in , similar to that in Python. Wrap the inside with a macro , another interesting Scheme mechanism.
The article is aimed at novice programmers . Lispery is unlikely to get something new, but I will be grateful for the errors found.

Every programmer periodically encounters insufficient expressiveness of his code, when a simple beautiful idea requires writing hundreds of lines. This has always pushed for the creation of new, more expressive tools such as the OP , with a much greater density of meaning per unit of program text.
')
Continuation (continuation) - is one of the mechanisms that allow the programmer to create such tools on the go. The history of call / cc (call-with-current-continuation, a syntactic construct reflecting the idea of continuations) is closely connected with Scheme , not the most popular language, which, however, has been a source of inspiration for programmers for several decades. Therefore, the narration will be carried out in the Scheme language, and all the code samples are designed to be interpreted using Guile (I am sure that with almost zero effort, I’ll get Racket, Chicken and, probably, one hundred other interpreters of this Lisp dialect).
The sequel is GoTo's strongest brother, an operatorthat cannot be used . Continuation allows:
But why go back to the past?
 Let us explain what has been said in practice:
Let us explain what has been said in practice:
Imagine a piece of the program. Function 1 calls function 2, it calls function 3 from some other variables. Before calling, say, function 2, save the state (called the current context ). Subsequently, at any moment we can return to this context, replacing the result of the function chain
Let's check that everything works really well.
Let's create some spherical example in vacuum. Define the
Result (obvious):
Now save the context before evaluating the condition in the if. Let's see how to do it:
The appearance of call / cc requires the interpreter to take the current context and pass it to the lambda function defined by us inside. The lambda function takes one argument (hereinafter in the texts of the programs we will call it cc - abbreviated from "current continuation"). We can keep this context:
Now we will make magic. Take the saved context, and move on to it. We wrapped the call / cc construct with a condition in the if block, so when we call the context, we need to pass the value that should be returned instead of the calculation
This is done like this:
Here, “Any value” can be placed on any code that returns some value, or this value itself.
Now, if we write:
we will return to the point where the context was received, and everything will look to the code external to the block
Everything works as we wanted, but ... an endless cycle ?! Calmly, all in agreement with the theory. Let's look at how this example works.
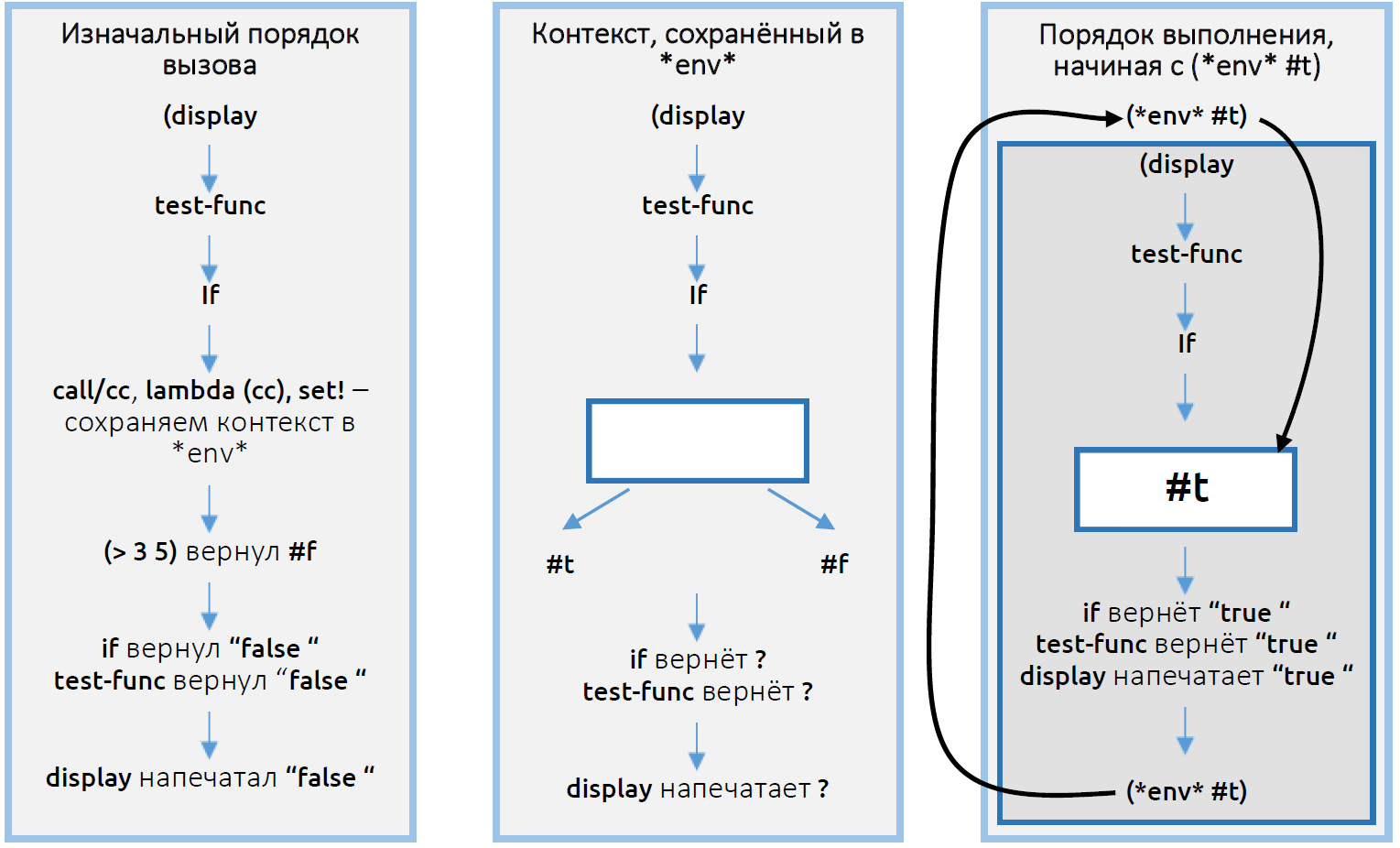
We return to the program state somewhere inside the call stack generated (display ...). There we substitute the #t that is pleasing to us (affecting the result), a safe exit from (display ...) is made, (* env * #t) is called, and in a new way ...
The first acquaintance with call / cc evokes an understanding of the power of this tool, but it is far from immediately obvious how to use it and what can be realized. The classic list of things implemented using call / cc includes loops, loop exit or recursion, loop exit or recursion with return, coroutines, and co-operative multitasking . Thus, continuations can change the flow of program execution in all imaginable ways.
Let's try to use this feature to implement in Scheme the equivalent of generators in Python. We require that the result be as follows:
Perhaps not as concise as in Python, but Scheme is still limited by its syntax (which does not prevent it from being extremely simple and incredibly versatile).
The implementation of the
We realize this by writing an example of a square number generator from 1 to n:
The case is left for small: you need to write something in the variable

We are in some part of the program and we want to go further, forward. But for this you need to get the next value from the generator (box c). We go into the generator (save the state and go up the stairs), select the box and "teleport" back (back to the saved state), but already with the box! In fact, you need to add a couple of lines:
Putting it all together:
Checking:
Hooray! Works!
I hope you noticed one obvious mistake. If we call the received generator more than 10 times, we will enter an infinite loop. Calling
How to do it? Check yourself for understanding, invent yourself (welcome to the comments). Just add one line of code inside
We have achieved the behavior we need. But the syntax is not the same. To create a generator function, we need to wrap it with a lambda function, make a lot of unnecessary gestures ... fortunately, Scheme has a powerful macro mechanism. Macros, as always, are evil, if you cram them everywhere, but if you write once and for a long time, why not make your life easier with beautiful syntactic sugar?
Macros are covered on the Internet much better than the sequels, so only briefly leave them (the second reason is the unexpectedly large size of the article; if the community considers it necessary to have a detailed description of macros in Scheme, I will write the second article).
Probably , it would be wrong to essentially duplicate what was said more than once, including on Habré.
The basics of macros in Scheme (search on page: “Macros”): habrahabr.ru/company/tcsbank/blog/267113
Here we consider the subtlety that will play a significant role.
Let's write an example of a macro that defines a function that simply summarizes the elements of the list (for this, the macro is, of course, not needed; an example, as always, from the air, but necessary for understanding):
Everything is working.
And now let's do this:
Can you imagine in what mess this macro will unfold (due to the coincidence of the names - loop, inside the macro and outside)? Eh, compilation errors will be sprinkled now ... Run ...
Oh really?! How could this work? In fact, in Scheme, a macro is not as straightforward as it seems. In our case, the macro will unfold in:
Macros can define name conflicts outside and inside, so the internal variable
In our case, unfortunately, such intelligence of the macro only interferes. Inside the macro, we will certainly use
To make the macro work the way we need it, there is a more powerful construct,
The article and so it turned out too big, so a detailed description of this tool will be in the next publication (if necessary).
The syntax is similar to
There is an abbreviation for
The previous example will be rewritten as follows (and the code below is equivalent in all senses to code using
You can enter the object identifier from the scope that is external to the macro (from the usual Scheme, so to speak) into the internal scope of the macro using
For example, to ensure that
Scheme offers some syntactic sugar to make this code look nicer:
As a result, we used
Recall the syntax we sought:
Create a macro define-generator, which creates a function of the arguments arg1, arg2 ..., which returns the generator. The code is similar to what we have already written:
Hooray again! Works!
If suddenly you knew a little about the sequels and macros, and I managed to convey to you what is written above, then you can easily write the implementation
Thank you, if you have read to the end. I hope that now Scheme will give someone else some inspiration in our favorite business.
The article is aimed at novice programmers . Lispery is unlikely to get something new, but I will be grateful for the errors found.

What and why
Every programmer periodically encounters insufficient expressiveness of his code, when a simple beautiful idea requires writing hundreds of lines. This has always pushed for the creation of new, more expressive tools such as the OP , with a much greater density of meaning per unit of program text.
')
Continuation (continuation) - is one of the mechanisms that allow the programmer to create such tools on the go. The history of call / cc (call-with-current-continuation, a syntactic construct reflecting the idea of continuations) is closely connected with Scheme , not the most popular language, which, however, has been a source of inspiration for programmers for several decades. Therefore, the narration will be carried out in the Scheme language, and all the code samples are designed to be interpreted using Guile (I am sure that with almost zero effort, I’ll get Racket, Chicken and, probably, one hundred other interpreters of this Lisp dialect).
Part I. Continuations
Start (the essence of the sequels)
The sequel is GoTo's strongest brother, an operator
- Get (capture) the status of the program at the moment
- Save this state (there are other options)
- Return to this state later, whenever you want
But why go back to the past?
- To go forward again, having organized a cycle. This is a rather naive application (in fact, using GoTo).
- To understand the real power of continuations, you need to find out what the “state of the program” mentioned above means. In fact, the current function call stack is saved, that is, the current context . But the next function, which should return the value of the previous one (that is, the one that we actually wrap with the call / cc construct - see below), is not preserved. Later, it can be replaced by another code (in particular, some constant). Imagine that you can return to yourself from the future and pass on to your past any knowledge / material objects / directions for further action!
 Let us explain what has been said in practice:
Let us explain what has been said in practice:Imagine a piece of the program. Function 1 calls function 2, it calls function 3 from some other variables. Before calling, say, function 2, save the state (called the current context ). Subsequently, at any moment we can return to this context, replacing the result of the function chain
(func2 (func3 abc)) value we need, for example, d.Let's check that everything works really well.
First example
Let's create some spherical example in vacuum. Define the
test-func function: ; (define test-func (if (> 3 5) "true " "false ")) (display test-func) (newline) Result (obvious):
>> false Now save the context before evaluating the condition in the if. Let's see how to do it:
(call/cc (lambda (cc) (Some actions))) The appearance of call / cc requires the interpreter to take the current context and pass it to the lambda function defined by us inside. The lambda function takes one argument (hereinafter in the texts of the programs we will call it cc - abbreviated from "current continuation"). We can keep this context:
(define *env* #f) (call/cc (lambda (cc) (begin (set! *env* cc) ; cc, *env* (Some actions)))) Now we will make magic. Take the saved context, and move on to it. We wrapped the call / cc construct with a condition in the if block, so when we call the context, we need to pass the value that should be returned instead of the calculation
(> 3 5) .This is done like this:
(*env* Any_value) Here, “Any value” can be placed on any code that returns some value, or this value itself.
Now, if we write:
(*env* #t) we will return to the point where the context was received, and everything will look to the code external to the block
(call/cc ...) as if the function inside this block (if condition) returned #t!So the result
UPDATE :
Comments gave an understanding that the code(display (*env* #t)) can confuse you. The construction (display ..) in this line will never print anything, because as soon as the interpreter reaches (*env* #t) , an irretrievable transition to another state will be made (more details in the comments). Thus, the operation of the following code does not change from the replacement (display (*env* #t)) to (*env* #t) . (define test-func (if (call/cc (lambda (cc) (begin (set! *env* cc) (> 3 5)) )) "true " "false ")) (display test-func) (display (*env* #t)) (newline) >> false true true true true true true true true true true true true true true true true true true true true true true true true true true true ... Everything works as we wanted, but ... an endless cycle ?! Calmly, all in agreement with the theory. Let's look at how this example works.

We return to the program state somewhere inside the call stack generated (display ...). There we substitute the #t that is pleasing to us (affecting the result), a safe exit from (display ...) is made, (* env * #t) is called, and in a new way ...
We make our own generator
The first acquaintance with call / cc evokes an understanding of the power of this tool, but it is far from immediately obvious how to use it and what can be realized. The classic list of things implemented using call / cc includes loops, loop exit or recursion, loop exit or recursion with return, coroutines, and co-operative multitasking . Thus, continuations can change the flow of program execution in all imaginable ways.
Let's try to use this feature to implement in Scheme the equivalent of generators in Python. We require that the result be as follows:
; (define-generator (generator-func arg1 arg2 ...) (... (yield result) ; ...)) ; . my-gen — : (define my-gen (generator-func 10 30 ...)) (display my-gen) ; (display my-gen) ; ; , (for item in (generator-func 100 70 ...) (display item)) Perhaps not as concise as in Python, but Scheme is still limited by its syntax (which does not prevent it from being extremely simple and incredibly versatile).
First blanks
The implementation of the
yield function is almost obvious. You need to save the current context (to continue with it later), then make a jump to where the generator was called from and replace the generator with the value returned by the yield: (define (yield value) (call/cc (lambda (cc) (set! *env* cc) ; (*return* value)))) ; , , value - It is immediately clear that each generator (there may be several of them in the program) must have its own
*env*and*return*, stored within a certain local scope. - From the first it follows that
yieldcannot be global, which means that it needs to be passed to the function that callsyield
We realize this by writing an example of a square number generator from 1 to n:
(define (create-generator func) (define *env* (lambda () (func yield))) (define *return* #f) (define (yield value) (call/cc (lambda (cc) (set! *env* cc) (*return* value)))) (lambda () ( ))) ; (define (squares-gen n) (lambda (yield) (let loop ((n (+ n 1)) (kn)) (if (> k 0) (begin (yield (expt (- nk) 2)) (loop n (- k 1))))))) Almost done
The case is left for small: you need to write something in the variable
*return* . In order for the generator, once called, to return the value, you need to save the context at the very beginning of the generator, in order to later replace its internal part with the return value. This is what the picture from the beginning of the post says:
We are in some part of the program and we want to go further, forward. But for this you need to get the next value from the generator (box c). We go into the generator (save the state and go up the stairs), select the box and "teleport" back (back to the saved state), but already with the box! In fact, you need to add a couple of lines:
(define (create-generator func) (define ...) ... (lambda () (call/cc (lambda (cc) (set! *return* cc) (*env*))))) ; func, , ; (yield smth) func... ! Result
Putting it all together:
Result
(define (create-generator func) (define *env* (lambda () (func yield))) (define *return* #f) (define (yield value) (call/cc (lambda (cc) (set! *env* cc) (*return* value)))) (lambda () (call/cc (lambda (cc) (set! *return* cc) (*env*))))) ; (define (squares-gen n) (lambda (yield) (let loop ((n (+ n 1)) (kn)) (if (> k 0) (begin (yield (expt (- nk) 2)) (loop n (- k 1))))))) (define my-gen (create-generator (squares-gen 10))) Checking:
; my-gen 7 (let loop ((n 7)) (if (> n 0) (begin (display (my-gen)) (display " ") (loop (- n 1))))) >> 1 4 9 16 25 36 49 Hooray! Works!
Comment
I hope you noticed one obvious mistake. If we call the received generator more than 10 times, we will enter an infinite loop. Calling
(*env*) , we completely return to the state in which we were at the last iteration, because we do not save the new, because we do not reach yield in the code of the generator function. You can do this, for example, as follows: if the generator cannot produce the next value, it returns a stub value, for example, “Stop Iteration” .How to do it? Check yourself for understanding, invent yourself (welcome to the comments). Just add one line of code inside
(define (create-generator func) ...) .Part II. Macros
What for?
We have achieved the behavior we need. But the syntax is not the same. To create a generator function, we need to wrap it with a lambda function, make a lot of unnecessary gestures ... fortunately, Scheme has a powerful macro mechanism. Macros, as always, are evil, if you cram them everywhere, but if you write once and for a long time, why not make your life easier with beautiful syntactic sugar?
Short description
Macros are covered on the Internet much better than the sequels, so only briefly leave them (the second reason is the unexpectedly large size of the article; if the community considers it necessary to have a detailed description of macros in Scheme, I will write the second article).
- The macros in Scheme are similar to the preprocessor in C. Macros are expanded before being translated into bytecode.
- Macros convert syntactic constructs, and only them. We write some lines of code, others are output.
define-syntaxand others like it determine the rules by which the designated conversion occurs.
Probably , it would be wrong to essentially duplicate what was said more than once, including on Habré.
The basics of macros in Scheme (search on page: “Macros”): habrahabr.ru/company/tcsbank/blog/267113
Here we consider the subtlety that will play a significant role.
Let's write an example of a macro that defines a function that simply summarizes the elements of the list (for this, the macro is, of course, not needed; an example, as always, from the air, but necessary for understanding):
; (sum (list 5 9 1 ...)) (define-syntax sum (syntax-rules () ((_ args-list) (let loop ((res 0) (left-list args-list)) (if (not (null? left-list)) (loop (+ res (car left-list)) (cdr left-list)) res))))) (display (sum (list 3 4 5 1))) (newline) >> 13 Everything is working.
And now let's do this:
(define loop (list 3 4 5 1)) (display (sum loop)) Can you imagine in what mess this macro will unfold (due to the coincidence of the names - loop, inside the macro and outside)? Eh, compilation errors will be sprinkled now ... Run ...
>> 13 Oh really?! How could this work? In fact, in Scheme, a macro is not as straightforward as it seems. In our case, the macro will unfold in:
(let loop-1 ((res 0) (left-list loop)) (if (not (null? left-list)) (loop-1 (+ res (car left-list)) (cdr left-list)) res)) Macros can define name conflicts outside and inside, so the internal variable
loop has a different name, loop-1 .Syntax-case, with-syntax, datum-> syntax
In our case, unfortunately, such intelligence of the macro only interferes. Inside the macro, we will certainly use
yield , which will certainly translate to yield-1 .To make the macro work the way we need it, there is a more powerful construct,
syntax-case .The article and so it turned out too big, so a detailed description of this tool will be in the next publication (if necessary).
The syntax is similar to
syntax-rules , the difference in the wrapper is from the lambda function and the way the value is returned, via (syntax something) is a function that returns a syntax structure built from “something”.There is an abbreviation for
(syntax ...) : #' in Scheme.The previous example will be rewritten as follows (and the code below is equivalent in all senses to code using
syntax-rules ):sum via syntax-case
(define-syntax sum (lambda (x) (syntax-case x () ((_ args-list) #'(let loop ((res 0) (left-list args-list)) (if (not (null? left-list)) (loop (+ res (car left-list)) (cdr left-list)) res)))))) You can enter the object identifier from the scope that is external to the macro (from the usual Scheme, so to speak) into the internal scope of the macro using
datum->syntax .For example, to ensure that
yield does not turn into yield-1 inside (syntax ...) , you can do this: (define-syntax sum (lambda (x) (syntax-case x () ((pattern) (syntax-case (datum->syntax x 'yield) () (yield (syntax ... yield ...))))))) Scheme offers some syntactic sugar to make this code look nicer:
(define-syntax sum (lambda (x) (syntax-case x () ((pattern) (with-syntax (yield (datum->syntax x 'yield)) (yield (syntax ... yield ...))))))) As a result, we used
syntax-case to, in fact, create a simple macro in which we can use yield without any problems, and everything will work as we expect.Finally, use macros in
Recall the syntax we sought:
Syntax
; (define-generator (generator-func arg1 arg2 ...) (... (yield result) ; ...)) ; . my-gen -- : (define my-gen (generator-func 10 30 ...)) (display my-gen) ; (display my-gen) ; Create a macro define-generator, which creates a function of the arguments arg1, arg2 ..., which returns the generator. The code is similar to what we have already written:
; : (define-syntax define-generator (lambda (x) ; syntax-case (syntax-case x () ((_ (name . args) body) (with-syntax ((yield (datum->syntax x 'yield))) ; yield (syntax (define (name . args) ; , , (define *env* (lambda () (body))) ; , (define *return* #f) (define (yield value) (call/cc (lambda (cc) (set! *env* cc) (*return* value)))) (lambda () (call/cc (lambda (cc) (set! *return* cc) (*env*))))))))))) (define-generator (squares-gen n) (let loop ((n (+ n 1)) (kn)) (if (> k 0) (begin (yield (expt (- nk) 2)) (loop n (- k 1)))))) (define my-gen (squares-gen 10)) (let loop ((n 7)) (if (> n 0) (begin (display (my-gen)) (display " ") (loop (- n 1))))) >> 1 4 9 16 25 36 49 Hooray again! Works!
Afterword
If suddenly you knew a little about the sequels and macros, and I managed to convey to you what is written above, then you can easily write the implementation
for ... in ... by analogy for ... in ... Do not forget the error intentionally left in the code.Thank you, if you have read to the end. I hope that now Scheme will give someone else some inspiration in our favorite business.
Source: https://habr.com/ru/post/302186/
All Articles