Vacation programmatically, or as I did not participate in the competition for programming on JS. Part two
In the first part of this description of an attempt to solve an interesting competitive problem, I talked about preparing data for analysis and about several experiments. Let me remind you that the condition of the problem was to most likely determine the presence of a word in the dictionary, without having access to this dictionary at the time of the program execution and with a restriction on the program size (including data) in 64K.
Like last time, there is a lot of SQL, JS, as well as neural networks and a Bloom filter under the cat.
Let me remind you that the last experiment described was an attempt to solve the problem through building a decision tree. The next technology tested was the relationship search algorithm included in the Microsoft Data Mining package. Here is the result of his work:
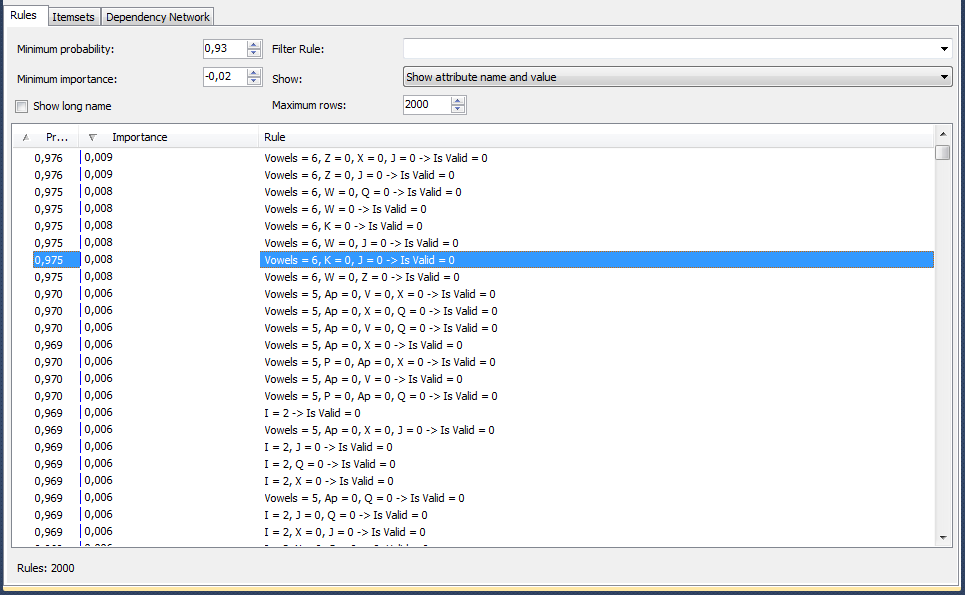
The picture shows that the algorithm shows us that, in his opinion, if the word 6 has vowels and there are no letters "Z", "X" and "J", then with a probability of 97.5% there is no word in the dictionary. Checking how much test data covers all the rules - it turns out that most. I'm happy with the result, take the rules, switch from DataGrip to WebStorm and write JS-code.
The code to check looks like this:
var wordStat=getWordStat(word); var wrongRules=0; var trueRules=0; function getWordStat (word) { // var result={vowels:0,consonants:0}; for (var i=0;i<word.length;i++) { result[word[i]]=result[word[i]]?(result[word[i]]+1):1; if ('aeiouy'.indexOf(word[i])>-1)result.vowels++; else if (word[i]!="'")result.consonants++; } return result; } for (i=0;i<rules.length;i++) { var passed=0; var rulesCount=0; for (var rule in rules[i]){ rulesCount++; if((wordStat[rule.toLowerCase()]?wordStat[rule.toLowerCase()]:0)==rules[i][rule])passed++; } if (passed==rulesCount&&rulesCount!=0) { return false; } } I don’t think about data packing, I’m just building in Excel json type
var rules= [ {"Consonants":6,"H":0,"X":0,"J":0}, {"Consonants":6,"H":0,"V":0,"Q":0} ] Another moment of truth ... And another disappointment - 65%. There is no question about 97.5%.
I check how much data and how it is eliminated by the rules - I get a lot of false negative and false positives. I begin to understand what were my two main "puncture". I did not take into account the repetitions of words and the proportions of arrays. Those.:
1) initially suggested that the probability of testing on test words will coincide with the probability in the test sets. But the words in the test sets are repeated and these repetitions greatly reduce the picture, if I am mistaken on these words. By the way, the thought immediately appears to consider all repeated words to be correct.
2) the mining algorithms did everything correctly: they saw ten thousand correct words for a million wrong words and were delighted with the probability of 99%. I did the wrong thing by feeding the algorithm incommensurable volumes of right and wrong words. For example, check the above rule {"Consonants": 6, "H": 0, "X": 0, "J": 0}:
select isvalid,count(*) from formining10 where Vowels=6 and Z=0 and X=0 and J=0 group by isvalid | isValid | count |
|---|---|
| 0 | 5117424 |
| one | 44319 |
Indeed, the difference is more than 100 times, and the algorithm recognized it correctly. But I can not ignore the 44K correct words, because when checking the proportions will be approximately equal. So, it is necessary to feed the same size arrays of correct and incorrect words. But after all, 600K of incorrect words will not be enough ... I will take another 10M test words, but already with repetitions, i.e. without removing either positive or negative duplicates. The only thing I do is clean the "garbage" through the filters described in the first article (non-existent pairs / triples). I feed the mining ... Alas, he does not find adequate rules in this situation, and when he tries to build a decision tree, he says that he hasn’t found anything good. Let me remind you that I cut off all the "obvious" wrong options even before the mining data was fed through the wrong pairs / triples.
Returning to the "descriptive" method.
Let me remind you that in the first part of an article for mining, I created on the basis of the dictionary a table with a string corresponding to a word, a column — the number of the character in the word, and the cell values is the ordinal number of the letter in the alphabet (27 for the apostrophe). From this table I make a "map" for each length, i.e. for how long on which place this or that letter cannot be found. For example, "7'4" means that in the words of seven letters the apostrophe cannot be the fourth character, and "15b14" means that in the words of the 15 letters "b" has never been seen before the last one.
Create a table with letter positions for each word length.
select length=len(word),'''' letter, charindex('''',word) number into #tmpl from words where charindex('''',word)>0 union select length=len(word),'a' letter, charindex('a',word) number from words where charindex('a',word)>0 ... union select length=len(word),'z' letter, charindex('z',word) number from words where charindex('z',word)>0 Make a Cartesian product of letters, lengths and positions, and then left join existing ones
select l.length,a.letter,l.length from allchars a cross join (select 1 number union select 2 union select 3 union select 20 union select 21) n cross join (select 1 length union select 2 union select 3 union select 20 union select 21) l left join #tmpl t on a.letter=t.letter and t.number=n.number and t.length=l.length where t.letter is not null Next, we supplement the position number in the word "trimmed" half-measure from the first part to check for nonexistent combinations of two and three characters in the word.
Choose pairs and triples:
-- . cright cwrong – . create table stat2(letters char(2),pos int,cright int,cwrong int) create table stat3(letters char(3),pos int,cright int,cwrong int) create table #tmp2(l varchar(2),valid int,invalid int) create table #tmp3(l varchar(3),valid int,invalid int) -- declare @i INT set @i=0 while @i<20 begin set @i=@i+1 truncate table #tmp2 truncate table #tmp3 -- insert into #tmp2 select substring(word,@i,2),0,count(*) from wrongwords where len(word)>@i group by substring(word,@i,2) -- insert into #tmp3 select substring(word,@i,2),count(*),0 from words where len(word)>@i group by substring(word,@i,2) insert into stat2 -- select e.letters2,@i,r.valid,l.invalid from allchars2 e left join #tmp2 l on ll=e.letters2 left join #tmp3 r on rl=e.letters2 end declare @i INT set @i=0 while @i<19 begin set @i=@i+1 truncate table #tmp2 truncate table #tmp3 -- insert into #tmp2 select substring(word,@i,3),0,count(*) from wrongwords where len(word)>@i+1 group by substring(word,@i,3) -- insert into #tmp3 select substring(word,@i,3),count(*),0 from words where len(word)>@i+1 group by substring(word,@i,3) -- insert into stat3 select e.letters3,@i,r.valid,l.invalid from allchars3 e left join #tmp2 l on ll=e.letters3 left join #tmp3 r on rl=e.letters3 print @i end I copy the result to Excel, play with the number in the correct and incorrect words, leaving only the theoretically most likely (found at least in 5-10 words) and the most useful (correct / incorrect ratio at least 1: 300).
I do the pivot table. The result looks like this: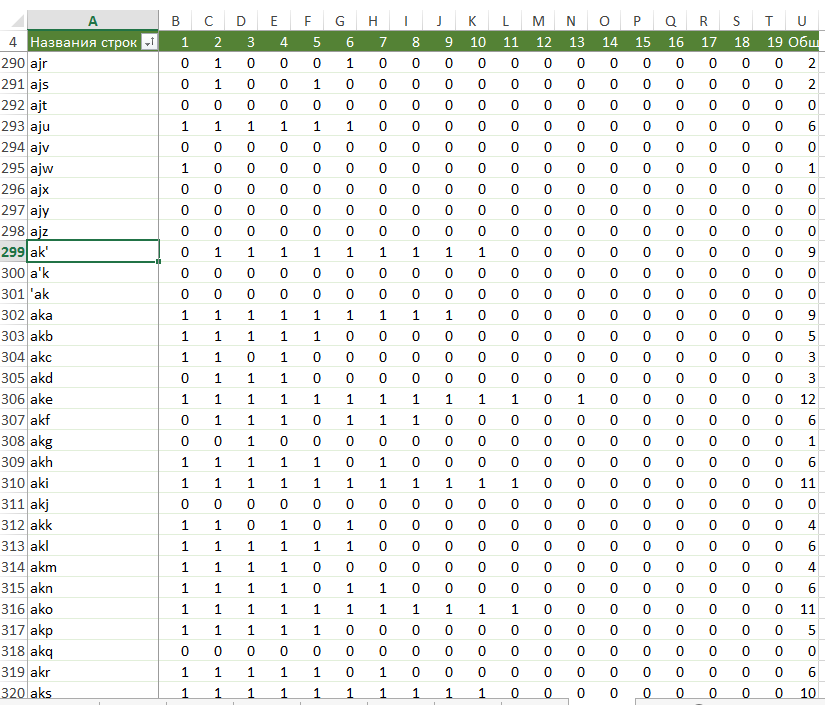
I make the data for the program: pair + bitmask (see the formula at the top of the picture).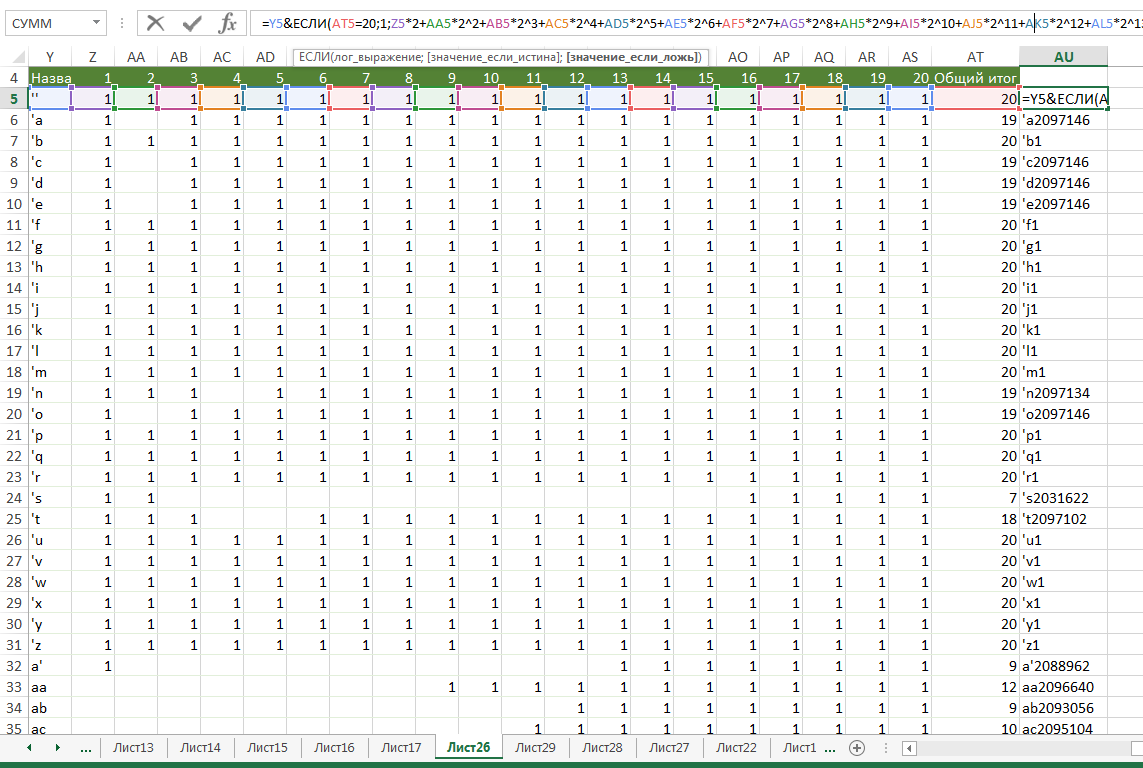
The download code is similar to that described in the first part, but the check is changing.
for (letters in letters2Map) { if (word.indexOf(letters)>=0) { if ((letters2Map[letters] & 1) ==1) { result = return false; } for (var k=0;k<21;k++) { if (((letters2Map[letters] & Math.pow(2,k+1))==Math.pow(2,k+1))&& (letters[0] == word[k-1]) && (letters[1] == word[k])) { return false; } } } } Check: again, no more than 65%. There is a desire to "cheat a little" and improve the result, based on the logic of the generator:
- Treat all repetitions as correct words, since wrong ones repeat much less often. There are some strange clear leaders in repetition among the wrong ones, but they can be simply described as exceptions.
- Monitor the proportions correctly / incorrectly in packages of 100 words and align them after a 60/40 skew.
But both of these options are a) unreliable and b) “unsportsmanlike,” so I leave them for later.
I want to make the last check without restriction on the amount of data to make sure that it is impossible to solve the problem in a descriptive way. To do this, I decide to add all "neighboring" pairs and triples of characters to the checks. I start with the pairs, fill the table:
declare @i INT set @i=0 while @i<17 begin set @i=@i+1 insert into stat2_1 select substring(word,@i,2),substring(word,@i+2,2),@i,count(*),0 from words where len(word)>@i+3 group by substring(word,@i,2),substring(word,@i+2,2) end I save the result simply in the text, I check on the data - the result is about 67%.
It should be borne in mind that if the word is not eliminated as incorrect, the result is considered positive. This means that even 67% is achieved only due to the fact that about half of the words are obviously positive, which means that I eliminate a little more than a third of the wrong words. Since I went through almost all the available options for determining the incorrectness of a word through a combination of letters, I come to the disappointing conclusion that this method can only work as an additional filter, and it is necessary to return to neural networks. Well, it does not work out to create rules for identifying incorrect words like "numismatograph" and "troid".
Since, because of too long training, the options with the presence of incorrect words in the set disappear, I decide to try the Hopfield network . I find the synaptic implementation ready. I test on a small set - the result is surprisingly good. I check the array on all words of 5 characters - the result exceeds 80%. At the same time, the library can even build a function that will check the data without connecting the library itself:
var run = function (input) { F = { 0: 1, 1: 0, ... 370: -0.7308188776194796, ... 774: 8.232535948940295e-7 }; F[0] = input[0]; ... F[26] += F[0] * F[28]; F[26] += F[1] * F[29]; ... F[53] = (1 / (1 + Math.exp(-F[26]))); F[54] = F[53] * (1 - F[53]); F[55] = F[56]; F[56] = F[57]; ... F[773] = (1 / (1 + Math.exp(-F[746]))); F[774] = F[773] * (1 - F[773]); var output = []; output[0] = F[53]; ... output[24] = F[773]; return output; } I am naively happy (once again) and check on the whole array. Let me remind you, in the last part for learning networks I created a table in which words are represented by a sequence of blocks of 5 bits, where each block is a binary representation of the sequence number of a letter in the alphabet. Since the paged data for 21 * 5 input neurons will greatly exceed 64K, I decide to split the long words into two parts and feed each of them.
Learning script:
var synaptic = require('synaptic'); var fs=require('fs'); var Neuron = synaptic.Neuron, Layer = synaptic.Layer, Network = synaptic.Network, Trainer = synaptic.Trainer function hopfield(size) { var input = new synaptic.Layer(size); var output = new synaptic.Layer(size); this.set({ input: input, hidden: [], output: output }); input.project(output, synaptic.Layer.connectionType.ALL_TO_ALL); var trainer = new synaptic.Trainer(this); this.learn = function(patterns) { var set = []; for (var p in patterns) set.push({ input: patterns[p], output: patterns[p] }); return trainer.train(set, { iterations: 50000, error: .000000005, rate: 1, log:1 }); } this.feed = function(pattern) { var output = this.activate(pattern); var pattern = [], error = []; for (var i in output) { error[i] = output[i] > .5 ? 1 - output[i] : output[i]; pattern[i] = output[i] > .5 ? 1 : 0; } return { pattern: pattern, error: error .reduce(function(a, b) { return a + b; }) }; } } hopfield.prototype = new synaptic.Network(); hopfield.prototype.constructor = hopfield; var myPerceptron=new hopfield(11*5+2); var array = fs.readFileSync('formining.csv').toString().split("\n"); var trainingSet=[]; for(i in array) { if (!(i%10000)) console.log(i); var testdata=array[i].split(","); var newtestdata1=[] var newtestdata2=[] var length = parseInt(testdata[0]?1:0); // testdata.splice(0, 1); // , newtestdata1.push(0); for(var j=0;j<11*5;j++){ newtestdata1.push(parseInt(testdata[j]?1:0)?1:0); } if(length>11) { // , newtestdata1.push(1); // "1" , newtestdata2.push(1); for(var j=11*5;j<22*5;j++){ newtestdata2.push(parseInt(testdata[j]?1:0)?1:0); } // "0" , newtestdata2.push(0); } else { // "0" , newtestdata1.push(0); } trainingSet.push(newtestdata1); if(length>11){ trainingSet.push(newtestdata2); } } myPerceptron.learn(trainingSet); The cycle for getting the result is the same, only instead of trainingSet.push there will be a forecast through myPerceptron.activate (newtestdataX) and a bit-by-bit comparison with the last element of the line with the word in which I saved the result (the data file, of course, will also be different - with adding the wrong words).
I check.
Catastrophe.
Not a single correct answer. More precisely, all questions get a positive response. Returning to a set of five characters. Works fine. I remove the second part of the word - it still does not work as it should. By experimenting, I stumble upon a strange feature: the array on five characters works fine exactly until I mix it up. That is, the algorithm is well trained solely due to the good location of the stars. In any other situation on a large amount of data, regardless of the settings, this particular algorithm selects the factors in such a way that they give a positive answer with almost any data set.
Once again I get upset. Only a day remained until the end of the contest, but I decide to continue the search. Stumble upon a bloom filter . I put a deliberately large size (10,000,000). I check. 95%. Hooray! I reduce to a million - the result worsens to 81%. I decide to replace the words with their hash :
function bitwise(str){ var hash = 0; if (str.length == 0) return hash; for (var i = 0; i < str.length; i++) { var ch = str.charCodeAt(i); hash = ((hash<<5)-hash) + ch; hash = hash & hash; // Convert to 32bit integer } return hash; } function binaryTransfer(integer, binary) { binary = binary || 62; var stack = []; var num; var result = ''; var sign = integer < 0 ? '-' : ''; function table (num) { var t = '0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ'; return t[num]; } integer = Math.abs(integer); while (integer >= binary) { num = integer % binary; integer = Math.floor(integer / binary); stack.push(table(num)); } if (integer > 0) { stack.push(table(integer)); } for (var i = stack.length - 1; i >= 0; i--) { result += stack[i]; } return sign + result; } function unique (text) { var id = binaryTransfer(bitwise(text), 61); return id.replace('-', 'Z'); } The result was 88%. I upload data - a lot. I think how to reduce. Reduce the size of the filter to 500,000 - the result worsens to 80%. I suppose you need to reduce the number of words.
The logical first step is to remove more than 100K duplicate words with "'s". But I would like to do something more substantial. I will not list all the tested options for reducing the dictionary, I’ll dwell on the last one I chose as a worker:
The basic idea is to remove words from the dictionary that are already contained in other words, but with prefixes and endings, and add a bit mask to the absorbing words, which will say whether the correct words are the same as this, but without first / last 1/2/3/4 letters. Then at the time of verification we will take the word and try it with all possible prefixes and endings.
For example (option with "'s"), the word "sucralfate's4" means that the word "sucralfate" still exists, and the word "suckstone16" means that there is also the word "stone", and "suctorian's12" means that both "suctorian" and "suctoria" will also be correct.
It remains only a little - to figure out how to create such a directory. The result is the following algorithm:
We make tables with prefixes and endings
select word,p=substring(word,len(word),1),w=substring(word,1,len(word)-1) into #a1 from words where len(word)>2 select word,p=substring(word,1,1),w=substring(word,2,len(word)-1) into #b1 from words where len(word)>2 select word,p=substring(word,len(word)-1,2),w=substring(word,1,len(word)-2) into #a2 from words where len(word)>3 select word,p=substring(word,len(word)-2,3),w=substring(word,1,len(word)-3) into #a3 from words where len(word)>4 select word,p=substring(word,len(word)-3,4),w=substring(word,1,len(word)-4) into #a4 from words where len(word)>5 select word,p=substring(word,1,2),w=substring(word,3,len(word)-2) into #b2 from words where len(word)>3 select word,p=substring(word,1,3),w=substring(word,4,len(word)-3) into #b3 from words where len(word)>3 select word,p=substring(word,1,4),w=substring(word,5,len(word)-4) into #b4 from words where len(word)>4 General table for the result
select word, substring(word,len(word),1) s1, substring(word,1,len(word)-1) sw1, substring(word,len(word)-1,2) s2, substring(word,1,len(word)-2) sw2, substring(word,len(word)-2,3) s3, substring(word,1,len(word)-3) sw3, IIF(len(word)>4,substring(word,len(word)-3,4),'') s4, IIF(len(word)>4,substring(word,1,len(word)-4),'') sw4, substring(word,1,1) p1,substring(word,2,len(word)-1) pw1, substring(word,1,2) p2,substring(word,3,len(word)-2) pw2, substring(word,1,3) p3,substring(word,4,len(word)-3) pw3, IIF(len(word)>4,substring(word,1,4),'') p4,IIF(len(word)>4,substring(word,5,len(word)-4),'') pw4, se1=null,se2=null,se3=null,se4=null,pe1=null,pe2=null,pe3=null,pe4=null,excluded=0 into #tmpwords from words where len(word)>2 Indices not to wait forever
create index a1 on #tmpwords(word) create index p0 on #tmpwords(s1) create index p1 on #tmpwords(sw1) create index p2 on #tmpwords(s2) create index p3 on #tmpwords(sw2) create index p4 on #tmpwords(s3) create index p5 on #tmpwords(sw3) create index p6 on #tmpwords(s4) create index p7 on #tmpwords(sw4) create index p20 on #tmpwords(p1) create index p30 on #tmpwords(pw1) create index p21 on #tmpwords(p2) create index p31 on #tmpwords(pw2) create index p41 on #tmpwords(p3) create index p51 on #tmpwords(pw3) create index p61 on #tmpwords(p4) create index p71 on #tmpwords(pw4) We count and save the number of words with each prefix and the end of each length:
select p into #a11 from #a1 a join words w on w.word=aw and len(w.word)>2 group by p having count(*)>1 select p into #a21 from #a2 a join words w on w.word=aw and len(w.word)>2 group by p having count(*)>1 select p into #a31 from #a3 a join words w on w.word=aw and len(w.word)>2 group by p having count(*)>1 select p into #a41 from #a4 a join words w on w.word=aw and len(w.word)>2 group by p having count(*)>1 select p into #b11 from #b1 a join words w on w.word=aw and len(w.word)>2 group by p having count(*)>1 select p into #b21 from #b2 a join words w on w.word=aw and len(w.word)>2 group by p having count(*)>1 select p into #b31 from #b3 a join words w on w.word=aw and len(w.word)>2 group by p having count(*)>1 select p into #b41 from #b4 a join words w on w.word=aw and len(w.word)>2 group by p having count(*)>1 Mark the words absorbers in the table with the result
update w set se1=1 from #tmpwords w join #a11 a on ap=w.s1 join #tmpwords t on t.word=w.sw1 update w set se2=1 from #tmpwords w join #a21 a on ap=w.s2 join #tmpwords t on t.word=w.sw2 update w set se3=1 from #tmpwords w join #a31 a on ap=w.s3 join #tmpwords t on t.word=w.sw3 update w set se4=1 from #tmpwords w join #a41 a on ap=w.s4 join #tmpwords t on t.word=w.sw4 update w set pe1=1 from #tmpwords w join #b11 a on ap=w.p1 join #tmpwords t on t.word=w.pw1 update w set pe2=1 from #tmpwords w join #b21 a on ap=w.p2 join #tmpwords t on t.word=w.pw2 update w set pe3=1 from #tmpwords w join #b31 a on ap=w.p3 join #tmpwords t on t.word=w.pw3 update w set pe4=1 from #tmpwords w join #b41 a on ap=w.p4 join #tmpwords t on t.word=w.pw4 Create a combined result in order to select the most frequent options.
select s1 p,count(*) cnt into #suffixes from #tmpwords where se1 is not NULL group by s1 union all select s2,count(*) from #tmpwords where se2 is not NULL group by s2 union all select s3,count(*) from #tmpwords where se3 is not NULL group by s3 union all select s4,count(*) from #tmpwords where se4 is not NULL group by s4 select p1,count(*) cnt into #prefixes from #tmpwords where pe1 is not NULL group by p1 union all select p2,count(*) from #tmpwords where pe2 is not NULL group by p2 union all select p3,count(*) from #tmpwords where pe3 is not NULL group by p3 union all select p4,count(*) from #tmpwords where pe4 is not NULL group by p4 We leave only those that occur in more than 100 words.
select *,'s' type ,IIF(cnt>100,0,1) excluded into #result from #suffixes union all select *,'p' type, IIF(cnt>100,0,1) excluded from #prefixes Reset statistics
update #tmpwords set se1=null,se2=null,se3=null,se4=null,pe1=null,pe2=null,pe3=null,pe4=null Remove the "extra" consoles and endings
delete a from #a11 a join #result r on rp=ap and r.type='s' and excluded=1 delete a from #a21 a join #result r on rp=ap and r.type='s' and excluded=1 delete a from #a31 a join #result r on rp=ap and r.type='s' and excluded=1 delete a from #a41 a join #result r on rp=ap and r.type='s' and excluded=1 delete a from #b11 a join #result r on rp=ap and r.type='p' and excluded=1 delete a from #b21 a join #result r on rp=ap and r.type='p' and excluded=1 delete a from #b31 a join #result r on rp=ap and r.type='p' and excluded=1 delete a from #b41 a join #result r on rp=ap and r.type='p' and excluded=1 Update statistics for the remaining most frequently encountered.
update w set se1=1 from #tmpwords w join #a11 a on ap=w.s1 join #tmpwords t on t.word=w.sw1 update w set se2=1 from #tmpwords w join #a21 a on ap=w.s2 join #tmpwords t on t.word=w.sw2 update w set se3=1 from #tmpwords w join #a31 a on ap=w.s3 join #tmpwords t on t.word=w.sw3 update w set se4=1 from #tmpwords w join #a41 a on ap=w.s4 join #tmpwords t on t.word=w.sw4 update w set pe1=1 from #tmpwords w join #b11 a on ap=w.p1 join #tmpwords t on t.word=w.pw1 update w set pe2=1 from #tmpwords w join #b21 a on ap=w.p2 join #tmpwords t on t.word=w.pw2 update w set pe3=1 from #tmpwords w join #b31 a on ap=w.p3 join #tmpwords t on t.word=w.pw3 update w set pe4=1 from #tmpwords w join #b41 a on ap=w.p4 join #tmpwords t on t.word=w.pw4 Mark "absorbed" words
update t set excluded=1 from #tmpwords w join #a11 a on ap=w.s1 join #tmpwords t on t.word=w.sw1 update t set excluded=1 from #tmpwords w join #a11 a on ap=w.s1 join #tmpwords t on t.word=w.sw1 update t set excluded=1 from #tmpwords w join #a21 a on ap=w.s2 join #tmpwords t on t.word=w.sw2 update t set excluded=1 from #tmpwords w join #a31 a on ap=w.s3 join #tmpwords t on t.word=w.sw3 update t set excluded=1 from #tmpwords w join #a41 a on ap=w.s4 join #tmpwords t on t.word=w.sw4 update t set excluded=1 from #tmpwords w join #b21 a on ap=w.p2 join #tmpwords t on t.word=w.pw2 update t set excluded=1 from #tmpwords w join #b31 a on ap=w.p3 join #tmpwords t on t.word=w.pw3 update t set excluded=1 from #tmpwords w join #b41 a on ap=w.p4 join #tmpwords t on t.word=w.pw4 Profit :-)
select excluded,count(*) cnt from #tmpwords group by excluded | excluded | cnt |
|---|---|
| 0 | 397596 |
| one | 232505 |
The directory shrank to 23,2505 lossless entries.
Now we need to make a check. It became very complicated and slowed down due to the need to iterate through all possible prefixes and endings:
// result=bloom.test(unique(word)) if(result){ return true; } // for(var i=0;i<255;i++) { // - result=bloom.test(unique(word+i)) if(result){ return true; } // for (var part in parts ){ //1-,2- var testword=(parts[part]==2?part:"")+word+(parts[part]==1?part:""); // , 4 bitmask=Math.pow(2,(parts[part]-1)*4+part.length); // if(i&bitmask==bitmask){ result=bloom.test(unique(testword+i)) if (result){ return true } } } I run. The result has worsened. But he had to improve! There is no time left, the debugger on the webstorm is terribly buggy, I don’t have time to figure it out. There is no sense to send what is, but it was interesting. I hope you do too. "Holiday" ends, it's time to go back to my sheep your project . Thanks for attention.
')
Source: https://habr.com/ru/post/302066/
All Articles