Application of statistical criteria for solving detection problems in radio engineering

annotation

The article describes the basics of statistical signal processing and methods for their optimal processing * against the background of noise.

Introduction

The main task of radio engineering is receiving, transmitting and processing information using a radio signal as a carrier. The main requirement for radio systems is to receive timely and reliable information from the source to the consumer. However, this is hampered by the physics of the principles of operation of transceiver devices and the signal propagation medium, the essence of which is the fluctuation of the physical parameters of the system and the random value of the received signal having a noise component, also related to stochastic processes.
')
At the moment, the most effective way to distinguish between useful signals in the background of noise and interference is the optimal processing, implemented, as a rule, by comparing the received input realization with the a priori known form of the useful signal. At the same time, the noise, which by its nature is a weakly correlated process, makes a smaller contribution to the value, which shows the degree of this comparison and is called the correlation coefficient. Thus, any detection task is reduced to testing at least two hypotheses. In the general case, the detection task consists of two hypotheses: H_0 - the signal is absent at the input of the receiving device, H_1 - the signal is present at the input of the receiving device. Different detection algorithms provide different probabilities of correct detection P {d_1 / H_1} with various other statistical parameters. There are criteria for comparing the effectiveness of detection algorithms, and since probabilistic values ​​are processed, the nature of these criteria is statistical. In other words, the criterion can be defined as a measure of comparison.

Statistical detection criteria

Most radar target detection algorithms include the following steps:

1. Reception input implementation
2. Formation of the threshold based on a priori or a posteriori information.
3. Optimal filtering of the input implementation
4. Decision on signal / target availability

In this case, the sequence of receiving the input implementation and the formation of the threshold depends directly on the type of algorithm. Algorithms that form a threshold based on a posteriori information about the accepted input implementation are called adaptive [1]. The criterion is chosen empirically based on the type of task. For example: when choosing a place of work, two criteria are usually considered:

• The maximum ratio of money earned to the power spent.
• Maximum pleasure received from work.

Unfortunately, modern realities put such a specialist in priority, whose skills would enable us to launch products as soon as possible and maximize the company's profits. And often the second criterion is either discarded, or when analyzing the situation, it is assigned a low priority. The indicator, in this case, determining the priority of the criteria, is called its power.

In mathematical statistics, the power of a criterion is defined as the probability of not making a second kind error when making a decision. In our case, the error of the second kind is not getting settled on the work that is optimal for oneself; in the general case, this is a false assumption that the event corresponds to the H_0 hypothesis is true.

Of course, there are no universal criteria. For example, the criterion that has the greatest power in solving one problem, in solving another, may turn out to be the worst in this indicator.

The criterion of minimum average risk (Bayes criterion)

Fig. 1. Graph of the distribution of the conditional probability density of the presence of W (U | A = 1) and the absence of W (U | A = 0) with error probabilities

Let A = 1 correspond to the presence of the s (t) signal, and A = 0 to its absence. The set of solutions d degenerates into two: d_0 → A = 1 and d_1 → A = 0.
When solving a binary detection problem, the problem is equivalent to testing the hypothesis H_1 that A = 1, with the alternative hypothesis H_0 that A = 0, and the loss function goes into a square matrix:



Thus, the conditional risk with A = 0 is r_0 = C_00 P {d_0 / H_0} + C_01 P {d_1 / H_0} = C_00 (1-P {d_1 / H_0}) + C_01 P {d_1 / H_0}, and for A = 1 is equal to r_1 = C_10 P {d_0 / H_1} + C_11 P {d_1 / H_1} = C_10 (1-P {d_1 / H_1}) + C_11 P {d_1 / H_1}, where P {d_1 / H_1} - the probability of correct detection, and P {d_1 / H_0} is the probability of a false alarm.

The average risk is defined as r ̅ = qr_0 + pr_1, where q is the a priori probability of the absence of a signal, and p is the a priori probability of the presence of a signal and determines the average loss during a false alarm and the omission of the target [2]. For example: when using such a criterion to set a threshold for triggering a fire alarm, the cost of risk in case of a false alarm is a call to the fire service, and in case of a pass, the cost of things in a burnt apartment or office.

Figure 1 illustrates the graphs of the probability density distribution in the presence and absence of a signal, and the areas whose area is numerically equal to the error probabilities when making a decision are also highlighted. Due to the stochastic nature of the phenomena considered in this example, the distributions have non-zero dispersion. According to the minimum average risk criterion, the best signal detection algorithm will be the one with the minimum r ̅ [2].

A posteriori maximum probability criterion (maximum likelihood)

This criterion is obtained from the criterion of the minimum average risk, provided that the losses during an error are inversely proportional to the probability of their occurrence C_01 = 1 / P {d_0}, C_10 = 1 / P {d_1}. In this case, the threshold of the optimal detector is set in such a way as to minimize the sum of the error probabilities P_osh = P {d_0 / H_1} + P {d_1 / H_0} (see Fig.2).


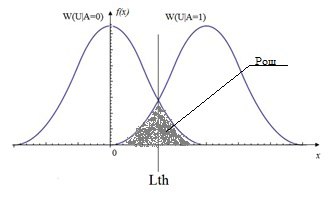
Fig.2 Graph of the distribution of the conditional probability density of the presence of W (U | A = 1) and the absence of W (U | A = 0) with the probability of error

Two-threshold Wald criterion

In cases where the monitoring of the process plays an important role, for example, if there are several channels and one detector or a radar survey, the criterion of the successive testing of Wald's hypotheses, also known as the two threshold, is used.


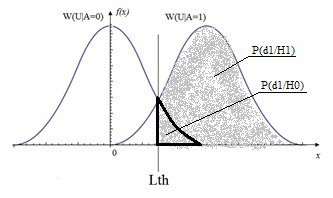
Fig.3 Graph of the distribution of the conditional probability density of the presence of W (U | A = 1) and the absence of W (U | A = 0) with the probability of correct detection and the probability of false alarm

According to this criterion, the probability domain is divided into three subregions divided by two thresholds determined by the probabilities of correct detection and false alarm (see Figure 3):
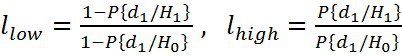
The Wald criterion is optimal in the sense of minimizing the average observation time for a large number of experiments [4]. Since the most preferable for radar is to reduce the duration of the detection procedure, modern realities lead to an increasingly active use of this criterion [5].

Neumann-Pearson criterion

A big minus of the Bayesian class criteria is the need for a priori knowledge of the elements of the loss matrix. For example: if an enemy bomber passes into Union territory, the cost of risks cannot be calculated.

The Neumann-Pearson criterion records the detection time. The algorithm with the maximum probability of correct detection P {d_1 / H_1} is optimal, provided that the probability of a false alarm P {d_1 / H_0} does not exceed a given value [6].

In view of the fact that the Neumann-Pearson criterion does not require knowledge of a priori probabilities of situations A = 1 and A = 0, it is used in radar as one of the main ones [5].

Conclusion

When developing detectors, it is very important to consciously choose the optimality criterion, because, as mentioned earlier, each criterion has maximum power in any particular situation and the use of others can lead to undesirable consequences.

List of sources used:

[1] Bulyakulov RR The adaptive threshold device. P.165.
doi: 10.1109 / EIConRusNW.2016.7448237
[2] Bakulev, P.A. Radar systems. Textbook for universities / P.A. Bakulev; M .: Radio engineering, 2004. - 46 p.
[3] Yurevich, E.I. The theory of automatic control / E.I. Yurevich; M .: Energy, 1969
[4] Bogatyrev, A.A. Standardization of statistical methods of quality management / A. A. Bogatyrev, Yu. D. Filippov; M .: Publishing House of Standards, 1989. - 42 p.
[5] Khramenkov, A.S. Comparative analysis of radar detectors based on the Neumann-Pierson criterion and the consistent probability ratio criterion / .. Khramenkov, S.N. Yarmolik // reports of BSUIR №6 (76) Minsk, 2013.
[6] Vasiliev, K.K. Signal Processing Techniques: Tutorial / K.K. Vasiliev; Ulyanovsk, 2001.