We clean the bow (but not crying): optimization techniques
This article is a formal response to posting on the IDZ forum . The problem that the author of the original publication described was that the performance of the code did not increase sufficiently when using OpenMP on an 8-core E5-2650 V2 processor with 16 hardware threads. It took some time on the forum to help the publication author and provide him with the necessary hints, however, there was not enough time to optimize the code. This article describes further optimization techniques in addition to those described on the IDZ forum.

I must say that I do not know the skill level of the author of the original publication. I will proceed from the fact that the author recently graduated from an educational institution where they could teach parallel programming with an emphasis on scaling. In practice, more often it happens that systems have a limited amount of computing resources (threads), so you should remember not only about scaling, but also about efficiency. The source code example published on the forum contains basic information that helps to understand how to solve the problems of efficiency (to a greater extent) and scaling (to a lesser extent).
When preparing the code for this article, I took the liberty to rework the sample code, retaining its overall design and layout. I saved the basic algorithm unchanged, because the sample code was taken from the application, which could have other functions in addition to the algorithm described. In the sample code provided, a LOGICAL array (mask) was used to control the flow. A sample of the code could have been written without logical arrays, but this code could be a fragment of a larger application, in which these arrays of masks could be necessary for some reason not so obvious in the sample code. Therefore, I left the mask in place.
')
Having studied the code and the first attempt of parallelization, I determined that the most optimal place was not chosen for creating a parallel region (parallel DO). The source code looks like this.
At the first attempt of parallelization, the user applied it to the do j = loop. This is the most intense level of the cycle, but to solve this problem on this platform you need to work at another level.
In this case, 16 threads were used. Two inner cycles together perform 8100 iterations, which gives approximately 506 iterations per stream (if we have 16 threads). Nevertheless, the entry into the parallel region is carried out 120 times (60 * 2). The work done in the innermost cycle did not matter much, but it required resources. Because of this, the parallel region has covered a large part of the application. With 16 threads and 60 iterations of the outer loop counter (120 when using loops), it is more efficient to create a parallel region in the do k loop.
The code has been modified to perform a do k loop many times and calculate the average execution time of the entire do k loop. When applying optimization techniques, you can use the difference between the average operation time of the source code and the revised code to measure the improvements achieved. I do not have an 8-core E5-2650 v2 processor for testing, but I found a 6-core E5-2620 v2 processor. The slightly revised code produced the following results:
On a 6-core E5-2620 v2 processor, the performance increase should be somewhere between six times and twelve times (if we take into account an additional 15% for hyper-threading, then the speed should increase 7 times). Increased productivity by 4.74 times. Significantly less than expected: we expected a sevenfold acceleration.
In further sections of this article we will look at other optimization techniques.
Note that the ParallelAtInnerTwoLoops report indicates that in the second run, the multiplier was different from the multiplier of the first run. The reason for this behavior is in the successful placement of the code (or in the wrong one). The code itself did not change, it is completely identical in both launches. The only difference is in adding additional code and in inserting call statements into these routines. It is important to remember that placing tight cycles can greatly affect the performance of these cycles. In some cases, code performance may change significantly even if a single operator is added.
To make it easier to read code changes, the text of the three inner loops was enclosed in a subroutine. Due to this, it becomes easier to study the code and carry out diagnostics using the VTune profiler. An example from the ParallelAtkmLoop subroutine:
The first stage of optimization includes two changes.
As a result of these two changes, the performance increased by 2.46 times compared with the initial attempt to parallelize. This is a good result, but is it worth staying there?
In the innermost loop, we see the following:
It turns out that each iteration has a different amount of work. In this case, it is better to use dynamic planning. The next stage of optimization is applied to ParallelAtkmLoopDynamic . This is the same code as ParallelAtkmLoop , but with the addition of schedule (dynamic) to ! $ Omp do .
This simple change alone resulted in a speed increase of 1.25 times. Note that dynamic scheduling is not the only possible planning method. There are other types worth exploring. Also remember that for this type of planning a modifier (fragment size) is often added.
The next level of optimization, which provides an acceleration of 1.52 times, can be called aggressive optimization. To achieve this incremental speed increase of 52%, tangible programming efforts are required (however, nothing prohibitively complex). The possibility of this optimization is determined by analyzing the assembler code in VTune.
It should be emphasized that there is no need to understand assembly code for its analysis. As a rule, one can proceed from the following:
the more assembler code, the lower the performance.
You can draw a direct parallel: the harder (more complex) the assembler code, the more likely that the compiler will miss the optimization possibilities. If you see missing opportunities, you can use a simple technique to help the compiler optimize the code.
In the code of the main algorithm we see.
Let's start Intel Amplifier (VTune) and as an example we will consider line 540.

This is part of the instruction that multiplies two numbers. For this partial information you can expect:
If you click the Assembly button in the Amplifier.
Then we sort by line number of the code.
In line of code 540 we see the following.
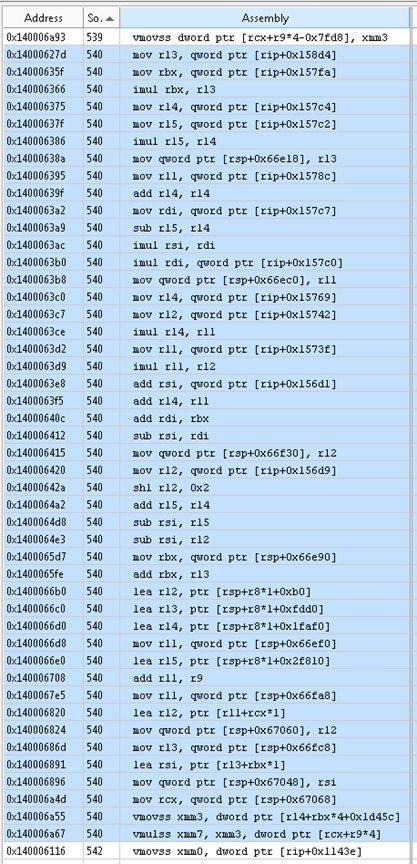
A total of 46 assembly instructions are used to multiply two numbers.
We now turn to mutual influence.
These two numbers are cells of two arrays. The SLX array has six subscriptions, the other array has one. The last two assembler instructions: vmovss from memory and vmulss from memory. We hoped to get a fully optimized code that met our expectations. In the above code, 44 out of 46 assembler functions are associated with the calculation of array indices for these two variables. Naturally, several instructions may be required to obtain indices in arrays, but 44 is clearly too many. Is it possible to reduce the complexity in any way?
When viewing the source code (the latest version shown above), you can see that the last two subordinate SLX scripts and one subordinate dz script are invariant for the two most internal loops. In the case of SLX, the left of two indices (two variables controlling the most internal loops) is a continuous array fragment. The compiler did not recognize the constant (right) array indices as candidates for an invariant loop code that can be inferred from the loop. In addition, the compiler could not recognize the two indices, located to the left of all, to collapse into one index.
This is a good example of possible optimization that can be implemented by the compiler. In this case, the following optimization procedure, in which invariant subordinate scenarios are derived from the cycle, provides an increase in productivity by 1.52 times.
We now know that much of the do code includes contiguous array fragments with several subordinate scripts. Is it possible to reduce the number of subordinate scenarios without rewriting the entire application?
Answer: yes, it is possible if you encapsulate smaller sections of arrays represented by a smaller number of subordinate scripts. How to do this in our code example?
I decided to apply this approach to two levels of nesting.
The outermost layer transmits fragments of the bid level array.
Note that for arrays without pointers (distributed or with fixed sizes) arrays are continuous. This makes it possible to “cut off” the rightmost indices for transmitting a fragment of a continuous array, for which you simply need to calculate the offset in a subset of a larger array. At the same time, in order to try to “cut off” any other indices, except the rightmost ones, you need to create a temporary array, which should be avoided. However, in some cases, even this may be appropriate.
At the second nested level, we have expanded the additional index of the array of the do k loop, and also compressed the first two indices into one.
Notice that a fragment of a continuous array is transmitted at the call point (link). Empty arguments to the procedure being called indicate a continuous chunk of memory of the same size with a different set of indices. If you are careful when working in FORTRAN, it is quite feasible.
All actions to create code are reduced to copy and paste operations, and then to search and replace. Except for this, the code flow does not change. This could be done by an attentive novice programmer who has the necessary instructions.
In future versions of the compiler, built-in optimization tools may make all these actions unnecessary, but now “unnecessary” programming can in some cases lead to a significant increase in performance (in this case by 52%).
Equivalent instruction is now such.

The assembler code now looks like this.

Instead of 46 instructions, 6 is left, that is, 7.66 times less. Thus, reducing the number of subordinate scripts in the array allows you to reduce the number of instructions.
The introduction of a two-level investment with "cutting" led to an increase in productivity by 1.52 times. Is 52% more productivity worth the extra effort? Decide for yourself, everything is subjective here. It can be assumed that optimization algorithms incorporated in future versions of compilers will themselves extract subordinate scripts of invariant arrays, which was done manually above. But for now you can use the described method of "cutting" and compressing indexes.
I hope my recommendations will be helpful.
» Sample source code

I must say that I do not know the skill level of the author of the original publication. I will proceed from the fact that the author recently graduated from an educational institution where they could teach parallel programming with an emphasis on scaling. In practice, more often it happens that systems have a limited amount of computing resources (threads), so you should remember not only about scaling, but also about efficiency. The source code example published on the forum contains basic information that helps to understand how to solve the problems of efficiency (to a greater extent) and scaling (to a lesser extent).
When preparing the code for this article, I took the liberty to rework the sample code, retaining its overall design and layout. I saved the basic algorithm unchanged, because the sample code was taken from the application, which could have other functions in addition to the algorithm described. In the sample code provided, a LOGICAL array (mask) was used to control the flow. A sample of the code could have been written without logical arrays, but this code could be a fragment of a larger application, in which these arrays of masks could be necessary for some reason not so obvious in the sample code. Therefore, I left the mask in place.
')
Having studied the code and the first attempt of parallelization, I determined that the most optimal place was not chosen for creating a parallel region (parallel DO). The source code looks like this.
bid = 1 ! { not stated in original posting, but would appeared to be in a DO bid=1,65 } do k=1,km-1 ! km = 60 do kk=1,2 !$OMP PARALLEL PRIVATE(I) DEFAULT(SHARED) !$omp do do j=1,ny_block ! ny_block = 100 do i=1,nx_block ! nx_block = 81 ... {code} enddo enddo !$omp end do !$OMP END PARALLEL enddo enddo At the first attempt of parallelization, the user applied it to the do j = loop. This is the most intense level of the cycle, but to solve this problem on this platform you need to work at another level.
In this case, 16 threads were used. Two inner cycles together perform 8100 iterations, which gives approximately 506 iterations per stream (if we have 16 threads). Nevertheless, the entry into the parallel region is carried out 120 times (60 * 2). The work done in the innermost cycle did not matter much, but it required resources. Because of this, the parallel region has covered a large part of the application. With 16 threads and 60 iterations of the outer loop counter (120 when using loops), it is more efficient to create a parallel region in the do k loop.
The code has been modified to perform a do k loop many times and calculate the average execution time of the entire do k loop. When applying optimization techniques, you can use the difference between the average operation time of the source code and the revised code to measure the improvements achieved. I do not have an 8-core E5-2650 v2 processor for testing, but I found a 6-core E5-2620 v2 processor. The slightly revised code produced the following results:
OriginalSerialCode Average time 0.8267E-02 Version1_ParallelAtInnerTwoLoops Average time 0.1746E-02, x Serial 4.74 On a 6-core E5-2620 v2 processor, the performance increase should be somewhere between six times and twelve times (if we take into account an additional 15% for hyper-threading, then the speed should increase 7 times). Increased productivity by 4.74 times. Significantly less than expected: we expected a sevenfold acceleration.
In further sections of this article we will look at other optimization techniques.
OriginalSerialCode Average time 0.8395E-02 ParallelAtInnerTwoLoops Average time 0.1699E-02, x Serial 4.94 ParallelAtkmLoop Average time 0.6905E-03, x Serial 12.16, x Prior 2.46 ParallelAtkmLoopDynamic Average time 0.5509E-03, x Serial 15.24, x Prior 1.25 ParallelNestedRank1 Average time 0.3630E-03, x Serial 23.13, x Prior 1.52 Note that the ParallelAtInnerTwoLoops report indicates that in the second run, the multiplier was different from the multiplier of the first run. The reason for this behavior is in the successful placement of the code (or in the wrong one). The code itself did not change, it is completely identical in both launches. The only difference is in adding additional code and in inserting call statements into these routines. It is important to remember that placing tight cycles can greatly affect the performance of these cycles. In some cases, code performance may change significantly even if a single operator is added.
To make it easier to read code changes, the text of the three inner loops was enclosed in a subroutine. Due to this, it becomes easier to study the code and carry out diagnostics using the VTune profiler. An example from the ParallelAtkmLoop subroutine:
bid = 1 !$OMP PARALLEL DEFAULT(SHARED) !$omp do do k=1,km-1 ! km = 60 call ParallelAtkmLoop_sub(bid, k) end do !$omp end do !$OMP END PARALLEL endtime = omp_get_wtime() ... subroutine ParallelAtkmLoop_sub(bid, k) ... do kk=1,2 do j=1,ny_block ! ny_block = 100 do i=1,nx_block ! nx_block = 81 ... enddo enddo enddo end subroutine ParallelAtkmLoop_sub The first stage of optimization includes two changes.
- Moving the parallelization two cycles higher, to the level of the do k loop. Due to this, the number of occurrences in the parallel region decreased by 120 times.
- The application used the LOGICAL array as a mask to select a code. I redid the code used to form the values to get rid of unnecessary manipulations with the mask array.
As a result of these two changes, the performance increased by 2.46 times compared with the initial attempt to parallelize. This is a good result, but is it worth staying there?
In the innermost loop, we see the following:
... {construct masks} if ( LMASK1(i,j) ) then ... {code} endif if ( LMASK2(i,j) ) then ... {code} endif if( LMASK3(i,j) ) then ... {code} endif It turns out that each iteration has a different amount of work. In this case, it is better to use dynamic planning. The next stage of optimization is applied to ParallelAtkmLoopDynamic . This is the same code as ParallelAtkmLoop , but with the addition of schedule (dynamic) to ! $ Omp do .
This simple change alone resulted in a speed increase of 1.25 times. Note that dynamic scheduling is not the only possible planning method. There are other types worth exploring. Also remember that for this type of planning a modifier (fragment size) is often added.
The next level of optimization, which provides an acceleration of 1.52 times, can be called aggressive optimization. To achieve this incremental speed increase of 52%, tangible programming efforts are required (however, nothing prohibitively complex). The possibility of this optimization is determined by analyzing the assembler code in VTune.
It should be emphasized that there is no need to understand assembly code for its analysis. As a rule, one can proceed from the following:
the more assembler code, the lower the performance.
You can draw a direct parallel: the harder (more complex) the assembler code, the more likely that the compiler will miss the optimization possibilities. If you see missing opportunities, you can use a simple technique to help the compiler optimize the code.
In the code of the main algorithm we see.
Code
subroutine ParallelAtkmLoopDynamic_sub(bid, k) use omp_lib use mod_globals implicit none !----------------------------------------------------------------------- ! ! dummy variables ! !----------------------------------------------------------------------- integer :: bid,k !----------------------------------------------------------------------- ! ! local variables ! !----------------------------------------------------------------------- real , dimension(nx_block,ny_block,2) :: & WORK1, WORK2, WORK3, WORK4 ! work arrays real , dimension(nx_block,ny_block) :: & WORK2_NEXT, WORK4_NEXT ! WORK2 or WORK4 at next level logical , dimension(nx_block,ny_block) :: & LMASK1, LMASK2, LMASK3 ! flags integer :: kk, j, i ! loop indices !----------------------------------------------------------------------- ! ! code ! !----------------------------------------------------------------------- do kk=1,2 do j=1,ny_block do i=1,nx_block if(TLT%K_LEVEL(i,j,bid) == k) then if(TLT%K_LEVEL(i,j,bid) < KMT(i,j,bid)) then LMASK1(i,j) = TLT%ZTW(i,j,bid) == 1 LMASK2(i,j) = TLT%ZTW(i,j,bid) == 2 if(LMASK2(i,j)) then LMASK3(i,j) = TLT%K_LEVEL(i,j,bid) + 1 < KMT(i,j,bid) else LMASK3(i,j) = .false. endif else LMASK1(i,j) = .false. LMASK2(i,j) = .false. LMASK3(i,j) = .false. endif else LMASK1(i,j) = .false. LMASK2(i,j) = .false. LMASK3(i,j) = .false. endif if ( LMASK1(i,j) ) then WORK1(i,j,kk) = KAPPA_THIC(i,j,kbt,k,bid) & * SLX(i,j,kk,kbt,k,bid) * dz(k) WORK2(i,j,kk) = c2 * dzwr(k) * ( WORK1(i,j,kk) & - KAPPA_THIC(i,j,ktp,k+1,bid) * SLX(i,j,kk,ktp,k+1,bid) & * dz(k+1) ) WORK2_NEXT(i,j) = c2 * ( & KAPPA_THIC(i,j,ktp,k+1,bid) * SLX(i,j,kk,ktp,k+1,bid) - & KAPPA_THIC(i,j,kbt,k+1,bid) * SLX(i,j,kk,kbt,k+1,bid) ) WORK3(i,j,kk) = KAPPA_THIC(i,j,kbt,k,bid) & * SLY(i,j,kk,kbt,k,bid) * dz(k) WORK4(i,j,kk) = c2 * dzwr(k) * ( WORK3(i,j,kk) & - KAPPA_THIC(i,j,ktp,k+1,bid) * SLY(i,j,kk,ktp,k+1,bid) & * dz(k+1) ) WORK4_NEXT(i,j) = c2 * ( & KAPPA_THIC(i,j,ktp,k+1,bid) * SLY(i,j,kk,ktp,k+1,bid) - & KAPPA_THIC(i,j,kbt,k+1,bid) * SLY(i,j,kk,kbt,k+1,bid) ) if( abs( WORK2_NEXT(i,j) ) < abs( WORK2(i,j,kk) ) ) then WORK2(i,j,kk) = WORK2_NEXT(i,j) endif if ( abs( WORK4_NEXT(i,j) ) < abs( WORK4(i,j,kk ) ) ) then WORK4(i,j,kk) = WORK4_NEXT(i,j) endif endif if ( LMASK2(i,j) ) then WORK1(i,j,kk) = KAPPA_THIC(i,j,ktp,k+1,bid) & * SLX(i,j,kk,ktp,k+1,bid) WORK2(i,j,kk) = c2 * ( WORK1(i,j,kk) & - ( KAPPA_THIC(i,j,kbt,k+1,bid) & * SLX(i,j,kk,kbt,k+1,bid) ) ) WORK1(i,j,kk) = WORK1(i,j,kk) * dz(k+1) WORK3(i,j,kk) = KAPPA_THIC(i,j,ktp,k+1,bid) & * SLY(i,j,kk,ktp,k+1,bid) WORK4(i,j,kk) = c2 * ( WORK3(i,j,kk) & - ( KAPPA_THIC(i,j,kbt,k+1,bid) & * SLY(i,j,kk,kbt,k+1,bid) ) ) WORK3(i,j,kk) = WORK3(i,j,kk) * dz(k+1) endif if( LMASK3(i,j) ) then if (k.lt.km-1) then ! added to avoid out of bounds access WORK2_NEXT(i,j) = c2 * dzwr(k+1) * ( & KAPPA_THIC(i,j,kbt,k+1,bid) * SLX(i,j,kk,kbt,k+1,bid) * dz(k+1) - & KAPPA_THIC(i,j,ktp,k+2,bid) * SLX(i,j,kk,ktp,k+2,bid) * dz(k+2)) WORK4_NEXT(i,j) = c2 * dzwr(k+1) * ( & KAPPA_THIC(i,j,kbt,k+1,bid) * SLY(i,j,kk,kbt,k+1,bid) * dz(k+1) - & KAPPA_THIC(i,j,ktp,k+2,bid) * SLY(i,j,kk,ktp,k+2,bid) * dz(k+2)) end if if( abs( WORK2_NEXT(i,j) ) < abs( WORK2(i,j,kk) ) ) & WORK2(i,j,kk) = WORK2_NEXT(i,j) if( abs(WORK4_NEXT(i,j)) < abs(WORK4(i,j,kk)) ) & WORK4(i,j,kk) = WORK4_NEXT(i,j) endif enddo enddo enddo end subroutine Version2_ParallelAtkmLoop_sub Let's start Intel Amplifier (VTune) and as an example we will consider line 540.

This is part of the instruction that multiplies two numbers. For this partial information you can expect:
- load value for any SLX index;
- multiplication by the value of any index dz.
If you click the Assembly button in the Amplifier.

Then we sort by line number of the code.

In line of code 540 we see the following.

A total of 46 assembly instructions are used to multiply two numbers.
We now turn to mutual influence.
These two numbers are cells of two arrays. The SLX array has six subscriptions, the other array has one. The last two assembler instructions: vmovss from memory and vmulss from memory. We hoped to get a fully optimized code that met our expectations. In the above code, 44 out of 46 assembler functions are associated with the calculation of array indices for these two variables. Naturally, several instructions may be required to obtain indices in arrays, but 44 is clearly too many. Is it possible to reduce the complexity in any way?
When viewing the source code (the latest version shown above), you can see that the last two subordinate SLX scripts and one subordinate dz script are invariant for the two most internal loops. In the case of SLX, the left of two indices (two variables controlling the most internal loops) is a continuous array fragment. The compiler did not recognize the constant (right) array indices as candidates for an invariant loop code that can be inferred from the loop. In addition, the compiler could not recognize the two indices, located to the left of all, to collapse into one index.
This is a good example of possible optimization that can be implemented by the compiler. In this case, the following optimization procedure, in which invariant subordinate scenarios are derived from the cycle, provides an increase in productivity by 1.52 times.
We now know that much of the do code includes contiguous array fragments with several subordinate scripts. Is it possible to reduce the number of subordinate scenarios without rewriting the entire application?
Answer: yes, it is possible if you encapsulate smaller sections of arrays represented by a smaller number of subordinate scripts. How to do this in our code example?
I decided to apply this approach to two levels of nesting.
- At the outermost level of bid (module data indicates that 65 bid values are used in the actual code).
- At the next level - at the level of the do k cycle. In addition, we combine the first two indices into one.
The outermost layer transmits fragments of the bid level array.
bid = 1 ! in real application bid may iterate ! peel off the bid call ParallelNestedRank1_bid( & TLT%K_LEVEL(:,:,bid), & KMT(:,:,bid), & TLT%ZTW(:,:,bid), & KAPPA_THIC(:,:,:,:,bid), & SLX(:,:,:,:,:,bid), & SLY(:,:,:,:,:,bid)) … subroutine ParallelNestedRank1_bid(K_LEVEL_bid, KMT_bid, ZTW_bid, KAPPA_THIC_bid, SLX_bid, SLY_bid) use omp_lib use mod_globals implicit none integer, dimension(nx_block , ny_block) :: K_LEVEL_bid, KMT_bid, ZTW_bid real, dimension(nx_block,ny_block,2,km) :: KAPPA_THIC_bid real, dimension(nx_block,ny_block,2,2,km) :: SLX_bid, SLY_bid … Note that for arrays without pointers (distributed or with fixed sizes) arrays are continuous. This makes it possible to “cut off” the rightmost indices for transmitting a fragment of a continuous array, for which you simply need to calculate the offset in a subset of a larger array. At the same time, in order to try to “cut off” any other indices, except the rightmost ones, you need to create a temporary array, which should be avoided. However, in some cases, even this may be appropriate.
At the second nested level, we have expanded the additional index of the array of the do k loop, and also compressed the first two indices into one.
!$OMP PARALLEL DEFAULT(SHARED) !$omp do do k=1,km-1 call ParallelNestedRank1_bid_k( & K_LEVEL_bid, KMT_bid, ZTW_bid, & KAPPA_THIC_bid(:,:,:,k), & KAPPA_THIC_bid(:,:,:,k+1), KAPPA_THIC_bid(:,:,:,k+2),& SLX_bid(:,:,:,:,k), SLY_bid(:,:,:,:,k), & SLX_bid(:,:,:,:,k+1), SLY_bid(:,:,:,:,k+1), & SLX_bid(:,:,:,:,k+2), SLY_bid(:,:,:,:,k+2), & dz(k),dz(k+1),dz(k+2),dzwr(k),dzwr(k+1)) end do !$omp end do !$OMP END PARALLEL end subroutine ParallelNestedRank1_bid subroutine ParallelNestedRank11_bid_k( & k, K_LEVEL_bid, KMT_bid, ZTW_bid, & KAPPA_THIC_bid_k, KAPPA_THIC_bid_kp1, KAPPA_THIC_bid_kp2, & SLX_bid_k, SLY_bid_k, & SLX_bid_kp1, SLY_bid_kp1, & SLX_bid_kp2, SLY_bid_kp2, & dz_k,dz_kp1,dz_kp2,dzwr_k,dzwr_kp1) use mod_globals implicit none !----------------------------------------------------------------------- ! ! dummy variables ! !----------------------------------------------------------------------- integer :: k integer, dimension(nx_block*ny_block) :: K_LEVEL_bid, KMT_bid, ZTW_bid real, dimension(nx_block*ny_block,2) :: KAPPA_THIC_bid_k, KAPPA_THIC_bid_kp1 real, dimension(nx_block*ny_block,2) :: KAPPA_THIC_bid_kp2 real, dimension(nx_block*ny_block,2,2) :: SLX_bid_k, SLY_bid_k real, dimension(nx_block*ny_block,2,2) :: SLX_bid_kp1, SLY_bid_kp1 real, dimension(nx_block*ny_block,2,2) :: SLX_bid_kp2, SLY_bid_kp2 real :: dz_k,dz_kp1,dz_kp2,dzwr_k,dzwr_kp1 ... ! next note index (i,j) compression to (ij) do kk=1,2 do ij=1,ny_block*nx_block if ( LMASK1(ij) ) then Notice that a fragment of a continuous array is transmitted at the call point (link). Empty arguments to the procedure being called indicate a continuous chunk of memory of the same size with a different set of indices. If you are careful when working in FORTRAN, it is quite feasible.
All actions to create code are reduced to copy and paste operations, and then to search and replace. Except for this, the code flow does not change. This could be done by an attentive novice programmer who has the necessary instructions.
In future versions of the compiler, built-in optimization tools may make all these actions unnecessary, but now “unnecessary” programming can in some cases lead to a significant increase in performance (in this case by 52%).
Equivalent instruction is now such.

The assembler code now looks like this.

Instead of 46 instructions, 6 is left, that is, 7.66 times less. Thus, reducing the number of subordinate scripts in the array allows you to reduce the number of instructions.
The introduction of a two-level investment with "cutting" led to an increase in productivity by 1.52 times. Is 52% more productivity worth the extra effort? Decide for yourself, everything is subjective here. It can be assumed that optimization algorithms incorporated in future versions of compilers will themselves extract subordinate scripts of invariant arrays, which was done manually above. But for now you can use the described method of "cutting" and compressing indexes.
I hope my recommendations will be helpful.
» Sample source code
Source: https://habr.com/ru/post/301428/
All Articles