Yandex.Algorithm. Analysis of last year's qualifying round and the last chance to participate in the championship
As you know, the next ACM ICPC championship ended yesterday. Congratulations to students of MIPT, ITMO, UrFU and UNN with excellent performance, the guys from St. Petersburg State University - with the 1st place. Now we invite everyone to take part in Yandex. Algorithm 2016. This year the championship final will be held in Minsk.
This year, for the first time in addition to traditional prizes, the winners will have the opportunity to get an internship at Yandex. On May 22, registration will be closed and you will only have to follow the other participants in the qualifying rounds. The qualifying round will last two days this year - from 21 to 22 May. Rounds will again be evaluated on the system TCM / Time . For those who are interested in the complexity of the task they are waiting for, we made out a tour of last year’s qualification. You also have the opportunity to practice on it.
')
UPDATE: The qualifying round of Yandex.Algorithm 2016 has already begun, come and solve the tasks that we will definitely analyze in the future. In our opinion, the tasks are no worse than last year.
Michael is a regular Internet user. When Mikhail searches for something on the Internet using Yandex, it happens that he allows typos in the search query. Of course, in most cases, Yandex can guess what Michael meant and correct the request. For example, if Mikhail is sealed and writes “deoxyribonucleic” (which is not surprising), Yandex will correct the request for “deoxyribonucleic” .
Perhaps you thought that in this task you need to write a program that corrects typos in the user's request. This is not so: apart from this task, you are offered 5 more fascinating tasks, and there is not much time left until the end of the competition. Just check if the next Michael request contains typos.
Input data
The first line of the input file contains Michael's query: from 1 to 5 words, consisting of lowercase Latin letters and separated by single spaces. The second line contains an integer N (1 ≤ N ≤ 100) : the number of words contained in the Yandex dictionary (do not worry, in reality, the number of words contained in Yandex dictionaries is much more than one hundred). The third line contains words from the dictionary. Each word is a string consisting of lowercase Latin letters. Words are separated by single spaces. It is guaranteed that the words from the query and the words from the dictionary contain no more than 20 letters.
Output
In the only line of the output file output “Correct” (without quotes), if all the words from Michael's query are contained in the existing dictionary, and “Misspell” (without quotes), if at least one word is not in the dictionary.
The solution of the problem
In the task, it was necessary to determine whether all the words from the first set belong to the second set.
With the restrictions in this problem, a simple solution of the trivial in O (N · M) would suffice, where N and M are the sizes of the first and second sets, respectively. To implement it, you need to directly verify that every word from the first set is in the second.
A fairly simple implementation is obtained in python:
Anna is a regular internet user. Anna loves listening to music and using the Yandex.Music service. One day, while listening to songs on Yandex.Music in the random-mix mode, Anna was very upset that after her favorite band "Epidemia", Grigory Leps suddenly began to play. Burning with indignation, Anna wrote an angry letter to the technical support service, after which the Yandex.Music development team decided to improve the selection of the next song to play.
In total, the service has N songs, each of which Anna wants to listen to at least once. At the same time, Anna does not object to re-listening to songs, but very much objects to an abrupt change of genres. In addition to the music itself, the Yandex.Music database contains information about how some songs resemble each other in genre. Each record has the form (a, b, U) and means that if you turn on song number b immediately after song number a , the user will experience U units of discontent.
It is known that all users, including Anna, pay attention to the most unsuccessful switchings of songs, therefore by discontent from listening to some playlist we will call the maximum for all dissatisfactions from switching in a row of going songs.
Having such data, Yandex.Music should make an optimal playlist for the user that meets the following conditions:
Can you create a playlist that meets the specified conditions?
Input data
The first line of the input file contains two integers N and M (1 ≤ N ≤ 100 000, 1 ≤ M ≤ 200 000) , separated by spaces: the number of songs Anna wants to listen to and the number of records of transitions between these songs, respectively. The next M lines contain three integers each ai , bi , Ui (1 ≤ ai, bi ≤ N, ai bi, 1 ≤ Ui ≤ 1 000 000 000) separated by spaces, which means that if you turn on the song with the number bi immediately after the song with the number ai , the user will experience Ui units of discontent. It is guaranteed that no transition from one song to another is found twice in the recordings.
Output
Output a single number: the maximum dissatisfaction Anna will experience in the process of listening to the optimally compiled playlist, or -1 if it is impossible to compile a playlist.
The solution of the problem
Let's learn how to solve a problem without the additional parameter Ui .
Given a directed graph with N vertices and M arcs, it is required to determine whether it is possible to construct such a sequence of graph vertices that any two adjacent vertices are connected by an arc, and all N different graph vertices are included in this sequence.
Note that the strongly connected component of this graph can be replaced by one vertex. This can be done because for any strongly connected graph, one can construct a sequence of vertices in which all vertices of the graph will occur at least once. Let us prove this statement. Suppose we have some sequence with K different vertices, ending with a vertex x . Choose any of the vertices y not yet represented in it, since if the graph is strongly connected, then there exists a chain of arcs leading from x to y , we add vertices through which this chain passes into the sequence. In the new sequence obtained, at least K + 1 different vertices.
After we have compressed the strongly connected components of the graph to new vertices, the oriented graph will remain without cycles. It is easy to see that in order to be able to build the original sequence of vertices, this graph should have the only way to order the vertices topologically, and between any two adjacent vertices in the topological contract there should be an arc.
Additionally, we note that if for some graph it is possible to build the required sequence of vertices, then after adding additional arcs to it, this property will remain.
We will look for the answer to the problem with a binary search for the maximum dissatisfaction that Anna will experience in the process of listening to the optimally composed playlist.
So, we get the following algorithm for solving the problem:
By binary search, we choose the value U , for which we leave only arcs with Ui ≤ U in the graph.
We drag the strongly connected components of the obtained graph into separate vertices.
In the resulting graph we find the topological order of the vertices, check that between all pairs of neighboring vertices there is an arc.
Depending on whether or not it was possible to find the required sequence for a given value of U , we determine in which direction the binary search should move.
Useful links:
en.wikipedia.org/wiki/Strongly_connected_component
en.wikipedia.org/wiki/Topological_sorting
Ivan is a regular Internet user. One of Ivan's favorite games is “Hat”, in which you need to quickly explain the hidden word. In order to play it was interesting, he searches for unusual words on the Internet, asking various search queries.
Ivana always wondered why one document was higher than the other in search results. By asking about this in the Yandex search, Ivan found out that the documents are sorted automatically in descending order of documents. And relevance, in turn, is calculated by the formula selected by a special algorithm.
In this problem we will use a simplified version of the relevance formula - a linear combination of document parameters. The ranking formula is defined by N parameters (a1, a2, ..., aN) , and each document is described by N numerical parameters (f1, f2, ..., fN) .
Relevance is determined by the formula:
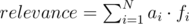
The Internet is changing very quickly, and some documents can change several times a minute. Of course, after this you need to change some of the parameters of this document.
Can you find the most relevant in the context of changing document parameters?
Input data
The first line of the input data contains a single integer N (1 ≤ N ≤ 100) - the number of parameters in the ranking formula. The second line contains N integers ai (0 ≤ ai ≤ 100 000 000).
The third line of the input data contains a single integer D (10 ≤ D ≤ 100 000, N · D ≤ 100 000) - the number of documents for ranking. Further, in the D lines there are written N integers fij (0 ≤ fij ≤ 100 000 000) - the numerical parameters of the i -th document.
The next line contains a single integer Q (1 ≤ Q ≤ 100 000) - the number of queries to the ranking system. The following Q lines describe the queries. The request for issuing the most relevant documents is specified by a pair of 1 K (1 ≤ K ≤ 10) . A request to change a document parameter is given by a quadruple 2 djv (1 ≤ d ≤ D, 1 ≤ j ≤ N, 0 ≤ v ≤ 100 000 000) and means that the j -th parameter of the d -th document becomes equal to v .
Output
After each query of the first type, output in one line the ordinal numbers K of the most relevant documents in descending order of relevance (the numbers should be separated by single spaces). It is guaranteed that all documents at any given time have different relevance values.
The solution of the problem
Let's start with the analysis of requests of the second type. Note that when such queries are executed, relevance changes only in one document, and moreover, a new relevance can be calculated as O (1) .
To perform queries of the first type, you need to find K maximal elements in the relevance list. To do this, you can use a balanced search tree.
When implemented in C ++, you can use the standard container std :: map , and when using Java, you can use the TreeMap . When using these containers, you can delete the old values ​​of the relevance of the documents by key, and then add the document with the new value, and look for the maximum values ​​by a partial iterator pass from the maximum key.
Operations of the second type will be processed for)
(deletion and addition by key), and the operations of finding the K max for )
(at least for C ++).
The novel is a regular Internet user. Like many other regular users, Roman is very impatient. For example, now Roman is waiting for news updates on the Yandex main page and is constantly clicking “Refresh” in the browser. In order not to overload Yandex with a huge number of requests (Roman is very impatient!), All Roman requests are added to the queue, from where they are sent to the news service so that requests are no more frequent than some frequency specified in the configuration.
The frequency limit can be defined in two ways: no more than X requests per second, or 1 request no more than Y seconds. Each Roman request will be processed at that moment in time when its processing does not lead to a violation of the frequency limit, but, naturally, not before the moment the request was sent. For more explanation, see examples.
Can you write a program that simulates the work of the service to limit the frequency of requests and reports at what time each request is processed?
Input data
The first line contains a frequency limit in the format X / Y , where X and Y are two integers (1 ≤ X, Y ≤ 10 000) , at least one of which is 1 . If Y = 1 , then the service should not process more than X requests per second. If X = 1 , then the service should not process more than one request in Y seconds.
The second line contains the number N (1 ≤ N ≤ 100 000) - the number of page refresh requests that Roman sent to the server by clicking the Refresh button in the browser.
The next line contains N integers ti (1 ≤ ti ≤ 1 000 000 000 000 000 000) separated by spaces - the request sending times specified in nanoseconds (1 000 000 000 nanoseconds in one second). It is guaranteed that the numbers ti are arranged in non-decreasing order.
Output
Print N numbers separated by spaces - the processing time of each request. See examples for clarification.
The solution of the problem
To solve the problem, it is enough to read in turn the times of all requests and write to the array the times when they were processed. In order to get the processing time of the i- th request, it suffices to take the minimum of its arrival time and the processing time of the (i-X) -th request increased by Y · 1,000,000,000 (if i ≤ X , the request will be processed immediately upon receipt).
Alexey is a regular Internet user. Once, while using the Yandex.Maps service, Alexey thought: after all, the final image on the screen is probably formed from several smaller rectangular images received from the server. It became interesting to Alexey: how many possible sizes of images there are such that one can make a picture visible on the screen from them.
The visible area of ​​the map is N × M pixels on Alexey’s screen. He is interested in the number of pairs (A, B) (1 ≤ A ≤ N, 1 ≤ B ≤ M) such that the rectangles A × B can be used to lay out the rectangle N × M , placing them close to each other, without overlaps and turns. At the same time, Alexey is sure that sending large images from the server is very expensive, and therefore he is not interested in couples (A, B) , for which A · B> R. Alexey also understands that sending a large number of small pictures is also unprofitable, therefore he is not interested in couples (A, B) , for which A · B <L .
Help Alexey answer his question.
Input data
The only line of the input file contains four integers N, M, L, R (1 ≤ N, M ≤ 1 000 000 000, 1 ≤ L ≤ R ≤ N · M), separated by spaces.
Output
Print a single number: the number of possible pairs that meet the requirements of Alexey.
The solution of the problem
From the condition that the rectangles A Ă— B can be laid out the rectangle N Ă— M, it follows that N is divided by A , and M is divided by B. We form a list of Dn consisting of divisors of N , and a list of Dm of divisors of M. As you know, you can find all the divisors of any number X for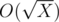
. Having two such lists, you can iterate through all candidate pairs (A, B) by two nested loops and check that the condition L ≤ A · B ≤ R is met. If the condition is satisfied, the answer must be increased by 1.
Bonus: the greatest number of divisors of a number up to 1 000 000 000 - 1344.
Yura is a regular Internet user. He loves to read the history of the cities of the world, and even more he loves to travel and during these travels to tell friends about what happened in one place or another in the 10th or 16th century. When Yura comes to a new city, he already has a list of attractions in this area, and all that remains is to get the route to these places correctly.
In order to make a good route, Yura uses the Yandex.Maps service. One day, he noticed a button with a traffic light and pressed it. Roads on the map were painted in different colors. Yura became interested in how Yandex determines traffic congestion, and decided to search for information on the Internet.
In this task, we use a simplified version of the definition of road congestion. All roads in the map service are numbered with integers from 1 to M. Two numbers Li and Ri are known about each road. If at the current moment in time there are less than Li cars on the road, then the road is considered free, and on the map it is drawn in green. If at the current time point there are more than Ri cars on the road, then the road is considered to be loaded, and on the map it is drawn in red. If the road is neither free nor loaded, then it is drawn on the service in orange.
You are given a description of the roads from the map service and information about where N cars are located. Can you determine what color these roads should be drawn on the map?
Input data
The first input line contains an integer M (1 ≤ M ≤ 1 000) - the number of roads. Then follow M lines with two integers Li and Ri (1 ≤ Li ≤ Ri ≤ 10) in each - parameters of the i- th road. The next line contains one integer N (1 ≤ N ≤ 1 000) - the number of cars currently on the roads. The next line contains N integers rj (1 ≤ rj ≤ M) - the numbers of the roads where the cars are located.
Output
Output M lines, one for each road from the input data. If the i- th road should be drawn in red, then output “Red” in the i- th line, if the orange is “Orange”, otherwise print “Green”.
The solution of the problem
To begin with, in the task it is necessary to count the number of cars on it for each road. And then for each road by its parameters it is easy to determine the degree of its workload.
Also, a fairly simple implementation is obtained in python:
This year, for the first time in addition to traditional prizes, the winners will have the opportunity to get an internship at Yandex. On May 22, registration will be closed and you will only have to follow the other participants in the qualifying rounds. The qualifying round will last two days this year - from 21 to 22 May. Rounds will again be evaluated on the system TCM / Time . For those who are interested in the complexity of the task they are waiting for, we made out a tour of last year’s qualification. You also have the opportunity to practice on it.
')
UPDATE: The qualifying round of Yandex.Algorithm 2016 has already begun, come and solve the tasks that we will definitely analyze in the future. In our opinion, the tasks are no worse than last year.
A. Typos
Michael is a regular Internet user. When Mikhail searches for something on the Internet using Yandex, it happens that he allows typos in the search query. Of course, in most cases, Yandex can guess what Michael meant and correct the request. For example, if Mikhail is sealed and writes “deoxyribonucleic” (which is not surprising), Yandex will correct the request for “deoxyribonucleic” .
Perhaps you thought that in this task you need to write a program that corrects typos in the user's request. This is not so: apart from this task, you are offered 5 more fascinating tasks, and there is not much time left until the end of the competition. Just check if the next Michael request contains typos.
Input data
The first line of the input file contains Michael's query: from 1 to 5 words, consisting of lowercase Latin letters and separated by single spaces. The second line contains an integer N (1 ≤ N ≤ 100) : the number of words contained in the Yandex dictionary (do not worry, in reality, the number of words contained in Yandex dictionaries is much more than one hundred). The third line contains words from the dictionary. Each word is a string consisting of lowercase Latin letters. Words are separated by single spaces. It is guaranteed that the words from the query and the words from the dictionary contain no more than 20 letters.
Output
In the only line of the output file output “Correct” (without quotes), if all the words from Michael's query are contained in the existing dictionary, and “Misspell” (without quotes), if at least one word is not in the dictionary.
The solution of the problem
In the task, it was necessary to determine whether all the words from the first set belong to the second set.
With the restrictions in this problem, a simple solution of the trivial in O (N · M) would suffice, where N and M are the sizes of the first and second sets, respectively. To implement it, you need to directly verify that every word from the first set is in the second.
A fairly simple implementation is obtained in python:
import sys words = sys.stdin.readline().split() _ = sys.stdin.readline() d = sys.stdin.readline().split() print "Correct" if all(word in d for word in words) else "Misspell" B. Optimal playlist
Anna is a regular internet user. Anna loves listening to music and using the Yandex.Music service. One day, while listening to songs on Yandex.Music in the random-mix mode, Anna was very upset that after her favorite band "Epidemia", Grigory Leps suddenly began to play. Burning with indignation, Anna wrote an angry letter to the technical support service, after which the Yandex.Music development team decided to improve the selection of the next song to play.
In total, the service has N songs, each of which Anna wants to listen to at least once. At the same time, Anna does not object to re-listening to songs, but very much objects to an abrupt change of genres. In addition to the music itself, the Yandex.Music database contains information about how some songs resemble each other in genre. Each record has the form (a, b, U) and means that if you turn on song number b immediately after song number a , the user will experience U units of discontent.
It is known that all users, including Anna, pay attention to the most unsuccessful switchings of songs, therefore by discontent from listening to some playlist we will call the maximum for all dissatisfactions from switching in a row of going songs.
Having such data, Yandex.Music should make an optimal playlist for the user that meets the following conditions:
- Each song is contained in it at least once;
- For each pair of adjacent songs there is a corresponding record in the database (it is better not to switch the songs, not knowing how this can turn out);
- The discontent from listening to the playlist should be as small as possible.
Can you create a playlist that meets the specified conditions?
Input data
The first line of the input file contains two integers N and M (1 ≤ N ≤ 100 000, 1 ≤ M ≤ 200 000) , separated by spaces: the number of songs Anna wants to listen to and the number of records of transitions between these songs, respectively. The next M lines contain three integers each ai , bi , Ui (1 ≤ ai, bi ≤ N, ai bi, 1 ≤ Ui ≤ 1 000 000 000) separated by spaces, which means that if you turn on the song with the number bi immediately after the song with the number ai , the user will experience Ui units of discontent. It is guaranteed that no transition from one song to another is found twice in the recordings.
Output
Output a single number: the maximum dissatisfaction Anna will experience in the process of listening to the optimally compiled playlist, or -1 if it is impossible to compile a playlist.
The solution of the problem
Let's learn how to solve a problem without the additional parameter Ui .
Given a directed graph with N vertices and M arcs, it is required to determine whether it is possible to construct such a sequence of graph vertices that any two adjacent vertices are connected by an arc, and all N different graph vertices are included in this sequence.
Note that the strongly connected component of this graph can be replaced by one vertex. This can be done because for any strongly connected graph, one can construct a sequence of vertices in which all vertices of the graph will occur at least once. Let us prove this statement. Suppose we have some sequence with K different vertices, ending with a vertex x . Choose any of the vertices y not yet represented in it, since if the graph is strongly connected, then there exists a chain of arcs leading from x to y , we add vertices through which this chain passes into the sequence. In the new sequence obtained, at least K + 1 different vertices.
After we have compressed the strongly connected components of the graph to new vertices, the oriented graph will remain without cycles. It is easy to see that in order to be able to build the original sequence of vertices, this graph should have the only way to order the vertices topologically, and between any two adjacent vertices in the topological contract there should be an arc.
Additionally, we note that if for some graph it is possible to build the required sequence of vertices, then after adding additional arcs to it, this property will remain.
We will look for the answer to the problem with a binary search for the maximum dissatisfaction that Anna will experience in the process of listening to the optimally composed playlist.
So, we get the following algorithm for solving the problem:
By binary search, we choose the value U , for which we leave only arcs with Ui ≤ U in the graph.
We drag the strongly connected components of the obtained graph into separate vertices.
In the resulting graph we find the topological order of the vertices, check that between all pairs of neighboring vertices there is an arc.
Depending on whether or not it was possible to find the required sequence for a given value of U , we determine in which direction the binary search should move.
Useful links:
en.wikipedia.org/wiki/Strongly_connected_component
en.wikipedia.org/wiki/Topological_sorting
C. Document ranking
Ivan is a regular Internet user. One of Ivan's favorite games is “Hat”, in which you need to quickly explain the hidden word. In order to play it was interesting, he searches for unusual words on the Internet, asking various search queries.
Ivana always wondered why one document was higher than the other in search results. By asking about this in the Yandex search, Ivan found out that the documents are sorted automatically in descending order of documents. And relevance, in turn, is calculated by the formula selected by a special algorithm.
In this problem we will use a simplified version of the relevance formula - a linear combination of document parameters. The ranking formula is defined by N parameters (a1, a2, ..., aN) , and each document is described by N numerical parameters (f1, f2, ..., fN) .
Relevance is determined by the formula:
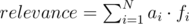
The Internet is changing very quickly, and some documents can change several times a minute. Of course, after this you need to change some of the parameters of this document.
Can you find the most relevant in the context of changing document parameters?
Input data
The first line of the input data contains a single integer N (1 ≤ N ≤ 100) - the number of parameters in the ranking formula. The second line contains N integers ai (0 ≤ ai ≤ 100 000 000).
The third line of the input data contains a single integer D (10 ≤ D ≤ 100 000, N · D ≤ 100 000) - the number of documents for ranking. Further, in the D lines there are written N integers fij (0 ≤ fij ≤ 100 000 000) - the numerical parameters of the i -th document.
The next line contains a single integer Q (1 ≤ Q ≤ 100 000) - the number of queries to the ranking system. The following Q lines describe the queries. The request for issuing the most relevant documents is specified by a pair of 1 K (1 ≤ K ≤ 10) . A request to change a document parameter is given by a quadruple 2 djv (1 ≤ d ≤ D, 1 ≤ j ≤ N, 0 ≤ v ≤ 100 000 000) and means that the j -th parameter of the d -th document becomes equal to v .
Output
After each query of the first type, output in one line the ordinal numbers K of the most relevant documents in descending order of relevance (the numbers should be separated by single spaces). It is guaranteed that all documents at any given time have different relevance values.
The solution of the problem
Let's start with the analysis of requests of the second type. Note that when such queries are executed, relevance changes only in one document, and moreover, a new relevance can be calculated as O (1) .
To perform queries of the first type, you need to find K maximal elements in the relevance list. To do this, you can use a balanced search tree.
When implemented in C ++, you can use the standard container std :: map , and when using Java, you can use the TreeMap . When using these containers, you can delete the old values ​​of the relevance of the documents by key, and then add the document with the new value, and look for the maximum values ​​by a partial iterator pass from the maximum key.
Operations of the second type will be processed for
D. Frequency Limiter
The novel is a regular Internet user. Like many other regular users, Roman is very impatient. For example, now Roman is waiting for news updates on the Yandex main page and is constantly clicking “Refresh” in the browser. In order not to overload Yandex with a huge number of requests (Roman is very impatient!), All Roman requests are added to the queue, from where they are sent to the news service so that requests are no more frequent than some frequency specified in the configuration.
The frequency limit can be defined in two ways: no more than X requests per second, or 1 request no more than Y seconds. Each Roman request will be processed at that moment in time when its processing does not lead to a violation of the frequency limit, but, naturally, not before the moment the request was sent. For more explanation, see examples.
Can you write a program that simulates the work of the service to limit the frequency of requests and reports at what time each request is processed?
Input data
The first line contains a frequency limit in the format X / Y , where X and Y are two integers (1 ≤ X, Y ≤ 10 000) , at least one of which is 1 . If Y = 1 , then the service should not process more than X requests per second. If X = 1 , then the service should not process more than one request in Y seconds.
The second line contains the number N (1 ≤ N ≤ 100 000) - the number of page refresh requests that Roman sent to the server by clicking the Refresh button in the browser.
The next line contains N integers ti (1 ≤ ti ≤ 1 000 000 000 000 000 000) separated by spaces - the request sending times specified in nanoseconds (1 000 000 000 nanoseconds in one second). It is guaranteed that the numbers ti are arranged in non-decreasing order.
Output
Print N numbers separated by spaces - the processing time of each request. See examples for clarification.
The solution of the problem
To solve the problem, it is enough to read in turn the times of all requests and write to the array the times when they were processed. In order to get the processing time of the i- th request, it suffices to take the minimum of its arrival time and the processing time of the (i-X) -th request increased by Y · 1,000,000,000 (if i ≤ X , the request will be processed immediately upon receipt).
E. Size of cards
Alexey is a regular Internet user. Once, while using the Yandex.Maps service, Alexey thought: after all, the final image on the screen is probably formed from several smaller rectangular images received from the server. It became interesting to Alexey: how many possible sizes of images there are such that one can make a picture visible on the screen from them.
The visible area of ​​the map is N × M pixels on Alexey’s screen. He is interested in the number of pairs (A, B) (1 ≤ A ≤ N, 1 ≤ B ≤ M) such that the rectangles A × B can be used to lay out the rectangle N × M , placing them close to each other, without overlaps and turns. At the same time, Alexey is sure that sending large images from the server is very expensive, and therefore he is not interested in couples (A, B) , for which A · B> R. Alexey also understands that sending a large number of small pictures is also unprofitable, therefore he is not interested in couples (A, B) , for which A · B <L .
Help Alexey answer his question.
Input data
The only line of the input file contains four integers N, M, L, R (1 ≤ N, M ≤ 1 000 000 000, 1 ≤ L ≤ R ≤ N · M), separated by spaces.
Output
Print a single number: the number of possible pairs that meet the requirements of Alexey.
The solution of the problem
From the condition that the rectangles A Ă— B can be laid out the rectangle N Ă— M, it follows that N is divided by A , and M is divided by B. We form a list of Dn consisting of divisors of N , and a list of Dm of divisors of M. As you know, you can find all the divisors of any number X for
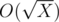. Having two such lists, you can iterate through all candidate pairs (A, B) by two nested loops and check that the condition L ≤ A · B ≤ R is met. If the condition is satisfied, the answer must be increased by 1.Bonus: the greatest number of divisors of a number up to 1 000 000 000 - 1344.
F. Road congestion
Yura is a regular Internet user. He loves to read the history of the cities of the world, and even more he loves to travel and during these travels to tell friends about what happened in one place or another in the 10th or 16th century. When Yura comes to a new city, he already has a list of attractions in this area, and all that remains is to get the route to these places correctly.
In order to make a good route, Yura uses the Yandex.Maps service. One day, he noticed a button with a traffic light and pressed it. Roads on the map were painted in different colors. Yura became interested in how Yandex determines traffic congestion, and decided to search for information on the Internet.
In this task, we use a simplified version of the definition of road congestion. All roads in the map service are numbered with integers from 1 to M. Two numbers Li and Ri are known about each road. If at the current moment in time there are less than Li cars on the road, then the road is considered free, and on the map it is drawn in green. If at the current time point there are more than Ri cars on the road, then the road is considered to be loaded, and on the map it is drawn in red. If the road is neither free nor loaded, then it is drawn on the service in orange.
You are given a description of the roads from the map service and information about where N cars are located. Can you determine what color these roads should be drawn on the map?
Input data
The first input line contains an integer M (1 ≤ M ≤ 1 000) - the number of roads. Then follow M lines with two integers Li and Ri (1 ≤ Li ≤ Ri ≤ 10) in each - parameters of the i- th road. The next line contains one integer N (1 ≤ N ≤ 1 000) - the number of cars currently on the roads. The next line contains N integers rj (1 ≤ rj ≤ M) - the numbers of the roads where the cars are located.
Output
Output M lines, one for each road from the input data. If the i- th road should be drawn in red, then output “Red” in the i- th line, if the orange is “Orange”, otherwise print “Green”.
The solution of the problem
To begin with, in the task it is necessary to count the number of cars on it for each road. And then for each road by its parameters it is easy to determine the degree of its workload.
Also, a fairly simple implementation is obtained in python:
import sys M = int(sys.stdin.readline()) LR = [] C = [0] * M for i in xrange(M): LR.append(map(int, sys.stdin.readline().split())) N = int(sys.stdin.readline()) for r in map(int, sys.stdin.readline().split()): C[r - 1] += 1 for i in xrange(M): print "Green" if C[i] < LR[i][0] else ("Red" if C[i] > LR[i][1] else "Orange") Source: https://habr.com/ru/post/301268/
All Articles