Developing an application to solve Philippine C Crosswords in the Marmalade SDK
Marmalade SDK and Cross Platform
Marmalade SDK as an environment for developing cross-platform mobile (and not only) applications provides the C ++ API to the developer. In fact, this is a set of extensions (Extensions), each of which contains within itself a specific implementation of the functional (work with graphics, file system, network, UI, in-game purchases, work with audio-video, etc.) for each individual platform ( Android, iOS, WinPhone and many other platforms).
Therefore, the developer in the process of writing is practically no need to be tied to the features of a particular platform, except for some cases (perhaps the list is incomplete)
- some functionality may not be supported in a particular OS;
- the developer himself decided to implement the application logic in different ways depending on the OS.
But in the event that a developer needs functionality that is missing from the standard Marmalade SDK distribution kit, he may need to build his Extension himself with his implementation for each platform, and therefore write platform-specific code.
')
Personally, for the implementation of this application, I had enough of a standard set of extensions, so I do not have platform-specific code. Most of the testing and debugging (about 90%) was done on the Windows simulator (the remaining 10% is debugging scaling on the device, since this requires zoom gestures with two fingers). Android and iOS builds are also built on Windows (to do this, you need to install the appropriate tools described in the marmalade dock). Mac is needed only for uploading ipa-file to iTunesConnect console via Apple ApplicationLoader.
A few words about what is the Philippine crossword
Philippine Crossword is a kind of graphic puzzle, in which a picture is encrypted using a set of pairs of numbers. All crosswords should have the only solution. It is necessary to choose and connect pairs of identical numbers with lines so that the result satisfies the following conditions (to which I will repeatedly refer to in the further presentation of the article):
- the length of each line must correspond to the numbers located at its ends;
- lines should not intersect with each other and pass through the same cells;
- lines can go in the vertical and horizontal directions, can be refracted, but can not pass diagonally.
Since the unit has no pair, it is shaded by default. As a result of solving a crossword puzzle, when all pairs of numbers (except for units) are connected by lines, a certain pattern is obtained. Familiarizing yourself with the gif below will shed light on the process of solving the Philippine crossword puzzle:
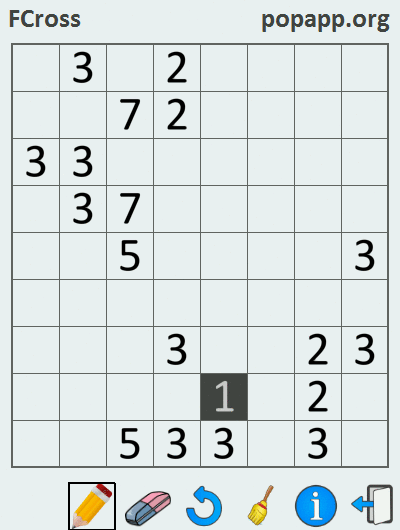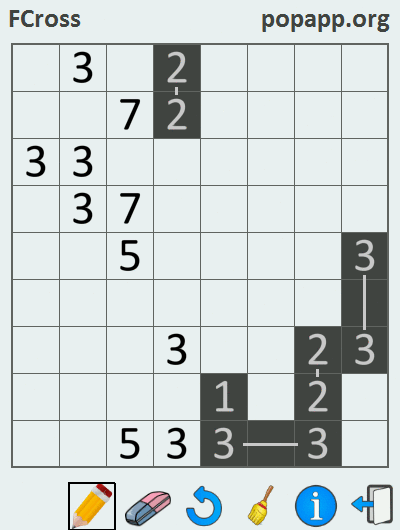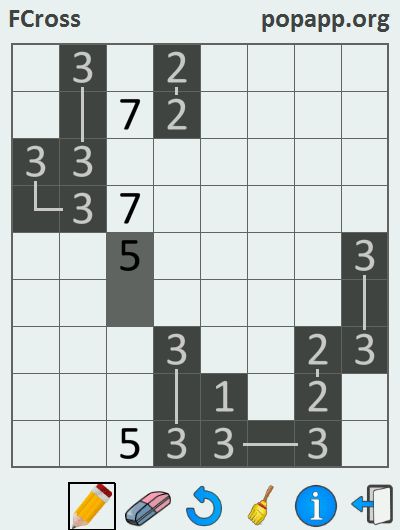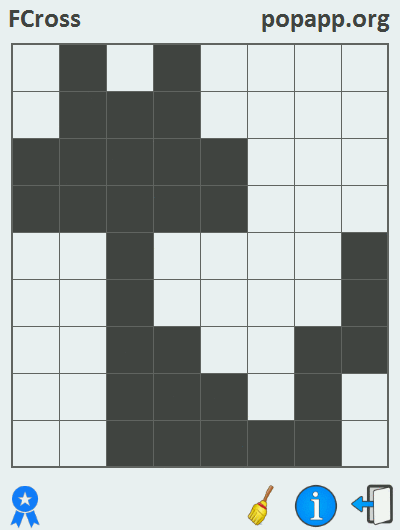
This problem was solved in the Marmalade SDK environment using the C ++ programming language, as a result of which versions of the application for iOS and Android were assembled.
Presentation of the state of the crossword puzzle in RAM
The crossword puzzle grid consists of cells, each of which can be painted over or not painted over (at a different point in time), as well as having or not having a number in it (this property of the cell does not change).
The minimum number used in my crossword puzzles is 1, the maximum is 9. Depending on how the line passes through the cell, it can be painted in several ways (i.e., have several different states).
We list them:
- 1 - the cell is not painted over, i.e. the line does not pass through it;
- 2 - the cell is painted over, but the line does not pass through it either. All cells with the number 1 are in this state.
- 3 - the line passes through the cell vertically;
- 4 - the line passes horizontally through the cell;
- 5 - the line passes through the top and left side of the square of the cell;
- 6 - the line passes through the lower and left side of the square of the cell;
- 7 - the line passes through the top and right side of the square of the cell;
- 8 - the line passes through the bottom and right side of the square of the cell;
- 9 - the cell is an extreme cell line and the line passes through the left side of the square of the cell;
- 10 - the cell is the extreme cell line and the line passes through the right side of the square of the cell;
- 11 - the cell is the extreme cell line and the line passes through the upper side of the square of the cell;
- 12 - the cell is the extreme cell line and the line passes through the bottom side of the square of the cell.
Examples of such states are shown in the figure below.
As a result of solving a crossword puzzle, the user receives the following image:


As a result of solving a crossword puzzle, the user receives the following image:

The first thing that comes to mind as a way to represent the state of a crossword puzzle is a two-dimensional array, that is, a matrix of char elements. The type char has a dimension of 1 byte, that is, it allows you to store one of 2 ^ 8 = 256 states.
We divide the 8-bit byte into two groups: the low and high bits. We get 4 bits in each group, each group makes it possible to store 2 ^ 4 = 16 states.

Thus, we allocate 4 high-order bits for storing information about the method of filling the cell, and 4 low-order bits for storing information about the number indicated in the cell.
#define BYTE_NUMBER_PART 15 // 00001111 #define BYTE_FLAG_PART 240 // 11110000 Description of the structure of the crossword
struct JCStruct { bool Resolved; // char FileName[255]; // char W; // char H; // char M[MAX_PUZZLE_HW][MAX_PUZZLE_ HW]; // char Vector[CHANGE_VECTOR_SIZE][3]; // [i, j, old_value] int Vector_s; // vector start pointer ( ) int Vector_e; // vector end pointer ( ) int DigitsCnt; // - ( ) }; We declare functions that allow using the bitwise multiplication to get the value of the highest (fill flag) and low (number in a cell) group of bits.
char GetNumberFromByte(char c) // , . , 0 { return c & BYTE_NUMBER_PART; } char GetFlagFromByte (char c) // . 0, { return c & BYTE_FLAG_PART; } We encode the possible flags for painting the cells of the crossword puzzle:
#define LN_ONE 16 // 00010000 , / . 1 #define LN_VERTICAL 32 // 00100000 / ; #define LN_HORIZONTAL 48 // 00110000 / ; #define LN_LEFT_TOP 64 // 01000000 / ; #define LN_LEFT_BOTTOM 80 // 01010000 / ; #define LN_RIGHT_TOP 96 // 01100000 / ; #define LN_RIGHT_BOTTOM 112 // 01110000 / ; #define LN_RIGHT 128 // 10000000 / ; #define LN_LEFT 144 // 10010000 / ; #define LN_TOP 160 // 10100000 / ; #define LN_BOTTOM 176 // 10110000 / . Usage example
JCStruct* jc; ... if (GetFlagFromByte(jc->M[i][j]) == LN_HORIZONTAL) // { } Further, all the functionality for drawing and changing the crossword puzzle is implemented using the above constants and functions.
The scenario of connecting two numbers with lines
The user taps his finger on any cell with a number and leads from it to another cell with the same number. When you press a finger, if the line complies with the three rules described at the beginning of the article, the line is fixed, resulting in a fixation of the state of the cells of the matrix through which it passes.
The current line, which the user leads with a finger, is reflected in the CurrentLineStackStruct structure:
struct PointStruct { int x; // int y; // }; struct CurrentLineStackStruct // , { char num; // , PointStruct stack[9]; // , , char len; // }; CurrentLineStackStruct LineStack; During initialization, as well as with each “release” of a finger from the screen, this stack is initialized to its original state by calling the following function:
void ClearCurrentStack() { LineStack.len = 0; // LineStack.num = 0; // , } Finger / stylus handling on the crossword grid is handled by the Redraw function, which returns true if the crossword is to be redrawn after processing, and false otherwise.
Redraw
/* jc - JCStruct DrawContext - -, , : jc_screen_x - x jc_screen_y - y cell_wh - jc_screen_w - jc_screen_h - */ bool Redraw(int x, int y) // x,y -- - { if (!jc->Resolved) // , if ((DrawContext.jc_screen_x <= x) && (x < DrawContext.jc_screen_x + DrawContext.jc_screen_w)) if ((DrawContext.jc_screen_y <= y) && (y < DrawContext.jc_screen_y + DrawContext.jc_screen_h)) { // int i = (x - DrawContext.jc_screen_x) / DrawContext.cell_wh; int j = (y - DrawContext.jc_screen_y) / DrawContext.cell_wh; // , , char n = GetNumberFromByte(jc->M[i][j]); if ((LineStack.len == 0) && (n == 0)) return false; // , if (GetFlagFromByte(jc->M[i][j]) > 0) return false; // , for (int s = 0; s < LineStack.len; s++) if ((LineStack.stack[s].x == i) && (LineStack.stack[s].y == j)) { // LineStack.len = s + 1; return true; } // , , ( ) if (LineStack.len == 0) { // LineStack.len++; LineStack.num = n; // , // LineStack.stack[LineStack.len - 1].x = i; LineStack.stack[LineStack.len - 1].y = j; return true; } else // , { // , // ( num) if (LineStack.len < LineStack.num) { // , , if ((abs(LineStack.stack[LineStack.len - 1].x - i) == 1 && LineStack.stack[LineStack.len - 1].y == j) || (LineStack.stack[LineStack.len - 1].x == i && abs(LineStack.stack[LineStack.len - 1].y - j) == 1) ) { // , , , // , if (n == 0 || LineStack.num == n && LineStack.len == n - 1) { LineStack.len++; LineStack.stack[LineStack.len - 1].x = i; LineStack.stack[LineStack.len - 1].y = j; return true; } return false; } // , if ((LineStack.stack[LineStack.len - 1].x != i) && (LineStack.stack[LineStack.len - 1].y == j)) { int len = abs(i - LineStack.stack[LineStack.len - 1].x); // int d = (i - LineStack.stack[LineStack.len - 1].x) / len; // ( ) for (int s = 0; s < len; s++) { if (LineStack.len < LineStack.num) { // if (GetFlagFromByte(jc->M[LineStack.stack[LineStack.len - 1].x + d][j]) > 0) { if (s > 0) return true; // - , else return false; // , } n = GetNumberFromByte(jc->M[LineStack.stack[LineStack.len - 1].x + d][j]); if (n > 0) // { if (n != LineStack.num) // , { if (s > 0) return true; // - , else return false; // , } else // , , .. n == LineStack.num { if (LineStack.num != LineStack.len + 1) // { if (s > 0) return true; // - , else return false; // , } } } LineStack.len++; LineStack.stack[LineStack.len - 1].x = LineStack.stack[LineStack.len - 2].x + d; LineStack.stack[LineStack.len - 1].y = j; } } return true; } // , if ((LineStack.stack[LineStack.len - 1].x == i) && (LineStack.stack[LineStack.len - 1].y != j)) { int len = abs(j - LineStack.stack[LineStack.len - 1].y); // int d = (j - LineStack.stack[LineStack.len - 1].y) / len; // ( ) for (int s = 0; s < len; s++) { if (LineStack.len < LineStack.num) { // if (GetFlagFromByte(jc->M[i][LineStack.stack[LineStack.len - 1].y + d]) > 0) { if (s > 0) return true; // - , else return false; // , } n = GetNumberFromByte(jc->M[i][LineStack.stack[LineStack.len - 1].y + d]); if (n > 0) // { if (n != LineStack.num) // , { if (s > 0) return true; // - , else return false; // , } else // , , .. n == LineStack.num { if (LineStack.num != LineStack.len + 1) // { if (s > 0) return true; // - , else return false; // , } } } LineStack.len++; LineStack.stack[LineStack.len - 1].x = i; LineStack.stack[LineStack.len - 1].y = LineStack.stack[LineStack.len - 2].y + d; } } return true; } return false; } else // , { return false; } } } return false; } When the finger / stylus is “squeezed out”, it processes the stack of the current line. It is necessary to understand whether the line is drawn correctly, i.e., to check it for correctness, and, if correct, to update the corresponding cells of the matrix.
CheckCurrentLineStack
/* , - , */ void CheckCurrentLineStack() { // , , // , , , if ((LineStack.len > 0) && (LineStack.len == LineStack.num) && (LineStack.num == GetNumberFromByte(jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y])) ) { // SetMatrixElement(jc, LineStack.stack[0].x, LineStack.stack[0].y/*, 1*/); // // , / [0 - , 1 - , 2 - , 3 - ] char l_prev, l_next; // , for (int i = 1; i < LineStack.len - 1; i++) { // if (LineStack.stack[i - 1].x + 1 == LineStack.stack[i].x) l_prev = 0; if (LineStack.stack[i - 1].x - 1 == LineStack.stack[i].x) l_prev = 1; if (LineStack.stack[i - 1].y + 1 == LineStack.stack[i].y) l_prev = 2; if (LineStack.stack[i - 1].y - 1 == LineStack.stack[i].y) l_prev = 3; // . if (LineStack.stack[i + 1].x + 1 == LineStack.stack[i].x) l_next = 0; if (LineStack.stack[i + 1].x - 1 == LineStack.stack[i].x) l_next = 1; if (LineStack.stack[i + 1].y + 1 == LineStack.stack[i].y) l_next = 2; if (LineStack.stack[i + 1].y - 1 == LineStack.stack[i].y) l_next = 3; l_prev = MAX(l_prev, l_next) * 10 + MIN(l_prev, l_next); switch (l_prev) { case 32: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] = jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_VERTICAL; break; case 31: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] = jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_LEFT_TOP; break; case 30: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] = jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_RIGHT_TOP; break; case 21: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] = jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_LEFT_BOTTOM; break; case 20: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] = jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_RIGHT_BOTTOM; break; case 10: jc->M[LineStack.stack[i].x][LineStack.stack[i].y] = jc->M[LineStack.stack[i].x][LineStack.stack[i].y] + LN_HORIZONTAL; break; } } // if (LineStack.stack[1].x + 1 == LineStack.stack[0].x) jc->M[LineStack.stack[0].x][LineStack.stack[0].y] = jc->M[LineStack.stack[0].x][LineStack.stack[0].y] + LN_RIGHT; if (LineStack.stack[1].x - 1 == LineStack.stack[0].x) jc->M[LineStack.stack[0].x][LineStack.stack[0].y] = jc->M[LineStack.stack[0].x][LineStack.stack[0].y] + LN_LEFT; if (LineStack.stack[1].y + 1 == LineStack.stack[0].y) jc->M[LineStack.stack[0].x][LineStack.stack[0].y] = jc->M[LineStack.stack[0].x][LineStack.stack[0].y] + LN_BOTTOM; if (LineStack.stack[1].y - 1 == LineStack.stack[0].y) jc->M[LineStack.stack[0].x][LineStack.stack[0].y] = jc->M[LineStack.stack[0].x][LineStack.stack[0].y] + LN_TOP; // if (LineStack.stack[LineStack.len - 2].x + 1 == LineStack.stack[LineStack.len - 1].x) jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] = jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] + LN_RIGHT; if (LineStack.stack[LineStack.len - 2].x - 1 == LineStack.stack[LineStack.len - 1].x) jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] = jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] + LN_LEFT; if (LineStack.stack[LineStack.len - 2].y + 1 == LineStack.stack[LineStack.len - 1].y) jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] = jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] + LN_BOTTOM; if (LineStack.stack[LineStack.len - 2].y - 1 == LineStack.stack[LineStack.len - 1].y) jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] = jc->M[LineStack.stack[LineStack.len - 1].x][LineStack.stack[LineStack.len - 1].y] + LN_TOP; DrawContext.need_save = true; } } Drawing a crossword and the current line
Drawing a crossword puzzle is divided into the following steps:
- Drawing shaded matrix cells;
- Drawing current line stack cells;
- Drawing lines on the filled cells of the matrix;
- Drawing lines on the stack cells of the current line;
- Drawing numbers on the cells.
In order not to unnecessarily overload the article with code, we will only list the listing itself from the interesting of the above points.
Drawing lines on shaded cells
if (jc->Resolved == false) // { // Iw2DSetColour(ColorSchema.JCCellLineColor); for (int i = 0; i < jc->W; i++) for (int j = 0; j < jc->H; j++) { n1 = jc->M[i][j] & BYTE_FLAG_PART; switch (n1) { case LN_HORIZONTAL: Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + 0, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1 ), CIwFVec2(DrawContext.cell_wh - 0, 3) ); break; case LN_VERTICAL: Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + 0), CIwFVec2(3, DrawContext.cell_wh - 0) ); break; case LN_RIGHT: Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + 0, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1), CIwFVec2(4, 3) ); break; case LN_LEFT: Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i + 1)* DrawContext.cell_wh - 4, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1), CIwFVec2(4, 3) ); break; case LN_BOTTOM: Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + 0), CIwFVec2(3, 4) ); break; case LN_TOP: Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1, DrawContext.jc_screen_y + (j + 1)* DrawContext.cell_wh + 0 - 4), CIwFVec2(3, 4) ); break; case LN_RIGHT_BOTTOM: // Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + 0, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1), CIwFVec2(DrawContext.cell_wh / 2 - 1 + 3, 3) ); // Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + 0), CIwFVec2(3, DrawContext.cell_wh / 2 - 1 + 3) ); break; case LN_RIGHT_TOP: // Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + 0, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1), CIwFVec2(DrawContext.cell_wh / 2 - 1 + 3, 3) ); // Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1), CIwFVec2(3, DrawContext.cell_wh / 2 - 1 + 3) ); break; case LN_LEFT_BOTTOM: // Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1), CIwFVec2(DrawContext.cell_wh / 2 - 1 + 3, 3) ); // Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + 0), CIwFVec2(3, DrawContext.cell_wh / 2 - 1 + 3) ); break; case LN_LEFT_TOP: // Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1), CIwFVec2(DrawContext.cell_wh / 2 - 1 + 3, 3) ); // Iw2DFillRect(CIwFVec2(DrawContext.jc_screen_x + (i)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1, DrawContext.jc_screen_y + (j)* DrawContext.cell_wh + DrawContext.cell_wh / 2 - 1), CIwFVec2(3, DrawContext.cell_wh / 2 - 1 + 3) ); break; } } } Checking the resolution of a crossword puzzle
Due to the fact that the correctness of each drawn line is checked at the time of its drawing, all existing lines comply with the three rules given at the beginning of the article. And this in turn means that to verify the resolution of a crossword puzzle, we just need to make sure that all the cells with numbers are painted over.
CheckJC
/* 0, , , */ int CheckJC(JCStruct * p) { for(int i = 0; i < p->W; i++) for(int j = 0; j < p->H; j++) if(GetNumberFromByte(p->M[i][j]) > 1) // , 1 , if(GetFlagFromByte(p->M[i][j]) == 0) // return 100 * (i + 1) + (j + 1); return 0; } You can play the application at the links below:
Black and white: Android , iOS
Colored: Android
Source: https://habr.com/ru/post/301184/
All Articles