Metromarathon Algorithm. As a Yandex analyst, I calculated that all stations can be visited in one day.

On May 12, my friends and I entered the Moscow metro with its opening in the morning and, without getting up, we visited all 199 stations currently available until the metro was closed. Why we did all this is not at all clear, but I will try to tell how it happened.

A long time ago, it seems, about a year ago my wife told me that she would like to somehow take a picture of all the metro stations in Moscow. I then joked that under such a case, you can calculate the optimal route that allows you to visit all the stations, straining to a minimum. I joked and forgot, but then I remembered in the winter and decided to try.

As I studied the issue, I found that the idea itself was not very new - in the New York subway, similar competitions have been held since 1966. As for the Moscow metro, the LJ user estrella-de-sur six months ago drove it 12 hours 36 minutes (estimated time - 11 hours 50 minutes) according to the rule “one step per station”. But we had another task - we wanted to get out at each station and, if possible, take a nice picture of it. This meant that in most cases we would have to wait for the next train on it. Based on this, I built the calculation.

Warning: if you know how to solve the traveling salesman problem on 200 nodes (with or without genetic algorithms), you are most likely being expected elsewhere. You can just scroll through the post and see the pictures.

Where to get the data

First of all, for such a task it was necessary to digitize the graph of the metro (nodes - stations, edges - crossings and transitions) and supplement its elements with various useful information: for stations - geographical coordinates, opening-closing times and intervals of trains at different times of the day; for edges - the time of a ferry or transition between stations.

There are a lot of stations in Moscow (Salaryevo had not yet been opened at that time, but it was still enough), and I didn’t want to do it all at all. Then I turned to the site Yandex . Metro . It was just right for a start, but this service uses average time estimates, and for serious calculation it was necessary to have more accurate information. Then I remembered a couple of pretty the ancients programs with national time measurements - pMetro and mMetro - this, if anyone knows, such desktop calculators of metro routes. The first almost ceased to be officially updated in 2011, the second - even earlier, but everything is better than nothing.

Among the files in the pMetro folder was Moscow.pmz, which actually turned out to be a regular zip-archive with a bunch of files in an archaic .ini format. Almost all the necessary information was found there (some of the most recent stations were missing from the diagram). I made a one-time parser for all of this in tsv, and I dabbled the missing stations and spans, “ringing” the timings for them on Yandex.Metro . I took the coordinates of the new stations from Wikipedia articles.

The scheme finally turned out like this (the projection, of course, is not Mercator, but conveys the essence):

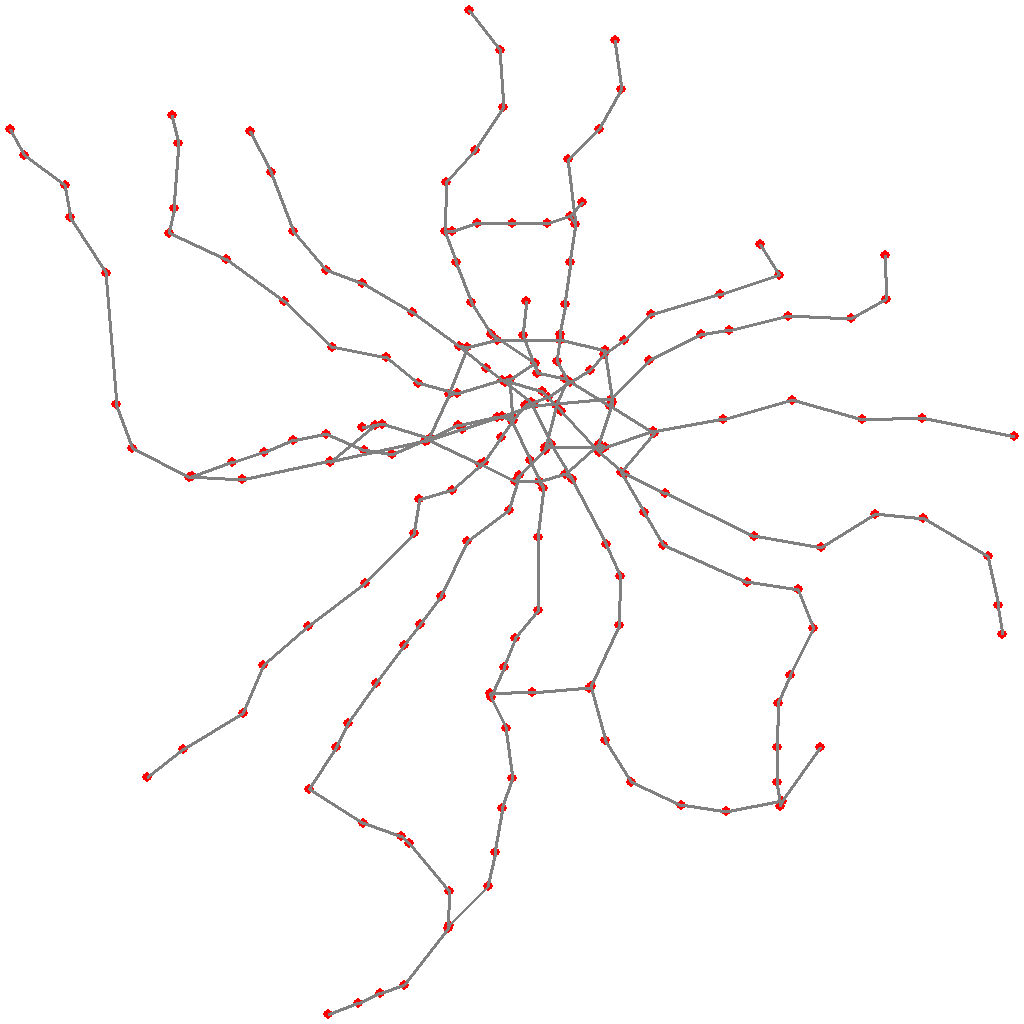
(here I also drew the monorail line, but, later, it was decided to abandon it)

Now I had to try to fly with all this.

Salesman genome

So, it was necessary to solve the classical traveling salesman problem in the formulation on an incomplete graph over 200 vertices. Ancestral experience teaches us that this task is NP-complete and even, probably, transcomputational . Translated into Russian, the first means, approximately, that we don’t know how to find its best solution, except for enumerating all the possible answers, and the second, that we will have to sort out for quite a long time (no less than billions of years). In practice, however, one can try to organize the search in such a tricky way, in order to gradually find more and more good solutions and stop “on readiness.

Before proceeding, I note that the first normal impulse of a healthy person is to attempt to pave the optimal route on their own, manually, or at least jot it down with large strokes, and then bring it up automatically. But since in our case, the cost of the edge depends on its position in the route (ie, on the time of day), and 51 stations are located on a fairly dense section of the graph (inside and on the ring, including transplants), the passage of which essentially depends on the entry and exit points using common sense is not easy. It is also interesting that depending on whether we are going to go out at each station and wait for the next train, or not, the optimal route may be completely different (since the intervals of trains on different lines are different).

But we will continue. As I have already said, you can organize an exhaustive search in such a way as to gradually find more and more good solutions, and if we do not need guarantees that the solution found is the best, we can stop at any moment when we consider that the current best result is “sufficient good for us. One of the ancient classical approaches in such a situation is the use of genetic algorithms .

This is a fairly simple idea of ​​the times of the past popularity of evolutionary theory: we will describe each solution with some vector (“genome”), formulate the quality function of a specific genome (in our case, the time it takes for the entire route), and start the evolution: add random mutations, or even force the best of "Individuals", of course, mate. Several thousand generations of such eugenics - and we have a good one superman route.

But the devil, as usual, in the details. First, it is necessary to choose a good representation of information in the genome. You can, for example, make a vector genome with the numbers of all stations in the order they are followed in the route. What is bad? Genomes of different routes will be of different lengths - it will be inconvenient for them to interbreed. And among the random values ​​of the genome there will be many invalid routes - such that do not allow to visit all the stations. In other words, in the space of genome values, the concentration of really possible candidates will be low - which means we will have to individually check each candidate for validity, spending too much time on it.

It is much more convenient to declare a permutation of length 200 genome - i.e. such a vector of length 200, in which each station occurs only once. However, with this approach, stations in the route may be adjacent, between which there is no direct connection. It does not matter - we can go to the full graph by calculating the shortest route along the graph between each pair of vertices (in the forehead it is easy to do for O (| V | ^ 3) operations, which in our case is not so much). It is important to note that this shortest route can also be different at different times of the day, taking into account the dynamics of the schedule. Therefore, it makes sense to calculate such tables for each slice of the interval schedule.

Secondly, you need to poshamanit with different types of mutations and crosses. There is not much science here, continuous empiricism, aimed mainly at ensuring, on the one hand, fast convergence, and on the other, the possibility of getting out of evolutionary deadlock local optimum. As a result, I stopped at a set of the following transformations:

• random shuffling of the random genome interval is a quick mutation, but not very accurate; in the final stages of evolution, it can improve a good solution with a very low probability.
• mirror image of the random interval of the genome - it can be useful for strong changes (exit from the local optimum), with chances to preserve some order (high quality) of the route in the context of our task
• rearrangement of X pairs of random values ​​in the genome in some places is a good mutation, but slow, you cannot get out of the impasse on it.
• crossing (“crossover”) of two genomes - first choose the point of crossing on the genome, cut off the tails of our genomes and change their places. After that, we can get an incorrect route - so we uniquely identify the result and add all the lost nodes, for example, to random places in the genome.

So, at each iteration, we substitute some subset of the best individuals with various mutations and form a new generation from their descendants, getting some completely random routes to them so as not to fall victim to inbreeding. Calculation of such an evolution of 50,000 generations with a knee-length python script takes on average 20 minutes on my home desktop. And so it was not so boring to wait, you can spy on him in the dynamics, drawing the best individual of each, say, the hundredth generation. Here is a small gif showing the favorites of the first few thousand generations in the cycle:

The sequence of steps in the route corresponds to the gradient of gray. It can be seen that at the very beginning the route changes rather chaotically, then quickly goes to the local optimum and begins fine-tuning on trifles. And if you wait long enough (already outside the gifs), you can, if you're lucky, see how, from time to time, evolution jumps to a new, deeper optimum and continues to optimize there.

The important point is that if we see that independent optimization runs give us significantly different answers, even if they are similar in quality, it means that it is likely that we have not found the global optimum. But we are satisfied with its rather good approximation, which you can try to get by “multi-start” - run the algorithm many times (including with different settings, for example, setting the beginning and end of the route equal to different fixed branches) and choose the best of the observed results.

To extend the suspense a bit, I’ll show you the route, which, according to my calculations, took the second place (go from light to dark):

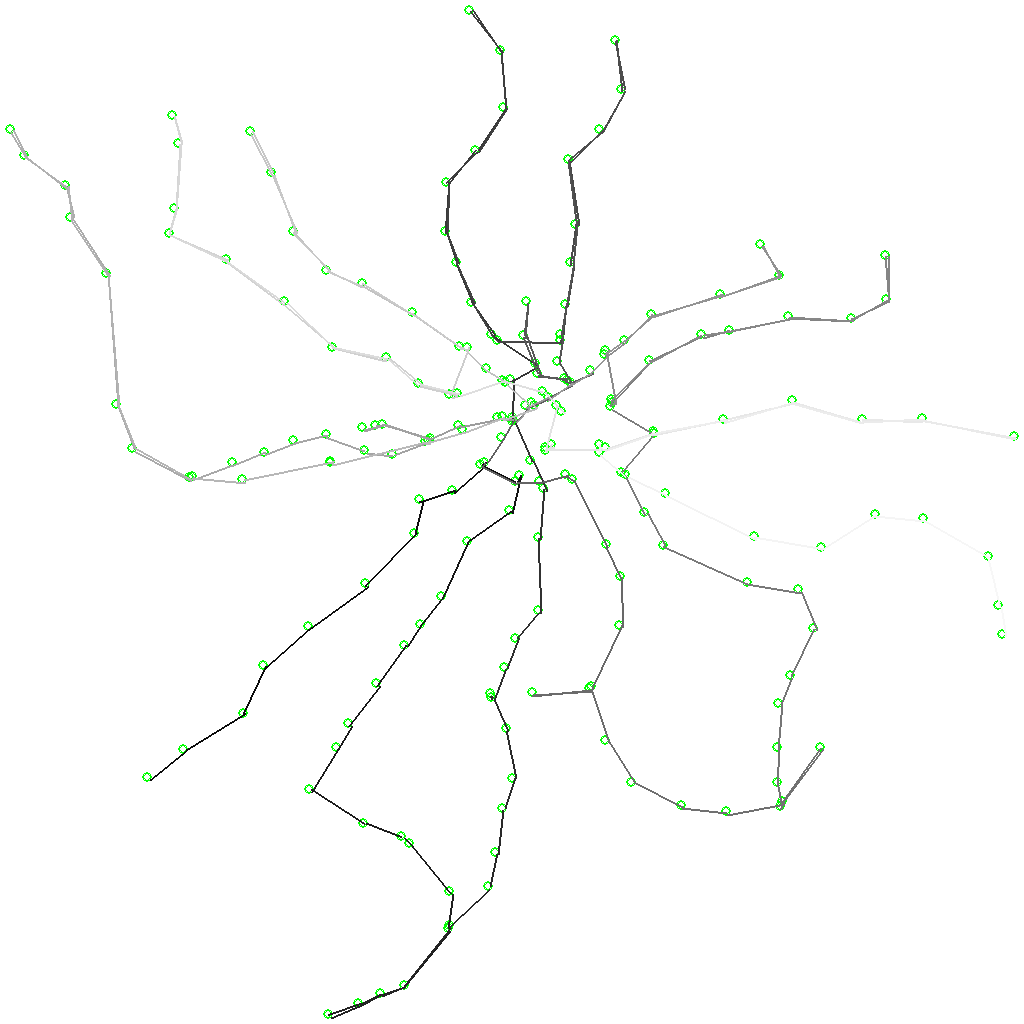
And the final assessment of the duration of the best route turned out to be 19 hours 51 minutes. Let me remind you that the interval of work of the Moscow metro is approximately 20 hours, and I took all the initial data about the intervals of trains following from amateur measurements. If I had a route at 10 or 40 o'clock, everything would have been clear one way or another. But here the margin was only 9 minutes with an unknown (but obviously not small) error.

Back to the real world

At about this point, the idea to test this route became stronger in practice. By that time, several of my friends were already aware of my strange research. A couple of them turned out to be quite insane, and now - we put together a team to check out the battle. But, since the risks of “not getting there” in the allotted time were quite high, I decided to first check out a number of alternative options.

Option "Return the monorail." A curious fact: it takes less time to travel from Timiryazevskaya to the VDNH on the subway with a transfer through the ring than with transfer to the monorail and back (according to pMetro, without having to go out at each station). Option rejected.

Option "Add ground transportation." The idea is that you can try to move between the end of different lines on public transport by land. For data on transfers to land transport, I went to Dima Kryukov from Yandex. Schedules. It turned out that we don’t have accurate information on transfers between the metro and ground transport, but there is detailed information on all land stops and routes of buses / trolley buses / trams.

There is nothing to do, I had to do the stops with stations by names. There were found quite a few underwater rakes, which are not very interesting to talk about. I can only say that in Moscow there were exactly 999 ground stops, called “in honor of” one or another metro station (not counting several “metro-bridges”, “metrodepo”, “metro-towns” and others). And yet, some of the stops are still named after the already renamed metro stations. But this stuff.

Here, by the way, is a scheme with found ground “chords”:

But, anyway, when I added estimates for the exit time + ground transportation expectations + journey + return to the subway, it turned out that these “chords” do not really help - the concept of “metro-trip” loses its original purity, and the calculated gain is only 15-20 minutes. Option rejected.

Option "Add a taxi." In fact, this is a modification of the previous version, but instead of public transport it is supposed to use a taxi. For this, I selected for each end stratum of each radial branch the geographically closest stations on neighboring branches for these ends, and added “chords” for such pairs with a time estimate using Yandex.Navigator.

After optimizing, this was an interesting route with four chords:

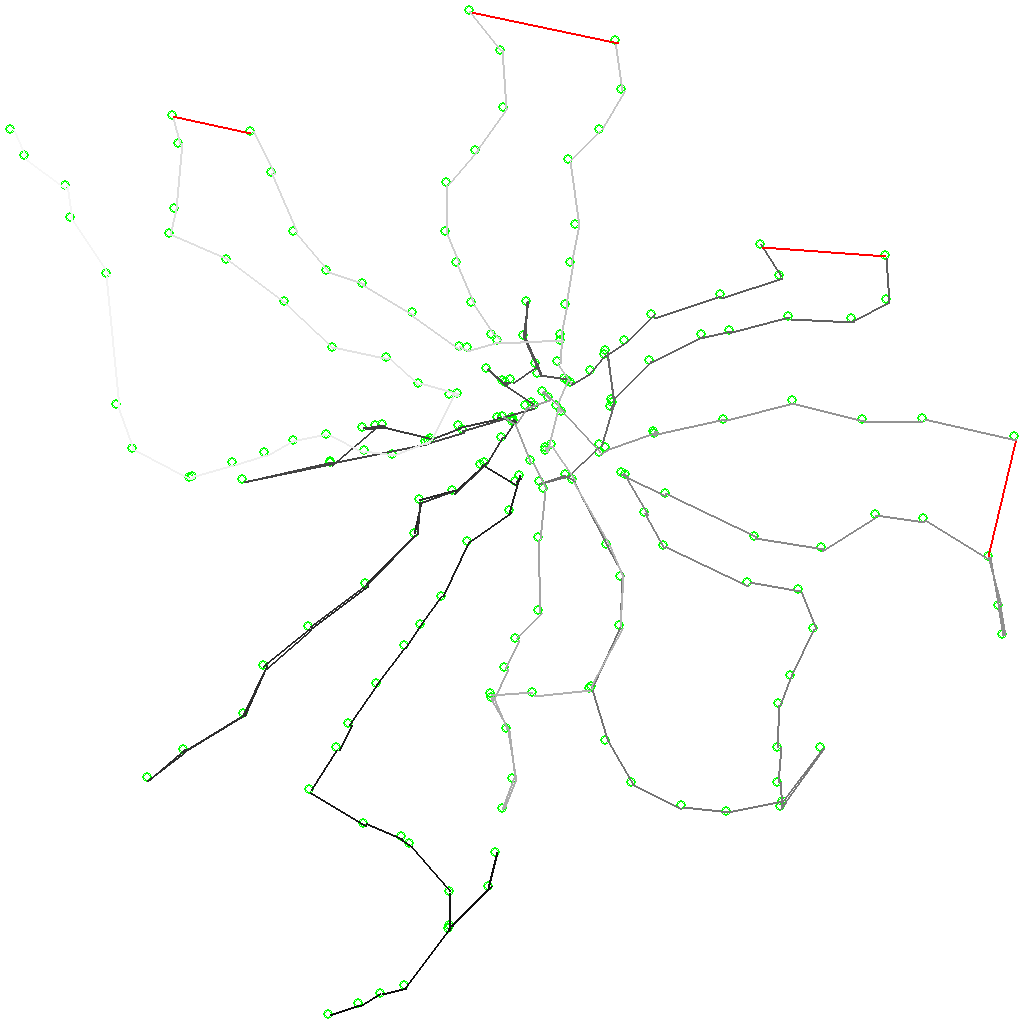
This route was estimated to be about 30 minutes shorter than my optimal one. Option rejected as "not sporty."

Results

After a heated debate, we decided to go the best route without the “chords” and exit at each station. In the end, if we wanted to just nominally go around all the stations, we could not leave the car at all and get a time of about 12 hours. But the Moscow metro is considered to be one of the most beautiful metros in the world, so it is better to enjoy part of the stations than to visit everything, but not to see anything.

The mood was serious, so at this stage we turned to the Moscow Metro and validated our route with their help. We were assigned a special attendant from the Passenger Mobility Center, were allowed to take photos and video and even occasionally allowed to use office toilets, which, as it turned out, are at each station.

So, on May 12, my friends and I entered the Moscow metro early in the morning and, without getting up, we visited all 199 stations currently available until the metro was closed. Why we did all this is not at all clear, but this is not the point, the main thing is that we succeeded.

We did not have the task to drive all the metro "for a while", rather we wanted to really see all the stations in one day. We went out at each station, took pictures (a couple of hundred photos can be found in our various tapes on social networks ) and drove on - sometimes on the same train, and sometimes skipping several trains to a row if the station was so interesting that we wanted to there is more time on it.

Our final time was 16 hours 22 minutes, and we are pleased to publish our route , so that anyone can try to improve this time.

It is with great pleasure that I thank everyone who somehow helped us in this crazy undertaking — and the team of marathoners themselves, and the online support team, and the many people who helped us in the training.
Detailed thanks can be found in our closing post on FB .