A few thoughts on comparing statistics

Comparing an entity with known objects is one of the most obvious ways to classify. The more an object resembles representatives of a set known to us, the higher the probability that it belongs to this set. For comparison, we need specific metrics (numbers suitable for mathematical processing). But as you understand, visually analyzing such matrices is not very convenient.

For easy perception, you must display this data in a graphical form. The first thing you can try is a “mosaic”. The size of its blocks will reflect the value of the corresponding object metric. Since our matrix consists of identical objects, a “strange” object should stand out against the general background. However, the difference of its metrics is not so strong, therefore, the sizes of “strange” blocks will not be radically allocated. This can best be understood from the following example (the matrix and its display in the form of a “mosaic”):



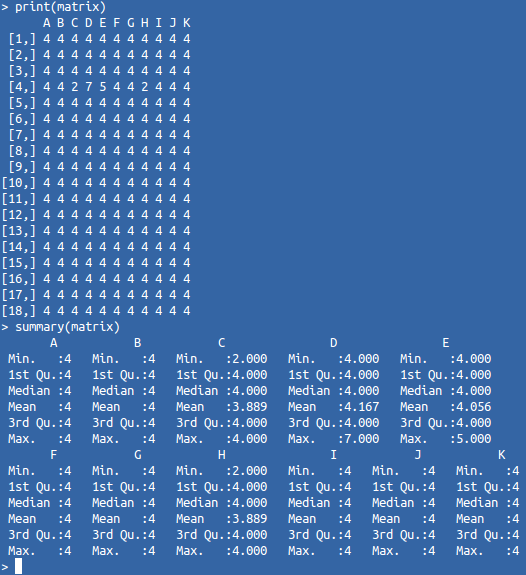
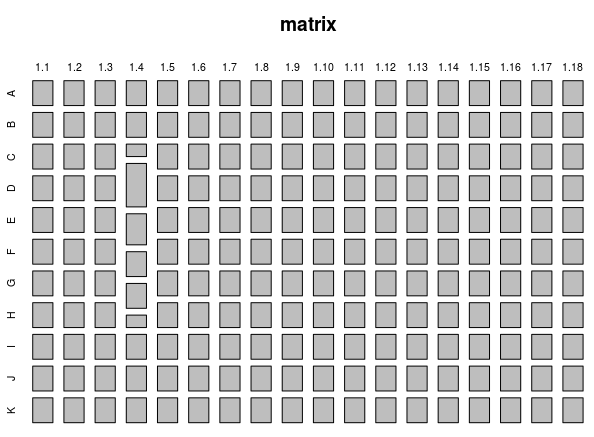
It is well known that a person can very quickly find an object with a different color on a uniform background. Therefore, if we display this matrix on a heat map, then similar elements form a single background, and different elements will contrast well with the homogeneous majority.


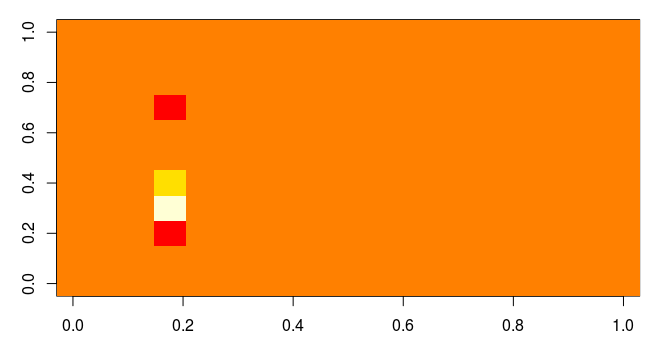
Naturally, a person very well recognizes not only colors, but also the shape of objects. If you display the matrix in the form of a three-dimensional perspective, any deviations from the total mass of typical objects will be quite clearly visible.

')
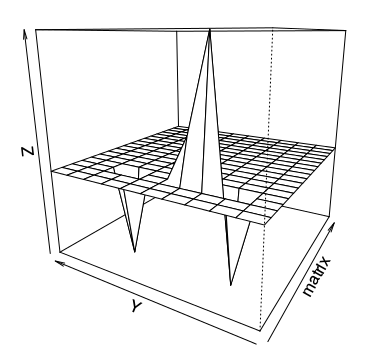
Knowing the signs of different objects, it is possible to form a subset that consists only of "strange" objects. Then you can display a diagram of the difference between the object from the subset and the typical object of the set.


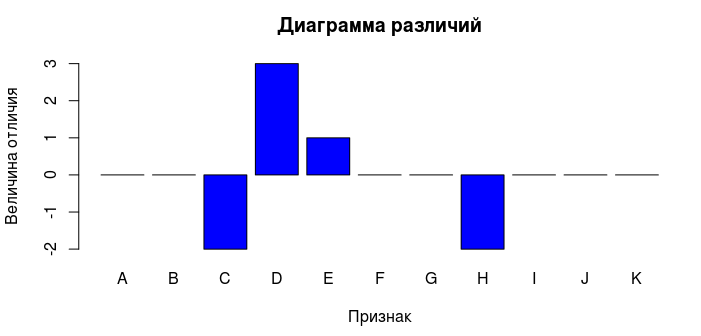
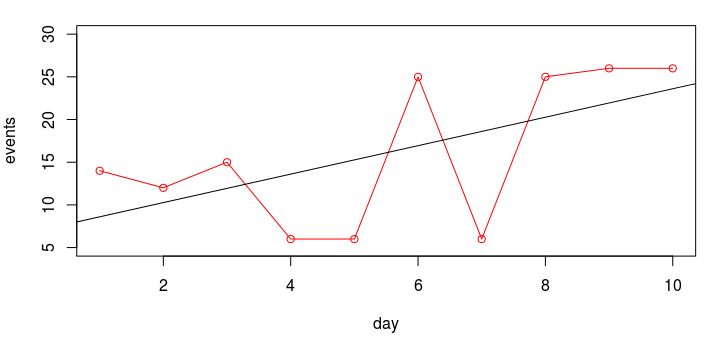
Of course, it would be logical to study the behavior of the indicators of interest in more detail. As you know, the linear correlation coefficient does not always help to find the dependence of the variables, however, we can build a graph for the desired period of time. Visually assessing the correlation will be much easier. But we will not just build a graph, but we will try to perform an elementary linear regression analysis. Consider a small example. There is a hypothesis that an increase in one indicator leads to an increase in the value of a variable dependent on it. Let's try to display this graphically:


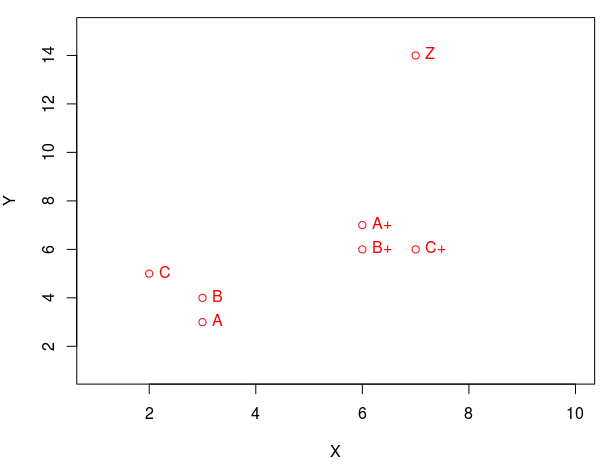
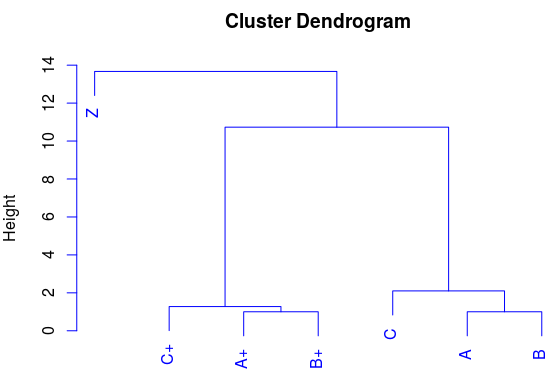
There are situations when we can find similarities in points in space. If you display two signs in the form of coordinates (by abscissa and ordinate), then you can see that some points are collected in groups (form clusters). We see that the points (A, B, C) are grouped into one group, and the points (A +, B +, C +) into another group. And I will add a point Z, which should not fall into any of the clusters. This is such a "lone wolf." Hierarchical cluster analysis will help us to more clearly visualize the similarities. Let's compare the display of points on the graph and on the dendrogram:



This is a fairly universal approach, which is not rarely used in the visual assessment of relatively small amounts of data. Many mathematical systems already contain the implementation of the previously mentioned methods, for example, in a well-known R programming language, the solution of such problems may look like this:

#     matrix <- as.matrix(read.csv(path), ncol=11, byrow = TRUE) print(matrix) summary(matrix) #    mosaicplot(matrix) image(matrix) persp(matrix, phi = 15, theta = 300) #      dataset <- subset(matrix, matrix[,"A"] == 4 & matrix[,"C"] < 4 & matrix[,"D"] > 4) print(dataset) #       a <- as.vector(dataset[1,], mode='numeric') b <- as.vector(matrix[1,], mode='numeric') diff <- a - b barplot(diff, names.arg = colnames(matrix), xlab = "", ylab = " ", col = "blue", main = " ", border = "black") #    day <- c(1:10) events <- c(14, 12, 15, 6, 6, 25, 6, 25, 26, 26) cor.test(day, events) plot(day, events, type = "o", ylim=c(5, 30), col = "red") abline(lm(events ~ day)) #     matrix <- matrix(c(3, 3, 2, 6, 6, 7, 7, 3, 4, 5, 7, 6, 6, 14), nrow=7, ncol=2) dimnames(matrix) <- list(c("A", "B", "C", "A+", "B+", "C+", "Z"), c("X", "Y")) plot(matrix, col = "red", ylim=c(1, 15), xlim=c(1, 10)) text(matrix, row.names(matrix), cex=1, pos=4, col="red") plot(hclust(dist(matrix, method = "euclidean"), method="ward"), col = "blue")