Why are ten nuggets worth as much as twenty?

My latest business The Crumbs is becoming increasingly popular. At Dartmouth College, students without cars face difficulties in transporting necessary items. Therefore, I launched a local delivery service, partly to help students access Walmart, CVS and various fast food outlets. And his main goal is to transfer all the profits to a local homeless shelter , where I worked as a volunteer for many years.

But this post is not about The Crumbs. He pro Chicken McNuggets.
')
Three and a half weeks ago, adding the ability to work with fast food in my The Crumbs, I downloaded the price list with prices for fast food. But when our team went live to the nearest McDonalds, she saw that the prices for the nuggets were as follows:

10pcs - $ 6.40
20pcs - $ 6.40
40pcs - $ 11.51

In New Hampshire, McDonalds takes the same amount of money for both 10 and 20 Nuggets.

I was surprised and began to look for an explanation of this fact.

There are several different plausible versions (for example, that 20 pieces are too many for one person), but they all break down on the simple question “why won't McDonald’s drop the price of 10 nuggets, or raise the price of 20 nuggets?”. As a result, I came up with three fairly convincing explanations for this fact.

1. Distracting product

In the book “ Predictably Irrational ” by author Dan Ariely (Dan Ariely), which explains behavioral economics, a professor of economics talks about a funny psychological trick used in a subscription to The Economist magazine. Readers were offered two options:

Web only: $ 59
Web and print: $ 125

Of all those who bought a subscription, 68% bought only the web version - a more economical option.

Then the magazine added a third option:

Web only: $ 59
Print version only: $ 125
Web and print: $ 125

The option “Print version only” looked erroneous - it offered a very strange alternative to the comprehensive version “Web and print version” at the same price. But at the same time, 84% of subscribers bought the more expensive version of "Web and print version", which proved that adding a new version was not at all a mistake.



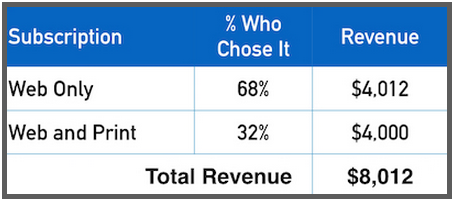
The meaning of this option is not to buy it - it served as a point of comparison for the option “Web and print version”, and compared to it, it already seemed more attractive. A little trick helped increase sales by almost 50%.

Therefore, perhaps, this is what McDonalds is trying to do:

10pcs - $ 6.40 (distracting product)
20pcs - $ 6.40
40pcs - $ 11.51

True, with an example from the book there are differences. Instead of attracting buyers to a more expensive option, a distracting product attracts them to a less expensive one. Does this not reduce sales?

Therefore, I continued to search for options.

2. Losses on leaders

A post in Quora tries to explain it like this:

Many vendors, including all fast foods, have a trick: to offer a small group of popular products at low prices and with low margins. Their task is only to lure you to the point of sale, in the hope that with them you will order other products, especially those with a much higher margin, with the result that the total profit will even out.

Approximately the same explanation can be found on Reddit .

Even if McDuck does not earn from selling 20 Nuggets as much as selling 10, you have already reached the point of sale. Salty and seasoned nuggets will encourage you to buy a drink or potatoes, the profits from which are much greater.

But this also raises questions. Is nuggets not a profitable product? Burger King sells 10 nuggets for $ 1.49, which means they are not as expensive to manufacture at all. Perhaps they are just dumping, but it still seems rather strange that with such huge sales, McDonalds does not make money on nuggets.

3. The paradox of choice

This paradox was illuminated by Professor Barry Schwartz - too many options make it difficult to choose. When people spend a lot of time on a choice and weigh a lot of pros and cons, their expectations increase and their chances to sell them something lower.

Perhaps by offering only two real options instead of three, and making so that 20 nuggets look like a “good enough” choice, the institution helps buyers make choices quickly.

But the rest of the McDonald's menu contradicts this conclusion. Too many sizes, tastes, and even the ability to change the standard recipe - it's hard to believe that this paradox is generally taken into account. With this choice, reducing the number of options by just one will not improve the situation.

What we have there with real numbers?

Unfortunately, McDonalds does not publish detailed information about sales. But with the help of data collected during the work of The Crumbs project, we, assuming (although this is not entirely correct) that we are dealing with an average sample of customers, we can conduct a small analytics.

And here are our statistics:



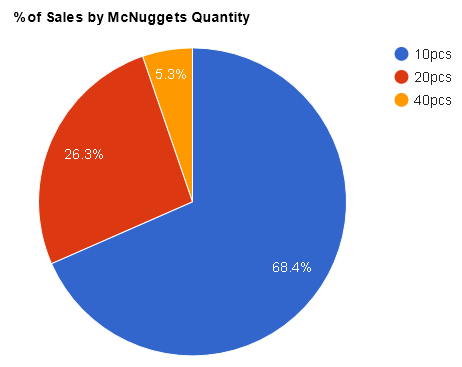
Shtaaaaaaa !?

People not only prefer 10 nuggets, they buy them much more often than 20 pieces - although they have the same price.

So why the allegedly distracting product turns out to be the most popular? We thought for a very long time, but did not reach a definite conclusion.

Perhaps the solution lies in the mixture of the above explanations. Maybe 40 nuggets are just a distracting product that no one buys, and then 20 nuggets look like a more logical choice that attracts people to the point of sale, after which they buy products with higher margins ... Maybe somewhere there is an answer hidden .

PS1: Riddle McChiken

I sat with a calculator and got that it’s more profitable to buy nuggets in McDonalds for buying nuggets. Sandwich Makchiken weighs 63 grams and contains better quality poultry meat than nuggets - so it is more economical to buy macchain. Of course, you have to cut pieces of chicken from macchiken into smaller pieces - but do not forget about the economic benefits.

PS2: A theorem named after the nuggets.

In school years, I participated in the Mathematical Olympiad , and there I met an interesting mathematical problem.

Then nuggets were sold only at 9 or 20 pieces. And the question was: what is the maximum amount of nuggets you cannot order?

It turned out that there is a general method for solving such problems. The Nagets theorem says that you can replace the numbers 9 and 20 by two arbitrary prime numbers a and b, and the solution to the question will be like this: ab - a - b.

Therefore, the greatest number of nuggets that cannot be bought: 20 * 9 - 20 - 9, or 151 nuggets. Any number greater than this can be made up of a combination of 9 and 20.