Tasks with dominoes on interviews
From personal experience, I can say that tasks that are somehow related to the dominoes of any surfaces are quite popular at interviews. Conditions may vary, but the essence of all remains the same.
There is a chessboard 8 by 8 cells, the lower left and right upper corners of which are cut off.

Is it possible to completely cover such a board with dominoes of size 2 × 1 square?
An even number of cells (62) remains on the board, so at first glance a solution is possible. However, let's do one very simple thing:
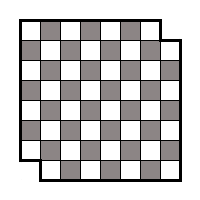
We painted the cells through one. Now everything becomes obvious. Each domino can occupy strictly two cells: one white and one black. Other options are not given. We look at which cells on the board are cut off - both are black, respectively, we have 32 white and 30 black cells and it is not possible to completely cover such a board.
The conditions of the problem may vary, but in general, the tasks for possibility-impossibility are immediately apparent.
')
There is a big cube of cheese 3x3x3 consisting of 27 identical cubes of cheese and a mouse, which eating one cube is taken to be adjacent to it on the edge of a cube of cheese. Can the mouse completely eat all the cheese, if the central cube is replaced with an inedible model?
The task is the same, only in space, not on the plane. We count the cells: in the initial scenario, this is 14 by 13, after the central cube is removed: 14 by 12 and as a result, there is no solution.
The next most popular are the tasks of counting the number of solutions.
Two boards are given:


On each cut 2 cells. Number of options for dominoes covering which of the boards is bigger In both cases, cells of different colors are cut out, so that all the knowledge with coloring from the previous examples will not help us here. There is little time left for interviews on the tasks, so you need to look for some kind of clue. And she is. Exclude from the first option, all coatings containing the cut cells of the second board, and from the second option - the first. (If this is easier to imagine, then we can assume that the cut cells were initially covered with a domino - which cannot be moved, and it is obvious that in this way we bring the boards to an identical state and the number of coating options will be identical too). After that, consider the lower corner of 3 by 2 cells. In the second embodiment, the left lower cell can be covered in only one way. Let us compare the first board version with this coating:

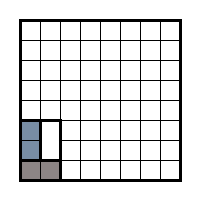
The remaining part except for this angle is identical, respectively, and the number of coatings is also identical. Thus, each variant of the second board covering is associated with the first board covering option. However, in the first case it is also possible to have all the dominoes arranged vertically, not corresponding to any variant of the second board. Consequently, the number of options for covering the board with cells cut in the corner is larger.
Find the number of options for dominoes covering 2xN cells.
Let her cover X (N) ways. Consider the option of covering the left upper cell:
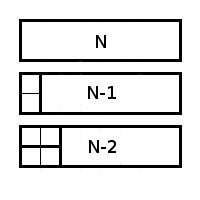
The remaining part in the first case can be covered with X (N-1) methods, and in the second, obviously, X (N-2).
Since all coverage options are listed and none of them will match, we get the equation X (N) = X (N-1) + X (N-2)
X (1) = 1, X (2) = 2, and X (N) will be equal to N + 1 number of the Fibonacci sequence.
Write a program that calculates the number of ways to cover the board 3xN cells dominoes.
I must say at once, perhaps, for this example, there is also an optimal solution, but I will go here from private solutions to general ones. In fact, all that is behind such tasks can be represented by a bipartite graph , one of the sets of vertices is black cells, and the other is white. Covering with dominoes is nothing more than the maximum matching of such a graph. Various algorithms (for example, Kuhn) can be used to search for it, and counting the number of options is a bit more complicated. In any case, it is outside of this article.
In conclusion, for demonstration, the implementation of the algorithm “head on” on python:
Example 1
There is a chessboard 8 by 8 cells, the lower left and right upper corners of which are cut off.

Is it possible to completely cover such a board with dominoes of size 2 × 1 square?
An even number of cells (62) remains on the board, so at first glance a solution is possible. However, let's do one very simple thing:

We painted the cells through one. Now everything becomes obvious. Each domino can occupy strictly two cells: one white and one black. Other options are not given. We look at which cells on the board are cut off - both are black, respectively, we have 32 white and 30 black cells and it is not possible to completely cover such a board.
The conditions of the problem may vary, but in general, the tasks for possibility-impossibility are immediately apparent.
')
Example 2
There is a big cube of cheese 3x3x3 consisting of 27 identical cubes of cheese and a mouse, which eating one cube is taken to be adjacent to it on the edge of a cube of cheese. Can the mouse completely eat all the cheese, if the central cube is replaced with an inedible model?
The task is the same, only in space, not on the plane. We count the cells: in the initial scenario, this is 14 by 13, after the central cube is removed: 14 by 12 and as a result, there is no solution.
The next most popular are the tasks of counting the number of solutions.
Example 3
Two boards are given:


On each cut 2 cells. Number of options for dominoes covering which of the boards is bigger In both cases, cells of different colors are cut out, so that all the knowledge with coloring from the previous examples will not help us here. There is little time left for interviews on the tasks, so you need to look for some kind of clue. And she is. Exclude from the first option, all coatings containing the cut cells of the second board, and from the second option - the first. (If this is easier to imagine, then we can assume that the cut cells were initially covered with a domino - which cannot be moved, and it is obvious that in this way we bring the boards to an identical state and the number of coating options will be identical too). After that, consider the lower corner of 3 by 2 cells. In the second embodiment, the left lower cell can be covered in only one way. Let us compare the first board version with this coating:


The remaining part except for this angle is identical, respectively, and the number of coatings is also identical. Thus, each variant of the second board covering is associated with the first board covering option. However, in the first case it is also possible to have all the dominoes arranged vertically, not corresponding to any variant of the second board. Consequently, the number of options for covering the board with cells cut in the corner is larger.
Example 4
Find the number of options for dominoes covering 2xN cells.
Let her cover X (N) ways. Consider the option of covering the left upper cell:

The remaining part in the first case can be covered with X (N-1) methods, and in the second, obviously, X (N-2).
Since all coverage options are listed and none of them will match, we get the equation X (N) = X (N-1) + X (N-2)
X (1) = 1, X (2) = 2, and X (N) will be equal to N + 1 number of the Fibonacci sequence.
Example 5
Write a program that calculates the number of ways to cover the board 3xN cells dominoes.
I must say at once, perhaps, for this example, there is also an optimal solution, but I will go here from private solutions to general ones. In fact, all that is behind such tasks can be represented by a bipartite graph , one of the sets of vertices is black cells, and the other is white. Covering with dominoes is nothing more than the maximum matching of such a graph. Various algorithms (for example, Kuhn) can be used to search for it, and counting the number of options is a bit more complicated. In any case, it is outside of this article.
In conclusion, for demonstration, the implementation of the algorithm “head on” on python:
from itertools import combinations
#
#
# , 2x2 :
# 1 2
# 3 4
# :
# mat = [
# [0, 1, 1, 0],
# [0, 0, 0, 1],
# [0, 0, 0, 1],
# [0, 0, 0, 0]
#]
# 1 => 2, 1 => 3, 2 => 4, 3 => 4
# ( . 3 => 1 )
#
N = len(mat)
#
all_edges = combinations(xrange(N), 2)
#
edges = [(x,y) for x,y in all_edges if mat[x][y]]
#
matchings = [tuples for tuples in combinations(edges, N/2) \
if len(set(reduce(lambda x, y: x+y, tuples))) == N]
print len(matchings)
# , O(N!)Source: https://habr.com/ru/post/285346/
All Articles