How to hire the best engineers without killing yourself
Garena , in which I am currently working, is in the process of growing and I am engaged in hiring engineers, system administrators and similar personnel in order to satisfy the appetites of the growing platform and to meet the plans and deadlines for the release of products. The problem that I constantly encounter is that not only our company is engaged in the search and hiring of engineers. This is especially true now, when many companies have published their annual bonuses (or lack thereof) and unsatisfied ordinary employees of companies join the ranks of applicants. In other words, musical chairs with companies and engineers gather in a pile.
“Musical chairs” (children's play; children go to music around the row of chairs; when the music stops, the players rush to hold chairs, which are one less than the playing ones)
Needless to say, this is the cause of certain difficulties with hiring. It is gratifying that there are many candidates. However, the flip side of this fact is the problem of maintaining a highly qualified engineer with an adequate mindset within the framework of a growing start-up. At the same time, the selection and approval of the candidate must be quick, as the delay, even with a partially suitable candidate, is fraught with its loss within one or two days.
It makes me wonder - which way is better to go if you have a large list of candidates and, in the end, choose the best engineer or, in any case, who is among the best of this list.
')
In the book “ Why Flip a Coin: The Art and Science of Good Decisions ,” HW Lewis wrote about a similar (albeit more stringent) problem with acquaintance. Instead of selecting candidates, the book talks about choosing a wife, and instead of conducting an interview, the problem of dating is considered. However, unlike the book, where it is assumed that you can only meet with one person at a time, in my situation, I obviously can interview more than one candidate. However, the problems that arise are largely unchanged, if I interview too many candidates and spend too much time making decisions, they will be intercepted by other companies. Not to mention the fact that I will probably die before my death from an overdose of intercourse.
In the book, Lewis proposed the following strategy - let's say we choose from a list of 20 candidates. Instead of interviewing everyone, we randomly select and interview 4 candidates and select the best from this sample list. Now, having this best of these 4 candidates in stock, we interview the rest of the list one by one until we meet someone better and, as a result, we hire this candidate.
As you guessed, this strategy is probabilistic and does not guarantee the selection of the best candidate. In fact, there are 2 worst case scenarios. First, if we randomly selected the 4th worst candidates as a sample list and the first candidate selected from the rest of the list is the 5th worst one, then we will hire the 5th worst candidate. Not good. Conversely, if the best candidate is on the sample list, then we risk holding 20 interviews and then losing this best candidate, since the whole process took too much time. Bad again.
So is this a good strategy? In addition, what is the optimal size of the list (total number of candidates) and sample list we need in order to get the most out of this strategy? Let's be good engineers and use the Monte Carlo simulation to find the answer.
Let's start with the strength of the list of 20 candidates, and then sort out the sample list from 0 to 19. For each sample list, we find the probability that the candidate we choose is the best candidate on the list. In fact, we already know this probability, if the sample list is 0 or 19. If the sample list is 0, the first candidate we interview will be selected (since there is no one to compare), so the probability is 1/20, and is 5%. Similarly, with the sample list equal to 19, we will have to choose the last candidate and the probability of this is also equal to 1/20 and is 5%.
Here is a ruby code that simulates this. Run the simulation 100,000 times to calculate the probability as accurately as possible, and save the result in the CSV file optimal.csv
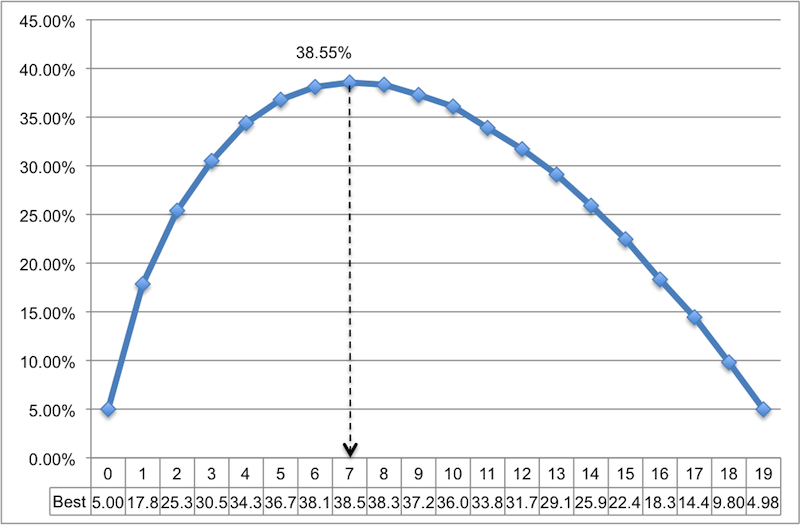
The code is quite self-evident (especially with all the comments), so I will not go into details. The result is shown below in a linear graph, after opening and marking the file in MS Excel. As you can see, if you select 4 candidates as a sample list, you will have about 1 chance out of 3 that you choose the best candidate. The best odds are if you select 7 candidates as a sample list. In this case, the probability that you choose the best candidate is about 38.5%. It doesn't look very good.
But, to be honest, in the case of several candidates I do not need that the candidate be “the best” (in any case, such assessments are subjective). Suppose I want to get a candidate in the top quarter of the list (top 25%). What are my chances then?
Here is the revised code that models it.
In the Optimal.csv file, we added a new column, which contains the top quarter (top 25%) of candidates. Below is a new chart. For comparison, the results of the previous simulation are added.
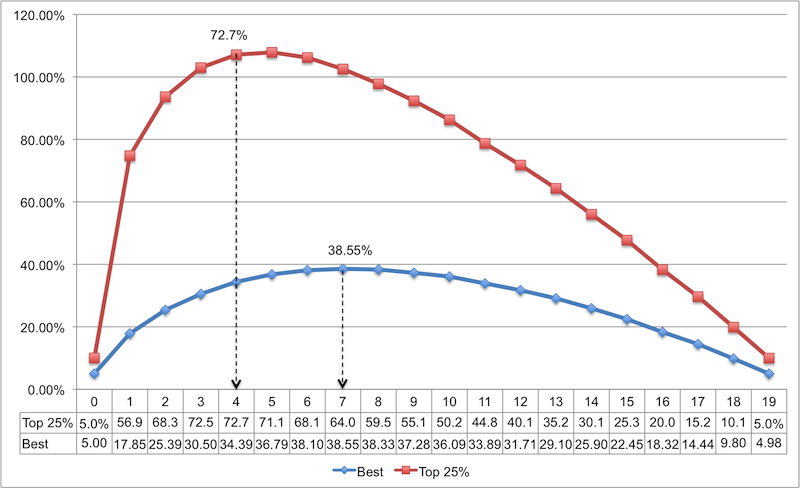
Now the result is encouraging, the most optimal size of the sample list is 4 (although for practical purposes and 3 is quite good, since the difference between 3 and 4 is small). In this case, the probability of choosing a candidate from the top quarter of the list rushes to 72.7%. Sumptuously!
Now let's deal with 20 candidates. How about a list with a lot of candidates? How does this strategy sustain, say, a list of 100 candidates?
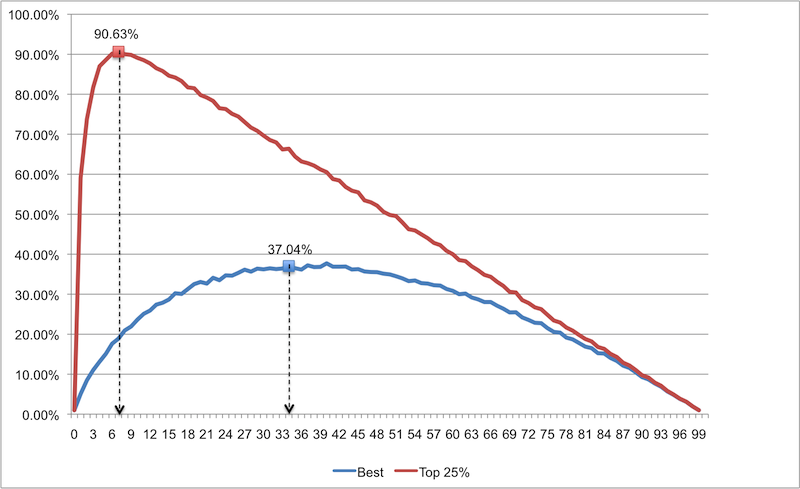
As you can see, this strategy is not suitable for determining the best candidate from a large list (the sample list is too large, and the probability of success is too low). This result is worse than what we obtained for the list with a smaller number. However, if we are satisfied with the candidate from the top quarter of the list (ie, we will be less demanding), 7 candidates in the sample list are enough for us, while the probability of achieving the required results will be 90.63%. These are amazing odds!
This means that if you are a hiring manager with hundreds of candidates, you do not need to try to kill yourself by interviewing everyone. Just interview the sample list of 7 candidates, select the best, and then interview the others one by one until you find one that is better than the best in the sample list. The likelihood that you select one of the top 25% of the list of 100 candidates will be 90.63% (and this will probably be who you need)!
“Musical chairs” (children's play; children go to music around the row of chairs; when the music stops, the players rush to hold chairs, which are one less than the playing ones)
Needless to say, this is the cause of certain difficulties with hiring. It is gratifying that there are many candidates. However, the flip side of this fact is the problem of maintaining a highly qualified engineer with an adequate mindset within the framework of a growing start-up. At the same time, the selection and approval of the candidate must be quick, as the delay, even with a partially suitable candidate, is fraught with its loss within one or two days.
It makes me wonder - which way is better to go if you have a large list of candidates and, in the end, choose the best engineer or, in any case, who is among the best of this list.
')
In the book “ Why Flip a Coin: The Art and Science of Good Decisions ,” HW Lewis wrote about a similar (albeit more stringent) problem with acquaintance. Instead of selecting candidates, the book talks about choosing a wife, and instead of conducting an interview, the problem of dating is considered. However, unlike the book, where it is assumed that you can only meet with one person at a time, in my situation, I obviously can interview more than one candidate. However, the problems that arise are largely unchanged, if I interview too many candidates and spend too much time making decisions, they will be intercepted by other companies. Not to mention the fact that I will probably die before my death from an overdose of intercourse.
In the book, Lewis proposed the following strategy - let's say we choose from a list of 20 candidates. Instead of interviewing everyone, we randomly select and interview 4 candidates and select the best from this sample list. Now, having this best of these 4 candidates in stock, we interview the rest of the list one by one until we meet someone better and, as a result, we hire this candidate.
As you guessed, this strategy is probabilistic and does not guarantee the selection of the best candidate. In fact, there are 2 worst case scenarios. First, if we randomly selected the 4th worst candidates as a sample list and the first candidate selected from the rest of the list is the 5th worst one, then we will hire the 5th worst candidate. Not good. Conversely, if the best candidate is on the sample list, then we risk holding 20 interviews and then losing this best candidate, since the whole process took too much time. Bad again.
So is this a good strategy? In addition, what is the optimal size of the list (total number of candidates) and sample list we need in order to get the most out of this strategy? Let's be good engineers and use the Monte Carlo simulation to find the answer.
Let's start with the strength of the list of 20 candidates, and then sort out the sample list from 0 to 19. For each sample list, we find the probability that the candidate we choose is the best candidate on the list. In fact, we already know this probability, if the sample list is 0 or 19. If the sample list is 0, the first candidate we interview will be selected (since there is no one to compare), so the probability is 1/20, and is 5%. Similarly, with the sample list equal to 19, we will have to choose the last candidate and the probability of this is also equal to 1/20 and is 5%.
Here is a ruby code that simulates this. Run the simulation 100,000 times to calculate the probability as accurately as possible, and save the result in the CSV file optimal.csv
require 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end endrequire 'rubygems' require 'faster_csv' population_size = 20 sample_size = 0.. population_size - 1 iteration_size = 100000 FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv | sample_size. each do | size | is_best_choice_count = 0 iteration_size. times do # population = ( 0.. population_size - 1 ) . to_a . sort_by { rand } # - sample = population. slice ( 0.. size - 1 ) rest_of_population = population [ size.. population_size - 1 ] # -? best_sample = sample. sort . last # best_next = rest_of_population. find { | i | i > best_sample } best_population = population. sort . last # ? is_best_choice_count + = 1 if best_next == best_population end best_probability = is_best_choice_count. to_f / iteration_size. to_f csv << [ size, best_probability ] end end
The code is quite self-evident (especially with all the comments), so I will not go into details. The result is shown below in a linear graph, after opening and marking the file in MS Excel. As you can see, if you select 4 candidates as a sample list, you will have about 1 chance out of 3 that you choose the best candidate. The best odds are if you select 7 candidates as a sample list. In this case, the probability that you choose the best candidate is about 38.5%. It doesn't look very good.

But, to be honest, in the case of several candidates I do not need that the candidate be “the best” (in any case, such assessments are subjective). Suppose I want to get a candidate in the top quarter of the list (top 25%). What are my chances then?
Here is the revised code that models it.
- require 'rubygems'
- require 'faster_csv'
- population_size = 20
- sample_size = 0 .. population_size - 1
- iteration_size = 100000
- top = ( population_size - 5 ) .. ( population_size - 1 )
- FasterCSV. open ( 'optimal.csv' , 'w' ) do | csv |
- sample_size. each do | size |
- is_best_choice_count = 0
- is_top_choice_count = 0
- iteration_size. times do
- population = ( 0 .. population_size - 1 ) . to_a . sort_by { rand }
- sample = population. slice ( 0 .. size - 1 )
- rest_of_population = population [ size .. population_size - 1 ]
- best_sample = sample. sort . last
- best_next = rest_of_population. find { | i | i > best_sample }
- best_population = population. sort . last
- top_population = population. sort [ top ]
- is_best_choice_count + = 1 if best_next == best_population
- is_top_choice_count + = 1 if top_population. include ? best_next
- end
- best_probability = is_best_choice_count. to_f / iteration_size. to_f
- top_probability = is_top_choice_count. to_f / iteration_size. to_f
- csv << [ size, best_probability, top_probability ]
- end
- end
In the Optimal.csv file, we added a new column, which contains the top quarter (top 25%) of candidates. Below is a new chart. For comparison, the results of the previous simulation are added.

Now the result is encouraging, the most optimal size of the sample list is 4 (although for practical purposes and 3 is quite good, since the difference between 3 and 4 is small). In this case, the probability of choosing a candidate from the top quarter of the list rushes to 72.7%. Sumptuously!
Now let's deal with 20 candidates. How about a list with a lot of candidates? How does this strategy sustain, say, a list of 100 candidates?

As you can see, this strategy is not suitable for determining the best candidate from a large list (the sample list is too large, and the probability of success is too low). This result is worse than what we obtained for the list with a smaller number. However, if we are satisfied with the candidate from the top quarter of the list (ie, we will be less demanding), 7 candidates in the sample list are enough for us, while the probability of achieving the required results will be 90.63%. These are amazing odds!
This means that if you are a hiring manager with hundreds of candidates, you do not need to try to kill yourself by interviewing everyone. Just interview the sample list of 7 candidates, select the best, and then interview the others one by one until you find one that is better than the best in the sample list. The likelihood that you select one of the top 25% of the list of 100 candidates will be 90.63% (and this will probably be who you need)!
Source: https://habr.com/ru/post/285334/
All Articles