Mathematical model of perception (Part 3)

Part 1
Part 2
Foreword
History knows examples when discoveries were given to humanity by chance: it learned about clay, gunpowder, and rubber, but hardly anyone could discover a silicon transistor or polyethylene by accident. The architect, designing the bridge, to be sure of the reliability of the constructed structure, must have a good understanding of the properties of mechanical stresses. If you suddenly think about how to create an algorithm that allows the machine to independently navigate in the forest more often or without any help to study new subjects for it, the contents of the next chapter, devoted to the concepts "subject" and "place", may be useful for you. It is possible to read it without large losses independently of the previous chapters; the introduction to part 1 will help clarify some details.

Escher: man with cuboid

Items and places

Perhaps one of the simplest examples of the subject is a playing card with a symmetrical shirt. What is it for our thinking? Certainly not a “picture” (color configuration) in the standard position: turning, the map remains a map, while the picture changes. In addition, the map can be flipped over in any position. upside down. Below, the figure shows the connection between changing the ways to see the map and possible actions on it, where ↷ denotes a 90 ° rotation and means turning the card face-down.

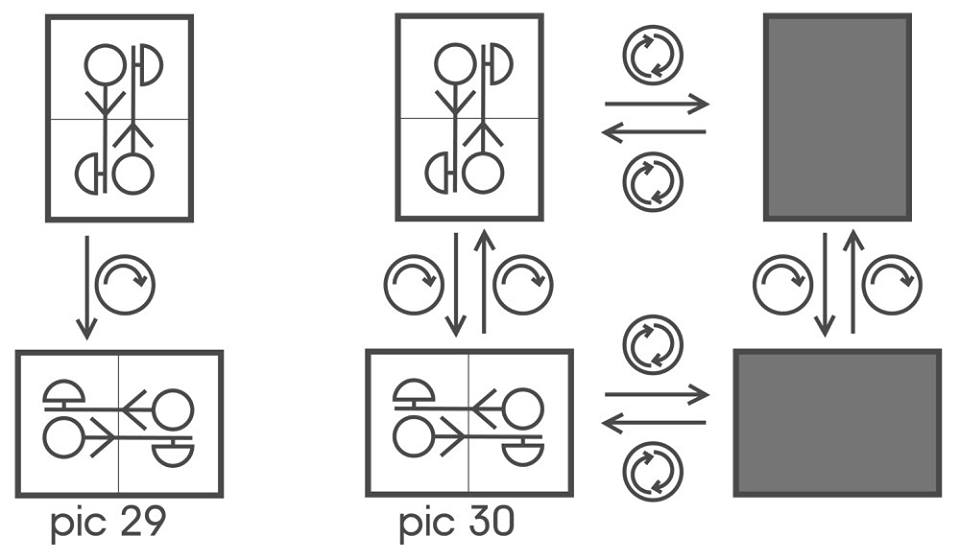
The following example, which we consider, is a point in the "field of view" of the probe. We fix some hexagon in the lattice region, which is currently viewed by the probe. Without loss of generality, its color can be considered black. If then we perform various elementary displacements, but so that this hexagon remains in the “field of view” all the time, then a pattern will be established between the types of allowable movements and the change of color configurations, schematically shown in Fig. 31

For these two examples, it is characteristic that the object (or place) turns out to be a set of “pictures” along with a set of allowed actions defined for each “picture”. So, an empty transparent glass standing on a table can be turned in front of you as much as you want, while some positions of the glass's vision will be turned into others by turns, and the glass will still remain itself. In contrast to turning, to drop a glass on a hard floor is not an allowed action from any vision position.
Some objects, nevertheless, like a playing card, cannot be defined as a “point” and a glass. Apparently, one of the most ideologically complex objects is a cube with faces painted in different colors (Figure 32).

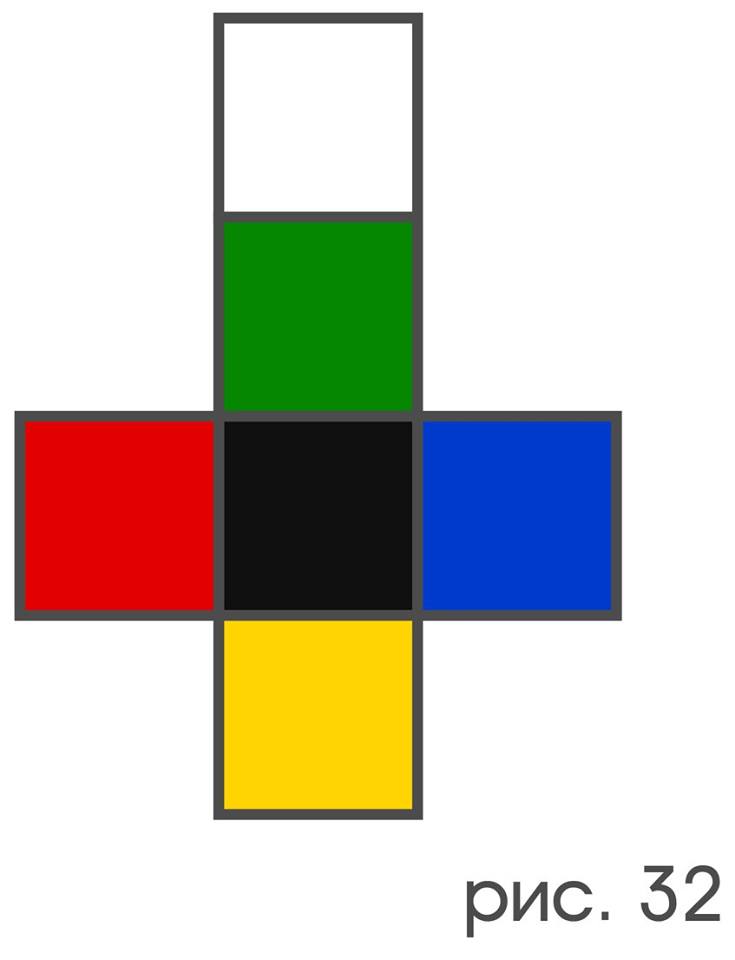
We will also assume that this cube is located relative to three axes: vertical, longitudinal and transverse, and the view is always directed along the longitudinal axis (Fig. 33). The observer is allowed to rotate the cube 90 ° at a time around any of these axes in any direction, but at the moment of rotation he must close his eyes, so that the cube for him, in fact, has many observed colors varying from certain actions.

However, the relationship between actions and changing colors turns out to be somewhat more complicated than in the case of map positions and a black dot: when the map is face down, the only position she could take after turning is face up, face down, on the other hand, the observer sees the black face of the cube, only this does not determine the color of the face that will become visible after turning "on itself".
A common technique that often allows such experiments to return uniqueness to such experiments is to remember all the time the sequence of recent actions and colors. For example, in the case when the observed face turned out to be black after being turned green to the left, and no actions have been taken since then, the turn on itself has been performed under these conditions to make it change its color to blue. But in general, even if you remember the sequence of millions of recent actions and colors, whether all these colors are black and the actions rotate around the longitudinal axis, the memory of this in itself will not give any chance to predict which side the cube will appear to you after turning on "on myself".
Apparently, it is impossible to give a satisfactory definition of the concept of “subject”, including the case of a cube, unless it is well understood the subtleties of the process of perception. To do this, following the general logic of presentation, imagine a bouquet of three lamps. It is convenient to depict the joint history of changes in their states by a chronogram (Fig. 34), on which the line running from each lamp is a copy of the time axis, and the bold areas on it are the periods when the lamp was burning.

In relation to time 4 on the above chronogram it can be said that

 1  ;  2 ;  3  . 

In relation to time 1:

   1 ;  2 ;  3 . 

“Lit”, “not lit”, “extinguished” or “light up” a specific lamp - these are properties of moments of time, which are always set precisely by direct observation. It may happen that the manifestation of such directly observable properties is subject to certain laws. For example, a careful study of the chronogram (moments 1,1 ', 1' ') leads to the observation:
I. whenever lamp 1 is on, lamp 2 is extinguished, lamp 3 lights up;
Ii. lamp 3 lights up only at those times when lamp 2 was extinguished while lamp 1 continued to burn.
If such statements about directly observable properties are considered to relate exclusively to the history of the past, then each of them is either proved or refuted by this history. On the other hand, the observed patterns are often assumed to be true both in relation to future observations and in relation to the past in the conditional mood: for example, every person living in middle latitudes is sure that the Sun will rise again tomorrow morning, and some biologists say that if there were no glaciations of the Earth, then dinosaurs would live in our days. No matter how reasonable the last two assumptions may seem, it is impossible to prove them: all of them are merely hypotheses, since not one regularity that has been fulfilled in the past can be maintained at all in the future, and even more so in the case of an alternative development of history. Such a state of affairs, however, is not a reason to reject the use of hypotheses in our practical activities; rather, we just need to change our attitude towards errors: they are not something negative, but only an integral part of cognitive activity.
Taking into account the comments made, we slightly reformulate (i) and ii):
I. whenever lamp 1 is on (if it were on), and lamp 2 goes out (if it goes off), lamp 3 lights up (lights up);
Ii . The lamp 3 can (could) light up only in those moments when the lamp 1 is on (on) and the lamp 2 goes out (on).
The new meaning of the concept “regularity”, in which it appears to be applied both to the future and to the alternative course of chronology development, allows us to single out another kind of properties of moments of time: properties observed as hypotheses (hypothetically-observed properties). For example, the property “if the lamp 2 would go out, then at that moment the lamp 3 would light up” appears (observable) at moments 1,1 ', 1' 'and is true for all moments as a hypothesis in which lamp 1 was burning if only the hypothesis I * is true.
Pontiya properties and patterns allow us to clarify what was the map and the black dot. To see a picture in a certain position or a certain receptor to perceive black color is a property that can be directly observed. Thus, both the map and the black dot are a system of directly observable properties and actions, interconnected by laws of the form "whenever property A is fulfilled and action B occurs, property C” follows after this.
Let us now try to understand what a cube is. Observing the movements and color changes of the observed face caused by them for quite a long time, you can see that whenever yellow turns to "black", the next movement changes color:
a) Black to blue if it is turning “left”;
b) Black to red if it is turning “right”;
c) Black to green, if it is turning on itself;
d) Black to yellow, if it is a turn "from itself";
e) Black to black if it is a turn around the longitudinal axis.
Pattern a: “the next movement, if it is turning“ left ”, black changes to blue” turns out to be true not only in the described situation: it is not disturbed even, for example, every time after turning red “left” it changes to black , moreover, at the same time the rest of the laws are true. All these patterns are just hypotheses, but nevertheless, through sufficiently long observations, another pattern-hypothesis is found: if the need to be true to one of the ad patterns is suddenly established, then all the other ae are true.
The property-hypothesis, which is the conjunction a ⋀ b⋀ c⋀ ​​d⋀ e, for the property will be denoted by a graphic symbol:

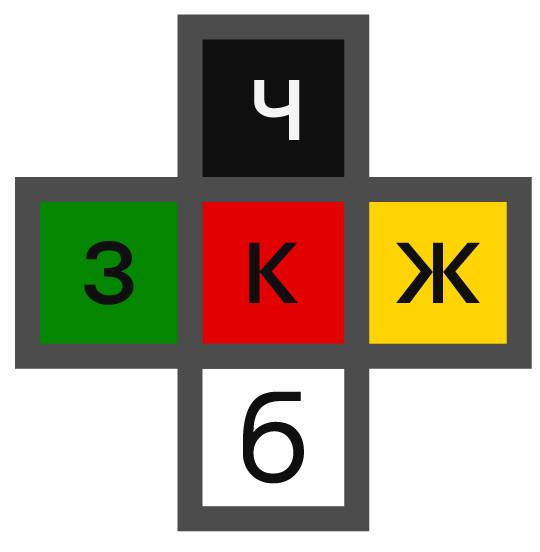
It is not difficult to guess that for some moment it is equivalent to establish the fulfillment of the property that it is possible to assert that at this moment the cube, as a geometric body, faces the observer with a black face, while the reverse side is white, the top is green, the bottom is yellow, the left is red, and right blue
If, instead of the property: “yellow when turning“ on itself ”changes to black” as the starting point of the reasoning, take: “green when turning“ to the right ”changes to red”, then in the end we will come to the property

and taking: "blue when turning" from itself "changes to black" - to the property:

These properties are referred to as orientation properties. In whatever position, like a geometric body, there is a cube, for each movement, whether it is “on itself”, “from itself”, “left”, “right” or a turn around the longitudinal axis, we can call the rule setting position it will be after performing a specific movement. The reader may notice that each orientation of the cube uniquely corresponds to a certain orientation property, thus, the orientation properties and the movements produced turn out to be subject to exactly the same rules. For example, through fairly long observations, the following patterns are detectable:

• whenever it can be argued (as a hypothesis) the validity of the property
  
  

  and the next movement is a “counterclockwise” rotation around the longitudinal axis, then, following its execution up to the next movement, the property
  
  

  ** whenever it is possible to assert the validity of the property
  
  

  and the next movement is a turn "from oneself", then after its execution right up to the next movement
  
  

  All patterns between orientation properties in which
  
  

  schematically depicted in figure 35.
  
  

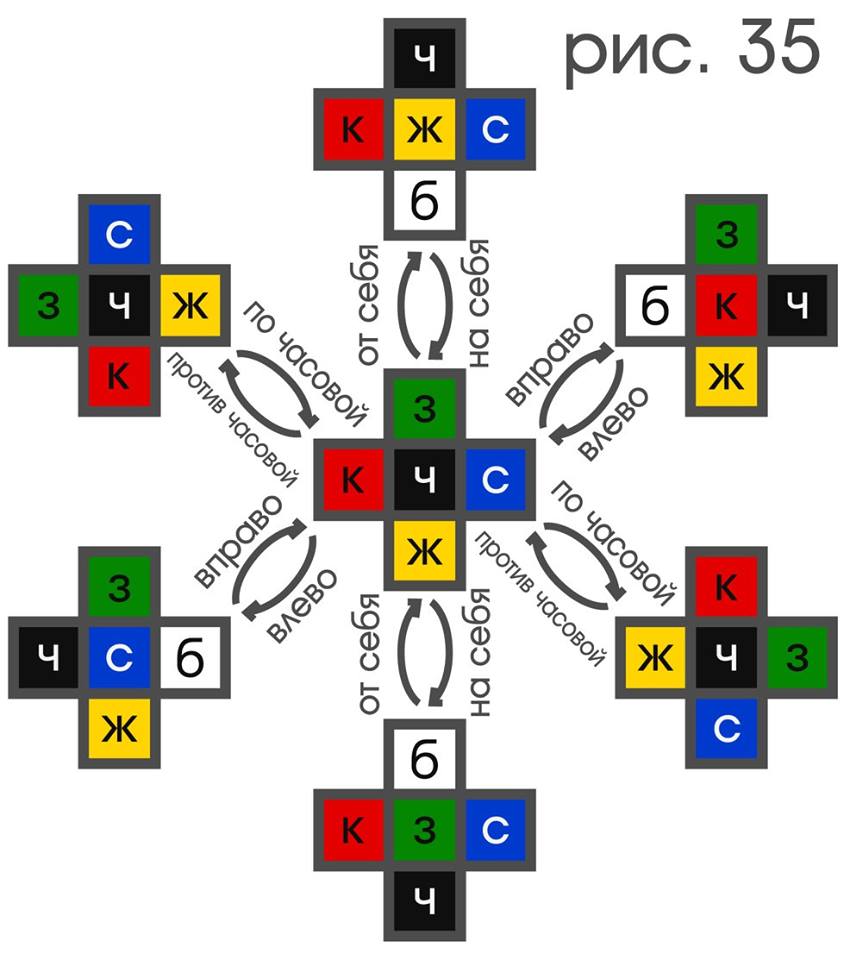
  Adding the scheme in the last figure with the other orientation properties (there are only 24 of them in the cube), as well as the rules between their shift and the movements performed, we get nothing more than what the colored cube is for the observer’s thinking in the described experiment. In this form, the definition of a “cube” is similar to the definition of a “map” and “a point”, with one exception: instead of directly observable properties, it includes the properties observed hypothetically.

  
  
  
  

  Sergey Kovalenko
  Dubna 2015-2016

  
  

  Initially, only three parts were intended, but the last chapter, “The Role of Language in the Mechanisms of Forming Essentially New Concepts,” trying to be simply and clearly written, eventually gained too much volume. I hope to publish it in about a couple of weeks.