When shooting a book spread with the help of a camera of a mobile device, inevitably some of the following defects appear (and maybe all at once):



• digital noise,

• shadows and highlights,

• defocusing and lubrication,

• skew

• perspective distortion,

• curved lines

• extra objects in the frame.



Processing such photos for the subsequent OCR is a rather laborious task, even for a person who is well versed in Photoshop skills. What if we want to do this automatically using the program? Immediately make a reservation that a detailed description of all stages of the algorithm would make the publication too voluminous, so we will now tell only how to solve one of the subtasks - to find the spine line in such photos. We already told about how to eliminate shadows and glares in photos. Many articles have been written about eliminating digital noise. And about the automatic correction of perspectives and curved rows, we will tell you next time.

')

At first glance, the task is not difficult: we select all the contours in the image using one of the gradient operators (for example, Sobel) and look for the strongest and longest of them using the Hough transform:











We need to find the brightest pixel in the picture on the right and get the equation of the line from its coordinates. And it's all? Someone may decide that you can still reduce the image first so as not to do all this in an image of 5-10 megapixels. But something suggests that it will not always work so easily. Consider the possible situations:



The spine has no shadow:







On the page there is a photo with a dark frame:







Or just a big dark photo:







Table:







Multicolumn text with separators:







In such situations, the trivial algorithm given above will err too often. Let's try to improve it a little and take into account the examples given.

Pre-processing to emphasize a weak shadow at the spine

We convert the image into a halftone (gray) and apply the UnsharpMask filter with the following parameters: radius = 41, strength = 300.

Quickly determine the orientation of text lines

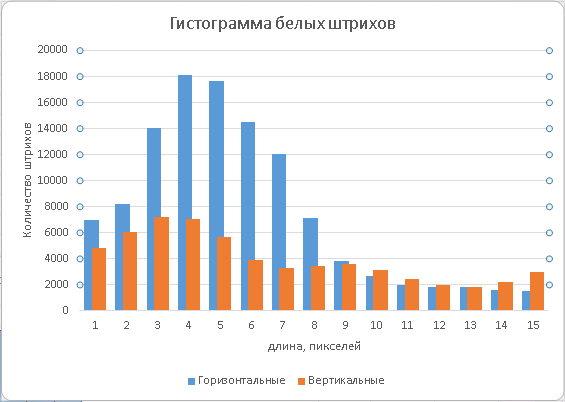
To determine in which direction we should cut the image, we look for the direction of the lines of text. This can be done on the binarized image from the histograms of the lengths of the white RLE-strokes. It is known that the distance between lines is usually greater than the spacing between letters in a multi-line text (otherwise it would be difficult to read). The bar length length histogram should be collected over the area of ​​the image containing the text. You can use the simplest classifier of text blocks or simply retreat from the edges of the image by 10-15% so that the fields and the background do not “obscure” the collected statistics. Denote the sum of the areas of horizontal white strokes having a length not exceeding a certain threshold L, as S _h , and the sum of the areas of vertical strokes as S _v . Then, by changing the threshold L, we can follow the ratio max (S _h , S _v ) / min (S _h , S _v ), and as soon as it becomes greater than 2, we can say with confidence that we have found the letter spacing. And at the same time they determined the direction of the lines: if max (S _h , S _v ) = S _h , it is horizontal, otherwise it is vertical. We took the ratio equal to 2, so as not to make too many gaps in the definition of orientation and at the same time, not to be mistaken too often. By changing this value, you can get different points on the precision / recall graph. You can use additional features from the same histograms. In cases where we fail to determine the orientation in a uniquely simple way, we launch a search for a strong root (shadow) hypothesis in both directions (horizontal and vertical) and evaluate the direction of the text lines as perpendicular to the direction of the root, which has a stronger response.

Strong hypothesis (shadow)

Suppose there is a shadow in the photograph in the spine. Prepare an image to search for this line:



a) reduce the image to a specified size, for example, to 800 pixels on the long side;

b) we get rid of large shadows with the help of the morphological operation TopHat: we subtract its opening from the original image, i.e. build-up from erosion (r = 5), by signal = 1 we mean black, and white background = 0;

c) we remove the lines (short vertical black strokes) with the help of vertical erosion (r = 3);

d) after receiving the image of the lines as the difference between the two previous results, we use it as a penalty, adding to the current one.



a)



b)



c)



d)



We apply the fast Hough transform to the last image and look for the global maximum in the inverted image:







You can take into account the statistical distribution of the angle from the vertical and horizontal displacement of the spine line. As a rule, in 99.9% of cases the angle does not exceed 20–25 degrees in absolute value, and the middle of the spine line has a coordinate from w / 3 to 2w / 3 (w is the image width). In this case, the extreme values ​​of angles and coordinates are much less likely than the average. It is possible to take into account this distribution in the values ​​of points in the Hough space, imposing a penalty for deviation from the most likely position in the angle and coordinate (0, w / 2).



If the found global maximum exceeds the threshold for the detection of a strong hypothesis, we assume that we have found the line of the root along the shadow. In this case, we transform the coordinates of the maximum into the equation of the line. We select the threshold value experimentally on a large sample of photos, minimizing the number of errors and omissions.

Weak hypothesis (lumen)

With a selected threshold value, in about 10% of cases, a strong hypothesis does not find a solution. As we know, the shadow may be absent in the spine. This can happen with a strong reversal of the turn or if a flash was used when shooting. Let's try to find the line of the spine in the central lumen.



We calculate the gradient modulus (b) on a reduced half-tone image (a) (Sobel operator):



a)



b)



Here another example was specially chosen, since the presence of a strong shadow will interfere with this algorithm.



On the binarized image c) we glue the text into blocks using the morphological operation of dilation (d, r = 6 for an image of 800 pixels). Apply the resulting mask of text areas to the image of the modulus of the gradient (e, the signal was amplified 4 times).



c)



d)



e)



Now, smooth the mask of text areas (d) with Gaussian blur (f) (r = 8) and add to it the resulting enhanced gradient of non-text areas (g).



f)



g)



Now we have an image where the spine line, if it contains at least a weak gradient, gives an additional contribution to the signal of the lumen region. If there is no gradient, i.e. If there is no visible line in the image, we will select a line that is sufficiently distant from the text on both sides due to Gaussian blur. With a narrow spine, it will be approximately in the middle.



To search for the line, we will again apply the Hough transform, and look for the global maximum, taking into account the statistical distribution of the angle and offset:







The coordinates of the maximum transform into the equation of the line of the spine. Done!



This simple algorithm on the basis of> 1800 photos of book spreads available in our database gives less than 1.5% errors.



Of course, there are many opportunities to improve it: you can select additional features in the image, calculate not two hypotheses sequentially, but several at once, evaluate their mutual arrangement, select objects in the image (lines, separators) and analyze them ... the moment there will be a need to once again expand the training (and test!) sample in order to avoid possible retraining. All this is an endless struggle for the quality of the algorithm.



Solving the problem of finding the line of the spine, we forgot to say, but why do we even need it? Why do I need to look for this line in the photo? Very simple: the spine line allows you to eliminate the skew, i.e. rotate the image so that this line becomes vertical, it divides the image into two pages for the subsequent application of the row extension algorithm, it helps to identify perspective distortions (although it will need to find more perspective vanishing points). In general, without solving this problem, it is hardly possible to prepare such photographs for the subsequent OCR. These algorithms have already found their use in the BookScan technology, which is part of our mobile application ABBYY FineScanner .