Using Matalysis in computer games (part 3)
Keywords: DPS (DamagePerSecond); Wolfram Mathematica; discreteness and continuity; mathematical analysis; earnings game currency in computer games; packs ArcheAge.
Everyone is familiar with the same type of questions in school math problems about a motorcyclist leaving point A to point B, which cause boredom, disgust, or simply indifference. Questions that cause, anything except interest in the study of mathematics. Obviously, much more interest and more emotion raise questions like:
1) "How could he defeat me in the game, if my character has more health and DPS (Damage Per Second) is higher ?!"
2) "How fast to earn gold (game currency) to make your character stronger?"
In fact, these game questions are very similar to the classic school tasks. The only difference is that there is an interest in getting an answer to the game questions, there is a goal for which I want to solve these problems. Unfortunately, many teachers in schools and universities do not know how to interest students in obtaining specific information, a new method for solving mathematical problems, and bringing them to answer. But since the games cause this very interest, it is a sin not to use the interest in the game, to awaken interest in mathematical analysis.
Here are two tasks that are only reformulated by the above questions.
1) Petya and Kolya decided to help grandfather fill two identical empty barrels with water from a well. Petya dragged water in a 5-liter bucket and spent 3 minutes on one call to the well and back to the barrel, and Kohl on the 8-liter bottle and spent 5 minutes on one call. Each filled his own barrel. Which of the boys will fill their barrel faster if a) the volume of the barrel is 60 liters? b) if the volume of the barrel is 56 liters? (boys started at the same time)
2) Two merchants Semyon and Dobrynya buy from the peasants 10 pounds of honey for 5 gold and take it for sale to neighboring cities. Dobrynya is taking him to the nearest city and selling it there for 8 gold, all the way to the city and back it takes 2 days. Semen, who wants to sell his honey as much as possible, is not lazy and takes him even further, spending 3 days all the way, and selling honey in another city for 10 gold. Which of the merchants will earn more in 360 days of continuous work? How will the situation change if both merchants force the peasants to lower the price of honey to 3 gold?
The analysis of these tasks, described below, will help answer the burning questions of the game ArcheAge (and others) about "packs" and DPS. And also allows you to reflect on such concepts as "discreteness" and "continuity", as well as on such a seemingly obvious question as "profit".
In order to make it easier to deal with the task of the barrel, it is very convenient to draw everything that happens on the graph. Let 's mark Petya in red and Kohl in green. We get two ladders. Kohli’s barrel and Petit’s barrel are filled in discretely, the length of the steps is equal to the hike to the well and back to the barrel, and the height is equal to the amount of water brought in liters. On most of the resulting graphics, the red ladder is above green, but in some areas it is above green.

To fill a barrel with a volume of 60 liters, using a 5 liter bucket, you need to run 12 times with this bucket to the well. As a result, Peter will spend 3 minutes * 12 times = 36 minutes. Kolya, with his 8 liter bucket, needs 60/8 = 7.5 times. We get a non-integer number. For 7 campaigns, Kolya will bring only 7 * 8 = 56 liters, which is less than necessary. And if Kolya goes for water again, he will bring 64 liters already, which is even more than necessary. As a result, Kolya will need 8 times * 5 minutes = 40 minutes, that is, Petya used to fill his barrel.
The situation changes if it was necessary to bring 56 liters. For this, Kolya needs to run 56/8 = 7 times, and it takes 35 minutes. Petya will need 56/5 = 11.2 times, but since it is an integer that is important, in fact, Petya will need to go 12 times and it will take 12 * 3 = 36 minutes. In this case, Peter will fill his barrel later Kohl.
It turns out that such a strange situation is that the answer to the question of who will fill the barrel faster depends not only on the boys, but also on the size of the barrel. And if you look at the graph, then the places where the graphs intersect quite a lot. Moreover, you can even make Petit's barrel 55.9 liters, that is, less than Kolya’s, and he will fill it anyway later. This fact becomes even more surprising if we calculate the average filling rate of the barrel for Petya and Kolya. In Petit, the average speed is 5/3 = 1.666 liters / minute, and in Kolya 8/5 = 1.600 liters / minute. Kohl may even start half a minute later, and still Petya will be second.
That is, Petya has a faster filling rate and a smaller barrel, and he began earlier, but he will fill his barrel anyway later than Kolya will fill his own.
Such a paradoxical result is obtained precisely because the process of filling the barrel is discrete.
If we consider the case when two opponents in the game hit each other with different strengths and different speeds, then this situation will be similar to barrels and buckets, which we have already considered. And as was shown above, it is not always worth relying on the so-called DPS, that is, on the average damage rate, in assessing the strength of you and your opponent.
Is DPS not applicable at all? Not really. In some cases, it adequately describes the situation.
For each ladder, you can build two parallel lines that will pass through the upper corner points and through the lower ones.
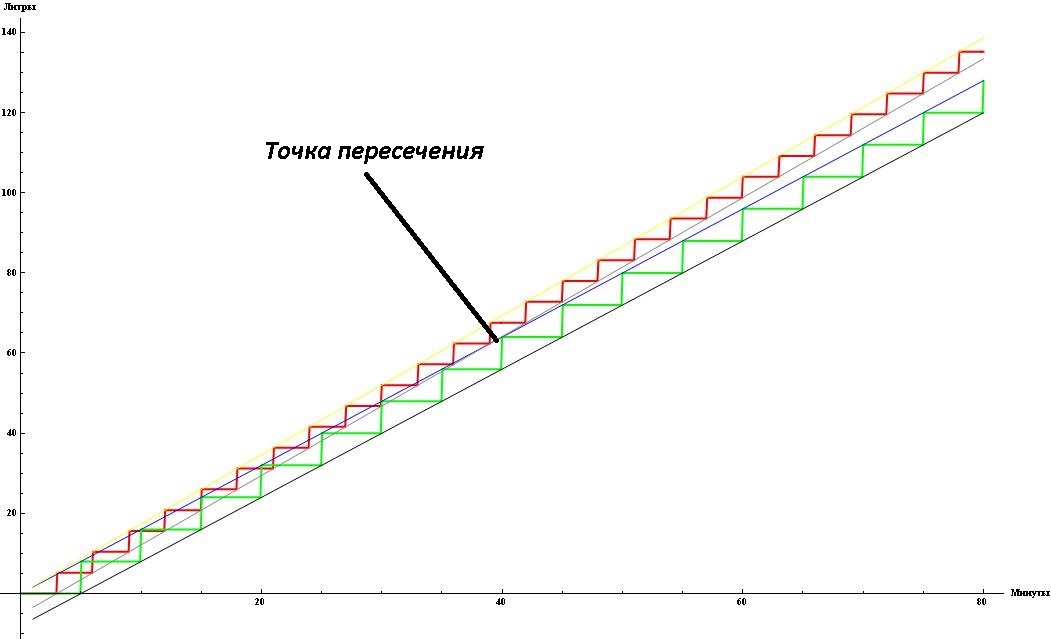
That staircase, which has a higher DPS, after some point will always be higher than the second. And this moment can be found as the intersection of the lower straight ladder of the larger DPS, from the upper straight ladder of the smaller DPS. Here are the formulas for these two straight lines.
fDPSL1 (t) = (DPH1 / Period1) * (t-Period1);
fDPSH2 (t) = (DPH2 / Period2) * t;
DPH1 and DPH2 is the impact force (bucket volume) for the period Period1 and Period2, respectively. DPH1 / Period1 = DPS1. And the intersection of these lines occurs at the moment
T = Period1 / (1-DPS2 / DPS1)
From this formula it is clear that the influence of the discreteness of the situation, and the possibility of the emergence of paradoxes associated with the discreteness, depends on two factors. The first factor is the approximate equality of the DPS of both opponents. In this case, the denominator vanishes, and the time of the termination of the influence of the discreteness of the situation tends to infinity. The second factor is the period of strikes of the person who has a higher DPS. The higher the frequency of strikes, the shorter the period, and hence the time for the termination of the influence of discreteness will be less.
More from the formula for the top straight
fDPSH2 (t) = (DPH2 / Period2) * t
it can be seen that this is just a formula for damage to time with a fixed DPS.
fDPSH2 (t) = DPS2 * t
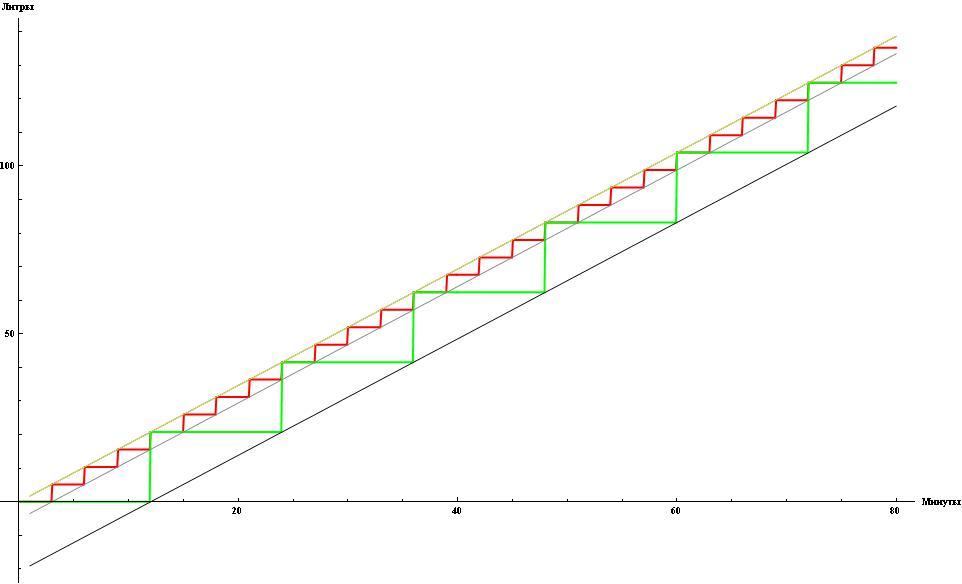
If the opponents of the DPS are the same, then the one with LESS and the strength and period of the blows will be in the best position. In the limiting case, if the period of strikes tends to zero, then the ladder will turn into a “continuous” straight line of the form fDPSH (t) = DPS * t. And this line is the most profitable option with a fixed PDS.
Thus, if there is a choice to increase the strike force by N% or increase the strike frequency by the same N%, then it is more profitable to increase the frequency, although in both these cases the DPS will increase equally. However, as practice shows, many, due to some intuitive delusions, prefer to increase the impact force.
')
The problem of merchants is solved in a similar way. Semen spends 5 gold for one trip, gets 10, for a total profit of 5 gold for 3 days. Dobrynya for 2 days gets 3 gold. In 360 days, Simon will make 120 trips and earn 600gold. Dobrynya will earn 360/2 * 3 = 540 gold. As a result, Simon does the right thing, that he carries on, he will earn more than Dobryni. If Simon and Dobrynya agree, and find a way to force the peasants to sell them 3 gold each. Then, in one trip, Simon will receive 7 gold, and Dobrynya 5. For 360 days, Simon will receive 360/3 * 7 = 840, and Dobrynya 360/2 * 5 = 900. That is, Dobrynya will earn more Seeds in 360 days, despite the fact that it will sell its goods cheaper.
In economics, there is such a thing as profitability - the ratio of sales profits to the cost of goods sold.
So, if we consider the ratio of profit to cost, then Seeds profitability may seem higher. In one trip, spending 5 gold, he gets 5gold profits. Dobrynya, for 5 gold, receives only 3 gold profits. But with this approach, as you can see, time is not taken into account at all, and it is necessary to insert it in the cost price as the salary of Semen and Dobryni for transportation. That is, in addition to the money that they invest, you need to take into account the time that they spend. And when it comes to making a profit, about the method of earning, then it is necessary to take into account not only the profit obtained as a result of some actions, but also the time spent on them.
In order to make it clearer, how does it happen that selling at a lower price can be profitable, once again draw a chart. The graph shows the dependence of the profits per unit of time from the cost of goods for 3 different cases. In each case, the product and its cost will be considered the same, but the sale price and time for transportation will be different. Graphs are constructed using a simple formula.
F [Cost Price] = (Selling Price - Cost Price) / Transportation Time
Examples of time and sale prices are taken from the game ArcheAge. Time is measured in minutes, and prices are in gold.
In the first case, Sale Price = 8g, Time = 6 minutes, in the second Sale Price = 11g, Time = 10 minutes, and in the third case Sale Price = 13g, Time = 16 minutes
In the network you can find a table of prices for the sale of all possible goods in the game ArcheAge, for example, here
But, nevertheless, in these tables the distances to points of sale are not indicated, which of course is a big disadvantage.
The real costs of raw materials, which are necessary for the manufacture of goods, in the game vary greatly, due to fluctuations in the gaming market. Prices, generally speaking, are set by players, including the so-called "work points", which are necessary for the production of goods, and which can also be bought on the "market". The cost in this example is approximately 7g, but it can be much more expensive.
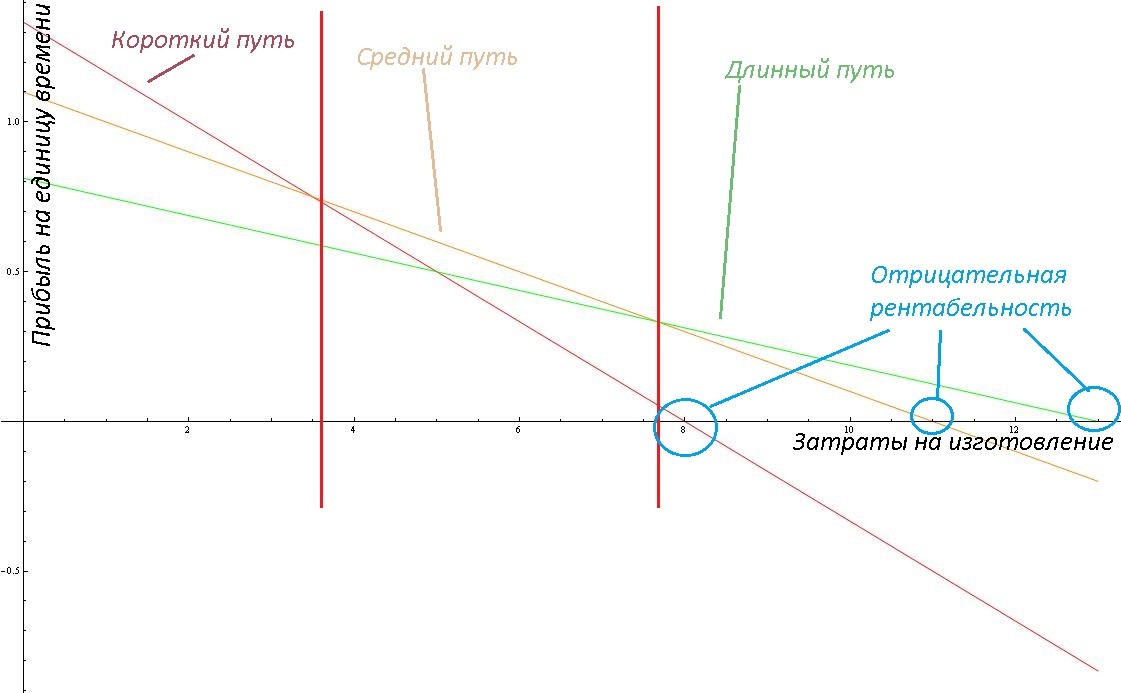
Understanding some of the tasks, the process, very often helps to consider extreme cases. If the cost of goods is zero, then all the profit per unit of time is determined by the time that will be spent on transportation. In the general case, all 3 straight lines may not intersect, but in this particular case, at low cost, it is more profitable to carry to the nearest point of sale. If the cost is high, then it may be higher than the selling price at the nearest points, which means that you will work with negative profitability, that is, spend more than you get. And then the only opportunity to earn at least some will be selling in the most remote place, where the selling price is higher than the cost price. But at too high cost, even selling there is not profitable. There is also an intermediate option, when it is most advantageous to carry the average distance.
It is worth noting that the effects associated with the "discreteness" of making a profit are also naturally present here. The principle of analysis of these effects is similar to that discussed above.
When you try to tell such players, you often get in response “Lol ?! I know what to do! What are you teaching me ?! ”. People persist in selling their goods as expensive as possible, and absolutely do not pay attention to how much time they spend on it. Time, however, can be expressed in currency and use this “price of time” in the cost price, and then everything becomes much clearer. But very often there are those who, for the sake of 1 gold, are ready to drive even further, wasting time with much less efficiency. In the end, having been greedy, they lose more.
And what is most interesting, even those who know about these subtleties, very often succumb to the inner momentary temptation, blind erroneous intuition, and the insidious and dangerous feeling of greed, and still the rod to where it is not profitable to sell, but where they see that the sale price of their goods is higher. Psychophysiology - even matan sometimes does not work against it. But this particular feature of human perception is loved to be used by all who feel like it, parasitizing on greedy people.
Wolfram Mathematica is an extremely powerful tool for solving various tasks of any complexity. However, one should not think that since Mathematica can do so much, it is extremely difficult to use. In fact, I very often use it simply as a very convenient, but also very advanced calculator. There is no need to write code for algorithms. To draw graphs, or quickly create an interactive window, with input fields, sliders and drawing functions in real time, a few simple commands will suffice, which are described in great detail on the heap of examples in the built-in help.
Here is an example of the code for graphing profit / cost graphs.
And a code sample for such a convenient window for drawing discrete processes. You can change the parameters and immediately compare the results obtained on the graph.

You just need to copy the code into the empty Wolfram Mathematica window and press Shift + Enter. The result you get in the same window.
The Internet is not omniscient. Guides, recipes, manuals for all occasions in it is not found. In each particular case, the refinement, the modernization of well-known methods will allow to achieve the best results. But this requires analyzing the situation, and synthesizing new methods based on known data. But such skills will not arise by themselves, they need to be trained, trained. And sometimes it can be done dull and lazy. There are two ways out: either to try the learning process at school or at a higher education institution, which often seems meaningless and boring, to make it conscious, meaningful and interesting, or, doing something interesting and fascinating, find interesting moments in it, analyze them and try to solve game tasks as complete maths tasks.
If you teach a teacher that is boring and inactive, then this is no reason not to deal with MatAnalysis. In the end, making excuses for a bad teacher, you are more interesting in your life, and you will not make yourself more successful.
Introduction
Everyone is familiar with the same type of questions in school math problems about a motorcyclist leaving point A to point B, which cause boredom, disgust, or simply indifference. Questions that cause, anything except interest in the study of mathematics. Obviously, much more interest and more emotion raise questions like:
1) "How could he defeat me in the game, if my character has more health and DPS (Damage Per Second) is higher ?!"
2) "How fast to earn gold (game currency) to make your character stronger?"
In fact, these game questions are very similar to the classic school tasks. The only difference is that there is an interest in getting an answer to the game questions, there is a goal for which I want to solve these problems. Unfortunately, many teachers in schools and universities do not know how to interest students in obtaining specific information, a new method for solving mathematical problems, and bringing them to answer. But since the games cause this very interest, it is a sin not to use the interest in the game, to awaken interest in mathematical analysis.
Here are two tasks that are only reformulated by the above questions.
1) Petya and Kolya decided to help grandfather fill two identical empty barrels with water from a well. Petya dragged water in a 5-liter bucket and spent 3 minutes on one call to the well and back to the barrel, and Kohl on the 8-liter bottle and spent 5 minutes on one call. Each filled his own barrel. Which of the boys will fill their barrel faster if a) the volume of the barrel is 60 liters? b) if the volume of the barrel is 56 liters? (boys started at the same time)
2) Two merchants Semyon and Dobrynya buy from the peasants 10 pounds of honey for 5 gold and take it for sale to neighboring cities. Dobrynya is taking him to the nearest city and selling it there for 8 gold, all the way to the city and back it takes 2 days. Semen, who wants to sell his honey as much as possible, is not lazy and takes him even further, spending 3 days all the way, and selling honey in another city for 10 gold. Which of the merchants will earn more in 360 days of continuous work? How will the situation change if both merchants force the peasants to lower the price of honey to 3 gold?
The analysis of these tasks, described below, will help answer the burning questions of the game ArcheAge (and others) about "packs" and DPS. And also allows you to reflect on such concepts as "discreteness" and "continuity", as well as on such a seemingly obvious question as "profit".
Paradox DPS
In order to make it easier to deal with the task of the barrel, it is very convenient to draw everything that happens on the graph. Let 's mark Petya in red and Kohl in green. We get two ladders. Kohli’s barrel and Petit’s barrel are filled in discretely, the length of the steps is equal to the hike to the well and back to the barrel, and the height is equal to the amount of water brought in liters. On most of the resulting graphics, the red ladder is above green, but in some areas it is above green.

To fill a barrel with a volume of 60 liters, using a 5 liter bucket, you need to run 12 times with this bucket to the well. As a result, Peter will spend 3 minutes * 12 times = 36 minutes. Kolya, with his 8 liter bucket, needs 60/8 = 7.5 times. We get a non-integer number. For 7 campaigns, Kolya will bring only 7 * 8 = 56 liters, which is less than necessary. And if Kolya goes for water again, he will bring 64 liters already, which is even more than necessary. As a result, Kolya will need 8 times * 5 minutes = 40 minutes, that is, Petya used to fill his barrel.
The situation changes if it was necessary to bring 56 liters. For this, Kolya needs to run 56/8 = 7 times, and it takes 35 minutes. Petya will need 56/5 = 11.2 times, but since it is an integer that is important, in fact, Petya will need to go 12 times and it will take 12 * 3 = 36 minutes. In this case, Peter will fill his barrel later Kohl.
It turns out that such a strange situation is that the answer to the question of who will fill the barrel faster depends not only on the boys, but also on the size of the barrel. And if you look at the graph, then the places where the graphs intersect quite a lot. Moreover, you can even make Petit's barrel 55.9 liters, that is, less than Kolya’s, and he will fill it anyway later. This fact becomes even more surprising if we calculate the average filling rate of the barrel for Petya and Kolya. In Petit, the average speed is 5/3 = 1.666 liters / minute, and in Kolya 8/5 = 1.600 liters / minute. Kohl may even start half a minute later, and still Petya will be second.
That is, Petya has a faster filling rate and a smaller barrel, and he began earlier, but he will fill his barrel anyway later than Kolya will fill his own.
Such a paradoxical result is obtained precisely because the process of filling the barrel is discrete.
If we consider the case when two opponents in the game hit each other with different strengths and different speeds, then this situation will be similar to barrels and buckets, which we have already considered. And as was shown above, it is not always worth relying on the so-called DPS, that is, on the average damage rate, in assessing the strength of you and your opponent.
Is DPS not applicable at all? Not really. In some cases, it adequately describes the situation.
For each ladder, you can build two parallel lines that will pass through the upper corner points and through the lower ones.

That staircase, which has a higher DPS, after some point will always be higher than the second. And this moment can be found as the intersection of the lower straight ladder of the larger DPS, from the upper straight ladder of the smaller DPS. Here are the formulas for these two straight lines.
fDPSL1 (t) = (DPH1 / Period1) * (t-Period1);
fDPSH2 (t) = (DPH2 / Period2) * t;
DPH1 and DPH2 is the impact force (bucket volume) for the period Period1 and Period2, respectively. DPH1 / Period1 = DPS1. And the intersection of these lines occurs at the moment
T = Period1 / (1-DPS2 / DPS1)
From this formula it is clear that the influence of the discreteness of the situation, and the possibility of the emergence of paradoxes associated with the discreteness, depends on two factors. The first factor is the approximate equality of the DPS of both opponents. In this case, the denominator vanishes, and the time of the termination of the influence of the discreteness of the situation tends to infinity. The second factor is the period of strikes of the person who has a higher DPS. The higher the frequency of strikes, the shorter the period, and hence the time for the termination of the influence of discreteness will be less.
More from the formula for the top straight
fDPSH2 (t) = (DPH2 / Period2) * t
it can be seen that this is just a formula for damage to time with a fixed DPS.
fDPSH2 (t) = DPS2 * t

If the opponents of the DPS are the same, then the one with LESS and the strength and period of the blows will be in the best position. In the limiting case, if the period of strikes tends to zero, then the ladder will turn into a “continuous” straight line of the form fDPSH (t) = DPS * t. And this line is the most profitable option with a fixed PDS.
Thus, if there is a choice to increase the strike force by N% or increase the strike frequency by the same N%, then it is more profitable to increase the frequency, although in both these cases the DPS will increase equally. However, as practice shows, many, due to some intuitive delusions, prefer to increase the impact force.
')
The trap of greed
The problem of merchants is solved in a similar way. Semen spends 5 gold for one trip, gets 10, for a total profit of 5 gold for 3 days. Dobrynya for 2 days gets 3 gold. In 360 days, Simon will make 120 trips and earn 600gold. Dobrynya will earn 360/2 * 3 = 540 gold. As a result, Simon does the right thing, that he carries on, he will earn more than Dobryni. If Simon and Dobrynya agree, and find a way to force the peasants to sell them 3 gold each. Then, in one trip, Simon will receive 7 gold, and Dobrynya 5. For 360 days, Simon will receive 360/3 * 7 = 840, and Dobrynya 360/2 * 5 = 900. That is, Dobrynya will earn more Seeds in 360 days, despite the fact that it will sell its goods cheaper.
In economics, there is such a thing as profitability - the ratio of sales profits to the cost of goods sold.
So, if we consider the ratio of profit to cost, then Seeds profitability may seem higher. In one trip, spending 5 gold, he gets 5gold profits. Dobrynya, for 5 gold, receives only 3 gold profits. But with this approach, as you can see, time is not taken into account at all, and it is necessary to insert it in the cost price as the salary of Semen and Dobryni for transportation. That is, in addition to the money that they invest, you need to take into account the time that they spend. And when it comes to making a profit, about the method of earning, then it is necessary to take into account not only the profit obtained as a result of some actions, but also the time spent on them.
In order to make it clearer, how does it happen that selling at a lower price can be profitable, once again draw a chart. The graph shows the dependence of the profits per unit of time from the cost of goods for 3 different cases. In each case, the product and its cost will be considered the same, but the sale price and time for transportation will be different. Graphs are constructed using a simple formula.
F [Cost Price] = (Selling Price - Cost Price) / Transportation Time
Examples of time and sale prices are taken from the game ArcheAge. Time is measured in minutes, and prices are in gold.
In the first case, Sale Price = 8g, Time = 6 minutes, in the second Sale Price = 11g, Time = 10 minutes, and in the third case Sale Price = 13g, Time = 16 minutes
In the network you can find a table of prices for the sale of all possible goods in the game ArcheAge, for example, here
But, nevertheless, in these tables the distances to points of sale are not indicated, which of course is a big disadvantage.
The real costs of raw materials, which are necessary for the manufacture of goods, in the game vary greatly, due to fluctuations in the gaming market. Prices, generally speaking, are set by players, including the so-called "work points", which are necessary for the production of goods, and which can also be bought on the "market". The cost in this example is approximately 7g, but it can be much more expensive.

Understanding some of the tasks, the process, very often helps to consider extreme cases. If the cost of goods is zero, then all the profit per unit of time is determined by the time that will be spent on transportation. In the general case, all 3 straight lines may not intersect, but in this particular case, at low cost, it is more profitable to carry to the nearest point of sale. If the cost is high, then it may be higher than the selling price at the nearest points, which means that you will work with negative profitability, that is, spend more than you get. And then the only opportunity to earn at least some will be selling in the most remote place, where the selling price is higher than the cost price. But at too high cost, even selling there is not profitable. There is also an intermediate option, when it is most advantageous to carry the average distance.
It is worth noting that the effects associated with the "discreteness" of making a profit are also naturally present here. The principle of analysis of these effects is similar to that discussed above.
When you try to tell such players, you often get in response “Lol ?! I know what to do! What are you teaching me ?! ”. People persist in selling their goods as expensive as possible, and absolutely do not pay attention to how much time they spend on it. Time, however, can be expressed in currency and use this “price of time” in the cost price, and then everything becomes much clearer. But very often there are those who, for the sake of 1 gold, are ready to drive even further, wasting time with much less efficiency. In the end, having been greedy, they lose more.
And what is most interesting, even those who know about these subtleties, very often succumb to the inner momentary temptation, blind erroneous intuition, and the insidious and dangerous feeling of greed, and still the rod to where it is not profitable to sell, but where they see that the sale price of their goods is higher. Psychophysiology - even matan sometimes does not work against it. But this particular feature of human perception is loved to be used by all who feel like it, parasitizing on greedy people.
Wolfram mathematica
Wolfram Mathematica is an extremely powerful tool for solving various tasks of any complexity. However, one should not think that since Mathematica can do so much, it is extremely difficult to use. In fact, I very often use it simply as a very convenient, but also very advanced calculator. There is no need to write code for algorithms. To draw graphs, or quickly create an interactive window, with input fields, sliders and drawing functions in real time, a few simple commands will suffice, which are described in great detail on the heap of examples in the built-in help.
Here is an example of the code for graphing profit / cost graphs.
Mathematica Code
a = {{6, 8}, {10, 11}, {16, 13}}; f[i_, x_] := (a[[i]][[2]] - x)/a[[i]][[1]]; Plot[{f[1, x], f[2, x], f[3, x]}, {x, 0, 13}, PlotStyle -> {Red, Orange, Green}, PlotRange -> All] And a code sample for such a convenient window for drawing discrete processes. You can change the parameters and immediately compare the results obtained on the graph.

Mathematica Code
TotalD[DPH_, CD_, tDelay_, tDuration_] := Table[{n, DPH*(Quotient[n - tDelay, CD])}, {n, 0, tDuration, tDuration/1000}]; (* \ *)(*Quotient \ *) DiffD[DPH1_, CD1_, tDelay1_, DPH2_, CD2_, tDelay2_, tDuration_] := Table[{n, DPH2*(Quotient[n - tDelay2, CD2]) - DPH1*(Quotient[n - tDelay1, CD1])}, {n, 0, tDuration, tDuration/ 1000}];(* \ *) fDPSH[t_, DPH_, CD_, tDelay_] := (DPH/CD)*(t - tDelay);(*fDPSH fDPSH "" \ . *) fDPSL[t_, DPH_, CD_, tDelay_] := (DPH/CD)*(t - CD - tDelay); Manipulate[ Column[{ Row[{ Row[{"DPS1=", Dynamic[N[DPH1/CD1]]}, Frame -> True, FrameStyle -> {Red, Red}], Row[{Dynamic[ If[DPH1/CD1 == DPH2/CD2, " EQUAL ", If[DPH1/CD1 > DPH2/CD2, " MORE THAN ", "LESS THAN "]]]}], Row[{"DPS2=", Dynamic[N[DPH2/CD2]]}, Frame -> True, FrameStyle -> {Green, Green}] }], Show[{ Plot[ {fDPSL[t, DPH1, CD1, Delay1], fDPSH[t, DPH1, CD1, Delay1], fDPSL[t, DPH2, CD2, Delay2], fDPSH[t, DPH2, CD2, Delay2]}, {t, 0, Duration}, PlotStyle -> {Darker[Orange], Darker[Orange], Darker[Blue], Darker[Blue], PlotRange -> All} ], ListLinePlot[ {TotalD[DPH1, CD1, Delay1, Duration], TotalD[DPH2, CD2, Delay2, Duration], DiffD[DPH1, CD1, Delay1, DPH2, CD2, Delay2, Duration]}, PlotStyle -> {Red, Green, Gray}, PlotRange -> All] }, PlotRange -> All] }], {{DPH1, 10, "Value1"}, 0, 100, Appearance -> "Open"}, {{CD1, 0.8, "Period1"}, 0, 20, Appearance -> "Open"}, {{Delay1, 0}, -2, 2, Appearance -> "Open"}, {{DPH2, 8, "Value2"}, 0, 100, Appearance -> "Open"}, {{CD2, 0.7, "Period1"}, 0, 20, Appearance -> "Open"}, {{Delay2, 0}, -2, 2, Appearance -> "Open"}, {{Duration, 10}, 2, 1000, Appearance -> "Open"}, ControlPlacement -> {Right, Right, Right, Right, Right, Right, Right, Right} ] You just need to copy the code into the empty Wolfram Mathematica window and press Shift + Enter. The result you get in the same window.
findings
The Internet is not omniscient. Guides, recipes, manuals for all occasions in it is not found. In each particular case, the refinement, the modernization of well-known methods will allow to achieve the best results. But this requires analyzing the situation, and synthesizing new methods based on known data. But such skills will not arise by themselves, they need to be trained, trained. And sometimes it can be done dull and lazy. There are two ways out: either to try the learning process at school or at a higher education institution, which often seems meaningless and boring, to make it conscious, meaningful and interesting, or, doing something interesting and fascinating, find interesting moments in it, analyze them and try to solve game tasks as complete maths tasks.
If you teach a teacher that is boring and inactive, then this is no reason not to deal with MatAnalysis. In the end, making excuses for a bad teacher, you are more interesting in your life, and you will not make yourself more successful.
Source: https://habr.com/ru/post/283208/
All Articles