Once again on minimizing boolean functions

In the previous article, I described how symmetric cards can rather easily and quickly minimize boolean functions, but did not highlight two points: obtaining different variants of the minimal solution and automating the minimization algorithm itself. I will tell here about it in more detail.



Let me remind you that the minimization task is to find the largest coverage for each unit. If such a coverage is found and it is unique, then it is written into the so-called core of the function, and all units covered by it are excluded from further consideration. However, if the maximum coverage is not the only one, there are solutions that can be used, for example, to take into account any additional requirements. In addition, as I will show later, discarding options leads to the fact that the resulting solution may not be minimal.
')
So, in the example from the previous article, you can find the core of the function for the following symmetrical map:



It is equal to:

! X1 * X5 V X2 * X3 * X4 V X1 *! X2 *! X5

You can find that the unit in the row with the index 0 and the column with the index 4 can be covered in two ways:

! X1 * X3 *! X4 (1)
X3 *! X4 *! X5 (2)

Similarly, a unit in a row with index 10 and a column with index 4 can be covered in four ways:

! X1 * X3 *! X4 (1)
X3 *! X4 *! X5 (2)
! X1 * X2 * X3 (3)
X2 * X3 *! X5 (4)

Note that when covering different units there are identical implicants, denoted here with the same numbers.

Further, the unit in the row with index 30 and the column with index 4 can be covered in three ways:

X3 *! X4 *! X5 (2)
X1 * X3 *! X5 (5)
X2 * X3 *! X5 (4)

And the unit in the row with index 20 and the column with index 1 can be covered in two ways:

X1 *! X2 *! X3 *! X4 (6)
! X2 *! X3 *! X4 * X5 (7)

Since all units should be covered in the final solution, we write the following expression as a product of variants for each unit:

(1 V 2) (1 V 2 V 3 V 4) (2 V 5 V 4) (6 V 7)

Open the first two brackets:

(1 * 1 V 1 * 2 V 1 * 3 V 1 * 4 V 2 * 1 V 2 * 2 V 2 * 3 V 2 * 4) (2 V 5 V 4) (6 V 7)

Since the implicant, being multiplied by itself, gives the same implicant, the first bracket can be rewritten as follows:

(1 V 1 * 2 V 1 * 3 V 1 * 4 V 2 * 1 V 2 V 2 * 3 V 2 * 4) (2 V 5 V 4) (6 V 7)

Further, since the variant with one implicant gives a better solution than with two, you can rewrite the solution in the form:

(1 V 2) (2 V 5 V 4) (6 V 7)

By expanding the brackets further and using similar abbreviations, we get the final solution, which cannot be reduced:

2 (6 V 7)

The first factor 2 is the only implicant in the group and must be added to the core of the function (the so-called extended core of the function):

X3 *! X4 *! X5

A bracket gives two options:

X1 *! X2 *! X3 *! X4

and

! X2 *! X3 *! X4 * X5

You can choose any of them.

Naturally, the question arises about the automation of this algorithm. For this, I wrote the apssymmap program, which can be found on my website:

http://andyplekhanov.narod.ru/soft/soft.htm

It is of interest to compare the results of applying this method with other known methods. Let's compare the results of the work of the apssymmap program with the well-known espresso program using the example below:



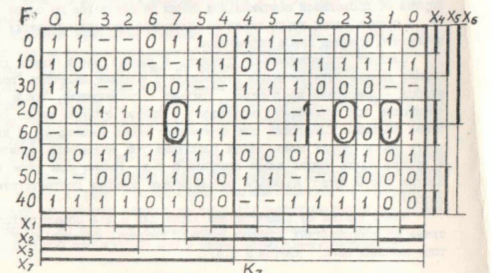
The result of the espresso program:

espresso -Dexact -eoeqntott test.txt



The result of the program apssymmap:



You can see that the apssymmap program provides 8 different options instead of one for espresso. However, a more interesting fact is that the espresso result is not optimal. If we discard all the common parts in these solutions, we can see that espresso will have two implicants left:

! X7 *! X5 *! X4 * X2 * X1
and
X7 *! X6 * X5 * X4 * X3 * X1

containing 5 and 6 variables respectively, and in the apssymmap solution there will be implicants

! X5 * X3 * X2 * X1
and
X7 *! X6 * X3 * X2 * X1

containing 4 and 5 variables, that is, two less. As a conclusion, we can conclude that symmetric cards are not only a more convenient method for manually minimizing Boolean functions, but also superior to other methods for solving this problem on a computer.