Notes with MBC Symposium: more about saddle points

Finally, on the second part of the Surya Ganguli report - as a theoretical understanding of the optimization process can help in practice, namely, what role do the saddle points play (the first part is right here , and it is completely optional to read further).

Disclaimer: The post is written on the basis of the edited chat logs closedcircles.com , hence the style of presentation, and clarifying questions.

I’ll remind you a bit about saddle points. In the space of nonlinear functions, there are points with a zero gradient in all coordinates — namely, the gradient descent tends to them.
If a point has a gradient in all coordinates of 0, then it can be: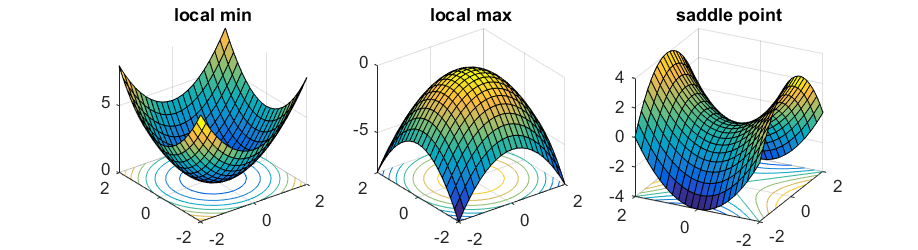

• The local minimum if in all directions the second derivative is positive.
• Local maximum if in all directions the second derivative is negative.
• Saddle point, if in some areas the second derivative is positive, and in others is negative.

So, we are told good news for gradient descent in a very multidimensional space (which is the optimization of the weights of the deep neural network).

• First, the vast majority of points with a zero gradient are saddle points, not minima.
  This can be easily understood intuitively - for a point with a zero gradient to be a local minimum or maximum, the second derivative must have the same sign in all directions , but the more measurements, the greater the chance that at least in some direction the sign will be different.
  And therefore, the most difficult points that will occur will be saddles.
• Secondly, with an increase in the number of parameters, it turns out that all local minima are fairly close to each other and to the global minimum.

Both of these statements were known and theoretically proven for random landscapes in large dimensions.
In collaboration with laboratories Yoshua Bengio, they were experimentally demonstrated for neural networks (theoretically, they have not yet mastered them).

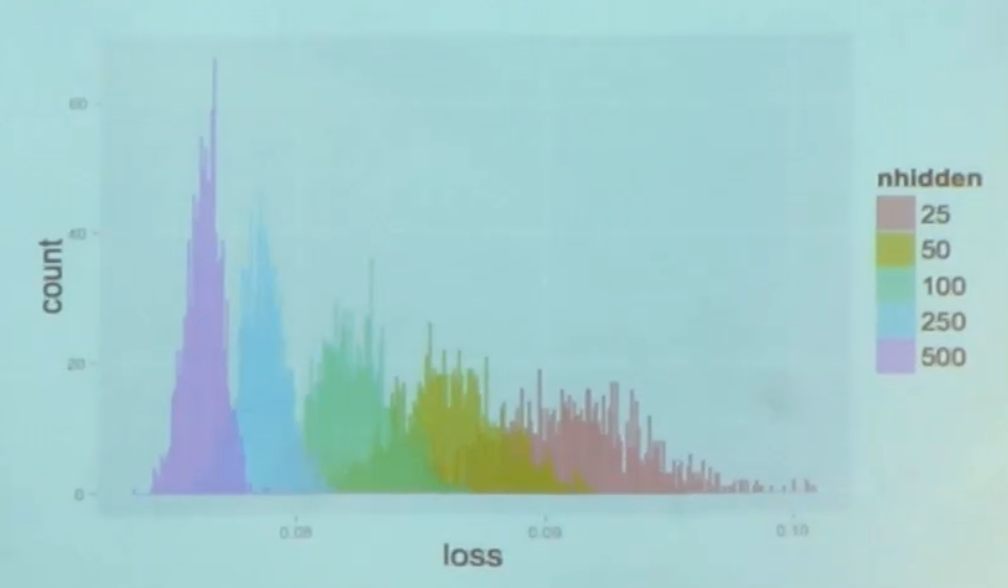
This is a histogram of cost function values ​​in local minima, which were obtained by multiple attempts at training from different points - the smaller the parameters, the smaller the spread of values ​​in the local minima. When there are many parameters, the spread decreases sharply and becomes very close to the global minimum.

The main conclusion is that there is no need to be afraid of local minima, the main problems are with saddle points. Earlier, when we were not able to train neural networks, we thought that this was due to the fact that the system was slipping into a local minimum. It turns out, no, we just could not get out of the saddle point.

And so they came up with a tweak of gradient descent, which well avoids saddle points. Unfortunately, they use Hessian there.

For uneducated people like me, Hessian is a matrix of values ​​of pairwise second derivatives at a point. If you think of the gradient as the first derivative of a function of many variables, the Hessian is the second.
Alexander Vlasov wrote a good tutorial about the so-called second order optimizations, which include working with the Hessian.

Of course, considering Hessian is terribly impractical for modern neural networks, so I don’t know how to use their solution in practice.

The second point is that they invented some theoretically kosher initialization, which in the case of simply linear systems solves the problem of vanishing gradients and allows you to train an arbitrarily deep linear system in the same number of gradient steps.
And they say that it also helps for non-linear systems. True, I have not yet seen references in the literature of the successful use of this technique.
Links to full articles: about optimization of gradient descent and about improved initialization .

In an interesting time we live.