We present data and code in order: optimization and memory, part 1
This two-part series describes how data and memory structures affect performance. Some actions are suggested to improve software performance. Even the simplest actions shown in these articles will lead to significant performance gains. Many articles on program performance optimization consider load parallelization in the following areas: distributed memory (for example, MPI), shared memory or a set of SIMD commands (vectorization), but in fact parallelization must be applied in all three areas. These elements are very important, but memory is also important, and often forgotten about it. Changes to program architecture and the use of parallel processing affect memory and performance.

These articles are intended for mid-level developers. It is assumed that the reader seeks to optimize the performance of programs using common programming capabilities in C ++ and Fortran *. We use assembler and built-in functions for more experienced users. The author recommends those who wish to obtain more detailed materials in order to familiarize themselves with the architecture of processor instruction sets and with numerous research journals that publish excellent articles on the analysis and design of data structures.
There are two basic principles used to bring data and code into order: you need to minimize data movement and place data as close as possible to the area in which they will be used. When data gets into a processor register (or as close as possible to a register), you should use it most efficiently before removing it from memory or away from executable processor units.
')
Consider the three levels at which data can be located. The closest place to executable blocks is the processor registers. The data in the registers can be processed: apply multiplication and addition to them, use them in comparisons and logical operations. In a multi-core processor, each core usually has its own first-level cache (L1). You can very quickly move data from the first-level cache to the register. There may be several cache levels, but usually the last level cache (LLC) is common to all processor cores. The device intermediate cache levels vary for different processor models; These levels can be both common to all nuclei, and separate for each nucleus. On Intel platforms, consistent cache operation is supported within the same platform (even if there are multiple processors). Moving data from the cache to the register is faster than getting data from the main memory.
The schematic data arrangement, proximity to the processor registers and the relative access time are shown in Fig. 1. The closer the block is to the register, the faster the movement and the shorter the delay when the data enters the register for execution. Cache - the fastest memory with the lowest latency. Next in speed - the main memory. There may be several levels of memory, although we will discuss the multi-level memory device in the second part of this article. If the memory pages are located in the virtual memory of the paging file on a hard disk or solid state drive, the speed is significantly reduced. Traditional MPI architecture with sending and receiving data over the network (Ethernet, Infiniband, etc.) has greater latency than receiving data in the local system. The speed when moving data from a remote system with MPI access may vary depending on the connection method used: Ethernet, Infiniband, Intel True Scale or Intel Omni Scale.
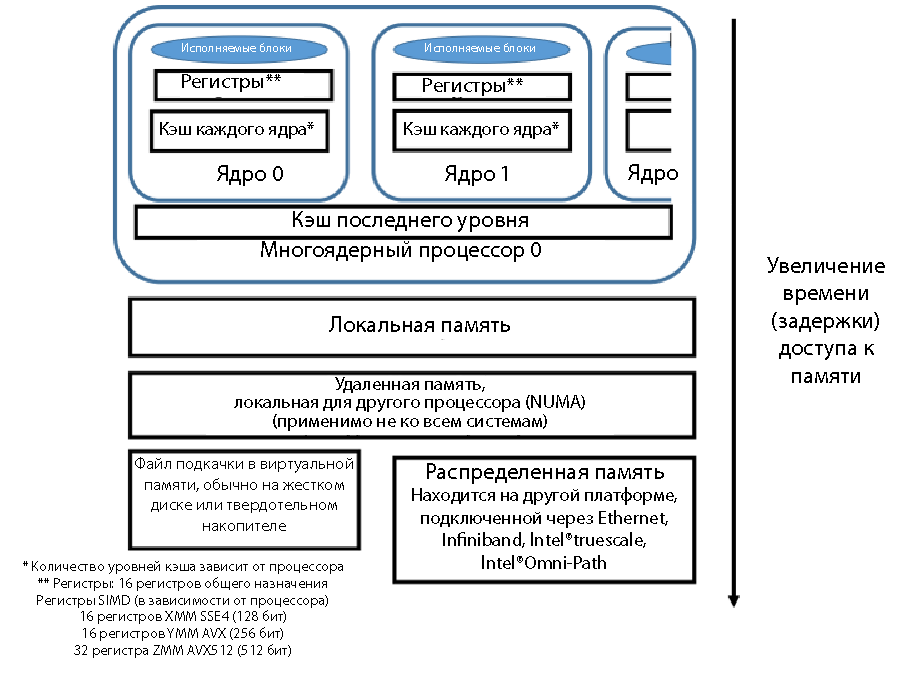
Figure 1. Memory access speed, relative delays in accessing data
The closest place to executable blocks is the processor registers. Due to the number of registers and delays associated with loading data into registers, and also because of the size of the queue of memory operations, it is not possible to use each value in the registers once and submit data quickly enough so that all executable blocks are fully occupied. If the data is close to the executable block, it is advisable to reuse this data before it is pushed out of the cache or removed from the register. Some variables exist only in the form of variable registers and are never stored in main memory. The compiler perfectly recognizes when it is better to use a variable only in a register, so it is not recommended to use the register keyword in C / C ++. The compilers themselves recognize the optimization possibilities quite well and can ignore the register keyword.
The developer must analyze the code, understand how data is used and how long it should exist. Ask yourself: “Should I create a temporary variable?”, “Should I create a temporary array?”, “Do I need to store so many temporary variables?”. In the process of improving performance, you need to collect a performance metric and focus on getting data closer to modules or code branches, which spend considerable time on code execution. Popular programs for acquiring performance data include Intel VTune Amplifier XE, gprof, and Tau *.
An example of matrix multiplication is perfect for understanding this stage. Multiplication of matrices A = A + B * C for three square matrices n x n can be represented by three simple nested for loops, as shown below.
The main problem with this order is that it contains the operation of matrix reduction (lines 138 and 139). The left side of line 139 is a single value. The compiler will partially unfold the loop in line 138 in order to fill the SIMD registers to the greatest extent and form 4 or 8 products from elements B and C, it is necessary to add these products into one value. Adding 4 or 8 products to one position is a casting operation that does not use the performance of parallel computing and does not use all SIMD registers with the highest efficiency. You can improve the performance of parallel processing by minimizing or completely eliminating cast operations. If there is one value in the left part of the line inside the loop, this indicates a possible cast. The data access path for one iteration of line 137 is shown below in fig. 2 (i, j = 2).

Figure 2. Streamlining; single value in matrix A
Sometimes coercion can be eliminated using reordering operations. Consider the ordering in which two internal cycles are swapped. The number of floating point operations remains the same. But since the cast operation (summation of values in the left part of the line) is excluded, the processor can use all executable SIMD blocks and registers. At the same time productivity considerably increases.
After that there is an adjacent appeal to elements A and C.

Figure 3. Updated order with contiguous access
The initial order ijk is a scalar multiplication method. The scalar multiplication of two vectors is used to calculate the value of each element of the matrix A. The order ikj is the operation saxpy (A * X + Y single precision) or daxpy (A * X + Y double precision). The product of one vector per constant is added to another vector. Both the dot product and the operations A * X + Y are BLAS procedures of level 1 . For the order of ikj, no cast is required. A subset of the row of the matrix C is multiplied by the scalar value of the matrix B and added to the subset of the row of the matrix A (the compiler will determine the size of the subsets depending on the size of SIMD registers used - SSE4, AVX or AVX512). Memory access for one iteration of loop 137new is shown above in fig. 3 (again i, j = 2).
The exception to the reduction in scalar multiplication is a significant increase in performance. At the O2 optimization level, both the Intel compiler and gcc * create vectorized code using SIMD registers and executable blocks. In addition, the Intel compiler automatically reverses the cycles j and k. You can verify this in the optimization compiler report, which can be obtained using the opt-report compiler option ( -qopt report in Linux *). The default optimization report is output to the file filename.optrpt. In this case, the optimization report contains the following text fragments.
The report also shows that the reordered cycle was vectorized.
The gcc compiler (version 4.1.2-55) does not automatically reorder loops. The developer should take care of changing the order.
Additional performance gains are provided by locking loops. This facilitates data reuse. In the representation shown above (Fig. 3), for each iteration of the middle cycle, reference is made to two vectors of length n (and a scalar value), each element of these two vectors being used only once. For large values of n, it is likely that each element of the vector will be pushed out of the cache between each iteration of the average cycle. If you lock loops for the purpose of data reuse, performance improves again.
In the last version of the code, the cycles j and k are reordered, and a lock is also applied. The code works on subsets of matrices or blocks of blockSize size. In this simple example, blockSize is a multiple of n code.
In this model, accessing data from one iteration of loop j may look like this.
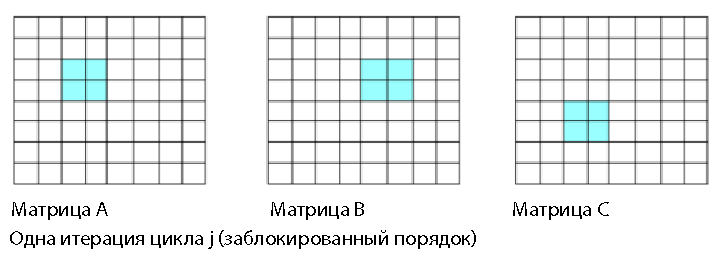
Figure 4. Block model representation
If the block size is correctly selected, it can be assumed that each block will remain in the cache (and even, maybe, in the SIMD registers) during the work of three internal cycles. Each element of the matrices A, B, and C will be used a number of times equal to blockSize before being removed from SIMD registers or displaced from the cache. At the same time, data reuse is increased by the number of times equal to blockSize . When using matrices of small size, the use of blocks practically does not give a gain. The larger the matrix size, the more significant the performance increase.
The table below shows the ratio of performance measured on a system with different compilers. Note that the Intel compiler automatically reverses the loops in lines 137 and 138. Therefore, the Intel compiler's performance is almost the same for orders ijk and ikj. Because of this, the Intel compiler’s baseline performance is also much higher, so the resulting increase in speed over the baseline seems less.
Table 1. Performance Ratio of gcc * and Intel Compilers
The sample code shown is simple, both compilers will create SIMD instructions. This is an outdated gcc compiler, here it is used not to compare the performance of compilers, but to demonstrate the influence of the order of operations and cast, even when the data to be cast is processed in parallel. Many cycles are more complex, the compiler will not be able to recognize the possibilities for parallelization. Therefore, developers are advised to study the parts of the code for which the most time is spent executing, review the compiler's reports in order to understand whether the compiler has applied optimization or whether it should be applied independently. Also note the importance of blocking data if the amount of data becomes too large. For the smaller of the two matrices, performance does not improve. For larger matrices, performance increases significantly. Therefore, before applying blocking, developers should consider the relative size of data and cache. When adding multiple nested loops and corresponding bounds, developers can achieve an increase in performance from 2 to 10 times compared to the original code. This is a significant increase in productivity, achieved with quite a reasonable amount of effort.
As you know, there is no limit to perfection. The block code still does not work at the highest speed: it can be accelerated using the BLAS DGEMM level 3 procedures from the optimized LAPACK libraries, such as the Intel Math Kernel Library (Intel MKL). For conventional linear algebra and Fourier transforms, modern libraries such as the Intel Math Kernel Library provide even more efficient optimization than simple blocking and reordering. Developers are advised to use such optimized libraries whenever possible.
There are such libraries for matrix multiplication, although optimized libraries do not exist for all possible situations in which you can improve performance with blocking. Matrix multiplication is a convenient example to illustrate the principle of optimization. This principle is also suitable for finite difference templates.
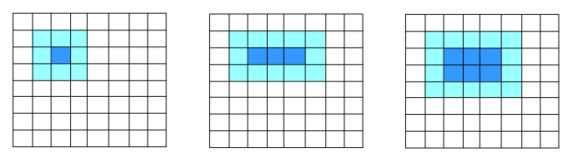
Figure 5. Two-dimensional representation of the block model
A simple nine-point pattern uses the highlighted blocks shown below to update the values in the center block. Nine values are used to update one position. When updating a neighboring element, six of these values will be used again. If the code works in the order shown, then the behavior will be similar to that shown in the adjacent figure, 15 values are used to update the three positions. Further, this ratio is gradually approaching 1: 3.
If you put the data in two-dimensional blocks, as shown in Fig. 5, then for updating six positions 20 values are used, placed in registers in blocks of two; while the ratio is close to 1: 2.
I recommend that readers familiarize themselves with the finite difference technicians in the excellent article Eight methods for optimizing the three-dimensional finite-difference (3DFD) isotropic (ISO) code by Cedric Andreolli (Cedric Andreolli). This article describes not only blocking, but also other methods of memory optimization.
Let's sum up. This article provides three examples that developers can apply to their programs. First, streamline operations to avoid parallel computations. Second, find data reusability and apply a block structure to nested loops to support data reuse. In some cases, this will double the performance. Third, use optimized libraries whenever possible. They are much faster than any code obtained by a regular developer using reordering.
The full code can be downloaded here .
In the second part I will talk about parallelizing the load on several cores, and not just on the SIMD registers. In addition, we will discuss spurious sharing and arrays of structures.

These articles are intended for mid-level developers. It is assumed that the reader seeks to optimize the performance of programs using common programming capabilities in C ++ and Fortran *. We use assembler and built-in functions for more experienced users. The author recommends those who wish to obtain more detailed materials in order to familiarize themselves with the architecture of processor instruction sets and with numerous research journals that publish excellent articles on the analysis and design of data structures.
There are two basic principles used to bring data and code into order: you need to minimize data movement and place data as close as possible to the area in which they will be used. When data gets into a processor register (or as close as possible to a register), you should use it most efficiently before removing it from memory or away from executable processor units.
')
Data placement
Consider the three levels at which data can be located. The closest place to executable blocks is the processor registers. The data in the registers can be processed: apply multiplication and addition to them, use them in comparisons and logical operations. In a multi-core processor, each core usually has its own first-level cache (L1). You can very quickly move data from the first-level cache to the register. There may be several cache levels, but usually the last level cache (LLC) is common to all processor cores. The device intermediate cache levels vary for different processor models; These levels can be both common to all nuclei, and separate for each nucleus. On Intel platforms, consistent cache operation is supported within the same platform (even if there are multiple processors). Moving data from the cache to the register is faster than getting data from the main memory.
The schematic data arrangement, proximity to the processor registers and the relative access time are shown in Fig. 1. The closer the block is to the register, the faster the movement and the shorter the delay when the data enters the register for execution. Cache - the fastest memory with the lowest latency. Next in speed - the main memory. There may be several levels of memory, although we will discuss the multi-level memory device in the second part of this article. If the memory pages are located in the virtual memory of the paging file on a hard disk or solid state drive, the speed is significantly reduced. Traditional MPI architecture with sending and receiving data over the network (Ethernet, Infiniband, etc.) has greater latency than receiving data in the local system. The speed when moving data from a remote system with MPI access may vary depending on the connection method used: Ethernet, Infiniband, Intel True Scale or Intel Omni Scale.

Figure 1. Memory access speed, relative delays in accessing data
The closest place to executable blocks is the processor registers. Due to the number of registers and delays associated with loading data into registers, and also because of the size of the queue of memory operations, it is not possible to use each value in the registers once and submit data quickly enough so that all executable blocks are fully occupied. If the data is close to the executable block, it is advisable to reuse this data before it is pushed out of the cache or removed from the register. Some variables exist only in the form of variable registers and are never stored in main memory. The compiler perfectly recognizes when it is better to use a variable only in a register, so it is not recommended to use the register keyword in C / C ++. The compilers themselves recognize the optimization possibilities quite well and can ignore the register keyword.
The developer must analyze the code, understand how data is used and how long it should exist. Ask yourself: “Should I create a temporary variable?”, “Should I create a temporary array?”, “Do I need to store so many temporary variables?”. In the process of improving performance, you need to collect a performance metric and focus on getting data closer to modules or code branches, which spend considerable time on code execution. Popular programs for acquiring performance data include Intel VTune Amplifier XE, gprof, and Tau *.
Data Usage and Reuse
An example of matrix multiplication is perfect for understanding this stage. Multiplication of matrices A = A + B * C for three square matrices n x n can be represented by three simple nested for loops, as shown below.
for (i=0;i<n; i++) // line 136 for (j = 0; j<n; j++) // line 137 for (k=0;k<n; k++) // line 138 A[i][j] += B[i][k]* C[k][j] ; // line 139 The main problem with this order is that it contains the operation of matrix reduction (lines 138 and 139). The left side of line 139 is a single value. The compiler will partially unfold the loop in line 138 in order to fill the SIMD registers to the greatest extent and form 4 or 8 products from elements B and C, it is necessary to add these products into one value. Adding 4 or 8 products to one position is a casting operation that does not use the performance of parallel computing and does not use all SIMD registers with the highest efficiency. You can improve the performance of parallel processing by minimizing or completely eliminating cast operations. If there is one value in the left part of the line inside the loop, this indicates a possible cast. The data access path for one iteration of line 137 is shown below in fig. 2 (i, j = 2).

Figure 2. Streamlining; single value in matrix A
Sometimes coercion can be eliminated using reordering operations. Consider the ordering in which two internal cycles are swapped. The number of floating point operations remains the same. But since the cast operation (summation of values in the left part of the line) is excluded, the processor can use all executable SIMD blocks and registers. At the same time productivity considerably increases.
for (i=0;i<n; i++) // line 136 for (k = 0; k<n; k++) // line 137new for (j=0;j<n; j++) // line 138new a[i][j] += b[i][k]* c[k][j] ; // line 139 After that there is an adjacent appeal to elements A and C.

Figure 3. Updated order with contiguous access
The initial order ijk is a scalar multiplication method. The scalar multiplication of two vectors is used to calculate the value of each element of the matrix A. The order ikj is the operation saxpy (A * X + Y single precision) or daxpy (A * X + Y double precision). The product of one vector per constant is added to another vector. Both the dot product and the operations A * X + Y are BLAS procedures of level 1 . For the order of ikj, no cast is required. A subset of the row of the matrix C is multiplied by the scalar value of the matrix B and added to the subset of the row of the matrix A (the compiler will determine the size of the subsets depending on the size of SIMD registers used - SSE4, AVX or AVX512). Memory access for one iteration of loop 137new is shown above in fig. 3 (again i, j = 2).
The exception to the reduction in scalar multiplication is a significant increase in performance. At the O2 optimization level, both the Intel compiler and gcc * create vectorized code using SIMD registers and executable blocks. In addition, the Intel compiler automatically reverses the cycles j and k. You can verify this in the optimization compiler report, which can be obtained using the opt-report compiler option ( -qopt report in Linux *). The default optimization report is output to the file filename.optrpt. In this case, the optimization report contains the following text fragments.
LOOP BEGIN at mm.c(136,4) remark #25444: Loopnest Interchanged: ( 1 2 3 ) --> ( 1 3 2 ) The report also shows that the reordered cycle was vectorized.
LOOP BEGIN at mm.c(137,7) remark #15301: PERMUTED LOOP WAS VECTORIZED LOOP END The gcc compiler (version 4.1.2-55) does not automatically reorder loops. The developer should take care of changing the order.
Additional performance gains are provided by locking loops. This facilitates data reuse. In the representation shown above (Fig. 3), for each iteration of the middle cycle, reference is made to two vectors of length n (and a scalar value), each element of these two vectors being used only once. For large values of n, it is likely that each element of the vector will be pushed out of the cache between each iteration of the average cycle. If you lock loops for the purpose of data reuse, performance improves again.
In the last version of the code, the cycles j and k are reordered, and a lock is also applied. The code works on subsets of matrices or blocks of blockSize size. In this simple example, blockSize is a multiple of n code.
for (i = 0; i < n; i+=blockSize) for (k=0; k<n ; k+= blockSize) for (j = 0 ; j < n; j+=blockSize) for (iInner = i; iInner<i+blockSize; iInner++) for (kInner = k ; kInner<k+blockSize; kInner++) for (jInner = j ; jInner<j+blockSize ; jInner++) a[iInner,jInner] += b[iInner,kInner] * c[kInner, jInner] In this model, accessing data from one iteration of loop j may look like this.

Figure 4. Block model representation
If the block size is correctly selected, it can be assumed that each block will remain in the cache (and even, maybe, in the SIMD registers) during the work of three internal cycles. Each element of the matrices A, B, and C will be used a number of times equal to blockSize before being removed from SIMD registers or displaced from the cache. At the same time, data reuse is increased by the number of times equal to blockSize . When using matrices of small size, the use of blocks practically does not give a gain. The larger the matrix size, the more significant the performance increase.
The table below shows the ratio of performance measured on a system with different compilers. Note that the Intel compiler automatically reverses the loops in lines 137 and 138. Therefore, the Intel compiler's performance is almost the same for orders ijk and ikj. Because of this, the Intel compiler’s baseline performance is also much higher, so the resulting increase in speed over the baseline seems less.
| Order | Matrix / block size | Gcc * 4.1.2 -O2, increased speed / performance compared to baseline | Intel 16.1 -O2 compiler, speed / performance improvement over baseline |
|---|---|---|---|
| ijk | 1600 | 1 (basic level) | 12.32 |
| ikj | 1600 | 6.25 | 12.33 |
| Ikj block | 1600/8 | 6.44 | 8.44 |
| ijk | 4,000 | 1 (basic level) | 6.39 |
| ikj | 4,000 | 6.04 | 6.38 |
| Ikj block | 4000/8 | 8.42 | 10.53 |
The sample code shown is simple, both compilers will create SIMD instructions. This is an outdated gcc compiler, here it is used not to compare the performance of compilers, but to demonstrate the influence of the order of operations and cast, even when the data to be cast is processed in parallel. Many cycles are more complex, the compiler will not be able to recognize the possibilities for parallelization. Therefore, developers are advised to study the parts of the code for which the most time is spent executing, review the compiler's reports in order to understand whether the compiler has applied optimization or whether it should be applied independently. Also note the importance of blocking data if the amount of data becomes too large. For the smaller of the two matrices, performance does not improve. For larger matrices, performance increases significantly. Therefore, before applying blocking, developers should consider the relative size of data and cache. When adding multiple nested loops and corresponding bounds, developers can achieve an increase in performance from 2 to 10 times compared to the original code. This is a significant increase in productivity, achieved with quite a reasonable amount of effort.
Using optimized libraries
As you know, there is no limit to perfection. The block code still does not work at the highest speed: it can be accelerated using the BLAS DGEMM level 3 procedures from the optimized LAPACK libraries, such as the Intel Math Kernel Library (Intel MKL). For conventional linear algebra and Fourier transforms, modern libraries such as the Intel Math Kernel Library provide even more efficient optimization than simple blocking and reordering. Developers are advised to use such optimized libraries whenever possible.
There are such libraries for matrix multiplication, although optimized libraries do not exist for all possible situations in which you can improve performance with blocking. Matrix multiplication is a convenient example to illustrate the principle of optimization. This principle is also suitable for finite difference templates.

Figure 5. Two-dimensional representation of the block model
A simple nine-point pattern uses the highlighted blocks shown below to update the values in the center block. Nine values are used to update one position. When updating a neighboring element, six of these values will be used again. If the code works in the order shown, then the behavior will be similar to that shown in the adjacent figure, 15 values are used to update the three positions. Further, this ratio is gradually approaching 1: 3.
If you put the data in two-dimensional blocks, as shown in Fig. 5, then for updating six positions 20 values are used, placed in registers in blocks of two; while the ratio is close to 1: 2.
I recommend that readers familiarize themselves with the finite difference technicians in the excellent article Eight methods for optimizing the three-dimensional finite-difference (3DFD) isotropic (ISO) code by Cedric Andreolli (Cedric Andreolli). This article describes not only blocking, but also other methods of memory optimization.
Conclusion
Let's sum up. This article provides three examples that developers can apply to their programs. First, streamline operations to avoid parallel computations. Second, find data reusability and apply a block structure to nested loops to support data reuse. In some cases, this will double the performance. Third, use optimized libraries whenever possible. They are much faster than any code obtained by a regular developer using reordering.
The full code can be downloaded here .
In the second part I will talk about parallelizing the load on several cores, and not just on the SIMD registers. In addition, we will discuss spurious sharing and arrays of structures.
Source: https://habr.com/ru/post/282738/
All Articles