Monte Carlo method for tree search

The Monte Carlo method is a decision-making algorithm often used in games as the basis of artificial intelligence. He had a strong influence on the programs for the game of Go, although it finds its application in other games, both desktop and conventional computer games (for example, Total War: Rome II ). It is also worth noting that the Monte Carlo method is used in the acclaimed AlphaGo program, which won the 9th Dan go-professional in a series of 5 games.

In this article I would like to tell you about the version of the Monte Carlo algorithm called Upper Confidence bound applied to Trees (UCT). It was after the publication of this algorithm in 2006 that the programs for the game of go greatly strengthened their positions and achieved significant success in the game against a person.

The basis of the UCT algorithm is the solution of the problem of multi-armed bandits. In particular, the Upper Confidence Bound (UCB) algorithm is used. He has already been described on Habré here , but I still repeat the main points.
')
The task is: there is a set of slot machines, each with its own probability of winning. It is required to determine the automaton that will bring more winnings.

UCB Algorithm:
1. Initialization. Play on each machine once
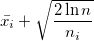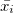2. At each subsequent iteration, select the machine with the maximum value where This is the average winnings of the i-th machine, 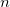number of games on all machines, and the number of games played on the i-th machine.

In practice, a modification of the UCB formula is often used to search the board game's move tree.

For example, this: ,

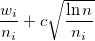here this is the number of wins of the i-th node. - the number of visits to the i-th node, and 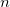the number of visits to all adjacent nodes. c is a constant used to set the desired balance between the width and depth of the search. The larger it is, the deeper the search will be.

As the name implies, the UCT algorithm (Upper Confidence bound applied to Trees) uses the UCB approach to search the tree. Consider step by step each phase of the algorithm:


The first phase, the choice . We consider each position as a task of a multi-armed gangster. Nodes at each stage are selected according to the UCB algorithm. This phase is valid until a node is found in which not all subsidiaries have victory statistics. In the figure, the first value in a node is the number of wins, the second total number of games in this node.


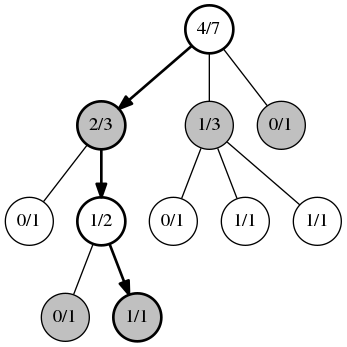
Second phase expansion . When the UCB algorithm can no longer be applicable, a new child node is added.


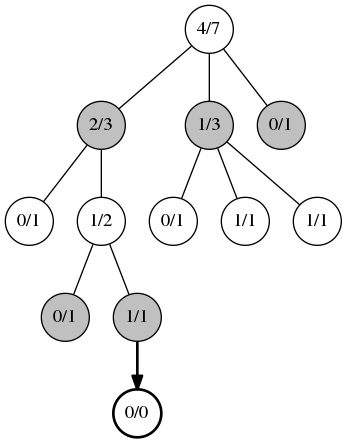
The third phase, simulation . From the node created at the previous stage, the game starts with random or, in the case of heuristics, not entirely random moves. The game goes to the end of the game. Here only the information about the winner is important, the position evaluation does not matter.


The fourth phase, the reverse spread . At this stage, information about the game played is distributed up the tree, updating the information in each of the previously passed nodes. Each of these nodes increases the number of games, and the nodes that match the winner also increase the number of wins. At the end of the algorithm, the node visited the most times is selected .

UCT does not always choose only the best move, but also periodically examines less successful nodes. The second parameter of the formula is slowly growing for those sites that are visited less frequently. And in the end, at some stage, the algorithm will choose just such a move as the preferred one. If the move meets expectations, it will be more likely to be selected next time.

Compared with other algorithms for finding optimal moves, UCT has the following advantages:

• UCT can be safely stopped at any stage of work. And at the time of stopping, he will calculate evenly all the moves from the root node
  
  An example of stopping the alpha beta algorithm. It can be seen that the nodes with the “?” Sign have not been investigated.
  
• The tree grows asymmetrically, exploring the preferred moves deeper than the others. Thus, greater efficiency is achieved in comparison with other algorithms in games with a significant number of options for enumeration.
  

Since Since the moves chosen randomly are mostly meaningless and do not have a general direction, various heuristic methods based on information about a particular game are used to improve the performance of the algorithm. One of these methods is the use of templates.

Here is an example of a 3x3 pattern for cutting stones in Go:

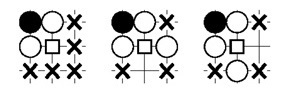
The move will be regarded as interesting when the first pattern matches, but the second and third ones do not. That is, the white group can be "cut." The square shows the position of interest to us.

Templates can be used both at the stage of selecting a move in the tree, and at the stage of simulation. Often, such patterns are searched somewhere in the vicinity of the last move made. This is done because the current move is not rarely a response to the previous one and is likely to be made somewhere nearby.

An example from the series before and after. On the left, the game situation with the use of the usual UCT, on the right UCT with the use of templates:

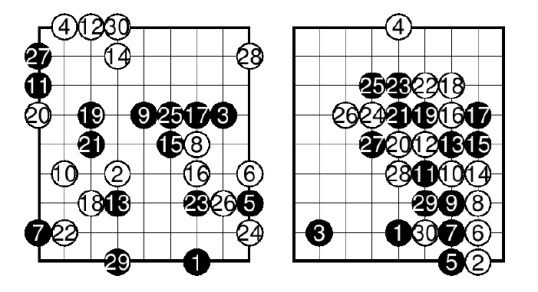
It can be seen that in the first picture the stones are arranged haphazardly across the board.

In most cases, templates are written by hand, but there are also examples of automatic generation.

In order not to be sprayed on the whole board and not to waste time on the miscalculation of unnecessary options. One can single out the most important area in which one can already explore the moves. Obviously, if at the moment the whole struggle is concentrated around one group in a certain corner of the board, then it does not make sense to consider the empty areas around. Algorithms for determining such areas are beyond the scope of the article, but those who are interested can read in detail here: Common Fate Graph .

The UCT algorithm can be simultaneously run in multiple threads. Here are some ways to parallelize calculations:

• Parallelization of nodes, simultaneous simulation of games from the same node.
• Parallelization of the root, building independent trees.
• Parallelization of a tree, joint construction of a single tree by several threads.

This is probably all that I would like to say about the Monte Carlo algorithm and in particular the UCT. In general, the algorithm with additional modifications shows good game results. In favor of this statement says, that all modern Go-programs use it. I hope that for some of you it will also be useful.