Mathematical model of perception (Part 2)
Part 1
Part 3
Recently, marked by the loud triumph of the industrial introduction of artificial neural networks. Find out whether a word or a person, choose a melody according to his mood are tasks that can be considered with confidence already solved. The media is full of now and then emerging headlines about creating artificial intelligence, and science fiction writers argue about whether a thought can spontaneously originate in such networks. But is success really so grandiose, after all, to distinguish between numbers does not mean to have an abstraction of numbers, but to skillfully draw up sentences does not mean to be able to determine their meaning.
Let's try to look at these problems from a slightly different angle. In nature there is one process well-founded by it — evolution: everything that cannot adapt usually dies out. It was the task of adaptation at a certain stage that caused the development in living beings of the ability to perceive the properties of the external world, and the need to respond promptly to changes in these properties encouraged the development of animals in the nervous system. Is it therefore worth trying to imagine which tasks and in which complicating sequence the developing animal intellect had to be solved, because then, having solved them, we may repeat the path of evolution and finally get closer to understanding the mechanisms of thinking. The second seemingly reasonable idea is to start designing machines capable of making an idea about something (the fact of the presence of a mirror-symmetric fragment in the picture, or that the labyrinth under study has a way out) try:
1) call it “something” in terms of the perception of the machine;
2) to characterize the class of all those concepts that can be represented by the machine of this design.
However, to call what such basic concepts as “time” and “space” are, not within the framework of any formal theory, but by its nature, may turn out to be an insoluble problem. Here it is saved that in many cases the process of perception can be formally replaced by a (multi) character sequence depicting the states of the receptors at equal, rather short intervals of time. After such a substitution, the true nature of the concepts to be perceived is no longer important - only what they are in terms of the said symbol sequence is important. From this new position it is interesting to consider such concepts as “time”, “place”, “number”, “memory”, “future”. In this part of my work, I tried to find an approach to the definition of the concept of symmetry and the concept of form, as well as to show how they are actually implemented with the example of a “visual probe”. If you have not read the first part of the article , I recommend that you do this, because the parts are not independent and the further content may not be clear.
Mathematics knows many examples when certain properties cannot be established "from the inside." Perhaps the most famous of them is the statement that it is impossible to establish its consistency only by means of arithmetic. The other says that it is impossible to describe it in any language, which of its phrases are truths in order not to miss anything and not to come but to a contradiction. In general, self-determination and self-descriptiveness are frequent causes of various paradoxes and antimonies. I wonder what a probe can “say” about itself? It is meant what qualities and properties of the probe a person can make up only on the basis of the experience of observing his indicators. For example, looking at the probe at least once, as on an object, it is difficult not to notice its symmetry. But can the probe itself "notice" it, because it has no way to "see itself"? Quite unexpectedly, it turns out that it is possible to form an idea of all the symmetries of the probe solely by the patterns of change in the color of cells perceived by its receptors. The method by which this can be done is devoted to the nearest story.
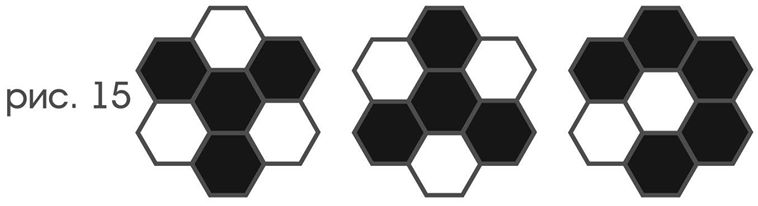
To begin with, we will find for everyone involved in the further description of the probe the concept of its “indicator double”. Methods for coloring seven cells surveyed by a probe are called color configurations. Since the probe can appear in different positions over the same cells (say, if there are turns among its simple movements), then, to be more precise, by the color configuration we mean a comprehensive description of what color each of its color-sensitive receptors is . Different color configurations are shown in Figure 15.
')
The dual concept of a color configuration is an understanding of a color configuration in an improper sense — an exhaustive description of which color indicators of the probe are on and which are not.
Since, by assumption, a simple movement occurs exactly when the color indicator that represents it goes out, these phenomena turn out to be dual to each other, and it is reasonable to call the latter a simple movement in an improper sense. A series of consecutive simple motions is called a general or composite motion. Any simple movement, as a series of length 1, is, with such a definition, including a general one. The phenomenon consisting in the fact that first only the ∆_1 lamp goes out, then only the ∆_2 lamp, ..., then only the ∆_n lamp and then between these moments not a single motion indicator is dual to the general movement, will be dual to the general movement.
This phenomenon Σ, depicted as ∆_1 * ∆_2 * ... * ∆_n, by virtue of the definition of simple motion in an improper sense, turns out to be a general motion in an improper sense.
It is easy to see that if Σ_1, Σ_2, ... Σ_k are common movements (in their own or improper sense), then the general movement will be the phenomenon Σ_1 * Σ_2 * ... * Σ_k, when Σ_1 first occurs, then Σ_2, ..., then Σ_k, and there are no movements between two of these movements following one another.
Some complex movements (in the proper sense) actually, in their completion, leave the probe in the same place in the same position. Therefore, they should be called stationary. Those, for example, are ↑ * ↓, ↖ * ↗ * ↓ and ↷ * ↶. Is it possible to determine the dual property of stationarity with respect to general movements in an improper sense? Direct translation of the formulation of this property would require a preliminary definition in terms of indicators of the concepts “place on the hexagonal lattice” and “probe position”, which we do not yet have. Let's try to find an indirect path. We note first that every time the color configuration observed before performing any stationary movement is exactly the same as after its completion. In this sense, all stationary movements "retain" color configurations. In fact, if the hexagonal grid is colored quite diverse, there are no other movements that preserve color configurations. These two circumstances speak of the equivalence of the properties “stationarity” and “movement to preserve color configurations”, the last of which is easily translated into the language of indicators: it is only necessary to perceive the terms “movement” and “color configuration” in an improper sense. The equivalence mentioned above gives us the right to consider this translation as a property dual to the property of stationarity. To express the stationarity property of the motion Σ (in proper or improper sense), we will use the formal notation Σ ≃E.
The movements of U and V such that their sequential execution in any order is a stationary movement (U * V≃E and V * U≃E), it is reasonable to call them reciprocal. Such are, for example, the pairs ↑ and ↓, and, ↷and ↶, (↖ * ↗) and ↓ among proper motions, as well as n [↑] and n [↓], n [↖] and n [↘], n [↷] and n [↶], (n [↖] * n [↗]) and n [↓] are among the improper ones.
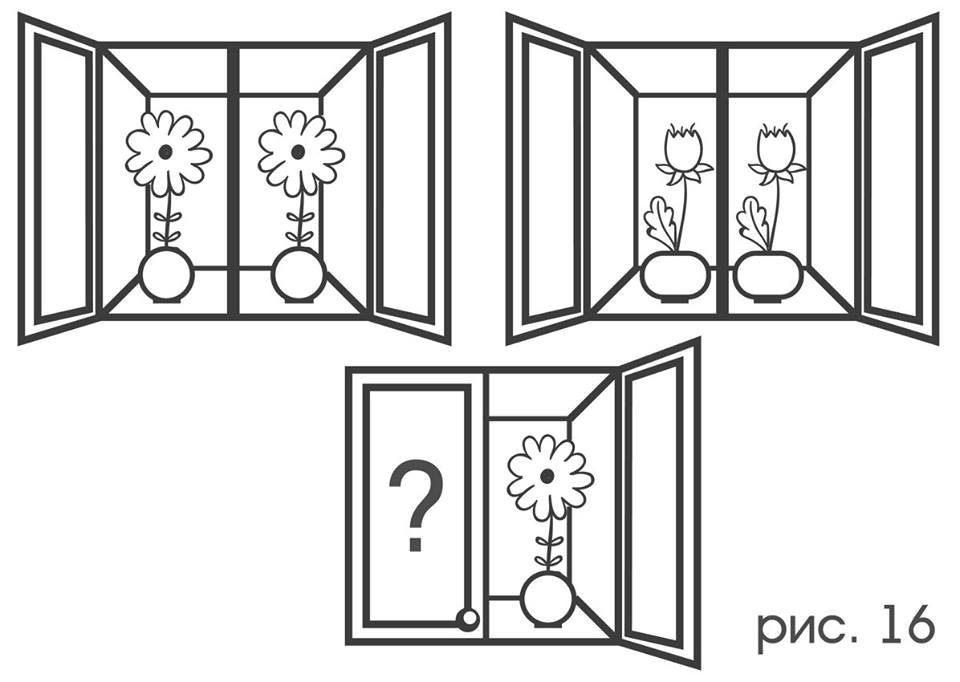
Is it possible to extend the application of the “≃” equivalence sign to non-stationary motions? Thus, the general motion of ↑ and (↖ * ↗), being different in the method of implementation, in fact, leads to the same result. In general, if two instructions for the result of their execution, give the same movement of the probe, this fact can always be established by the form of these instructions. For example, wherever the probe is, executing either: “shift ↑, shift, then”, or: “shift ↖, then ↷, shift ↑” will change its position and position in the same way. “Equivalence” of two types of movements can be noticed also by direct observation of their implementation by the probe on the hexagonal lattice: in both cases it is enough to describe the final position in terms of initial, (for example, “after each U movement is completed, the probe is shifted by seven cells in the direction of "4", one cell in the direction of "6" and rotated 60 ° counterclockwise, counting from its position at the time of the start of this movement "). If the descriptions are the same, then the types are "equivalent." Nevertheless, there seems to be no simple way to establish the “equivalence” of movements in observing only the probe indicators. Here, the situation vaguely resembles the following: suppose there are many two-door wardrobes, behind each door of which there is a camomile or tulip hiding, and the flowers inside the same wardrobe are always the same: either are both daisies or tulips (Figure 16).
But is it possible to guess this pattern, if only one door can be opened in each cabinet? Watching the indicators it is difficult to understand that any two movements (in an improper sense) would always lead to the same changes in color configurations. Indeed, in reality, only one of these movements is performed each time. The impossibility of a simple definition of "equivalence" makes it somewhat difficult to use conventional algebraic methods in constructing a "probe theory" and forces us to use a strongly curtailed analogue of equivalence - stationarity. However, several useful rules of algebraic character can still be expressed:
i) Let U and V be stationary motions, then the motions of U * V and V * U will also be stationary;
ii) Let U * V be stationary motions, then whatever the stationary motion Σ, the motion U * Σ * V is also stationary.
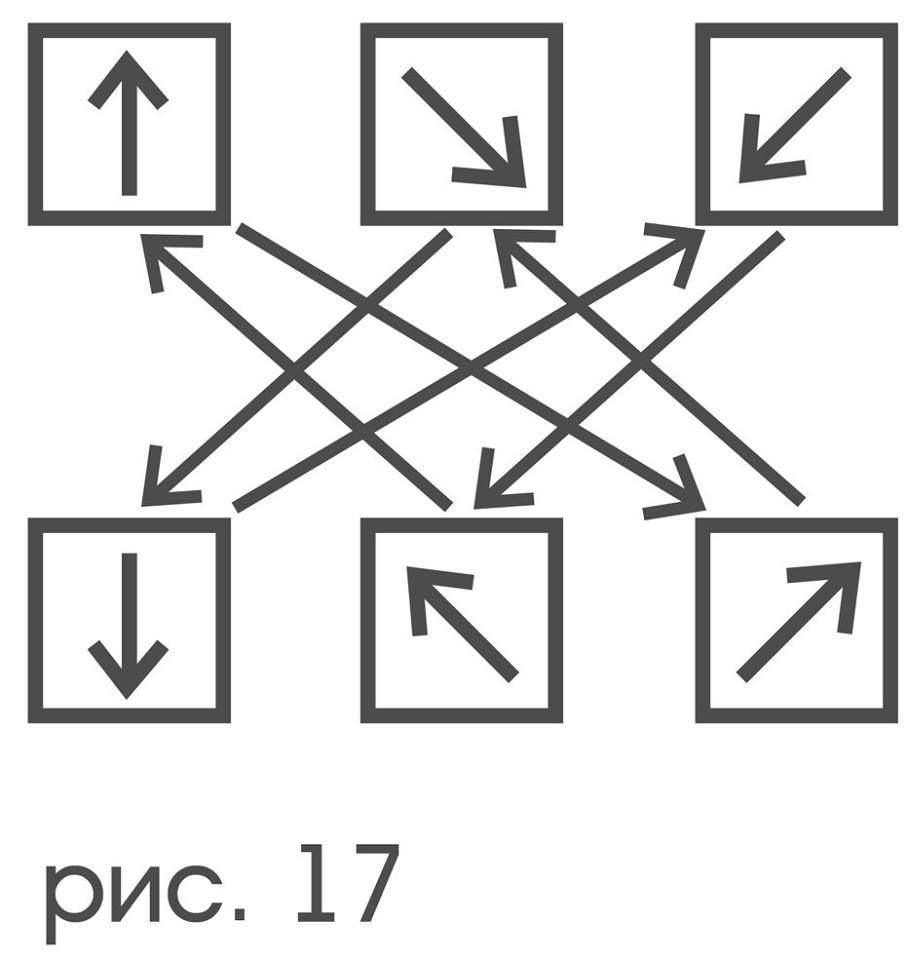
The proof of the above rules, when all the terms are understood in the proper sense, follows from the definition of stationarity - the properties of movements ultimately do not change the position of the probe, and due to the duality principle, these rules are also true in the improper case. In the same way, by proving any statement about the projective plane, you can, by virtue of the duality principle of projective geometry, be considered proven and the statement obtained from the proven by replacing the words “point” with “straight line” and “direct” with “point”. An example of one more important property for describing a probe, generalizing the property of mutual reversibility, is demonstrated by a triple of motions - ↖, ↗, ↓. We agree to say that the motions of U, V, and W form a cyclic triple if their execution in any order leads to stationary motion. A simple analysis shows that among the elementary displacements there are exactly two cyclic triples: (, ↗, ↓) and (↙, ↘, ↑), which are obtained from each other by replacing their constituent motions with the reverse ones. It has already been shown how, observing the indicators, to select among them six light bulbs representing elementary displacements, but no actual way is given to indicate which of these light bulbs represents, say, the displacement, but which. Looking ahead, we warn the reader that there is simply no such way, due to the symmetry of the probe and the arbitrariness of its connection with the dial, but the dual nature of the cyclical properties and reciprocal reversibility makes it possible in the six lamps to indicate pairs corresponding to pairs of reciprocal movements, and triples corresponding to cyclic triples. For simplicity, we will talk about reciprocal indicators and their cyclic triples. It turns out that these two properties are quite enough to express in dual terms the concept of symmetry of the probe as an object. A probe as an object can be “superimposed upon itself”, turning it over like a coin, or turned around a central receptor. Any such “overlay” defines a permutation between the marks “12”, “2”, “4”, ..., “10” of the dial associated with it. For example, when turning by 60 degrees in the clockwise direction, "12" is superimposed on "2", "2" - on "4", ..., "10" - on "12". This permutation in view of the accepted correspondence between dial marks and elementary displacements generates a permutation: "↑" → "↗" → "↘" → "↓" → "↙" → "↖" → "↑". The latter, as can be seen in Figure 17, retains the properties of cyclicity and mutual reversibility in the sense that if the two displacements are reciprocal, then they are translated into reciprocal, and if some three of them form a cyclic triple, then their images also form a cyclic triple .
In fact, the described situation with preservation of cyclicity and mutual reversibility is not accidental: the numbers corresponding to reciprocal movements are diametrically opposed to the dial of the ball, the corresponding cyclic triples are located at the ends of the correct three-pointed "stars" (Fig. 18), and any overlap of the probe on itself certainly retains the diametrical opposite of its points and the shape of the “stars”.

By simple reasoning, it can be shown that the opposite: every permutation among elementary displacements that preserves the property of mutual reversibility and cyclicity is generated exactly by one imposition of the probe on itself.
The set of all such permutations is called the group of internal symmetries of the probe. This name is justified by the following fact. Give some names to all the color indicators (we denote the set of names involved in this case by K) and all the indicators representing elementary displacements (we denote the corresponding set by M). A sufficiently detailed description of the probe (as a system of patterns of indicator states) will be a list L of all such triples of names x, y, p, for which the indicator of color x lies in the direction of the elementary displacement represented by indicator p from the indicator of color y (in an improper sense). Let m be the permutation of the names of the color indicators on M, and k the permutation of the names of the indicators representing the elementary displacements on K. What if we perform these permutations simultaneously within the list L? Generally speaking, both the look of the list and the meaning that it contains can change after that. However, if k and m are generated by some superposition of the probe on themselves, then the only result of the mutual implementation of these permutations in the list will be a change in the order of enumeration of triples, which does not affect its meaning.
Suppose now that some m and k after their execution on the list L change in it, except that only the order of the triples, it turns out that the opposite is true: they must be generated by some imposition of the probe on themselves (as an object), and all such m form an isomorphic group internal symmetry of the probe. In more detail about the connection of symmetries of an object with the symmetries of its descriptions will be discussed in the next chapter.
How to define the concept of form? Let's imagine how his children comprehend. Take, for example, the educational game for the smallest ones - a wooden puzzle is a set of objects of different geometric shapes and a board with holes suitable for the shapes of objects. A child solves a difficult task for himself: what form should an object be, so that it can be inserted into a hole. The first success in this game is waiting for him with a round-shaped element - it is symmetrical about turns and is easily recognizable. But with the element of the puzzle in the form of a box, accidentally turning it over, the child will have to tinker pretty.
Watching birds, especially ravens and parrots, is easy to see, as they look at objects, they tilt their heads to the right, then to the left. It is known that many living creatures (including more simple than the crows) are able to recognize objects in their mirror image, whereas you can see the reflected object in its reference position only by changing the eyes and turning the retina in them.
The concept of the form of things does not apply only to visual perception: people easily recognize favorite tunes, even if you play these tunes a little differently than in the original: an octave higher or lower, in slow motion or in an accelerated one; even if the melody is whistled, you can still recognize it. Is music therefore a form of a sequence of sounds?
It turns out that often the form or symmetry of a thing can be judged only by its description. This method is preferable in that it does not require any manipulations with the thing itself and, perhaps, it allows one to recognize the melodies without being able to slow down or speed up the time or change the octave of the sound, and the shape of the objects without tilting the head or pushing them through the holes.
Things themselves, both real and mathematical abstractions, in most cases are collections of simpler things that are in certain relationships with each other: a brick wall is a collection of bricks arranged in a certain way relative to each other, a work team is a collection of people connected by relations subordination.
As another example, we will consider an arbitrary triangle, as a set of three segments with the relations “have length” and “have a common end”.
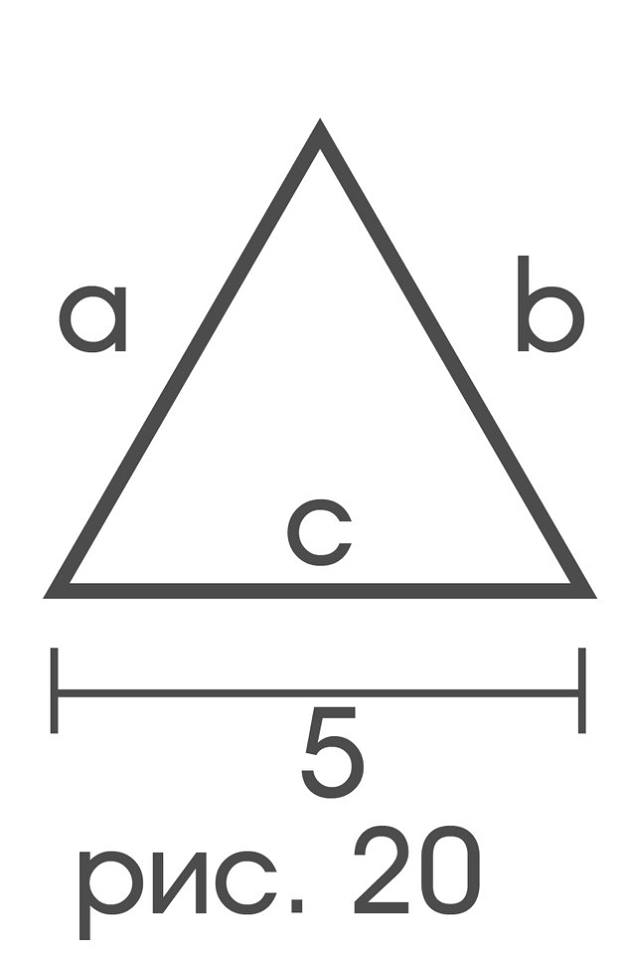
In these terms, the equilateral triangle in Figure 20 admits the following comprehensive description:
“The triangle ∆ is the set of three segments a, b, c, and:
1) one of the ends of a is common with b, the other with c, the length of a is 5;
2) one of the ends of b- is common with c, the other is from a, length b is 5;
3) one of the ends of c is common with a, the other with b, length c is equal to 5
".
It is difficult not to notice the surprising symmetry of this description, which to some extent reflects in itself all the symmetries of the triangle it defines. To give the above, greater clarity, we impose a triangle on ourselves, turning 120 degrees (Fig. 21).
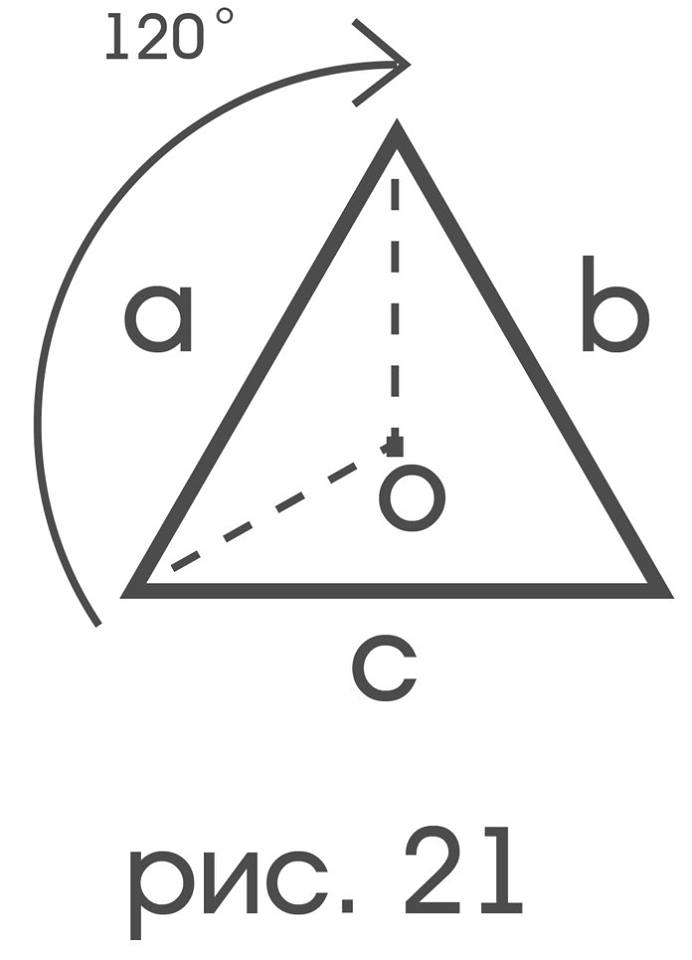
Upon completion of this movement, a will move “to the place” b, b - “to the place” c, c in turn - “to the place” a. If we formally carry out the written permutation in the description of ∆, we get the following:
“The triangle ∆ is the set of three segments a, b, c, and:
1) one of the ends b is common with c, the other with a, length b is 5;
2) one of the ends of c is common with a, the other with b, length c is equal to 5
3) one of the ends of a is common with b, the other with c, length a is equal to 5
".
This shows that as a result of this substitution, the description of ∆, with the exception of an insignificant change in the order of transfer, completely preserves its form. As the reader may guess, the reverse is also true: any permutation among a, b, c, preserving, with the mentioned reservation, the type of description ∆, is generated by some of its geometric symmetry.
Such a duality between the symmetries of a thing and the symmetries of its description does not always occur. Of course, if the description already has some symmetry (there is a permutation of the names of things appearing inside the description that do not change its appearance), then it is necessarily generated by the symmetry of the thing. The reverse, however, is not true: the same one-sided triangle can be given a description that does not have any symmetries except the identical one:
“The triangle ∆ is the set of three segments a, b, c, and:
1) one of the ends of a is common with b, the other with c;
2) one of the ends b is common with c, the other with a;
3) one of the ends of c is common with a, the other with b;
4) length a is equal to 5;
5) the angle between a and b is 60 °;
6) the angle between b and c is 60 °. "

Let us pay attention now to the case when the thing is a graph. Each graph can be considered as a collection of vertices with a two-place relation “... connected by an edge with ...”, and to get an exhaustive description of a particular graph, it is sufficient to simply list all the pairs of its vertices that are in this respect. We describe this description as a list of incidents. For clarity, the vertices of the graph can be imagined as buttons, and the edges connecting them - threads.
Any overlay (mapping a set of vertices of a graph onto itself), in which exactly one vertex is superimposed on each vertex and exactly one edge on each edge, is naturally called the symmetry of this graph, if overlapping with the listed conditions is possible between two different graphs, it is natural to talk about isomorphism between graphs of the same form .
Let the reader be an easy exercise to show that every symmetry of a graph corresponds (dually) to some symmetry of its list of incidents, and two graphs have the same form if and only if the list of incidents of one can be obtained from the list of incidents of the other by simply replacing (exact substitution) vertices in this list.
Figure 23 shows three differently colored instances of the same graph.
Probably the most immediate way to get a description of an instance of a graph with a selected coloring is to add to the list of its incidents an enumeration of what color each of its vertices has. It is obvious that not all symmetries, exactly as not all graph isomorphisms, leave the chosen coloring unchanged: since when you try to impose the specimen No. 1 on yourself by turning 90 °, each vertex will be applied to the vertex of the opposite color. Therefore, it is reasonable that the symmetries of a colored graph, in which only vertices of the same color overlap, are called the symmetries of the chosen coloring, and if an isomorphism with the described property is possible between two graphs, then talk about the isomorphism between the coloring of two graphs of the same form (or about the same with accuracy before this form isomorphism coloring).According to these definitions, the coloring of copies No. 1 and No. 2 have the same shape, which differs from the coloring form of copy No. 3.
But what to do if there is no physical way to overlay some columns on others? How then to determine the shape of the coloring? Let again for the reader it will be a simple exercise to show that any symmetry of the selected coloring of the graph corresponds (dual) to such a permutation of the names of its vertices, which preserves both the list of incidents and the list of colors of the vertices. Colorings of two different graphs have the same form if and only if both mentioned lists for one of them can be obtained from the lists for the other by a simple substitution (exact substitution) of the names of their vertices.
Now it is time to shed some light on how the shape comparison of objects takes place. The most convenient way to do this is using the example of a probe already familiar to us, and the consideration will touch the extreme case of the constraint of its simple movements, when the latter are limited exclusively by elementary displacements. It turns out that it is already enough of them to say with respect to the color configurations of the lattice cells in Fig. 24 that the flags a) and b)
one form up to “rotation”, flags b) and c) one form up to “specular reflection”, while the probe itself, I emphasize once more, is deprived of any opportunity to turn or “mirror reflect”. In the described situation, the concepts of “rotation” and “mirror reflection” will receive correct definitions by purely linguistic methods. In many ways, all of the above is possible due to the remarkable fact that, like the lattice area in the “field of view of the probe,” the probe itself has exactly the same set of symmetries that the “umbrella” graph of Figure 25 has.
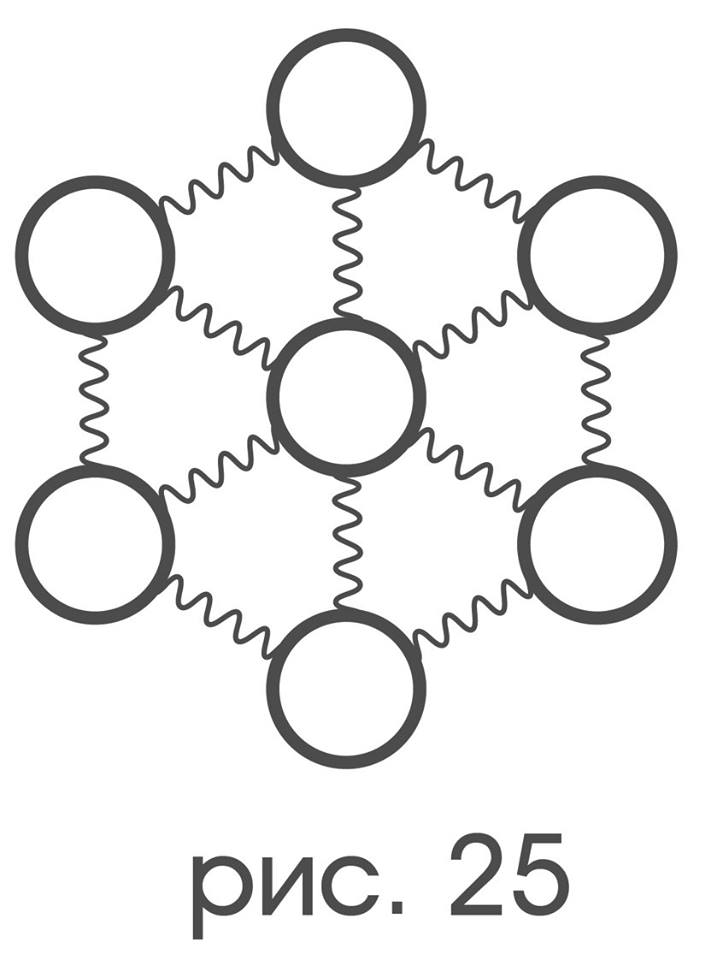
In order to give the promised way of comparing the forms of color spots, it will be shown how to enter a structure that turns each of these sets into an umbrella graph on a set of cells under a probe, a set of color sensory receptors and a set of receptor-related indicator indicators. Thus, the task of comparing the forms of color spots will be equivalent to the problem of comparing the forms of coloring of an umbrella graph.
The idea of solving the latter without involving geometrical concepts that are not yet defined in a vicious circle is to judge the symmetries of the umbrella graph by the symmetries of its description. But this is where the problem arises: which of these symmetries should be called reflections, and which turns (the umbrella graph does not have other symmetries), because without realizing the direct manipulation of the thing, the meaning of the words “reflection” and “rotation” is lost, while Description when performing permutations of names in it does not rotate or reflect?
One of the ways to return the lost meaning is to find the categorical property of the permutations corresponding to each specific type of symmetry. The orbit structure is a suitable and proven property for this purpose. So symmetry, in the intuitive understanding of which is a rotation of 60 °, corresponds to a permutation

and only turns of 60 ° have the structure of orbits π :

Symmetries, in the intuitive understanding of which are mirror reflections, and only they have structure I :

The structure of orbits E :
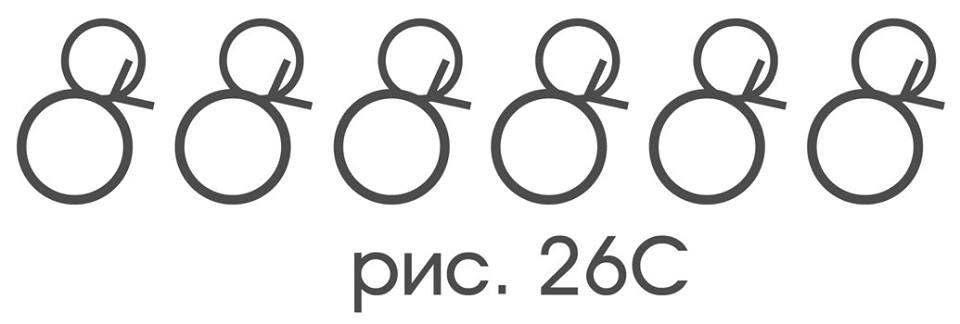
only identical symmetry,
the structure
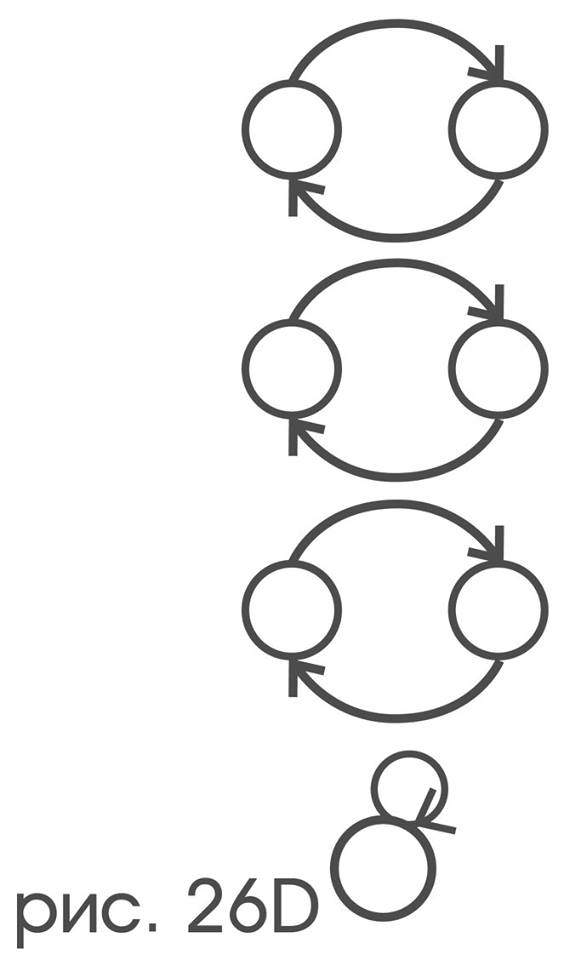
is only a 180 ° rotation,
and only “a 120 ° rotation” unambiguously corresponds to the structure:

This completes the enumeration of all possible types of symmetries of the umbrella graph.
Let's transform the lattice region, which is the “field of view” of the probe, into a graph, the vertices of which are the cells of this region, and the edges between them represent the relation “to be adjacent on the side” (Fig. 27).

Such a metamorphosis makes it possible to compare the images viewed by the probe, as the coloring of the resulting graph, by analyzing their descriptions, without requiring any "physical" possibility to impose something on each other. For example, the color configurations in Fig. 24 correspond to the coloring of a '), b'), c ') of the umbrella graph (Fig. 28), moreover, if under the “rotation”
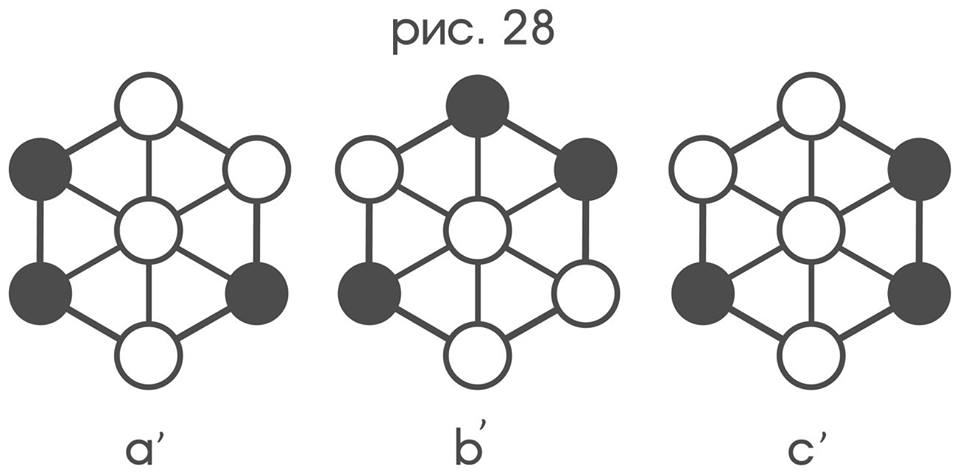
and “mirror reflection” to understand that the orbits have permutations that correspond to isomorphisms of colorings of a particular structure, then a ') and b') really have the same shape with an accuracy of 120 °, and b ') and c') with accuracy before mirroring.
The reader probably drew attention to the fact that from the very beginning the probe was depicted in the form of an umbrella graph with receptors-tops and rigid rods-ribs. One could therefore say that comparing the shape of color configurations on its receptors again comes down to analyzing the descriptions of the colorings of the above graph, however, hard rods cannot be seen with the help of receptors or make a picture of them from observing the indicators. However, there is still a way to turn multiple receptors into a perceptible umbrella graph with the same structure: all you need to do is note that the x receptor is “connected by a rod” with the y receptor exactly when the relationship is:
“There is an elementary displacement of S such that x lies in the direction of S from y”. It is in this place that the presence of all elementary displacements among the simple movements of the probe is important, since then the justice or the injustice of the latter by the relationship between specific x and y receptors can be established by sufficiently long observation of the colors perceived by them. Another observation is that elementary displacements among simple movements are sufficient to judge the uniformity of form and two configurations obtained from each other by turning or mirroring, even when the probe itself cannot in principle be rotated or mirrored.
It remains to note that the phrase “∃ S (S is an elementary displacement) (x lies in the direction S from y)” allows direct translation into dual terms, thereby defining the dual relation on the set of color indicators, which turns this set into an umbrella graph. The latter means that only by observing the bouquets of lamps associated with the probe, even when all its simple movements are reduced to plane-parallel displacements and the probe itself is not directly observable, it is still possible to adequately and exclusively in internal terms define the concepts of “rotation”, “mirror image »And the method of comparison of the form of color configurations of indicators.
Part 3
Foreword
One key can open only one door. C. Shannon
Recently, marked by the loud triumph of the industrial introduction of artificial neural networks. Find out whether a word or a person, choose a melody according to his mood are tasks that can be considered with confidence already solved. The media is full of now and then emerging headlines about creating artificial intelligence, and science fiction writers argue about whether a thought can spontaneously originate in such networks. But is success really so grandiose, after all, to distinguish between numbers does not mean to have an abstraction of numbers, but to skillfully draw up sentences does not mean to be able to determine their meaning.
Let's try to look at these problems from a slightly different angle. In nature there is one process well-founded by it — evolution: everything that cannot adapt usually dies out. It was the task of adaptation at a certain stage that caused the development in living beings of the ability to perceive the properties of the external world, and the need to respond promptly to changes in these properties encouraged the development of animals in the nervous system. Is it therefore worth trying to imagine which tasks and in which complicating sequence the developing animal intellect had to be solved, because then, having solved them, we may repeat the path of evolution and finally get closer to understanding the mechanisms of thinking. The second seemingly reasonable idea is to start designing machines capable of making an idea about something (the fact of the presence of a mirror-symmetric fragment in the picture, or that the labyrinth under study has a way out) try:
1) call it “something” in terms of the perception of the machine;
2) to characterize the class of all those concepts that can be represented by the machine of this design.
However, to call what such basic concepts as “time” and “space” are, not within the framework of any formal theory, but by its nature, may turn out to be an insoluble problem. Here it is saved that in many cases the process of perception can be formally replaced by a (multi) character sequence depicting the states of the receptors at equal, rather short intervals of time. After such a substitution, the true nature of the concepts to be perceived is no longer important - only what they are in terms of the said symbol sequence is important. From this new position it is interesting to consider such concepts as “time”, “place”, “number”, “memory”, “future”. In this part of my work, I tried to find an approach to the definition of the concept of symmetry and the concept of form, as well as to show how they are actually implemented with the example of a “visual probe”. If you have not read the first part of the article , I recommend that you do this, because the parts are not independent and the further content may not be clear.
Inner definition of symmetries
Mathematics knows many examples when certain properties cannot be established "from the inside." Perhaps the most famous of them is the statement that it is impossible to establish its consistency only by means of arithmetic. The other says that it is impossible to describe it in any language, which of its phrases are truths in order not to miss anything and not to come but to a contradiction. In general, self-determination and self-descriptiveness are frequent causes of various paradoxes and antimonies. I wonder what a probe can “say” about itself? It is meant what qualities and properties of the probe a person can make up only on the basis of the experience of observing his indicators. For example, looking at the probe at least once, as on an object, it is difficult not to notice its symmetry. But can the probe itself "notice" it, because it has no way to "see itself"? Quite unexpectedly, it turns out that it is possible to form an idea of all the symmetries of the probe solely by the patterns of change in the color of cells perceived by its receptors. The method by which this can be done is devoted to the nearest story.
To begin with, we will find for everyone involved in the further description of the probe the concept of its “indicator double”. Methods for coloring seven cells surveyed by a probe are called color configurations. Since the probe can appear in different positions over the same cells (say, if there are turns among its simple movements), then, to be more precise, by the color configuration we mean a comprehensive description of what color each of its color-sensitive receptors is . Different color configurations are shown in Figure 15.
')

The dual concept of a color configuration is an understanding of a color configuration in an improper sense — an exhaustive description of which color indicators of the probe are on and which are not.
Since, by assumption, a simple movement occurs exactly when the color indicator that represents it goes out, these phenomena turn out to be dual to each other, and it is reasonable to call the latter a simple movement in an improper sense. A series of consecutive simple motions is called a general or composite motion. Any simple movement, as a series of length 1, is, with such a definition, including a general one. The phenomenon consisting in the fact that first only the ∆_1 lamp goes out, then only the ∆_2 lamp, ..., then only the ∆_n lamp and then between these moments not a single motion indicator is dual to the general movement, will be dual to the general movement.
This phenomenon Σ, depicted as ∆_1 * ∆_2 * ... * ∆_n, by virtue of the definition of simple motion in an improper sense, turns out to be a general motion in an improper sense.
It is easy to see that if Σ_1, Σ_2, ... Σ_k are common movements (in their own or improper sense), then the general movement will be the phenomenon Σ_1 * Σ_2 * ... * Σ_k, when Σ_1 first occurs, then Σ_2, ..., then Σ_k, and there are no movements between two of these movements following one another.
Some complex movements (in the proper sense) actually, in their completion, leave the probe in the same place in the same position. Therefore, they should be called stationary. Those, for example, are ↑ * ↓, ↖ * ↗ * ↓ and ↷ * ↶. Is it possible to determine the dual property of stationarity with respect to general movements in an improper sense? Direct translation of the formulation of this property would require a preliminary definition in terms of indicators of the concepts “place on the hexagonal lattice” and “probe position”, which we do not yet have. Let's try to find an indirect path. We note first that every time the color configuration observed before performing any stationary movement is exactly the same as after its completion. In this sense, all stationary movements "retain" color configurations. In fact, if the hexagonal grid is colored quite diverse, there are no other movements that preserve color configurations. These two circumstances speak of the equivalence of the properties “stationarity” and “movement to preserve color configurations”, the last of which is easily translated into the language of indicators: it is only necessary to perceive the terms “movement” and “color configuration” in an improper sense. The equivalence mentioned above gives us the right to consider this translation as a property dual to the property of stationarity. To express the stationarity property of the motion Σ (in proper or improper sense), we will use the formal notation Σ ≃E.
The movements of U and V such that their sequential execution in any order is a stationary movement (U * V≃E and V * U≃E), it is reasonable to call them reciprocal. Such are, for example, the pairs ↑ and ↓, and, ↷and ↶, (↖ * ↗) and ↓ among proper motions, as well as n [↑] and n [↓], n [↖] and n [↘], n [↷] and n [↶], (n [↖] * n [↗]) and n [↓] are among the improper ones.
Is it possible to extend the application of the “≃” equivalence sign to non-stationary motions? Thus, the general motion of ↑ and (↖ * ↗), being different in the method of implementation, in fact, leads to the same result. In general, if two instructions for the result of their execution, give the same movement of the probe, this fact can always be established by the form of these instructions. For example, wherever the probe is, executing either: “shift ↑, shift, then”, or: “shift ↖, then ↷, shift ↑” will change its position and position in the same way. “Equivalence” of two types of movements can be noticed also by direct observation of their implementation by the probe on the hexagonal lattice: in both cases it is enough to describe the final position in terms of initial, (for example, “after each U movement is completed, the probe is shifted by seven cells in the direction of "4", one cell in the direction of "6" and rotated 60 ° counterclockwise, counting from its position at the time of the start of this movement "). If the descriptions are the same, then the types are "equivalent." Nevertheless, there seems to be no simple way to establish the “equivalence” of movements in observing only the probe indicators. Here, the situation vaguely resembles the following: suppose there are many two-door wardrobes, behind each door of which there is a camomile or tulip hiding, and the flowers inside the same wardrobe are always the same: either are both daisies or tulips (Figure 16).

But is it possible to guess this pattern, if only one door can be opened in each cabinet? Watching the indicators it is difficult to understand that any two movements (in an improper sense) would always lead to the same changes in color configurations. Indeed, in reality, only one of these movements is performed each time. The impossibility of a simple definition of "equivalence" makes it somewhat difficult to use conventional algebraic methods in constructing a "probe theory" and forces us to use a strongly curtailed analogue of equivalence - stationarity. However, several useful rules of algebraic character can still be expressed:
i) Let U and V be stationary motions, then the motions of U * V and V * U will also be stationary;
ii) Let U * V be stationary motions, then whatever the stationary motion Σ, the motion U * Σ * V is also stationary.
The proof of the above rules, when all the terms are understood in the proper sense, follows from the definition of stationarity - the properties of movements ultimately do not change the position of the probe, and due to the duality principle, these rules are also true in the improper case. In the same way, by proving any statement about the projective plane, you can, by virtue of the duality principle of projective geometry, be considered proven and the statement obtained from the proven by replacing the words “point” with “straight line” and “direct” with “point”. An example of one more important property for describing a probe, generalizing the property of mutual reversibility, is demonstrated by a triple of motions - ↖, ↗, ↓. We agree to say that the motions of U, V, and W form a cyclic triple if their execution in any order leads to stationary motion. A simple analysis shows that among the elementary displacements there are exactly two cyclic triples: (, ↗, ↓) and (↙, ↘, ↑), which are obtained from each other by replacing their constituent motions with the reverse ones. It has already been shown how, observing the indicators, to select among them six light bulbs representing elementary displacements, but no actual way is given to indicate which of these light bulbs represents, say, the displacement, but which. Looking ahead, we warn the reader that there is simply no such way, due to the symmetry of the probe and the arbitrariness of its connection with the dial, but the dual nature of the cyclical properties and reciprocal reversibility makes it possible in the six lamps to indicate pairs corresponding to pairs of reciprocal movements, and triples corresponding to cyclic triples. For simplicity, we will talk about reciprocal indicators and their cyclic triples. It turns out that these two properties are quite enough to express in dual terms the concept of symmetry of the probe as an object. A probe as an object can be “superimposed upon itself”, turning it over like a coin, or turned around a central receptor. Any such “overlay” defines a permutation between the marks “12”, “2”, “4”, ..., “10” of the dial associated with it. For example, when turning by 60 degrees in the clockwise direction, "12" is superimposed on "2", "2" - on "4", ..., "10" - on "12". This permutation in view of the accepted correspondence between dial marks and elementary displacements generates a permutation: "↑" → "↗" → "↘" → "↓" → "↙" → "↖" → "↑". The latter, as can be seen in Figure 17, retains the properties of cyclicity and mutual reversibility in the sense that if the two displacements are reciprocal, then they are translated into reciprocal, and if some three of them form a cyclic triple, then their images also form a cyclic triple .

In fact, the described situation with preservation of cyclicity and mutual reversibility is not accidental: the numbers corresponding to reciprocal movements are diametrically opposed to the dial of the ball, the corresponding cyclic triples are located at the ends of the correct three-pointed "stars" (Fig. 18), and any overlap of the probe on itself certainly retains the diametrical opposite of its points and the shape of the “stars”.

By simple reasoning, it can be shown that the opposite: every permutation among elementary displacements that preserves the property of mutual reversibility and cyclicity is generated exactly by one imposition of the probe on itself.
The set of all such permutations is called the group of internal symmetries of the probe. This name is justified by the following fact. Give some names to all the color indicators (we denote the set of names involved in this case by K) and all the indicators representing elementary displacements (we denote the corresponding set by M). A sufficiently detailed description of the probe (as a system of patterns of indicator states) will be a list L of all such triples of names x, y, p, for which the indicator of color x lies in the direction of the elementary displacement represented by indicator p from the indicator of color y (in an improper sense). Let m be the permutation of the names of the color indicators on M, and k the permutation of the names of the indicators representing the elementary displacements on K. What if we perform these permutations simultaneously within the list L? Generally speaking, both the look of the list and the meaning that it contains can change after that. However, if k and m are generated by some superposition of the probe on themselves, then the only result of the mutual implementation of these permutations in the list will be a change in the order of enumeration of triples, which does not affect its meaning.
Suppose now that some m and k after their execution on the list L change in it, except that only the order of the triples, it turns out that the opposite is true: they must be generated by some imposition of the probe on themselves (as an object), and all such m form an isomorphic group internal symmetry of the probe. In more detail about the connection of symmetries of an object with the symmetries of its descriptions will be discussed in the next chapter.
Shape perception mechanisms
How to define the concept of form? Let's imagine how his children comprehend. Take, for example, the educational game for the smallest ones - a wooden puzzle is a set of objects of different geometric shapes and a board with holes suitable for the shapes of objects. A child solves a difficult task for himself: what form should an object be, so that it can be inserted into a hole. The first success in this game is waiting for him with a round-shaped element - it is symmetrical about turns and is easily recognizable. But with the element of the puzzle in the form of a box, accidentally turning it over, the child will have to tinker pretty.

Watching birds, especially ravens and parrots, is easy to see, as they look at objects, they tilt their heads to the right, then to the left. It is known that many living creatures (including more simple than the crows) are able to recognize objects in their mirror image, whereas you can see the reflected object in its reference position only by changing the eyes and turning the retina in them.
The concept of the form of things does not apply only to visual perception: people easily recognize favorite tunes, even if you play these tunes a little differently than in the original: an octave higher or lower, in slow motion or in an accelerated one; even if the melody is whistled, you can still recognize it. Is music therefore a form of a sequence of sounds?
It turns out that often the form or symmetry of a thing can be judged only by its description. This method is preferable in that it does not require any manipulations with the thing itself and, perhaps, it allows one to recognize the melodies without being able to slow down or speed up the time or change the octave of the sound, and the shape of the objects without tilting the head or pushing them through the holes.
Things themselves, both real and mathematical abstractions, in most cases are collections of simpler things that are in certain relationships with each other: a brick wall is a collection of bricks arranged in a certain way relative to each other, a work team is a collection of people connected by relations subordination.
As another example, we will consider an arbitrary triangle, as a set of three segments with the relations “have length” and “have a common end”.

In these terms, the equilateral triangle in Figure 20 admits the following comprehensive description:
“The triangle ∆ is the set of three segments a, b, c, and:
1) one of the ends of a is common with b, the other with c, the length of a is 5;
2) one of the ends of b- is common with c, the other is from a, length b is 5;
3) one of the ends of c is common with a, the other with b, length c is equal to 5
".
It is difficult not to notice the surprising symmetry of this description, which to some extent reflects in itself all the symmetries of the triangle it defines. To give the above, greater clarity, we impose a triangle on ourselves, turning 120 degrees (Fig. 21).

Upon completion of this movement, a will move “to the place” b, b - “to the place” c, c in turn - “to the place” a. If we formally carry out the written permutation in the description of ∆, we get the following:
“The triangle ∆ is the set of three segments a, b, c, and:
1) one of the ends b is common with c, the other with a, length b is 5;
2) one of the ends of c is common with a, the other with b, length c is equal to 5
3) one of the ends of a is common with b, the other with c, length a is equal to 5
".
This shows that as a result of this substitution, the description of ∆, with the exception of an insignificant change in the order of transfer, completely preserves its form. As the reader may guess, the reverse is also true: any permutation among a, b, c, preserving, with the mentioned reservation, the type of description ∆, is generated by some of its geometric symmetry.
Such a duality between the symmetries of a thing and the symmetries of its description does not always occur. Of course, if the description already has some symmetry (there is a permutation of the names of things appearing inside the description that do not change its appearance), then it is necessarily generated by the symmetry of the thing. The reverse, however, is not true: the same one-sided triangle can be given a description that does not have any symmetries except the identical one:
“The triangle ∆ is the set of three segments a, b, c, and:
1) one of the ends of a is common with b, the other with c;
2) one of the ends b is common with c, the other with a;
3) one of the ends of c is common with a, the other with b;
4) length a is equal to 5;
5) the angle between a and b is 60 °;
6) the angle between b and c is 60 °. "

Let us pay attention now to the case when the thing is a graph. Each graph can be considered as a collection of vertices with a two-place relation “... connected by an edge with ...”, and to get an exhaustive description of a particular graph, it is sufficient to simply list all the pairs of its vertices that are in this respect. We describe this description as a list of incidents. For clarity, the vertices of the graph can be imagined as buttons, and the edges connecting them - threads.
Any overlay (mapping a set of vertices of a graph onto itself), in which exactly one vertex is superimposed on each vertex and exactly one edge on each edge, is naturally called the symmetry of this graph, if overlapping with the listed conditions is possible between two different graphs, it is natural to talk about isomorphism between graphs of the same form .
Let the reader be an easy exercise to show that every symmetry of a graph corresponds (dually) to some symmetry of its list of incidents, and two graphs have the same form if and only if the list of incidents of one can be obtained from the list of incidents of the other by simply replacing (exact substitution) vertices in this list.
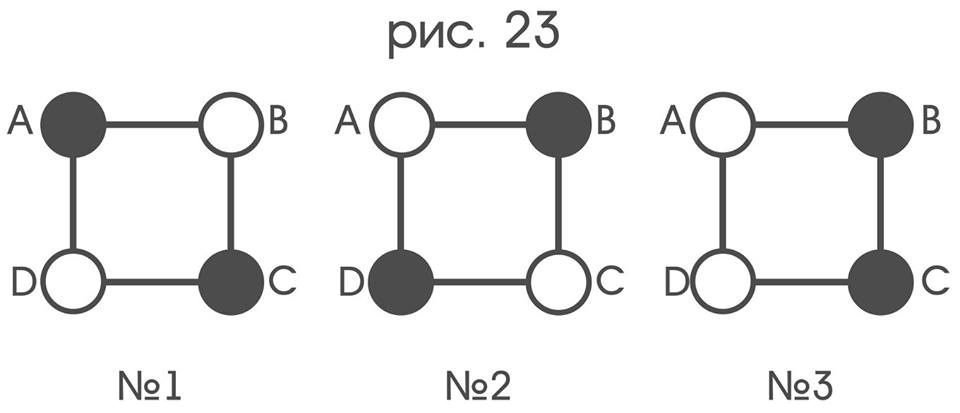
Figure 23 shows three differently colored instances of the same graph.

Probably the most immediate way to get a description of an instance of a graph with a selected coloring is to add to the list of its incidents an enumeration of what color each of its vertices has. It is obvious that not all symmetries, exactly as not all graph isomorphisms, leave the chosen coloring unchanged: since when you try to impose the specimen No. 1 on yourself by turning 90 °, each vertex will be applied to the vertex of the opposite color. Therefore, it is reasonable that the symmetries of a colored graph, in which only vertices of the same color overlap, are called the symmetries of the chosen coloring, and if an isomorphism with the described property is possible between two graphs, then talk about the isomorphism between the coloring of two graphs of the same form (or about the same with accuracy before this form isomorphism coloring).According to these definitions, the coloring of copies No. 1 and No. 2 have the same shape, which differs from the coloring form of copy No. 3.
But what to do if there is no physical way to overlay some columns on others? How then to determine the shape of the coloring? Let again for the reader it will be a simple exercise to show that any symmetry of the selected coloring of the graph corresponds (dual) to such a permutation of the names of its vertices, which preserves both the list of incidents and the list of colors of the vertices. Colorings of two different graphs have the same form if and only if both mentioned lists for one of them can be obtained from the lists for the other by a simple substitution (exact substitution) of the names of their vertices.
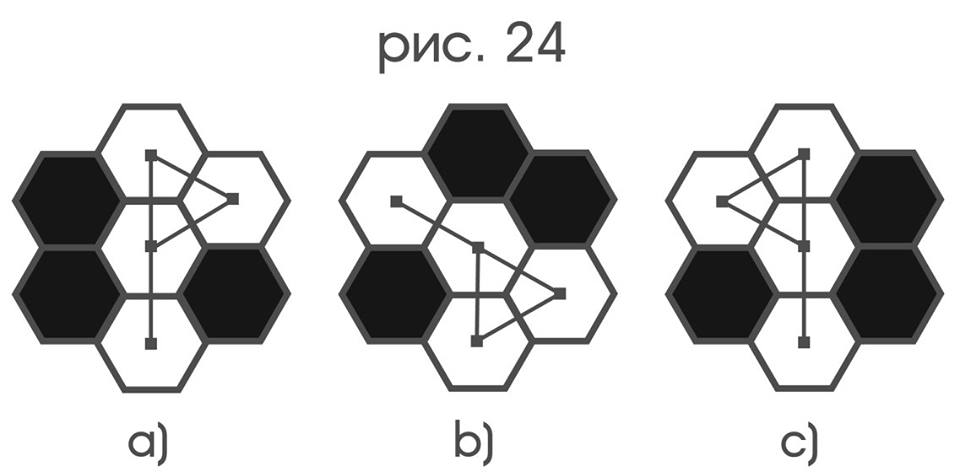
Now it is time to shed some light on how the shape comparison of objects takes place. The most convenient way to do this is using the example of a probe already familiar to us, and the consideration will touch the extreme case of the constraint of its simple movements, when the latter are limited exclusively by elementary displacements. It turns out that it is already enough of them to say with respect to the color configurations of the lattice cells in Fig. 24 that the flags a) and b)

one form up to “rotation”, flags b) and c) one form up to “specular reflection”, while the probe itself, I emphasize once more, is deprived of any opportunity to turn or “mirror reflect”. In the described situation, the concepts of “rotation” and “mirror reflection” will receive correct definitions by purely linguistic methods. In many ways, all of the above is possible due to the remarkable fact that, like the lattice area in the “field of view of the probe,” the probe itself has exactly the same set of symmetries that the “umbrella” graph of Figure 25 has.

In order to give the promised way of comparing the forms of color spots, it will be shown how to enter a structure that turns each of these sets into an umbrella graph on a set of cells under a probe, a set of color sensory receptors and a set of receptor-related indicator indicators. Thus, the task of comparing the forms of color spots will be equivalent to the problem of comparing the forms of coloring of an umbrella graph.
The idea of solving the latter without involving geometrical concepts that are not yet defined in a vicious circle is to judge the symmetries of the umbrella graph by the symmetries of its description. But this is where the problem arises: which of these symmetries should be called reflections, and which turns (the umbrella graph does not have other symmetries), because without realizing the direct manipulation of the thing, the meaning of the words “reflection” and “rotation” is lost, while Description when performing permutations of names in it does not rotate or reflect?
One of the ways to return the lost meaning is to find the categorical property of the permutations corresponding to each specific type of symmetry. The orbit structure is a suitable and proven property for this purpose. So symmetry, in the intuitive understanding of which is a rotation of 60 °, corresponds to a permutation

and only turns of 60 ° have the structure of orbits π :

Symmetries, in the intuitive understanding of which are mirror reflections, and only they have structure I :

The structure of orbits E :
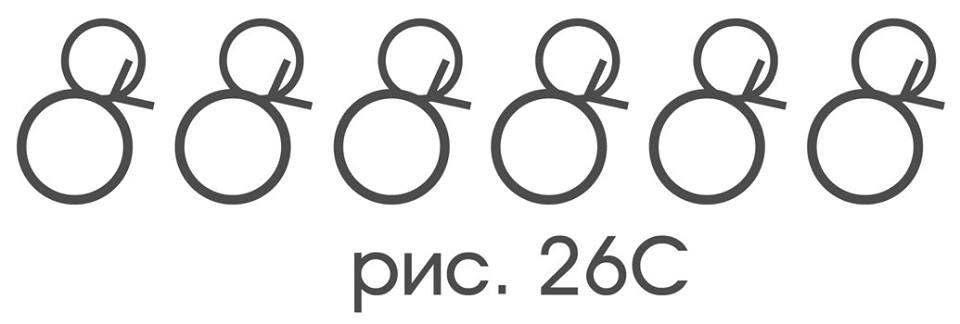
only identical symmetry,
the structure

is only a 180 ° rotation,
and only “a 120 ° rotation” unambiguously corresponds to the structure:

This completes the enumeration of all possible types of symmetries of the umbrella graph.
Let's transform the lattice region, which is the “field of view” of the probe, into a graph, the vertices of which are the cells of this region, and the edges between them represent the relation “to be adjacent on the side” (Fig. 27).

Such a metamorphosis makes it possible to compare the images viewed by the probe, as the coloring of the resulting graph, by analyzing their descriptions, without requiring any "physical" possibility to impose something on each other. For example, the color configurations in Fig. 24 correspond to the coloring of a '), b'), c ') of the umbrella graph (Fig. 28), moreover, if under the “rotation”

and “mirror reflection” to understand that the orbits have permutations that correspond to isomorphisms of colorings of a particular structure, then a ') and b') really have the same shape with an accuracy of 120 °, and b ') and c') with accuracy before mirroring.
The reader probably drew attention to the fact that from the very beginning the probe was depicted in the form of an umbrella graph with receptors-tops and rigid rods-ribs. One could therefore say that comparing the shape of color configurations on its receptors again comes down to analyzing the descriptions of the colorings of the above graph, however, hard rods cannot be seen with the help of receptors or make a picture of them from observing the indicators. However, there is still a way to turn multiple receptors into a perceptible umbrella graph with the same structure: all you need to do is note that the x receptor is “connected by a rod” with the y receptor exactly when the relationship is:
“There is an elementary displacement of S such that x lies in the direction of S from y”. It is in this place that the presence of all elementary displacements among the simple movements of the probe is important, since then the justice or the injustice of the latter by the relationship between specific x and y receptors can be established by sufficiently long observation of the colors perceived by them. Another observation is that elementary displacements among simple movements are sufficient to judge the uniformity of form and two configurations obtained from each other by turning or mirroring, even when the probe itself cannot in principle be rotated or mirrored.
It remains to note that the phrase “∃ S (S is an elementary displacement) (x lies in the direction S from y)” allows direct translation into dual terms, thereby defining the dual relation on the set of color indicators, which turns this set into an umbrella graph. The latter means that only by observing the bouquets of lamps associated with the probe, even when all its simple movements are reduced to plane-parallel displacements and the probe itself is not directly observable, it is still possible to adequately and exclusively in internal terms define the concepts of “rotation”, “mirror image »And the method of comparison of the form of color configurations of indicators.
Source: https://habr.com/ru/post/282327/
All Articles