Parsing final tasks Technokubka 2016
Mail.Ru Group together with MIPT and MGTU im. N. E. Bauman summed up Technokubka - the first programming contest for students of 8-11 grades. Schoolchildren from more than 20 cities in Russia and the CIS fought for the title of the most talented young programmer. A total of 2132 participants registered for the Olympiad, 113 came to the internal finals, which took place simultaneously at two venues: at Moscow State Technical University. N. E. Bauman and MIPT. The award ceremony took place at the Mail.Ru Group office. The Olympiad was held on the Codeforces platform.
The guys had three hours to solve the seven tasks that were made by teachers and specialists from leading technical universities of Russia. The last, the most difficult, was decided only by one of the participants - Vladislav Makeev, who eventually won first place. In total, 27 participants of the Olympiad became winners, they shared diplomas of the I, II and III degrees. The winners (diploma of I degree) received an additional eight points for admission, holders of diplomas of II and III degree - six points each. The first place was taken by Vladislav Makeev (Moscow, 11th class), the second - Aleksandra Drozdova (Nizhny Novgorod, 10th class), the third - Grigory Reznikov (Moscow, 11th class). The full list of winners is available here . In this post, we suggest that you familiarize yourself with the tasks of the final and their solutions.
')
Idea: Mikhail Mirzayanov, SSU
Development: Alexander Frolov, SSU
Subject: modeling
Vasily dreams of becoming a k- th programmer. He has n days to fulfill his plans - to raise his level from the 1st to the kth . To move from level x to level x + 1, it is necessary to solve x problems from the moment x is obtained.
On the i- th day, a i tasks are published on one well-known website, and all of them are available for solving only on the day of publication. Every day Vasily solves problems one after another, and on the i- th day he can solve no more than a i tasks. As soon as the total number of problems solved by Vasiliy since the last level x was received, becomes equal to x , he stops and does not solve more problems on this day. In this case, at the end of the day he makes the transition to the next level x + 1. At the same time, the tasks that Vasily did not have time to solve this day, he will not solve it ever.
The solved tasks do not accumulate during the transition to the next level, that is, for each x, to go to level x + 1, Vasily needs to solve x problems, being a programmer of level x .
Vasily can start classes any day from 1 to n , while he wants to minimize the difference between the number of the day when he becomes a programmer of level k and the day when he begins to study.
Input data
The first line of input data contains two integers n and k (1 ≤ n ≤ 500, 2 ≤ k ≤ n + 1) - the total number of days and the level that Vasily wants to achieve, respectively.
The second line contains n integers a 1 , a 2 , ..., a n (1 ≤ a i ≤ 500), where a i is equal to the number of tasks available on the i- th day.
Output
Print a single integer - the minimum number of days during which Vasily will be able to achieve the k -th level of programming.
If Vasily cannot achieve the desired, output -1.
To begin with, we note that in the process of solving problems it is never beneficial to take breaks, since the excess tasks remaining on a given day can simply not be used.
Thus, the only thing that makes sense to change is the day the pumping starts. We will enumerate all possible variants of the first day and simulate the programmer’s build process for each one. The complexity of this solution is O (n 2 ) , since the possible variants of the starting day n and for each day are simulated during the time O (n) .
Authors of the idea: Gleb Evstropov, HSE, and Mikhail Mirzayanov, SSU
Development: Alexander Frolov, SSU
Topics: Hamming distance, counting
Ivan loves to read newspapers; he is especially interested in political and sports news. Ivan also has a favorite string s .
Ivan has a lot of free time, and he reads very quickly, but there are not so many newspapers that interest him. Therefore, recently, after reading a regular newspaper, Ivan began to consider the number of occurrences of his favorite string s in the text t written in the newspaper as a substring. A substring of the string x is a sequence of consecutive characters of the string x .
But soon, and with counting the occurrences, Ivan began to cope very quickly, and after reading the next newspaper he decided to replace in his favorite line no more than k characters so as to maximize the number of occurrences of the modified line s in the text of the newspaper t .
Your task is to help Ivan and count the maximum number of occurrences of his favorite string s after replacing no more than k characters in it in the text of the newspaper t . Ivan does not have to replace exactly k letters, and he may not even have to replace a single letter. You can replace the letter from the string s with any other.
Input data
The first input line contains three integers n , m and k (1 ≤ n ≤ m ≤ 250, 0 ≤ k ≤ n ) - the length of the string s , the length of the string t and the number of characters that Ivan can replace in his favorite string, respectively.
The second line of input should be a non-empty string s , consisting of n lowercase English letters - Ivan’s favorite string.
The third line of the input data is followed by a non-empty string t consisting of m lowercase English letters - text written in a newspaper. It is guaranteed that the length of string s does not exceed the length of string t .
Output
Output a single integer - the maximum number of occurrences of Ivan’s favorite string s after replacing no more than k characters in it in the text of the newspaper t .
A naive solution that goes through all the options for changing the original string s and considers the answer for them has exponential complexity. However, we note that there are no more different variants having at least one occurrence than | t | - | s | + 1, that is, the number of ways to "attach" the string s to the string t .
We change the order of calculations, iterate all possible positions of the application of the string s to the string t, and for each we calculate exactly which positions and which characters need to be changed to get an entry in this position (or we can determine that it is impossible to keep within k changes). It is required in some way to code the necessary changes in order to be able to distinguish whether the line requires identical changes for two different positions of the application or different ones. In this problem there were small restrictions on the length of the strings t and s , therefore it was allowed to use almost any polynomial solution. For example, the necessary changes could simply be represented by an array of length | s |.
Now select the groups of the same changes and find the group of the same size. This can be done in many different ways, for example using sorting or hashes.
Author of the idea and development: Alexey Dmitriev, MIPT
Subject: Math
HackerCook company has its grand championship in sports programming with a large prize fund, but the distribution of prize money has not yet been announced. The only thing that is known about the final distribution is that a participant with a higher place will receive no less prize money than a participant with a lower place.
Now, one HackerCook employee wants to distribute the prize fund so that his friends receive a sum of money as much as possible. Determine what part of the prize fund each participant will receive, provided that the employee distributes the money optimally.
Input data
The first line of the input data contains two integers n and k (1 ≤ k ≤ n ≤ 1 000 000) - the total number of participants and the number of friends of the Hacker Cook employee.
The second line contains k different integers a i (1 ≤ a i ≤ n ) in ascending order — the places that were occupied by the friends of the cunning developer.
Output
Print n non-negative integers b 1 , b 2 , ..., b n (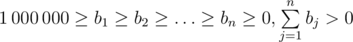
), which means that the participant who took the i- th place must receive 
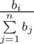part of the prize pool.
If there are several possible answers, you can print any.
It is guaranteed that there is an optimal answer satisfying the condition described in the output format.
Briefly: consider all the options to distribute all the money equally between the first few participants, at least one of these options will be the best answer.
How to prove it? Consider some optimal answer. Let there be some two participants A and B receive a different positive amount of money, let us denote their earnings by a and b (then 0 < a < b ). We divide all participants with a positive amount of money into those who received at least b , and those who received less b . Let in these groups X and Y participants, respectively, and among them x and y friends, respectively (at least one of the numbers x and y is positive).
Suppose we chose the number k and increase the earnings of each participant in the first group by k / X , and in the second group decrease by k / Y (note that the total amount is saved). Then the earnings of friends change to k (x / X - y / Y) . Note that we can pick up both positive and negative k in such a way that after a change no participant gets more money than those who are higher than him, and all earnings are non-negative. Since our answer is optimal, x / X = y / Y (otherwise, by choosing the number k of the desired sign, we could improve it). Choose k such that in the second group one of the participants has 0 money. The number of participants with a positive gain has decreased; we will repeat this process until all participants with a positive amount of gain do not equal.
Technically, the task is very simple: among all the prefixes of the sequence, you must choose such that the share of friends in it is maximum. This is done by a simple linear approach and saving the current answer as a fraction a / b .
Author of the idea and development: Mikhail Mirzayanov, SSU
Topics: greed, event handling
Vasya wants to give Masha a bouquet on March 8. He knows one secret path in the woods outside the city, along which grow beautiful, and most importantly, free flowers. The path can be represented as a straight line, and we can assume that Vasya initially appears on it at point 0 and moves at a speed of 1, without taking the time to pick flowers.
Flower number i grows at the point of the path with the coordinate x i , and after Vasya breaks it, the flower remains alive t i units of time. Naturally, Vasya should dial an odd number of flowers into a bouquet, and they should all be alive at the moment when he brings them to point 0 to meet Masha (if the i -th flower is brought exactly t i units of time after it is torn off, then no longer considered alive).
Vasya is a straight line man, and even for the sake of Masha he is not ready to turn (that is, change the direction of his movement along the path) more than twice. Help him collect the largest bouquet of odd size.
Input data
The first line of the input data contains a single integer n (1 ≤ n ≤ 200 000) - the number of flowers growing along the path.
Each of the following n lines contains two integers x i and t i (–10 9 ≤ x i ≤ 10 9 , 0 ≤ t i ≤ 10 9 ) - the coordinate of the i -th flower and the time it will be alive after he'll be ripped off, respectively. At one point can grow more than one flower.
Output
Print a single number - the maximum possible number of flowers in a bouquet. If it is impossible to collect a bouquet from even one flower, output 0.
The condition that Vasya is ready to change the direction of movement no more than twice clearly defines the form of the answer: first we go to one of the two sides until it stops, then, returning, we collect all the flowers, go through 0 and go the other way until some moment , then again we turn around and go to 0, again collecting all the flowers in its path. From how far we go from point 0 before the last turn, it depends, on the one hand, how many flowers we can collect on the way back, and on the other, how many flowers collected in the first section will have time to wither.
Without loss of generality, we will assume that we first went from point 0 to the left (negative coordinates), and then to the right. Then “turn the world” and solve a symmetric problem. Of course, we will collect a bouquet of the maximum size, and then we simply find the odd number nearest to this maximum.
A flower to the right of point 0 can be delivered to Masha if x i < t i for the corresponding i . Let us go to the right from point 0 to coordinate R. Then the flower i , located to the left of point 0, can be delivered to Masha uncomfortable if t i + x i - 2 R > 0 or R <( t i + x i ) / 2. Thus, n events are located along the ray with positive coordinates, each of which either adds a new flower or removes it. Go from 0 to the coordinates of the maximum event and find the maximum positive balance. It should carefully handle events located at one point and between integer points (here the problem will be solved by multiplying all coordinates by 2).
Author of the idea and development: Alexander Ostanin, MIPT
Topics: Mathematics, Graphs
In the championship of the Berland Hockey League n teams participate. The tournament is held in a round robin: each team plays exactly one match with each, and there are no draws in the tournament. Unlike traditional tournaments, the distribution of prizes in the Berland Hockey League does not depend on the final place of the team, but on the number of victories. Namely: all teams that have won at least w games receive prizes. Hockey expert Don Berry wonders if, based on the results of this tournament, exactly k teams will receive prizes. If such a tournament exists, you need to display a winner for each match.
Input data
The only input line contains three numbers n , w and k (2 ≤ n ≤ 1000, 0 ≤ w ≤ n , 0 ≤ k ≤ n ) - the number of participating teams, the minimum number of wins for receiving the prize and the number of winners of the tournament, predicted by the expert .
Output
If a tournament with such properties does not exist, output "NO" (without quotes) in the only line of the output.
Otherwise, in the first line print "YES" (without quotes). Then output n lines of length n , j -th character of the i- th of them should match the match between teams i and j . If i = j , then the corresponding symbol must be equal to 0. If the i team defeated the j command, then this symbol is 1, otherwise 0. For all i ≠ j, exactly one of the two symbols corresponding to the meeting of these teams must be equal to 1.
We will solve a more difficult task: we will construct such a tournament, that the minimum of points among the first k teams is as large as possible, and the maximum points among the last n - k teams are as small as possible (it is stated that in some tournament the optimal values of these values are reached simultaneously). Then either this tournament is the answer, or there is no answer.
It is obvious that in the optimal tournament each of the first k teams must win each of the last n - k , it remains to decide how all the first teams will play each other and how all the last teams will play. We would like to see as many points as possible in the microtournament among the first k teams, and as many points as possible in the last teams tournament.
Let m teams participate in a tournament and m is odd. Then, in a complete graph on m vertices, all the degrees of the vertices are even, which means that there exists an Euler cycle in it (and it can be constructed in O (m 2 ) time ). If we orient the edges along the cycle and say that the edge leads from the winning team to the loser, we get a tournament in which each team won exactly (m-1) / 2 times.
Now suppose that m is even. Then it is impossible to build a tournament with the same number of points for all teams and the last team will have no more (m-2) / 2 points. But a tournament with such a property can be built if you throw out one vertex, apply the algorithm from the previous paragraph to the remaining m - 1 teams, and then put extra team wins in half of the remaining teams. In the resulting tournament, half the teams (m-2) / 2 points, and the other half - m / 2 points.
This way of building the most “even” tournament is suitable both for the first k teams and for the last n - k teams. In the end, we check that it really is the answer (that is, all the first teams won at least w times, and the rest won less than w times).
Authors of the idea and development: Gleb Evstropov, HSE, and Mikhail Mirzayanov, SSU
Topics: greed, dynamic programming
Twenty years have passed. Carlson is stout and no longer flies. The kid got a job, became a top manager and now lives in a huge house on the n- th floor.
Carlson decided to go on a visit to the Kid. Of course, he is not going to go up on foot, so on the first floor Carlson enters the elevator.
Buttons in the elevator are located from bottom to top in such a way that a person with an increase in h can reach any button corresponding to the floor from 1 to h inclusive. At the same time, on the i- th floor, Carlson has a friend with an increase in h i , and he can be asked to press any button he can reach. Of course, to ask a friend from the i- th floor to press a button, you first need to be on floor i . Carlson wants to get to the Kid, turning for help to the minimum possible number of friends.
Unfortunately, over time, Carlson's character also deteriorated, so sometimes he quarrels with his friends, but not more than one friend at a time. For each i, Carlson wants to determine the minimum number of friends to whom he will have to ask for help if he quarrels with his friend number i and cannot address him with a request to press a button.
Input data
The first line of the input data contains two integers n and h (2 ≤ n ≤ 10 6 , 1 ≤ h ≤ 10 9 ) - the number of the floor on which the Kid lives and the height of Carlson, respectively. The next line contains integers h 1 , h 2 , ..., h n - 1 (1 ≤ h i ≤ 10 9 ), the i -th of which corresponds to the height of a friend of Carlson living on the i- th floor.
Output
Output n - 1 number of ans 1 , ans 2 , ..., ans n - 1 , where ans i is equal to the minimum number of friends you have to ask for help if Carlson quarrels with a friend living on the i- th floor. If, having quarreled with his i -th friend, Carlson cannot get to the Kid, then output -1 instead of the corresponding value of ans i .
First, we solve the problem under the condition that Carlson is friends with all his friends. At any given time, we can assume that some prefix of floors is available to it, because if Carlson could get to floor x , he could get to all intermediate floors. Then, obviously, the most profitable move will take the help of the highest friend on this prefix. The complexity of this solution is O (n) .
This immediately gives us a way to solve the original problem in a quadratic time — to sort through which friends Carlson is quarreling with and solve the problem for each case. Now we will notice that on each prefix we are interested only in two maximum values, and we will count the following values:
f i - the minimum number of steps for which Carlson can get to Tiny if he has access to the prefix of floors 1 to i and at the same time he did not quarrel with the highest friend on this prefix;
g i is the minimum number of steps for which Carlson can get to Toddler if he has access to the prefix of floors 1 to i and he has quarreled with the highest friend on this prefix (and therefore, he will have to ask for the second highest friend).
We denote by a i the highest friend among the first i , and by b i - the second highest. Then f i = f ai + 1, and g i = g bi + 1, if a i = a bi , and g i = f bi + 1 otherwise.
Now let's learn how to calculate the answer using these values. If one of Carlson's friends did not initially enter into the optimal answer, then the answer for the case of a quarrel with this friend is equal to the optimal one. If it did, then the answer for this i would be k - 1 + g i , where k is the sequence number of this friend in the optimal answer.
Author of the idea and development: Konstantin Semenov, MIPT
Petya and Vasya play the famous game “Rock, Scissors, Paper”. The game takes place in n rounds. In each round, Petya and Vasya choose one of three figures: stone, scissors, or paper. If the figures of the players do not match, the winner is determined in the standard way (the stone defeats the scissors, the scissors defeats the paper, the paper defeats the stone), otherwise a draw is declared. For victory, w points are awarded, for a draw - d points, for defeat - 0 points. The total score of each player is the sum of points for all rounds.
Petya determined in advance which figure he would choose in each round, and wrote it down as a string of length n with the letters r , s, and p . Here, the letter r at the i -th position in the line means that in the i- th round, Petya will choose a stone, s - scissors, and p - paper.
Vasya got a certain cyclical shift of Petr's line and wants to use this information to maximize his final score. Find the maximum score that Vasya can guarantee himself no matter what kind of cyclic shift of the source line is the line known to Vasya.
Input data
The first line of input contains three integers n , w and d (1 ≤ n ≤ 100 000, 0 ≤ d ≤ w ≤ 10 9 ) - the number of rounds, the number of points for the victory and the number of points for a draw, respectively.
The second line contains a string of length n , consisting of the characters r, s, p , the cyclic shift of the line written by Petya.
Output
Output one number - the maximum score that Vasya can guarantee himself.
Suppose we have already seen the first few characters of Petina’s string and they make up the string t . Let f (t) denote the maximum bill that we can provide for ourselves; the answer to the original problem is f (empty string) . If the string length t is equal to n , the game is over and f (t) = 0.
Let t be less than n . If our next move is, for example, r (stone), in the worst case we will earn the minimum among the numbers: f (t + p) (the next Petin move is paper, we lost), d + f (t + r), w + f (t + s) . If any of these values is not defined (for example, if the string t + p is not a prefix of any cyclic shift), we set by definition f (t) = ∞. For the remaining two possible moves, the result in the worst case is calculated in the same way; since we can choose our next move, among the results for the three possible moves we choose the maximum, this maximum is equal to f (t) .
This method allows us to calculate the answer to the problem. All possible values of the string t , for which f (t) is not equal to infinity, are conveniently represented as a root tree, a boron, in which a letter is associated with each edge and a line is associated with any path from the root — a sequence of letters along which the path passes. The previous algorithm can be represented as dynamic programming on a tree in which all cyclic shifts of the source line are present. The tree size and complexity of the algorithm are O (n 2 ) .
To optimize, we need an advanced structure - a compressed suffix tree. We construct a boron, which contains all the suffixes of the string s , after which we “compress” into one edge a chain of vertices from which only one transition proceeds (now a line of some length is written on each edge). The resulting tree will contain O (| s |) vertices and edges; in addition, it can be constructed in linear time (for example, using the Ukkonen algorithm or using a suffix automaton).
Let's return to our task. If we calculate the value of f at the vertex, from which only one transition comes, we simply add w to the value of f for the only son of that vertex. This means that the method of calculating f is easily transferred to a “compressed” bur: when we go along an edge of length L, we add w ( L - 1) to the result.
Construct a compressed suffix tree for a doubled source line. This tree contains all the cyclic shifts of the original row, so it is possible to calculate the values of the function f from it , carefully examining cases where we go to the vertices at a depth greater than n . The final solution works in linear time.
If you are interested in such tasks, you can take part in the Russian Code Cup 2016 and compete for a cash prize!
The guys had three hours to solve the seven tasks that were made by teachers and specialists from leading technical universities of Russia. The last, the most difficult, was decided only by one of the participants - Vladislav Makeev, who eventually won first place. In total, 27 participants of the Olympiad became winners, they shared diplomas of the I, II and III degrees. The winners (diploma of I degree) received an additional eight points for admission, holders of diplomas of II and III degree - six points each. The first place was taken by Vladislav Makeev (Moscow, 11th class), the second - Aleksandra Drozdova (Nizhny Novgorod, 10th class), the third - Grigory Reznikov (Moscow, 11th class). The full list of winners is available here . In this post, we suggest that you familiarize yourself with the tasks of the final and their solutions.
')
Task A. Level 80 Programmer
Idea: Mikhail Mirzayanov, SSU
Development: Alexander Frolov, SSU
Subject: modeling
Condition
Vasily dreams of becoming a k- th programmer. He has n days to fulfill his plans - to raise his level from the 1st to the kth . To move from level x to level x + 1, it is necessary to solve x problems from the moment x is obtained.
On the i- th day, a i tasks are published on one well-known website, and all of them are available for solving only on the day of publication. Every day Vasily solves problems one after another, and on the i- th day he can solve no more than a i tasks. As soon as the total number of problems solved by Vasiliy since the last level x was received, becomes equal to x , he stops and does not solve more problems on this day. In this case, at the end of the day he makes the transition to the next level x + 1. At the same time, the tasks that Vasily did not have time to solve this day, he will not solve it ever.
The solved tasks do not accumulate during the transition to the next level, that is, for each x, to go to level x + 1, Vasily needs to solve x problems, being a programmer of level x .
Vasily can start classes any day from 1 to n , while he wants to minimize the difference between the number of the day when he becomes a programmer of level k and the day when he begins to study.
Input data
The first line of input data contains two integers n and k (1 ≤ n ≤ 500, 2 ≤ k ≤ n + 1) - the total number of days and the level that Vasily wants to achieve, respectively.
The second line contains n integers a 1 , a 2 , ..., a n (1 ≤ a i ≤ 500), where a i is equal to the number of tasks available on the i- th day.
Output
Print a single integer - the minimum number of days during which Vasily will be able to achieve the k -th level of programming.
If Vasily cannot achieve the desired, output -1.
Parsing
To begin with, we note that in the process of solving problems it is never beneficial to take breaks, since the excess tasks remaining on a given day can simply not be used.
Thus, the only thing that makes sense to change is the day the pumping starts. We will enumerate all possible variants of the first day and simulate the programmer’s build process for each one. The complexity of this solution is O (n 2 ) , since the possible variants of the starting day n and for each day are simulated during the time O (n) .
Task B. Replacing letters
Authors of the idea: Gleb Evstropov, HSE, and Mikhail Mirzayanov, SSU
Development: Alexander Frolov, SSU
Topics: Hamming distance, counting
Condition
Ivan loves to read newspapers; he is especially interested in political and sports news. Ivan also has a favorite string s .
Ivan has a lot of free time, and he reads very quickly, but there are not so many newspapers that interest him. Therefore, recently, after reading a regular newspaper, Ivan began to consider the number of occurrences of his favorite string s in the text t written in the newspaper as a substring. A substring of the string x is a sequence of consecutive characters of the string x .
But soon, and with counting the occurrences, Ivan began to cope very quickly, and after reading the next newspaper he decided to replace in his favorite line no more than k characters so as to maximize the number of occurrences of the modified line s in the text of the newspaper t .
Your task is to help Ivan and count the maximum number of occurrences of his favorite string s after replacing no more than k characters in it in the text of the newspaper t . Ivan does not have to replace exactly k letters, and he may not even have to replace a single letter. You can replace the letter from the string s with any other.
Input data
The first input line contains three integers n , m and k (1 ≤ n ≤ m ≤ 250, 0 ≤ k ≤ n ) - the length of the string s , the length of the string t and the number of characters that Ivan can replace in his favorite string, respectively.
The second line of input should be a non-empty string s , consisting of n lowercase English letters - Ivan’s favorite string.
The third line of the input data is followed by a non-empty string t consisting of m lowercase English letters - text written in a newspaper. It is guaranteed that the length of string s does not exceed the length of string t .
Output
Output a single integer - the maximum number of occurrences of Ivan’s favorite string s after replacing no more than k characters in it in the text of the newspaper t .
Parsing
A naive solution that goes through all the options for changing the original string s and considers the answer for them has exponential complexity. However, we note that there are no more different variants having at least one occurrence than | t | - | s | + 1, that is, the number of ways to "attach" the string s to the string t .
We change the order of calculations, iterate all possible positions of the application of the string s to the string t, and for each we calculate exactly which positions and which characters need to be changed to get an entry in this position (or we can determine that it is impossible to keep within k changes). It is required in some way to code the necessary changes in order to be able to distinguish whether the line requires identical changes for two different positions of the application or different ones. In this problem there were small restrictions on the length of the strings t and s , therefore it was allowed to use almost any polynomial solution. For example, the necessary changes could simply be represented by an array of length | s |.
Now select the groups of the same changes and find the group of the same size. This can be done in many different ways, for example using sorting or hashes.
Problem C. Prize fund
Author of the idea and development: Alexey Dmitriev, MIPT
Subject: Math
Condition
HackerCook company has its grand championship in sports programming with a large prize fund, but the distribution of prize money has not yet been announced. The only thing that is known about the final distribution is that a participant with a higher place will receive no less prize money than a participant with a lower place.
Now, one HackerCook employee wants to distribute the prize fund so that his friends receive a sum of money as much as possible. Determine what part of the prize fund each participant will receive, provided that the employee distributes the money optimally.
Input data
The first line of the input data contains two integers n and k (1 ≤ k ≤ n ≤ 1 000 000) - the total number of participants and the number of friends of the Hacker Cook employee.
The second line contains k different integers a i (1 ≤ a i ≤ n ) in ascending order — the places that were occupied by the friends of the cunning developer.
Output
Print n non-negative integers b 1 , b 2 , ..., b n (
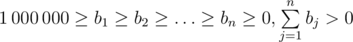), which means that the participant who took the i- th place must receive 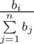part of the prize pool.If there are several possible answers, you can print any.
It is guaranteed that there is an optimal answer satisfying the condition described in the output format.
Parsing
Briefly: consider all the options to distribute all the money equally between the first few participants, at least one of these options will be the best answer.
How to prove it? Consider some optimal answer. Let there be some two participants A and B receive a different positive amount of money, let us denote their earnings by a and b (then 0 < a < b ). We divide all participants with a positive amount of money into those who received at least b , and those who received less b . Let in these groups X and Y participants, respectively, and among them x and y friends, respectively (at least one of the numbers x and y is positive).
Suppose we chose the number k and increase the earnings of each participant in the first group by k / X , and in the second group decrease by k / Y (note that the total amount is saved). Then the earnings of friends change to k (x / X - y / Y) . Note that we can pick up both positive and negative k in such a way that after a change no participant gets more money than those who are higher than him, and all earnings are non-negative. Since our answer is optimal, x / X = y / Y (otherwise, by choosing the number k of the desired sign, we could improve it). Choose k such that in the second group one of the participants has 0 money. The number of participants with a positive gain has decreased; we will repeat this process until all participants with a positive amount of gain do not equal.
Technically, the task is very simple: among all the prefixes of the sequence, you must choose such that the share of friends in it is maximum. This is done by a simple linear approach and saving the current answer as a fraction a / b .
Task D. Flowers
Author of the idea and development: Mikhail Mirzayanov, SSU
Topics: greed, event handling
Condition
Vasya wants to give Masha a bouquet on March 8. He knows one secret path in the woods outside the city, along which grow beautiful, and most importantly, free flowers. The path can be represented as a straight line, and we can assume that Vasya initially appears on it at point 0 and moves at a speed of 1, without taking the time to pick flowers.
Flower number i grows at the point of the path with the coordinate x i , and after Vasya breaks it, the flower remains alive t i units of time. Naturally, Vasya should dial an odd number of flowers into a bouquet, and they should all be alive at the moment when he brings them to point 0 to meet Masha (if the i -th flower is brought exactly t i units of time after it is torn off, then no longer considered alive).
Vasya is a straight line man, and even for the sake of Masha he is not ready to turn (that is, change the direction of his movement along the path) more than twice. Help him collect the largest bouquet of odd size.
Input data
The first line of the input data contains a single integer n (1 ≤ n ≤ 200 000) - the number of flowers growing along the path.
Each of the following n lines contains two integers x i and t i (–10 9 ≤ x i ≤ 10 9 , 0 ≤ t i ≤ 10 9 ) - the coordinate of the i -th flower and the time it will be alive after he'll be ripped off, respectively. At one point can grow more than one flower.
Output
Print a single number - the maximum possible number of flowers in a bouquet. If it is impossible to collect a bouquet from even one flower, output 0.
Parsing
The condition that Vasya is ready to change the direction of movement no more than twice clearly defines the form of the answer: first we go to one of the two sides until it stops, then, returning, we collect all the flowers, go through 0 and go the other way until some moment , then again we turn around and go to 0, again collecting all the flowers in its path. From how far we go from point 0 before the last turn, it depends, on the one hand, how many flowers we can collect on the way back, and on the other, how many flowers collected in the first section will have time to wither.
Without loss of generality, we will assume that we first went from point 0 to the left (negative coordinates), and then to the right. Then “turn the world” and solve a symmetric problem. Of course, we will collect a bouquet of the maximum size, and then we simply find the odd number nearest to this maximum.
A flower to the right of point 0 can be delivered to Masha if x i < t i for the corresponding i . Let us go to the right from point 0 to coordinate R. Then the flower i , located to the left of point 0, can be delivered to Masha uncomfortable if t i + x i - 2 R > 0 or R <( t i + x i ) / 2. Thus, n events are located along the ray with positive coordinates, each of which either adds a new flower or removes it. Go from 0 to the coordinates of the maximum event and find the maximum positive balance. It should carefully handle events located at one point and between integer points (here the problem will be solved by multiplying all coordinates by 2).
Problem E. Berland Hockey League
Author of the idea and development: Alexander Ostanin, MIPT
Topics: Mathematics, Graphs
Condition
In the championship of the Berland Hockey League n teams participate. The tournament is held in a round robin: each team plays exactly one match with each, and there are no draws in the tournament. Unlike traditional tournaments, the distribution of prizes in the Berland Hockey League does not depend on the final place of the team, but on the number of victories. Namely: all teams that have won at least w games receive prizes. Hockey expert Don Berry wonders if, based on the results of this tournament, exactly k teams will receive prizes. If such a tournament exists, you need to display a winner for each match.
Input data
The only input line contains three numbers n , w and k (2 ≤ n ≤ 1000, 0 ≤ w ≤ n , 0 ≤ k ≤ n ) - the number of participating teams, the minimum number of wins for receiving the prize and the number of winners of the tournament, predicted by the expert .
Output
If a tournament with such properties does not exist, output "NO" (without quotes) in the only line of the output.
Otherwise, in the first line print "YES" (without quotes). Then output n lines of length n , j -th character of the i- th of them should match the match between teams i and j . If i = j , then the corresponding symbol must be equal to 0. If the i team defeated the j command, then this symbol is 1, otherwise 0. For all i ≠ j, exactly one of the two symbols corresponding to the meeting of these teams must be equal to 1.
Parsing
We will solve a more difficult task: we will construct such a tournament, that the minimum of points among the first k teams is as large as possible, and the maximum points among the last n - k teams are as small as possible (it is stated that in some tournament the optimal values of these values are reached simultaneously). Then either this tournament is the answer, or there is no answer.
It is obvious that in the optimal tournament each of the first k teams must win each of the last n - k , it remains to decide how all the first teams will play each other and how all the last teams will play. We would like to see as many points as possible in the microtournament among the first k teams, and as many points as possible in the last teams tournament.
Let m teams participate in a tournament and m is odd. Then, in a complete graph on m vertices, all the degrees of the vertices are even, which means that there exists an Euler cycle in it (and it can be constructed in O (m 2 ) time ). If we orient the edges along the cycle and say that the edge leads from the winning team to the loser, we get a tournament in which each team won exactly (m-1) / 2 times.
Now suppose that m is even. Then it is impossible to build a tournament with the same number of points for all teams and the last team will have no more (m-2) / 2 points. But a tournament with such a property can be built if you throw out one vertex, apply the algorithm from the previous paragraph to the remaining m - 1 teams, and then put extra team wins in half of the remaining teams. In the resulting tournament, half the teams (m-2) / 2 points, and the other half - m / 2 points.
This way of building the most “even” tournament is suitable both for the first k teams and for the last n - k teams. In the end, we check that it really is the answer (that is, all the first teams won at least w times, and the rest won less than w times).
Problem F. Carlson
Authors of the idea and development: Gleb Evstropov, HSE, and Mikhail Mirzayanov, SSU
Topics: greed, dynamic programming
Condition
Twenty years have passed. Carlson is stout and no longer flies. The kid got a job, became a top manager and now lives in a huge house on the n- th floor.
Carlson decided to go on a visit to the Kid. Of course, he is not going to go up on foot, so on the first floor Carlson enters the elevator.
Buttons in the elevator are located from bottom to top in such a way that a person with an increase in h can reach any button corresponding to the floor from 1 to h inclusive. At the same time, on the i- th floor, Carlson has a friend with an increase in h i , and he can be asked to press any button he can reach. Of course, to ask a friend from the i- th floor to press a button, you first need to be on floor i . Carlson wants to get to the Kid, turning for help to the minimum possible number of friends.
Unfortunately, over time, Carlson's character also deteriorated, so sometimes he quarrels with his friends, but not more than one friend at a time. For each i, Carlson wants to determine the minimum number of friends to whom he will have to ask for help if he quarrels with his friend number i and cannot address him with a request to press a button.
Input data
The first line of the input data contains two integers n and h (2 ≤ n ≤ 10 6 , 1 ≤ h ≤ 10 9 ) - the number of the floor on which the Kid lives and the height of Carlson, respectively. The next line contains integers h 1 , h 2 , ..., h n - 1 (1 ≤ h i ≤ 10 9 ), the i -th of which corresponds to the height of a friend of Carlson living on the i- th floor.
Output
Output n - 1 number of ans 1 , ans 2 , ..., ans n - 1 , where ans i is equal to the minimum number of friends you have to ask for help if Carlson quarrels with a friend living on the i- th floor. If, having quarreled with his i -th friend, Carlson cannot get to the Kid, then output -1 instead of the corresponding value of ans i .
Parsing
First, we solve the problem under the condition that Carlson is friends with all his friends. At any given time, we can assume that some prefix of floors is available to it, because if Carlson could get to floor x , he could get to all intermediate floors. Then, obviously, the most profitable move will take the help of the highest friend on this prefix. The complexity of this solution is O (n) .
This immediately gives us a way to solve the original problem in a quadratic time — to sort through which friends Carlson is quarreling with and solve the problem for each case. Now we will notice that on each prefix we are interested only in two maximum values, and we will count the following values:
f i - the minimum number of steps for which Carlson can get to Tiny if he has access to the prefix of floors 1 to i and at the same time he did not quarrel with the highest friend on this prefix;
g i is the minimum number of steps for which Carlson can get to Toddler if he has access to the prefix of floors 1 to i and he has quarreled with the highest friend on this prefix (and therefore, he will have to ask for the second highest friend).
We denote by a i the highest friend among the first i , and by b i - the second highest. Then f i = f ai + 1, and g i = g bi + 1, if a i = a bi , and g i = f bi + 1 otherwise.
Now let's learn how to calculate the answer using these values. If one of Carlson's friends did not initially enter into the optimal answer, then the answer for the case of a quarrel with this friend is equal to the optimal one. If it did, then the answer for this i would be k - 1 + g i , where k is the sequence number of this friend in the optimal answer.
Problem G. Rock, paper, scissors
Author of the idea and development: Konstantin Semenov, MIPT
Condition
Petya and Vasya play the famous game “Rock, Scissors, Paper”. The game takes place in n rounds. In each round, Petya and Vasya choose one of three figures: stone, scissors, or paper. If the figures of the players do not match, the winner is determined in the standard way (the stone defeats the scissors, the scissors defeats the paper, the paper defeats the stone), otherwise a draw is declared. For victory, w points are awarded, for a draw - d points, for defeat - 0 points. The total score of each player is the sum of points for all rounds.
Petya determined in advance which figure he would choose in each round, and wrote it down as a string of length n with the letters r , s, and p . Here, the letter r at the i -th position in the line means that in the i- th round, Petya will choose a stone, s - scissors, and p - paper.
Vasya got a certain cyclical shift of Petr's line and wants to use this information to maximize his final score. Find the maximum score that Vasya can guarantee himself no matter what kind of cyclic shift of the source line is the line known to Vasya.
Input data
The first line of input contains three integers n , w and d (1 ≤ n ≤ 100 000, 0 ≤ d ≤ w ≤ 10 9 ) - the number of rounds, the number of points for the victory and the number of points for a draw, respectively.
The second line contains a string of length n , consisting of the characters r, s, p , the cyclic shift of the line written by Petya.
Output
Output one number - the maximum score that Vasya can guarantee himself.
Parsing
Suppose we have already seen the first few characters of Petina’s string and they make up the string t . Let f (t) denote the maximum bill that we can provide for ourselves; the answer to the original problem is f (empty string) . If the string length t is equal to n , the game is over and f (t) = 0.
Let t be less than n . If our next move is, for example, r (stone), in the worst case we will earn the minimum among the numbers: f (t + p) (the next Petin move is paper, we lost), d + f (t + r), w + f (t + s) . If any of these values is not defined (for example, if the string t + p is not a prefix of any cyclic shift), we set by definition f (t) = ∞. For the remaining two possible moves, the result in the worst case is calculated in the same way; since we can choose our next move, among the results for the three possible moves we choose the maximum, this maximum is equal to f (t) .
This method allows us to calculate the answer to the problem. All possible values of the string t , for which f (t) is not equal to infinity, are conveniently represented as a root tree, a boron, in which a letter is associated with each edge and a line is associated with any path from the root — a sequence of letters along which the path passes. The previous algorithm can be represented as dynamic programming on a tree in which all cyclic shifts of the source line are present. The tree size and complexity of the algorithm are O (n 2 ) .
To optimize, we need an advanced structure - a compressed suffix tree. We construct a boron, which contains all the suffixes of the string s , after which we “compress” into one edge a chain of vertices from which only one transition proceeds (now a line of some length is written on each edge). The resulting tree will contain O (| s |) vertices and edges; in addition, it can be constructed in linear time (for example, using the Ukkonen algorithm or using a suffix automaton).
Let's return to our task. If we calculate the value of f at the vertex, from which only one transition comes, we simply add w to the value of f for the only son of that vertex. This means that the method of calculating f is easily transferred to a “compressed” bur: when we go along an edge of length L, we add w ( L - 1) to the result.
Construct a compressed suffix tree for a doubled source line. This tree contains all the cyclic shifts of the original row, so it is possible to calculate the values of the function f from it , carefully examining cases where we go to the vertices at a depth greater than n . The final solution works in linear time.
If you are interested in such tasks, you can take part in the Russian Code Cup 2016 and compete for a cash prize!
Source: https://habr.com/ru/post/282241/
All Articles