Looking for a way - King Sultan masters the Laplacian

... He says: "If I live, I will visit, I will visit the wonderful island, at the time of Guidon."

In the kingdom of Saltan is not without a defect. A law has been passed - not to go beyond the cordon, but here Prince Guidon.

Again he sent a bow, but an invitation for a treat - a political decision must be made.



Palace intrigues, similar to toadstools, rose a wall - "they say, say that the patient." But I heard Sultan about the Guidons hookah, about the emerald squirrel, and the heroic arrow. And the main novelty is a young woman. In general, it was decided to go - "I have not been overseas for a long time."

')

There was, however, one problem - a route or scheme was needed. Since no one (except Wrangel Baron) knew how to get to the island of Guidon. The boatmen gave us a card, so I had to sit at the desk. Sultan leaned over the map, - where is the island of Buyan here? The task seemed familiar - to pave the way to Guidon’s Island. But how to find the road when there are too many ways?



Until the night, Sultan solved the problem, eventually he fell into hibernation. He dreamed of matrices and points, but in a swamp of hummocks. Neo jumped on a hummock from the island of Borneo.

- If you want to get to the deadline - swim by the maximum flow.

- What? - Saltan is almost awake. But Neo already turned into a hare.

Map and adjacency matrix

If you have not read "The Tale of Tsar Saltan about the potential of the Laplacian" , then you may be worth it now. We use the concepts outlined there.





Simplify the task of Saltan - consider only 7 islands. The map shows the possible paths between the islands and their length in days.





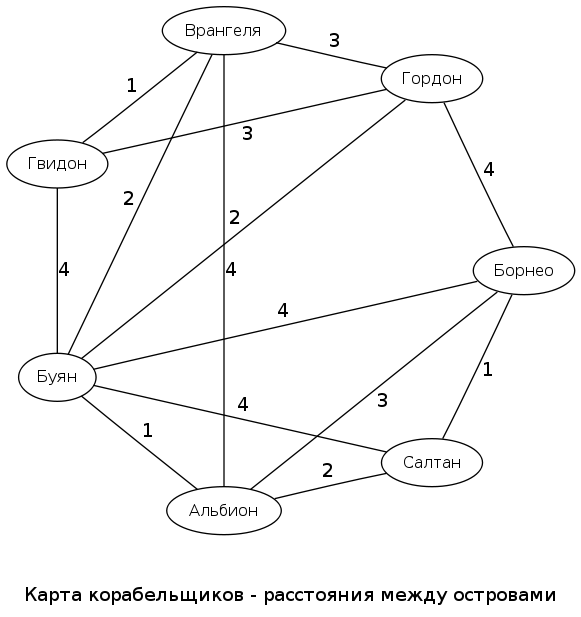
Yes, the map looks somewhat crooked, but let's not be too strict with the shipbuilders. Finding the best (shortest) path from Saltan to Guidon for this map is easy. Here it is: "(S) altan> (A) lbion> (B) uyan> (B) rangel> (G) widon". Total 6 days of travel.



We are interested in a common way to solve such problems - then we will be able to find ways for graphs of arbitrary sizes. There are various brute force algorithms , but this is not for us. We have the potential of the Laplacian and we want to use this potential.



The first step is obvious. It is necessary to go from the distance matrix to the adjacency matrix (connectivity). The greater the distance between the islands, the less they are connected. That is, the magnitude of the connection is inversely proportional to the distance. (In electronics it is similar - conductivity is inversely proportional to the length of the conductor).



Then the island adjacency matrix takes the following form (values ​​are rounded, 0.33 = 1/3):







This matrix (unlike those considered in the previous article) is symmetric, that is, the graph of connectivity is undirected.



The task of finding the path is divided into two. The first is to find at least some path between the given points, a method of guaranteed achievement of the goal from a given source. The second is to choose the optimal one from a variety of ways. In this article we will look at the first, relatively simple.



To solve this problem, we need a certain criterion that would allow to rank the islands depending on the distance to the target. Then, when choosing an island to which you can swim from a given point, we will know whether we are approaching the goal or not.

Island potentials

Such a criterion can serve as the values ​​of the potentials of each island. Yes, yes, the potential of the 1st order, which we used in the previous article. However, we cannot directly exploit the potential of the Laplacian. For symmetric matrices (undirected graphs), all values ​​of such a potential are equal to each other and are called the Kirchhoff constant matrix. In symmetric Laplacians, this constant plays the role of a determinant (determinant). We will further call the Kirchhoff constant a common (scalar) potential — simply a term (maybe not a particularly good one).



So, in symmetric Laplacians, the vector of potentials becomes a scalar - a common potential. For our Laplacian, the value of the total potential is approximately 8.61. It is considered simple - on the basis of the adjacency matrix, the Laplacian is constructed (as was described earlier), we delete any row and column from the Laplacian and consider the determinant. This is our common potential.



All this is great, but for finding the way is useless. What we need is that the potentials of the islands be different, and at the same time they change from maximum (Sultan) to minimum (Gvidon) or vice versa, without difference. How to achieve this?

There are two beautiful ways (and maybe more). The first one is classic. Therefore, we start with it.

1st method. Solve the Dirichlet problem

And the classic is to use the analogy of electric (well, Markov, too) circuits. Once we need different potentials, it means that we just have to apply the potential difference between the initial state (island) and the target state. This difference will lead to the fact that between the nodes (islands) will flow and, as a result, each island will have its potential.



It is important here that the values ​​of the potentials are harmonic , that is, the value of each potential is average relative to the values ​​of the neighboring potentials. Such harmonic vectors (functions) have one property - they take the minimum and maximum value on the border. In our case, the boundaries are the nodes in which the potential value is specified (fixed), that is, the islands of Saltan and Guidon. The harmony of the potential vector guarantees us that the potential will be maximal on one of these islands, and minimal on the other. And the potentials of the other islands will be somewhere between them. What we need.



If we assign a smaller potential to the island of Guidon, then when looking for a path from Saltan, we need to select only those islands whose potential is less than the current one and exclude islands with great potential.



It remains a bit - to find the values ​​of the potentials of the islands. This task is similar to the one we solved in the 1st article, so we will again present the balance equation in the form that emphasizes the harmony of the potentials U :







The difference is that now we have part of the potentials set. It is customary to call such values boundary . The term may not be very good, but generally accepted.



The problem of finding unknown potentials along known ones is usually called the Dirichlet problem. She has a solution (which pleases).

Fundamental matrix

Note that the magnitude of the connections (conductivity) between nodes, the potentials of which are given, do not matter. That is, they (these links) do not affect the decision. Therefore, the given (boundary) nodes can be excluded from the Laplacian. In our case, we exclude the islands of Saltan and Guidon from Laplacian. We get an extra laplacian minor, like this:







The inverse matrix of this minor is called fundamental (a term from the theory of Markov chains with traps). For our map, the fundamental matrix is ​​(check):







Next, we need the connection of external nodes (we have the islands of Saltan and Guidon) with internal ones. That is, the minor adjacency matrix, in which only two columns are left:







Multiplying the fundamental matrix by this minor communication of external and internal (worlds) we get the matrix of external influence on internal (and are close to completion of the maneuver). Here is our influence matrix:







The values ​​of the elements of this matrix reflect the contribution of external potential to internal. For example, the contribution of the potential of the island of Saltan to the potential of the island of Buyan is 0.513. Setting now the external potentials (Saltan and Guidon), we can calculate the potentials of all the other islands by simply multiplying the matrix of influence on the vector of external potentials. In my opinion, very cool.



The sum of the values ​​for each line is 1, that is, the weights of the contributions are normalized. This means that the closer the island is to Sultan, for example, the farther it is from Guidon, and vice versa.



In principle, this matrix is ​​sufficient for solving our problem of ranking islands, since, based on its values, we can already sort the islands by distance / proximity to the target. That is, we can reach the goal, but first consider

another way to calculate island potentials.

2nd Method. Perturbation of a symmetric Laplacian

Ranking island potentials across the fundamental matrix is ​​a universal approach. Like everything universal, it is a bit redundant (heavy) for our task. It is possible to do more simply, namely, to perturb the Kirchhoff matrix (the Laplacian of the islands).



As noted above, for a symmetric Laplacian, all components of the potential vector are equal. We need them to be unequal. Accordingly, it is necessary to make the Laplacian asymmetrical. How to do it is also understandable. Since we need a gradient of potentials from the island of Saltan to Guidon, then we need to resent the appropriate connection. This relationship will set the potential gradient.



What is “stir up the connection”? This means that in the adjacency matrix (conductivity) the value of the connection in one of the directions we increase by some delta (for example, by 1). In this case, the value in the opposite direction does not change. For example, we ask that the island of Guidon is connected with the island of Saltan, but there is no connection in the opposite direction.



In a sense, such a distortion (perturbation) of the adjacency matrix (and the Laplacian) is equivalent to the application of an external potential to the islands. After all, to maintain the difference in external potentials between the nodes, some kind of connection is needed (in electronics, a battery).



For a perturbed matrix, we can already calculate the island potentials as the first-order potentials introduced in the previous article.



Our perturbed mind of the Laplacian Islands looks like:







The difference from the unperturbed one is in the upper right corner, which is a “disturbance”. The vector of potentials of such a matrix is ​​equal (the method of calculation in the previous article):







The question arises whether the vector of potentials of the perturbed matrix and the vector of potentials calculated through the fundamental matrix are equivalent? In short, yes. It is easiest to verify this by substituting the perturbed potentials of the islands of Saltan and Gvidon (25.28, 8.61) as the given external potentials. Multiplying this vector of two values ​​by the influence matrix, we obtain the internal values ​​of the potentials.



Why did this happen? Let's try to figure it out. First, our perturbed potentials are also harmonic, since they satisfy the same balance equation. Secondly, the boundary values ​​of the disturbed potential are also always extreme — one of them (in our case, the Saltan potential) is maximum, and the other (Guidon potential) is minimal (if you change the direction of the disturbance, then the opposite will be the case). To understand why the perturbed potentials are extreme, we need to find out how they are considered / are obtained.

Derivative Capabilities

Suppose we need to rank the islands in a different order - not from Saltan to Guidon, but, for example, from Gordon to Albion. Each time, when changing the direction of the islands, the determinants and / or inverse matrices do not look like a good idea. Is it possible to count the opposite once, and then just use this opposite?



Let us see how the total (scalar) potential changes under perturbation. In the language of formulas, this means that we need to find the derivative (change) of the total potential when the value of a relationship changes. Luck is that, as mentioned earlier, any potential is determined by the sum of products of connections. That is, all conditionally linear and derivatives should be simple.



Dependence of the potential of the first order from the meaning of connectivity determined by the potentials of the 2nd order:







What is meant by “order of potential”? To obtain the potential of the 1st order, it is necessary to remove one lap and one column from the Laplacian. To obtain the potential of the 2nd order, it is necessary to remove two rows and two columns. For the 3rd, we delete three, and so on. For the matrix remaining after deleting the rows and columns (which is called the additional minor), we consider the determinant — its value will be the corresponding value of the nth order potential. Well, since we started to use the potentials of the 1st and 2nd orders, it is convenient to call the first the vector potential, and the second - the matrix potential.



In formula (2.1), the potential of the 2nd order is . The indices are separated by commas, the first ones are the rows to be deleted, the 2nd ones are the columns (possibly, on the contrary).



Let us assign indices to our perturbed islands. S is Sultan, G is Gvidon, and index B is on Buyan’s island. Then the change in the potential of the island of Buyan under the perturbation of the G – S bond can be expressed as







We calculate this change for our laplacian. Remove the corresponding rows and columns from the Laplacian and calculate the determinant. We get that . The same value is obtained if the potential of Guidon Island (which coincides with the total unperturbed potential) is subtracted from the potential of the Buyan Island: 17.15 - 8.61 = 8.55. That is, everything is correct, the formula works (this is because we have chosen a single perturbation - in the general case, we must not forget to multiply by changing the connectivity C ).



And what will happen if we calculate from the formula (2.1) the potential of perturbed islands - Saltan and Guidon? Substituting the corresponding indices into the formula (2.1 '), we obtain:







Translating into Russian, the potential of the island of Guidon under perturbation SG does not change (it remains equal to the total), and the potential of the island of Saltan changes by the magnitude of the main potential of the second order.

Types of potentials

Let's make a small digression to tell about the “main” and other types of potentials. We call potentials the main ones if the row indices removed from the Laplacian coincide with the indices of the columns. Therefore, for the main potentials, it is sufficient to specify only one set of indices, i.e. .



And what non-main types are? Two more situations are possible - the deleted set of row indices intersects with the column indices (let's call such potentials adjacent) and does not intersect (free potentials). In the formula (2.1) involved the adjacent potential (the intersection of the index k ).



Now, attention! The gift of the gods is that all non-main potentials can be expressed in terms of the main ones. Here is a general formula for symmetric Laplacians:







from which the expression for adjacent potentials follows:







Substituting (2.4) into (2.1), we obtain the connection of the derivative of the potentials of the nodes with the main potentials:







That ladies! This formula is the tool we were looking for. It remains to inspect, start and you can use.

2nd order potential matrix

So, the truly fundamental matrix for symmetric Laplacians (undirected graphs) is the second order prime potential matrix. We give her view for our islands:







Calculate on this matrix the increment of the potential of the island of Buyan with the perturbation of the connection between Saltan and Guidon:







We have seen this figure before, so it looks like the formula works.



How to get this matrix for a given Laplacian? You can, of course, stupidly delete rows / columns and consider the determinants of the minors, but this is costly and inefficient. Therefore, it is usually done differently. Take the additional minor of the laplacian (that is, remove any, for example, 1st, row and column) and calculate for it the adjoint matrix (the adjoint is the inverse, the values ​​of which are multiplied by the determinant). The matrix obtained in this way is a collapsed potential , but it can be expanded by applying distance conversion to the values ​​(yes, a lot of obscure terms, but somehow you need to call it all). As a result, we obtain the desired matrix potentials. That is, here is Horner’s scheme:



Potential matrix = Distance (Attached matrix (Aux. Minor (Laplacian)))



The distance conversion is as follows:







for symmetric matrices







The matrix of potentials is directly related to the matrix of resistive distances (the values ​​differ by a factor of the total potential), as well as to the Green matrix, which is the inverse of the Laplacian , but about all this some other time.

Geometry Relationship

The values ​​of the matrix potential are proportional to the squares of the distances between the nodes of the graph. In fact, if we take a closer look at the values ​​of the matrix and compare them with the shipbuilders card, we will see that this statement seems to be true - the largest value (16.67) between the islands of Sultan and Gvidon.



This suggests that the derivative of the vector potential can be given a geometric meaning. We write the formula (2.5) in the form







(here we used the notation ), and compare this formula with the cosine theorem known from the school course







Then we obtain the following relationship between the derivative of the vector potential and the parameters of the triangle (the indices lead to the notation for the vertices of the triangle i = C, j = B, k = A ):











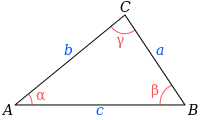
Formula (2.7) describes the change in the potential of the vertex C with a change in the conductivity (connectivity) of the opposite side of the triangle - BA . Note that the formula is asymmetric with respect to the permutation BA . This is due to the fact that the derivative of the potential depends on the direction:







If you change the direction, then the value of the derivative will be expressed through other sides and a different angle:







Formula (2.7) demonstrates the extremality of the potentials of the perturbed side of the triangle. Since the values ​​of the cosine of the angle are always (in absolute value) less than 1, it is obvious that the extreme values ​​of the potentials of the triangle will be only if the vertex C coincides with one of the other vertices of the triangle ( A or B ). Such is the unexpected connection between the properties of harmonic functions and the properties of a triangle.

Summary

It's time to wrap up. Take a look back. We looked for a way to define paths between nodes of an undirected graph, and we started with a method of ranking nodes. This is a general method that is applicable not only for path finding tasks.



Suppose we have a set of symmetrically interconnected objects (a connection can reflect, for example, the degree of proximity of objects). We can not sort the data objects if we do not have a sorting criterion - all objects are the same. But if we now choose some two objects from the set and indicate that one of them is the largest and the other is the smallest, then all other objects can be ranked according to their degree of closeness to large or small. By simply specifying the boundaries (large and small objects) we polarize the rest of the objects (give them different potentials) with respect to the given boundaries.





It is interesting.

Well, yes, it is too early to sail. We found a way to guarantee a destination, but did not indicate how to find the optimal (shortest) way. Continued here.