Floors: 3D-navigation on WebGL in 2gis.ru

In 2014, 2GIS released Floors - this is a feature that allows you to see the floor plan of the building and find the necessary organization on it. For a long time, it existed only in 2GIS mobile applications. Now this feature has appeared in the online version .

The floors for the web are made on the WebGL technology: they are completely three-dimensional, they can be twisted and brought closer. This is the first project of the company, made on this technology, and we would like to share the experience of implementation.

Technology stack

The WebGL technology, which allows you to do full three-dimensional graphics with hardware acceleration in the browser, is quickly gaining popularity in web mapping. As successful examples of its use, you can cite the already mentioned Google Maps here, as well as the Mapbox GL library.
')
The advantage of maps made on WebGL, in smoother transitions and animations, as well as the ability to flexibly control the appearance of the map. For example, Google maps can draw shadows from houses on the ground, the shape and size of which correspond to the current time of day. Obviously, in traditional web maps that work on tiles, this is impossible: you can never change the once-updated tiles, you can only show them as they are.

The disadvantage of WebGL is the high complexity and high threshold of entry. Therefore, despite the fact that the technology is already 5 years old, its popularity is still low. We have long wanted to try out WebGL on some not the most difficult task, and the Floors became an excellent opportunity to do this.

Our project consists of a WebGL application embedded in the 2GIS online version and a backend that distributes data to it. When entering the Floors, the application loads data from the backend and draws a building from it.


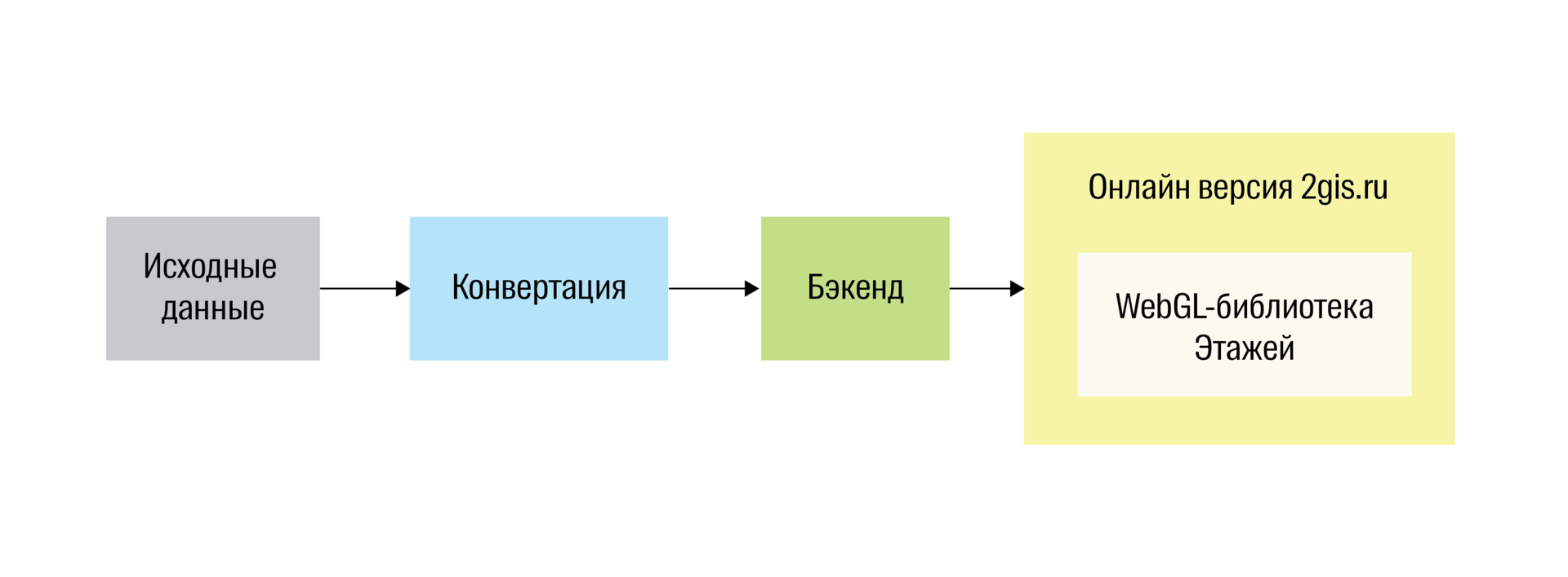
Architecture of Floors

In their original form, the data represent a set of ordinary WKT geometries — area-rooms, lines-walls, and points-POI. In this form, they are not suitable for rendering in WebGL, so you must first prepare them: we remove all unnecessary from them, add volume to flat geometries, and triangulate everything. All these operations are performed on the server. To do this, we have written a separate conversion application.

Working directly with WebGL is difficult: it’s a low-level API where you have to write a lot of code to achieve the simplest things. Our introductory article on WebGL describes how to draw a rotating cube on a pure WebGL, and the full code of the resulting example takes up more than 200 lines. Therefore, at an early stage of development, we used the popular three.js WebGL framework.

However, three.js is a heavyweight combine with a huge number of possibilities, of which we used only a small part. Therefore, at a certain moment, we replaced it with our own 2gl library, which contains only what we need.

The use of its library has reduced the size of the application’s assembly more than twofold and significantly improved its performance.

How we overcome difficulties

Developing a WebGL engine for drawing floor plans is far from the most standard task for a front-end developer. During the work on the Floors we had to solve many unusual, interesting and often unexpected problems, some of which we decided to write in this article.

How to make a flat volumetric?

When we started working on the floors and began to study the format of the source data, it turned out that they are not even three-dimensional. The shape of each floor is represented by a set of two-dimensional areal (room) and linear (wall) geometries. For flat display of floors in the mobile version 2GIS of this format is enough. We also had to figure out how to give the floor volume.

There were no problems with the squares: we just draw them on the floor. But with the walls had to tinker. At first we tried to just take the lines and make of them flat walls of zero thickness. It turned out ugly:


Early prototype Floors with flat walls

In the real world, walls are thick. The same thing had to be done in the Floors.

So, you need a set of broken lines to get a set of three-dimensional wall geometries. In general, the solution to this problem is nontrivial. But we decided to go from simple and first tried to implement the simplest and most obvious solution "head on."

1. Find all the intersection points of the walls.
2. For each intersection point, we iterate through all the pairs of walls that form the corners.
3. For each such pair we measure the angle between them.
4. We draw the bisector of this angle and put the “corner point” on it - it will become the outer border of the future thickened wall.
5. Connect all the corner points and get the outer contours of the walls.

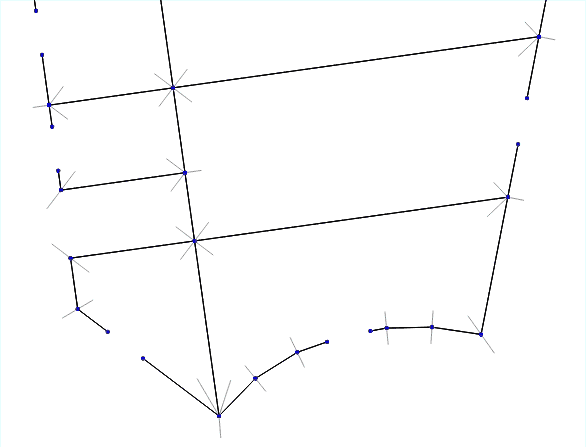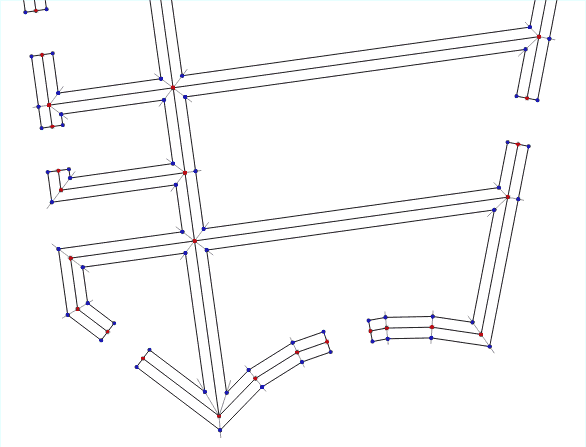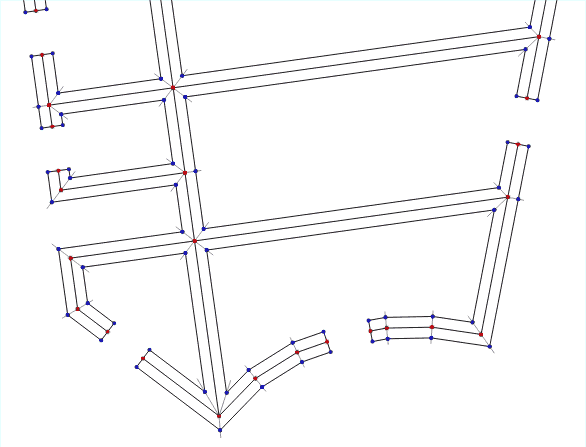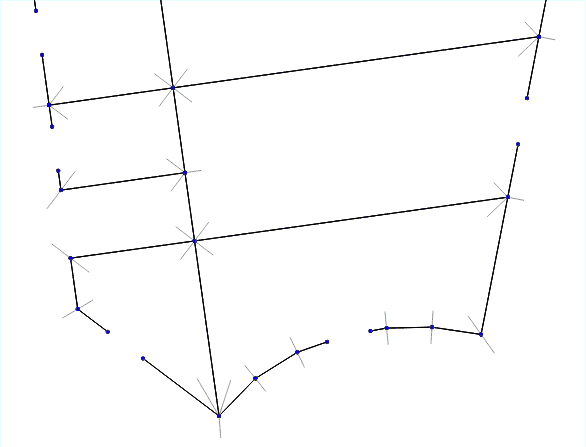
Animation of the algorithm for different wall thicknesses

This simple algorithm works well only if a small wall thickness is required. If the walls need to be moved apart far, and especially if there is an intersection at acute angles in the data, the result will already be incorrect:


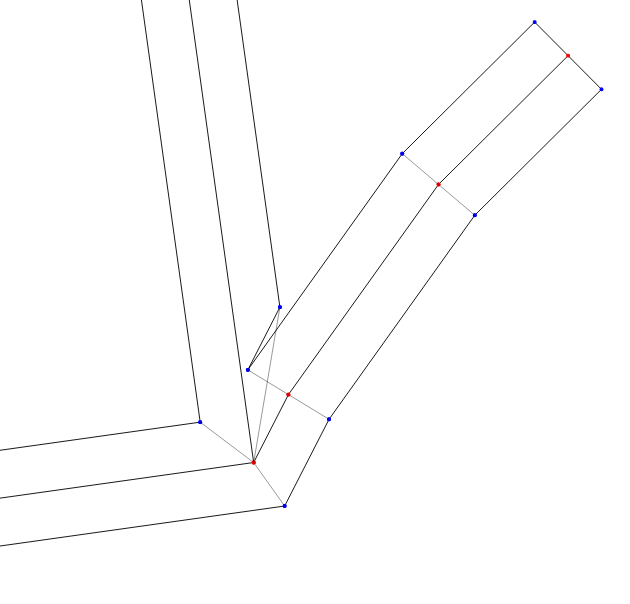
With a large thickness appear artifacts

However, when we looked at the results of his work, it turned out that on our data he gives good results in 100% of cases, so it turned out that it was not necessary to invent something more complicated.

As a result, we got beautiful, voluminous walls in the floors, solving the potentially complex task of hundreds of lines of simple code:


The walls are now material

How to program inertia?

No modern cartographic engine can do without inertial movement while dragging a map. Due to inertia, the map behaves like a material object, it becomes intuitively simple and pleasant to move it. Inertia is one of the first things that a user sees and feels when he opened a card a second ago and started moving it. Therefore, it makes a particularly large contribution to the overall impression of using the card.

How inertia in general is arranged in maps can be found in this article . The solution described in it has one drawback: in it, the slowdown animation relies on the periodic challenge of a special function, which in each frame reduces the speed of the map a certain number of times. Such an implementation will work correctly only with constant FPS. If the FPS goes down, this function will be called less often, and the animation will last longer than necessary.

To remove the dependence on FPS, it is necessary to calculate the position of the map based on the time elapsed from the beginning of the animation. It is necessary to calculate it by some formula.

What should this formula be? The first answer that occurred to us was the kinematic equation of uniformly accelerated motion from the textbook of physics for the eighth grade. Here it is:



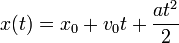
Here:
x0 - starting position
v0 - initial speed
a - acceleration

Perfect! x0 and v0 are known to us, and by selecting the value of the constant a, we can adjust the animation. And most importantly, the inertia, working on such a formula, will be realistic and make a good impression.

So we thought, until we programmed this formula. It turned out that she works very badly. With small values ​​of acceleration, the shopping center went out of control of the screen uncontrollably after the slightest mouse movement, like a car on slippery ice, with large ones - the map stopped almost instantly after a dredge.

Both versions created an equally unpleasant impression: in the first case, the sense of control was lost, in the second, the impression was of a poorly oiled mechanism. There was no way to find a middle ground.

Tired of trying in vain to find the optimal acceleration, we tried to use instead of the physical equation one of the Robert Penner easing functions , which have been used for js animations for many years and are built into many libraries.

The result was great: after the dredge, the map stopped smoothly and gracefully, without leaving too far. And despite the fact that its movement has ceased to be “correct” from the point of view of physics, it has become much better perceived.

We experimented with different easing-functions and eventually wrote our own, which worked exactly as we wanted, but this is not the most important part of the story. The most important thing is a simple lesson that we learned: realistic animation does not mean good animation.

How to sign the rooms?

We designate rooms and objects on the floors with the help of markers and signatures to them. How to draw markers in a WebGL application? The simplest solution is to create a DOM element for each of them and display them on top of the WebGL canvas. On each frame, it is necessary to calculate the new position of each marker and move the corresponding DOM nodes.

We had to almost immediately abandon this idea for one simple reason: DOM is too slow. The need to update the position of a large number of DOM elements for each frame led to an increase in the frame rendering time tenfold.

Only one way out - to use WebGL sprites. It is enough to draw a rectangle (namely, two triangles), drag the desired texture onto it and place it in the 3D scene. This is how, for example, monsters were drawn in old 3D shooters:


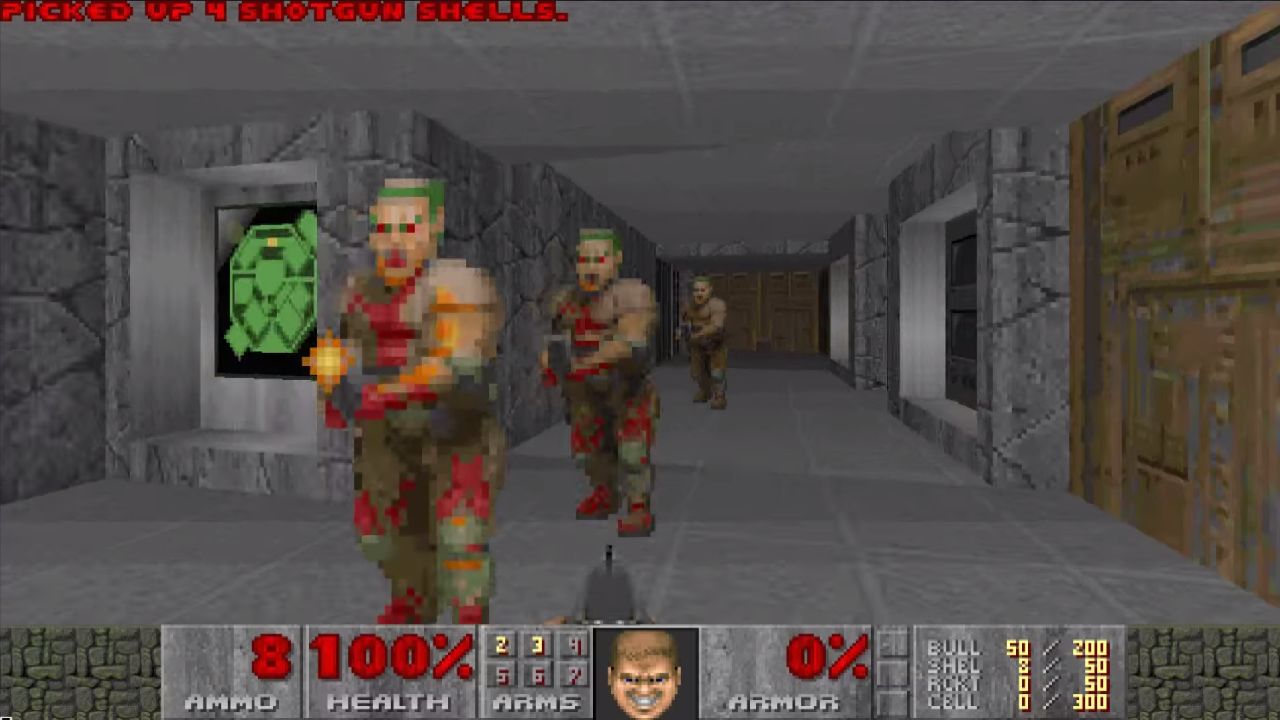
Almost what we need

The markers in the floors differ from the zombies in Doom II in only one detail: their size does not depend on the distance to the camera. This requirement is easily implemented using a custom vertex shader: we wrote a special shader for markers, which positions the vertices of the sprite exactly as needed to maintain a constant size in pixels.

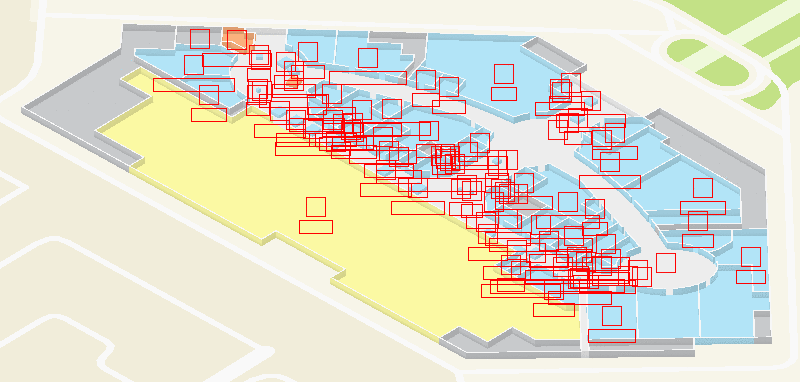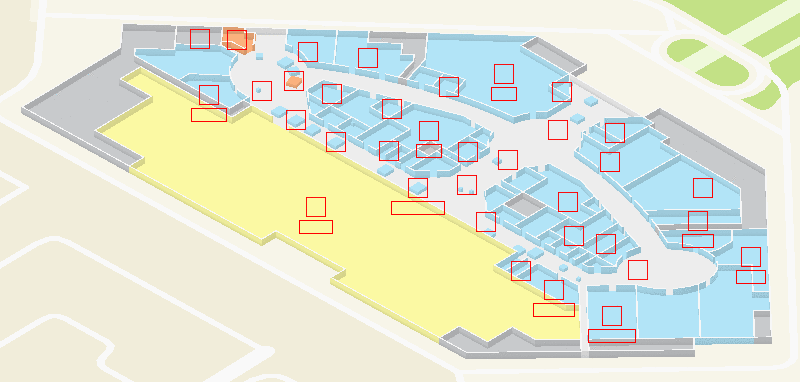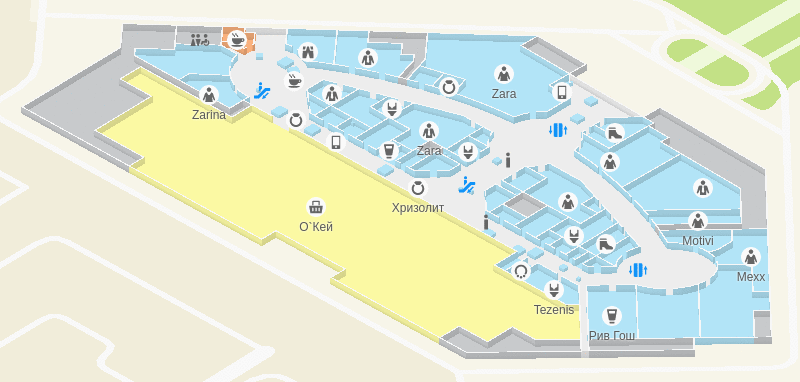
Drawing WebGL sprites is very fast: you can map thousands of objects without losing performance. But when there are too many markers on the map, the following problem appears: they overlap.


What happens if all the floor objects are signed simultaneously?

A common solution to this problem is marker clustering . This approach consists in the fact that among the set of all markers, the groups of the closest ones (clusters) are distinguished, and when the scale is reduced, the cluster is replaced with one collective marker.

In the floors we use a simpler approach, which we called generalization: we simply assign each marker some priority and hide the low priority markers if they overlap the more important markers.

To check the intersection of the markers, you need to represent them in the form of bounds - rectangular areas that they occupy on the screen. We choose priorities based on the type of marker: for example, infrastructure facilities (elevators, toilets, etc.) have the highest priority, so they will always be visible even on the smallest scales.


The work of generalization: leave the most important

A naive implementation of such an algorithm has a quadratic complexity: each marker must be checked for intersection with all the others. To make it work faster, we used the excellent rbush library, which implements the R-tree data structure. An R-tree can store rectangular areas and quickly search for their intersections - this is exactly what we need.

After applying rbush, the complexity becomes n * log (n), and on the floors of the Dubai Mall (up to 1000 objects per floor) the algorithm works in ~ 10 ms. By moving its execution to a web worker, we completely excluded its impact on the FPS.

The last difficulty in drawing markers on WebGL is to make them clickable. DOM elements have events (click, mouseover, etc.) that you simply subscribe to; there is no such thing in the world of WebGL. Therefore, it is necessary to learn from the coordinates of the cursor to determine which marker the user clicked.

Here, the rbush library comes to the rescue again: it is enough to build an R-tree containing the bounds of all currently visible markers, and to process the click, simply search for it. An R-tree search is a logarithmic operation, it is performed quickly, and you can easily perform it not only by a click, but also by any change in the position of the cursor. This allows markers to be sensitive not only to the click, but also to mouse over.

How to make isometry beautiful?

It is easy to see that an isometric view is used in the floors, which is quite unusual for web maps.

If a conventional perspective projection is better suited for ordinary three-dimensional maps, the layout of the room looks much better in isometric. In this projection, distant objects have the same size as the close ones, due to which the map becomes more visual and nicely schematic. Moreover, it is just beautiful.

An isometric projection has one drawback: it looks unevenly at different angles of rotation of the map. If you rotate the camera so that the walls are arranged vertically and horizontally on the screen, you get the following picture:


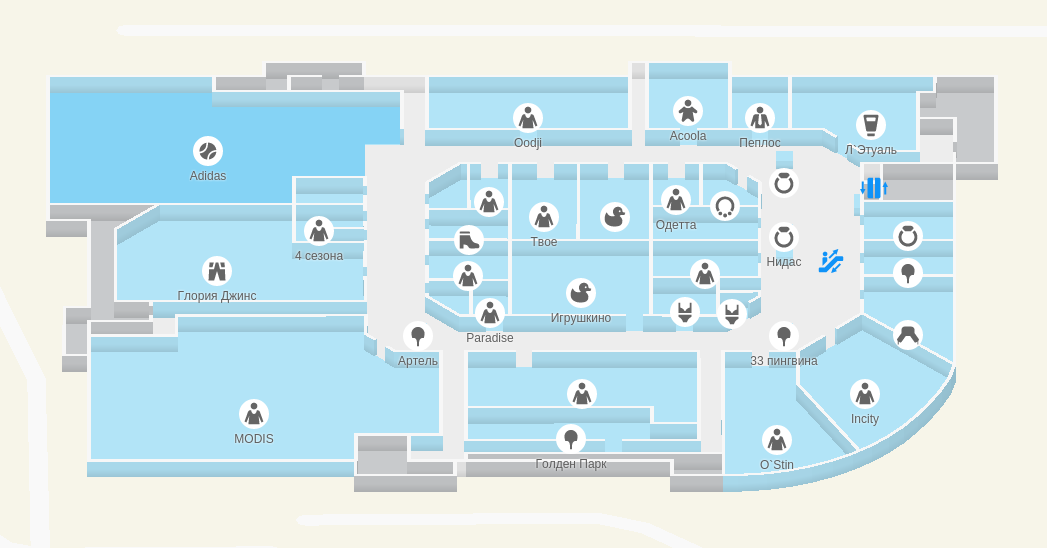
Unsuccessful steering angle

This is not very beautiful: the vertical walls are almost invisible, the map does not read well.

Initially, we opened all the buildings in the default position “north to the top”, and the shopping centers, where the walls are located along the parallels and meridians, looked exactly like that.

If the camera is slightly rotated and the walls are arranged exactly as it should be in isometric, it turns out like this:


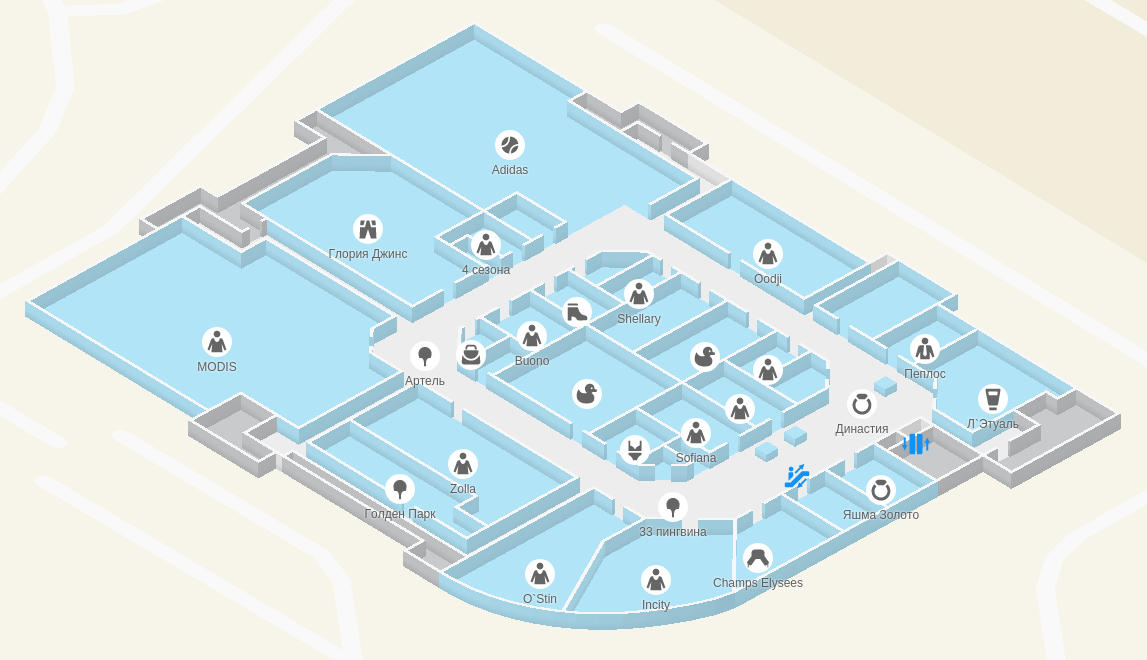
Good angle of rotation

Much better. This kind of familiar to us for a large number of old-school (and not very) games that use isometric:




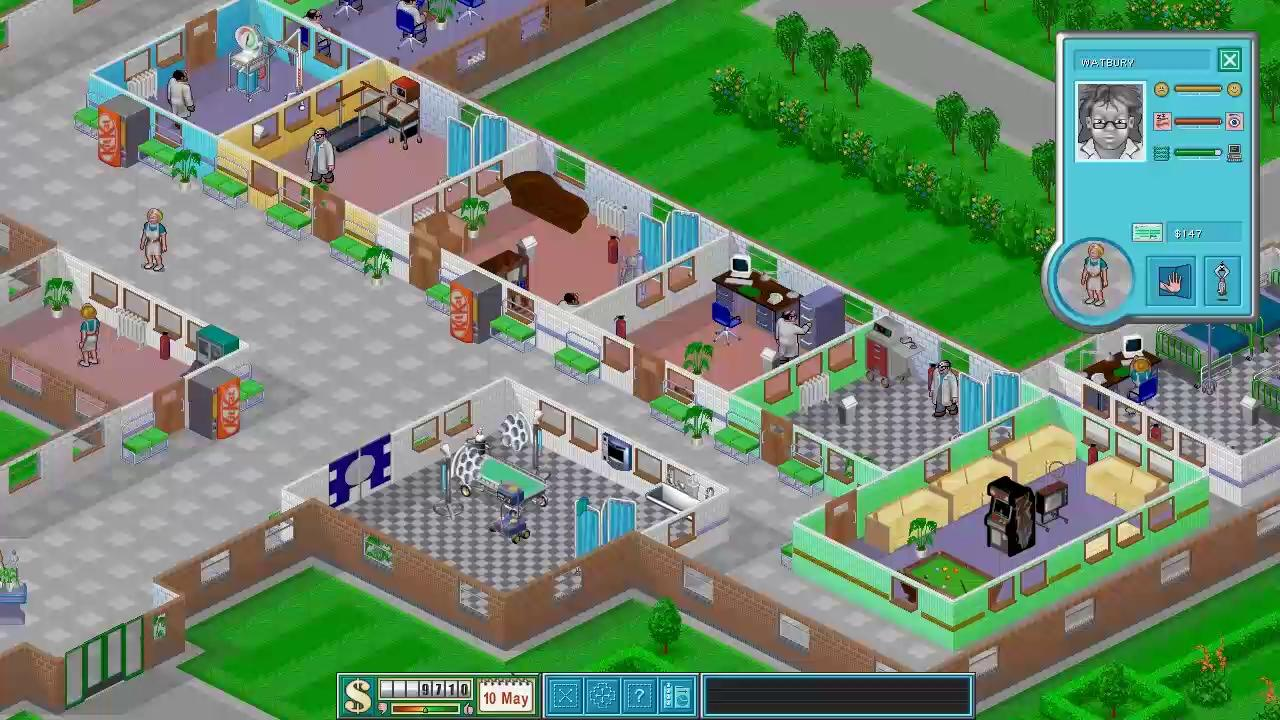
Fallout 2 and Theme Hospital

Thus, we faced the task for each shopping center to calculate the most optimal angle of rotation, so that when opening the floor mode, to present it in the best possible way.

If the architecture of rooms in isometric games is usually simple (all walls are perpendicular), then with real buildings everything is not so simple: in our data there are shopping centers of very odd forms, where the walls intersect at the strangest angles.

However, we noticed that even in the most complex buildings, there is some direction in which the overwhelming majority of walls are located.

This fact we decided to use. In mathematics, this prevailing frequency is called “fashion.” When preparing data, we tried to measure the angles of each wall of the shopping center and find the fashion of the resulting set. Adding to the PI / 4 mode found, we obtained the desired camera angle.

The algorithm showed excellent results: it accurately determines the “main direction” of the walls and unfolds a building on them.


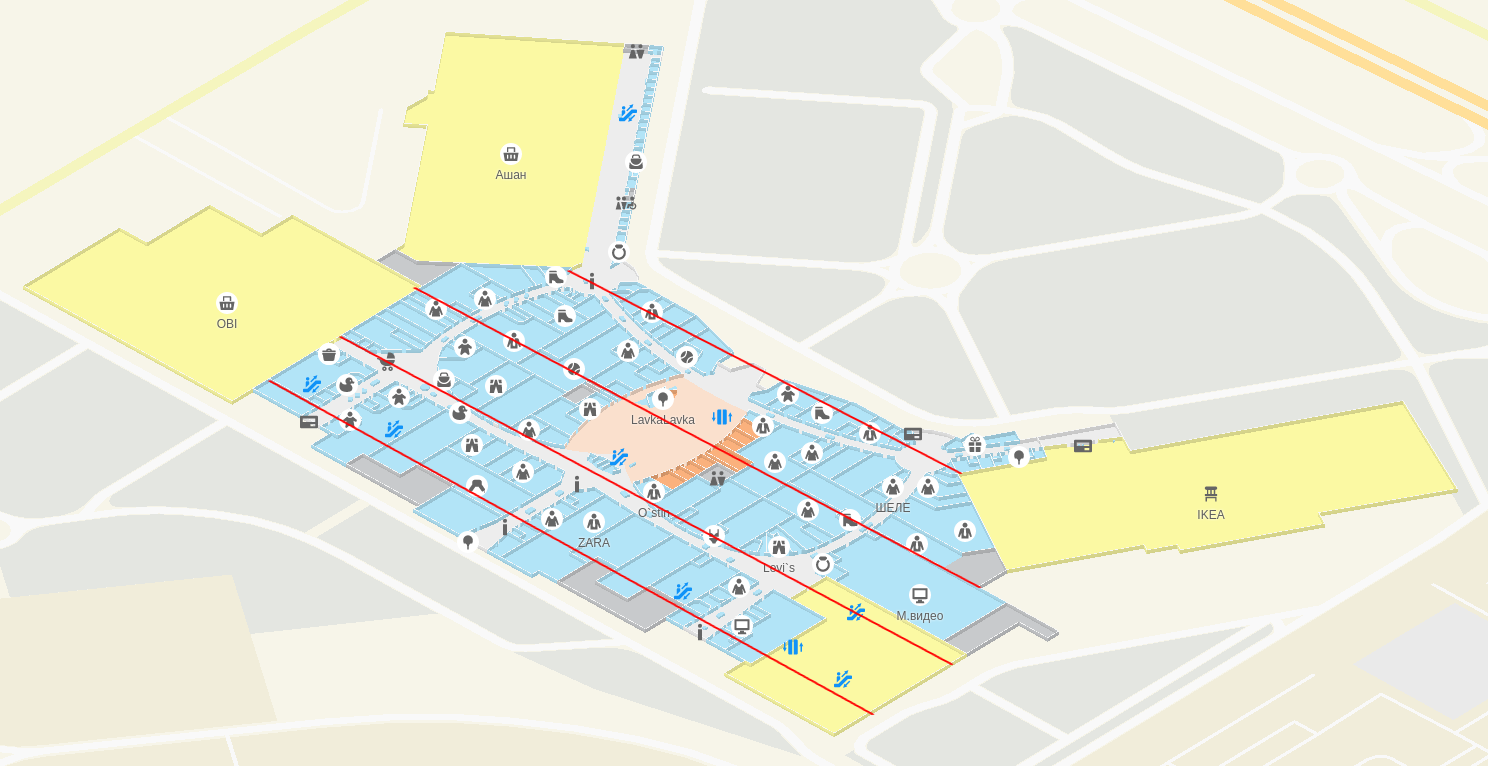
Properly deployed shopping center "Mega Khimki"

In mathematics, if the set contains more than one mode, it is called multimodal. Opening different buildings on the Floors at 2GIS, one can see that this term can also be applied to some shopping centers:


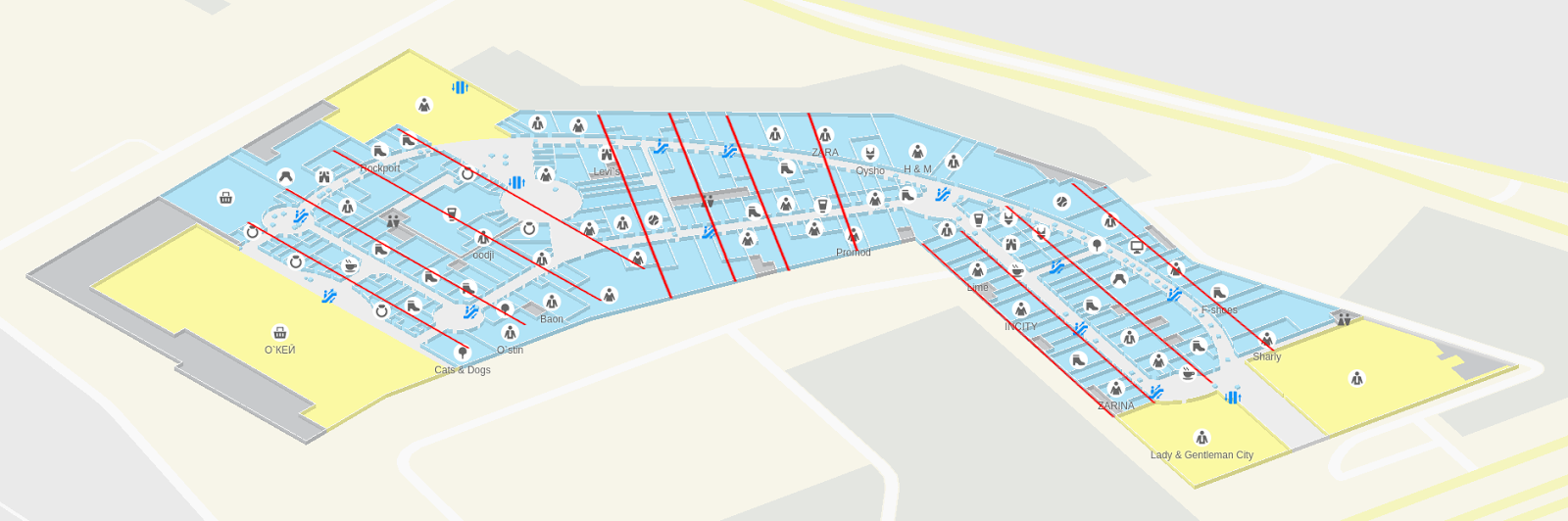
TC "Golden Babylon" with three mods

Despite the fact that the mod is several, one of them is more fashionable. According to it, we develop a plan for a shopping center. Mathematics is sometimes manifested in our lives in the most unexpected forms, and this is perhaps one of these cases.

findings

Most of the time the Floors were developed by two programmers. When we started working on the project, none of us knew anything about WebGL, or about 3D graphics in general, and we had quite a modest experience in web development.

The first versions of the Floors looked scary and worked at best at 20FPS. During the development, we stuffed all the bumps that could stuff, more than once rewrote large parts of the project. But the result each time was slightly better than the previous one, and it inspired us from the very first prototype, and it still inspires.

Do not be afraid to try WebGL: this technology allows you to do really fantastic things .