Liscript - we realize TCO

In my last article, Writing a Lisp Interpreter in Java, I briefly and abstractly told about what I wrote a couple of Lisp-like interpreters that I called Liscript - in Haskell and in Java. There is nothing particularly unique and outstanding in this, but for me it was a pleasant, interesting and informative pastime. Among other features, I mentioned the implementation of TCO (tail call optimization) - the optimization of the tail function calls by the interpreter. This question aroused the interest of individual community members, and a proposal was made to disclose it in more detail in a separate article, which I tried to do. I ask those interested under the cat.

At first, I still allow myself to briefly outline some of the basics, because I will further refer to them to complete the picture.

Eval without Apple - like Miklouho without Maclay

The simplest interpreter of expressions in languages ​​of a Lisp family can be implemented as a pair of functions (pseudocode):
')

eval (expr, env) // expr - , env -  if typeof(expr) = Atom //   -  return lookup(expr, env) //       elseif typeof(expr) = List //   -  evalexpr = mapeval(expr, env) //     //   eval //     return apply(evalexpr, env) //    else return expr //    apply (expr, env) // expr - , env -  op = head(expr) //  -    args = tail(expr) //  -   case op of .................. //    .................. //      .................. //    .................. //      ... //     Function f: //   -  newenv = subenv(args, f.clojure) //   -   return eval(f.body, newenv) //    //     

In the code above, much is simplified, for example, we don’t need and even misinterpret the entire list if the type of its operation is a conditional expression, but these are details. It was possible and not to allocate the apply to a separate function by implementing the case on operations directly in the body of eval, it does not matter. It is interesting that in these functions there are no cycles and destructive assignment and change of variable values, therefore in this form the interpreter can be used in any programming language that supports function calls, recursion and has (or has the ability to create) several data types, such as a simply-connected list, tree of dictionaries for the environment, and types of works (structures / classes with fields). Also, if we leave aside user interaction (I / O) in the computation process, then these functions are “pure” in terms of functional programming. But even if it is possible to make internal I / O in the middle of a computation, then this variant of the interpreter is directly implemented even in a pure functional language, for example Haskell, or in any imperative language with sufficient minimum capabilities. But in the latter case there may be a limitation - the calculation function actively uses recursion, and with a small stack depth it will overflow. The situation is all the more aggravated if the implementation language does not support tailing call optimization - TCO.

Problem

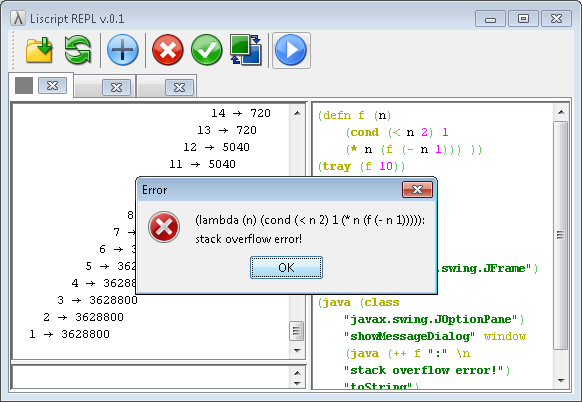
I faced the problem of stack overflow when I implemented the interpreter in the Java language. Each calculation was launched in my separate thread, and by default the stack size for one thread is very small. I saw the following solutions:

• increase in the size of the thread stack, is set via a special key when the program starts. Does not solve the problem completely - the maximum stack size is also limited, but does not require any costs.
• implementation of a different interpreter structure, for example, on a register machine (see SICP). I have not tried it, but I think it will solve the problem of tail recursion only.
• sequential computation in multiple threads. When implementing, I encountered the difficulty of writing a reliably working version.
• transfer calculations from stack to pile - springboards, etc. The naive implementation of the iterative conversion of the entire AST was very slow, but did not master the optimal one.

Most likely there are good and reliable solutions to this problem, but ultimately I settled on a compromise - implemented in the above simple version of the TCO interpreter, and together with the possibility of increasing the size of the flow stack, this allows in many cases to avoid overflow. This interpreter was conceived as a toy, pet project, so this compromise solution suits me so far. But I do not exclude the possibility that in the future I will come up with a better solution.

Decision

The key to the solution is, when it is possible, not to call the eval function again and again recursively, plunging deeper into the stack, but to organize an explicit loop inside it in which to perform the necessary calculations. To do this, you can proceed as follows - divide the calculation of the result of applying the function to the arguments into 2 options - let's call them conditionally “strict” and “lazy”. With a strict calculation, the function will still return the final result of the calculations, and with a lazy one, some intermediate object that will contain the function itself (along with its body and its own environment, which is part of its attributes), and a list of the calculated values ​​of the arguments with whom she should be called. Let's call this object FuncCall, below is the code of the function classes and FuncCall (the latter does not contain JavaDocs because it is an internal private class, but its essence is trivial and understandable without explanation):

  /**   Liscript -  */ public static class Func { /**      */ public ConsList pars; /**   */ public Object body; /** ,     */ public Env clojure; /**  * @param p      * @param b   * @param c ,     */ Func(ConsList p, Object b, Env c) { pars = p; body = b; clojure = c; } /** @return    */ @Override public String toString() { return showVal(this); } } private static class FuncCall { public Func f; public HashMap<String, Object> args; FuncCall(Func _f, HashMap<String, Object> _a) { f = _f; args = _a; } @Override public String toString() { return "FUNCALL: " + args.toString(); } } 

To complete the picture under the spoiler, the Env class code implements a hierarchical environment with the methods:


The logic of the work was the following: in the code text, the programmer explicitly marks (in my case with the help of an additional special form) tail function calls. When calculating such calls, the lazy FuncCall is returned, and right there in the cycle it is calculated, while the return type is all the same FuncCall, and as soon as we get a different type in the calculation, we return it as a result. In my implementation, new objects are created in the loop each time, but the garbage collector built into Java takes care of them. But we implemented an iterative imperative loop inside the recursive function of computing, and our stack stopped growing with tail calls. Everything worked, the only inconvenience was that the text of the code required to explicitly specify tail calls. Without this, calculations were performed as usual, with a dip in the stack. I wanted the interpreter to determine the tail calls itself, and calculate them in a loop. This was implemented through the optional parameter of the eval function - the strict boolean flag of strict / lazy evaluation of functions. The logic of operation is the following: for any value of the flag, when calculating a function, first a FuncCall object is created with this function and calculated values ​​of the arguments. But with strict calculation, this object is immediately calculated in a loop, but with a lazy calculation, while the type of the result is FuncCall. With a lazy calculation, the created FuncCall is immediately returned as a result. Nowhere else does the value of this flag determine the logic of operation, but it was necessary to choose in which nested calls it should be calculated strictly and in which with the flag value transmitted in the input parameter (to preserve the severity / laziness of the external calculation). But it turned out to be not difficult - when choosing always a strict calculation, in addition to calculating the last element of the list, the result of the conditional expression (the conditions themselves are strictly calculated) and the runtime macros - these 3 cases are calculated with the incoming flag value, in all examples the interpreter correctly determined tail calls, and optimized them, including cross-recursions. In the code, it looks much more concise than a verbal description:

  else if (op instanceof Func) { Func f = (Func)op; //       FuncCall FuncCall fcall = new FuncCall(f, getMapArgsVals(d, io, env, f.pars, ls, true)); if (strict) { v = fcall; while (v instanceof FuncCall) { FuncCall fc = (FuncCall) v; v = eval(d, false, io, new Env(fc.args, fc.f.clojure), fc.f.body); } return v; } else return fcall; 

An example of work in the interpreter (the functions foldl and foldr are defined in the standard library, here their definitions are duplicated for clarity):

 def a (list-from-to 1 100) => OK def b (list-from-to 1 100000) => OK defn foldl (fal) (cond (null? l) a (foldl f (f (car l) a) (cdr l)) ) => OK defn foldr (fal) (cond (null? l) a (f (car l) (foldr fa (cdr l))) ) => OK foldl + 0 a => 5050 foldr + 0 a => 5050 foldl + 0.0 b => 5.00005E9 foldr + 0.0 b => java.lang.StackOverflowError 

Among the special forms of the language is the tray service command, which prints a call stack with an indication of the calculation step and the recursive call nesting level, then you can see "in a section" which calls are received with different options:





The source code of the interpreter is still available in my repository on Github .