Mathematical model of perception (Part 1)
Part 2
Part 3
The purpose of this work is to show how languages like English, as a natural and effective method, can arise at different levels of the process of perception. Along the way, the issues of mechanisms that allow us and animals to see, classify color spots by shape, get an idea of places, objects and their geometric properties are touched upon. A few words are devoted to purely linguistic problems: which concepts and methods should be present in any sufficiently expressive descriptive language among the initial ones, and which, as derivatives, can be derived from the initial ones.
How could language participate, for example, in the process of visual perception? Each of us is used to talking about our ability to see a tree, to hear the birds singing and to feel warmly, holding our hand over a candle. Yet our To consciousness, neither sound, nor heat, nor the sensation of light is directly accessible to perception. The idea of all this is formed solely on the basis of the properties and patterns of irritation of our recipes. To understand the complexity of the tasks arising in such cases before the brain, imagine that, instead of the usual way of contemplating the most ordinary cat, you have a “bunch” of fifty light bulbs on the wires that respond to the irritability of the photosensitive receptors of the retina. Try now exclusively in terms of which of the lamps are burning and which are not, to formulate what a cat is. Isn't it true, when solving this problem, there is a desire to write down the sequence in which the mentioned lamps light up or go out. The process of creating such a record is already a germ (language for the translator: meant seed) of language methods.
Suppose, after watching the lamps for a while and reflecting, you gave an exhaustive definition of the concept "cat." Then the question of its universality would be natural: if someone else, having the same bunch of lamps, exhaustively defines what a cat is Do your definitions match? To clarify the situation, let's take a simple example. Imagine a bouquet of seven lamps reflecting the state of seven photosensitive receptors, arranged as in Figure 1a

If the lamps are exactly the same and there is no way to decide on any of them what is the location of the receptor associated with it, then in order to avoid confusion, it would be reasonable to mark each of these lamps with a number. In accordance with the numbering of Figure 1a, the figure, referred to here as the “black bone” (Fig. 1b), can be exhaustively described by simply enumerating which lamp numbers are on and those are not.
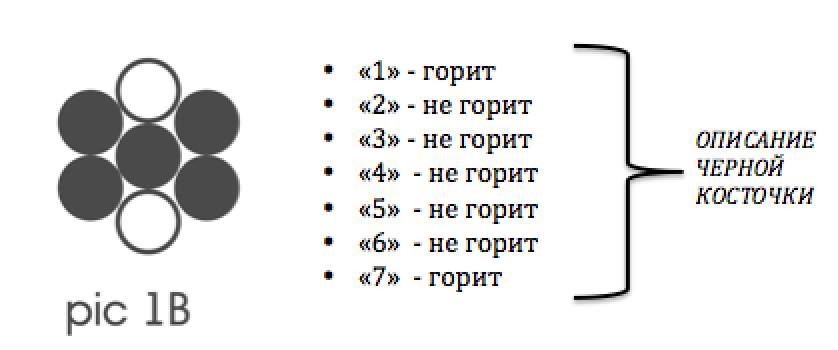
Unfortunately, such definitions of pits do not pretend to any universality, since there are no prerequisites for different people to number the lamps equally. This is a bit like the fact that even among similar-looking nationalities, the same concepts, for example the sun, have different names.
It is known that the eye of an insect consists of a multitude of independent small eyes, arranged like cells in bee cells. The obvious way of constructing the nature of the insect's view (this is only a reasonable guess) would be to associate with each such eye its own small intermediate brain section, the task of which would be to create a description of the current image on the retina of the eye and transfer this description to higher sections. In order for an insect to understand that different eyes are actually observing the same object and to track the position of this object, it would be highly preferable to have a method that allows intermediate sections for identical images to build the same descriptions, regardless of which eye of the retina such images appear (Fig.2).
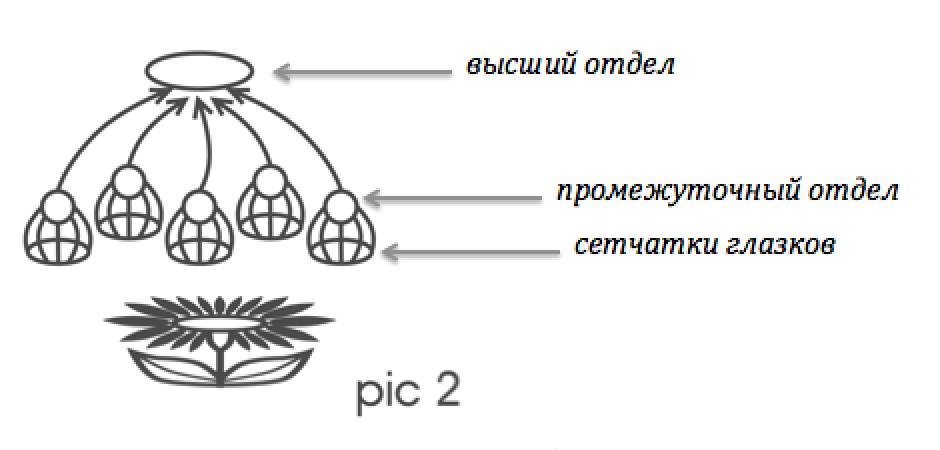
A similar method could be the description of images exclusively in geometric terms, devoid of correlation with any numbering. However, one should not forget that the definition of all these “geometrical terms” should be given in advance through all the same amorphous bouquets of lamps.
A related question to the problem just described is how a person’s process of recognizing the shape of color spots is arranged in such a way that it does not depend on the position of these spots in the field of view, and how to give the same opportunity to machines. Let some machine or a living organism be able to classify the shape of the color spots and their relative position. Is this enough for an opportunity to form concepts about places and objects? The key feature of places and objects is that it is impossible to observe them entirely, unlike color spots, no matter how you rotate the assembled Rubik's cube, you will not be able to see more than three of its faces at the same time. Everyone has an idea of their city or village, but there are probably many such places in them that cannot be seen at once.
In the first part of the nearest narration, an extremely simple example will show how to define basic geometric concepts in terms of color and motion receptors. The second part is devoted to symmetries and how the form can be determined in an invariant way with respect to the position in the field of view, and in the third - the means necessary for the formation of the concepts "object" and "place" are explored.
')
In order to illustrate how in the process of perception there appears an idea about the properties of a geometric character, let us take a fairly simple example from a perceived object, such properties in itself of the incumbent and the perceiver — able to notice them. These objects will serve us as a hexagonal lattice, painted in an arbitrary way in black and white, like a political map, and a probe from seven color-sensitive receptors connected by a frame capable of moving over this lattice.
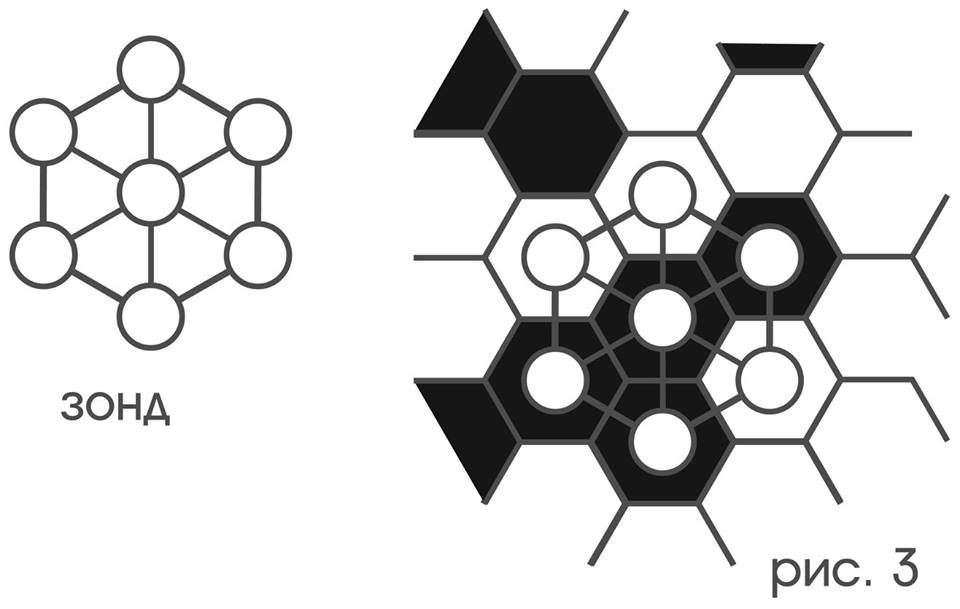
For the convenience of describing the movement of the probe, we rigidly associate it with the dial so that the receptors are opposite the “2”, “4”, ... “12” marks (Fig. 4).
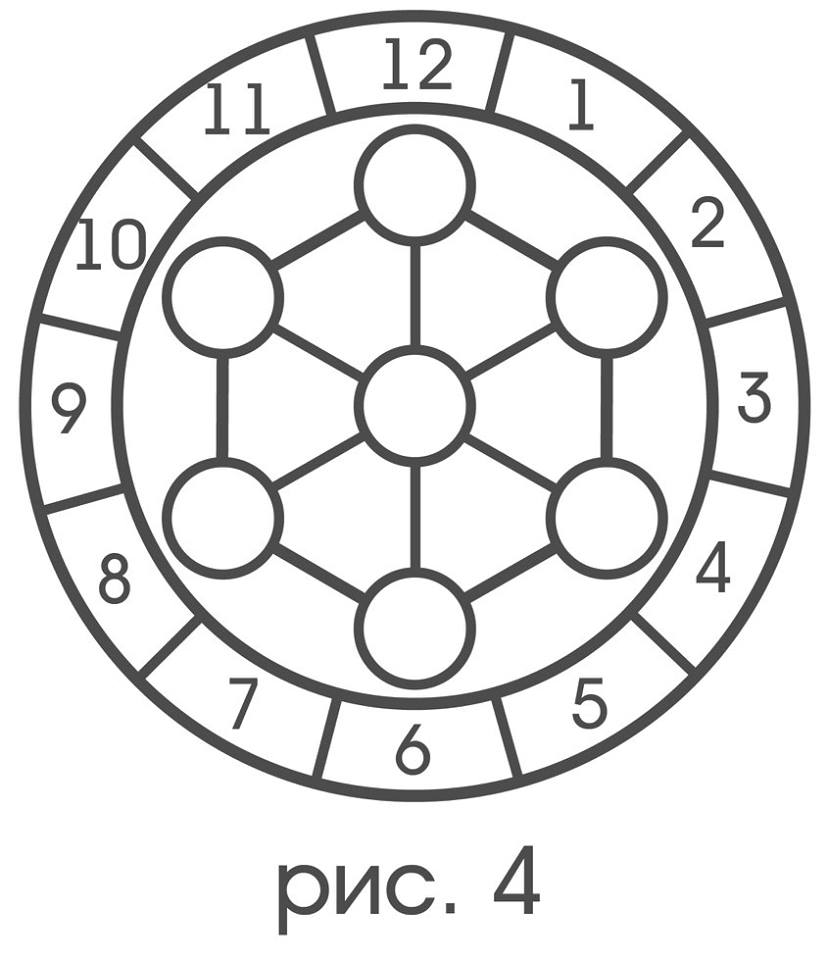
If this is done, then each instruction of the form: “displace the probe parallel to itself in the direction“ 2 ”by 6 cells, then rotate it one third turn counter-clockwise, then again displace in the direction“ 12 ”by 4 cells” define some type movements (it is believed that the dial rotates with the probe). Among these types, we emphasize plane-parallel displacements by one cell in the direction "2", "4" ... "12", for brevity, denoting them respectively as,, ... ↑, as well as turns around the central receptor by 60 ° clockwise - ↷ and against - ↶. The first will be called elementary displacements, and the second - elementary rotations. It is assumed that the probe is capable of instantaneously performing movements of certain types, among which elementary displacements are necessarily present, but not necessarily elementary rotations.
The movements of such types are called simple for the probe.
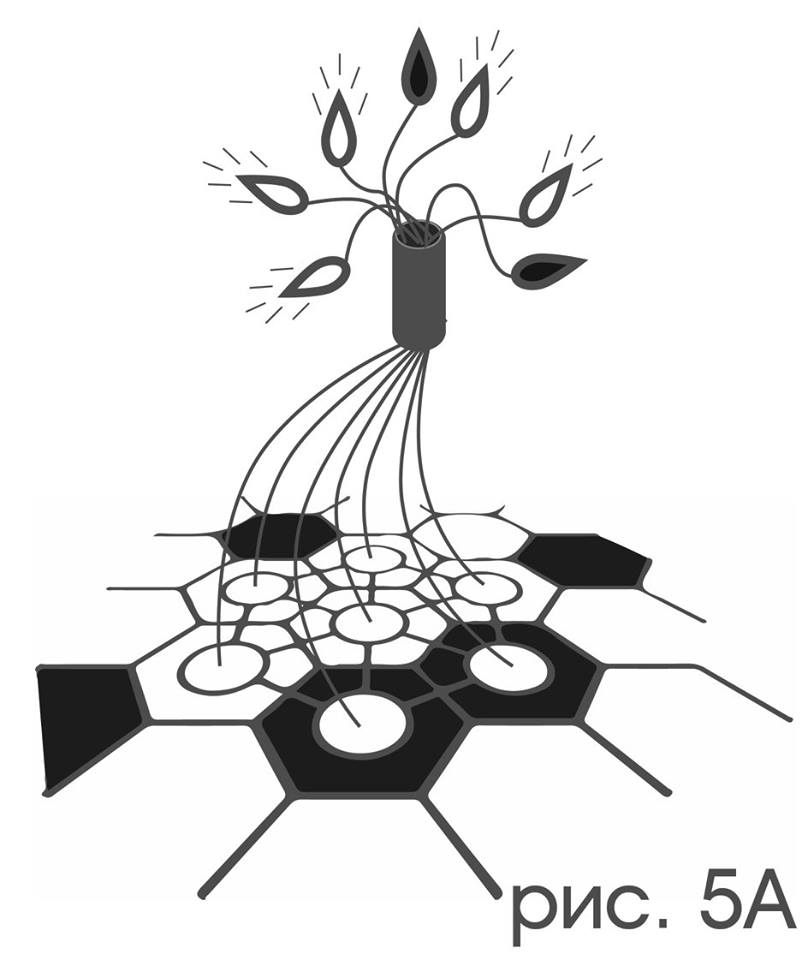
Following the general idea of the story, we will assume that the receptors are connected to the color-sensitive receptors in an arbitrary way, possibly not reflecting their mutual arrangement, a bunch of seven lamps of the same kind, each of which burns exactly when the receptor connected above it is above the white cell ( rice 5a).
Simple movements will be monitored with the help of another bouquet of lamps: each of its lamps goes out at those moments in which movements of the type represented by this lamp occur.
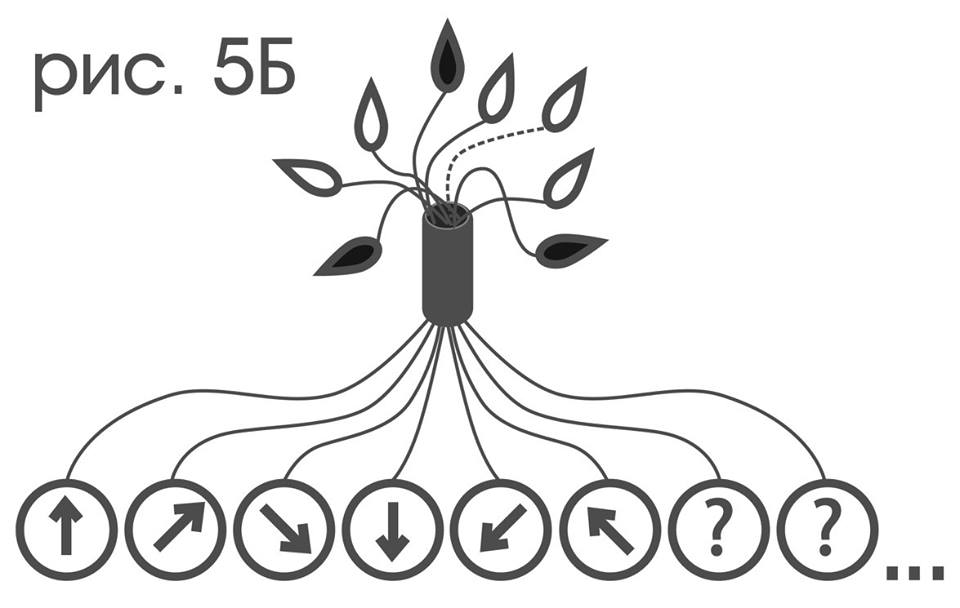
It also assumes the absence of any possibility only by the type of lamps to determine the types of movements represented by them. But can this be done in another way?
Socrates in one of the "Plato's Dialogues" noted that if only one artist lives in a village, the property of being an artist unequivocally calls this person or, the same thing, is categorical for him. The connection of the probe with the indicators gives rise to the following duality: any phenomenon observed in relation to the color-sensitive receptors and movements of the probe is dually a phenomenon observed in relation to its indicators; however, any regularity that can be formulated only in terms of movements and colors perceived by receptors, is dually consistent with a pattern that can be expressed only in terms of its indicators. Naturally, therefore, an attempt is so categorically to characterize which particular phenomena or which regularities correspond to each other, so that, observing only the indicators, be able to say what happens at this moment with the probe.
The transition from the definition of a certain concept to the definition of its dual concept will be called a translation. We will agree, wherever possible, to give identical names to dual concepts, while speaking about the proper meaning of these names, when they call concepts that relate directly to the probe, and the improper sense when it comes to phenomena associated with its indicators. As an illustration, we will try in dual terms to characterize the class of elementary displacements and the “be central” properties of the receptors.
There may be such a phenomenon that every time immediately after the completion of the p-type movement, the color-sensitive receptor x always appears above the same cell, over which the receptor y was directly above the execution of this movement.
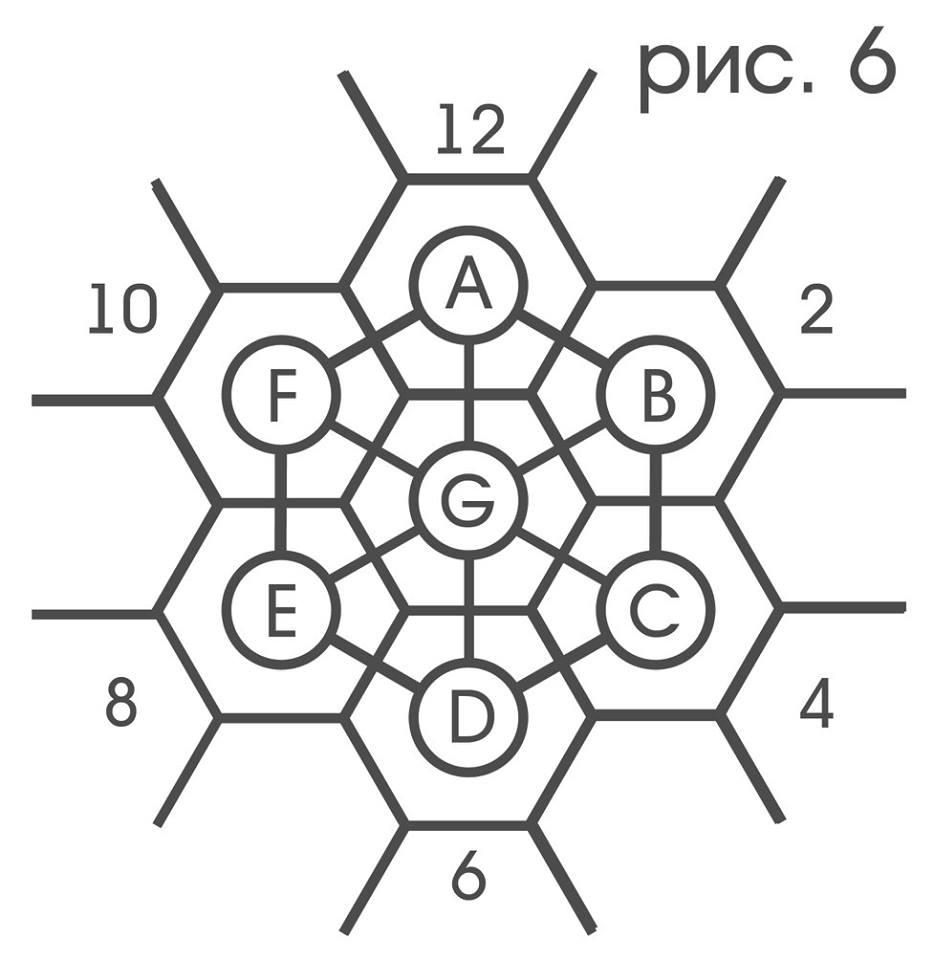
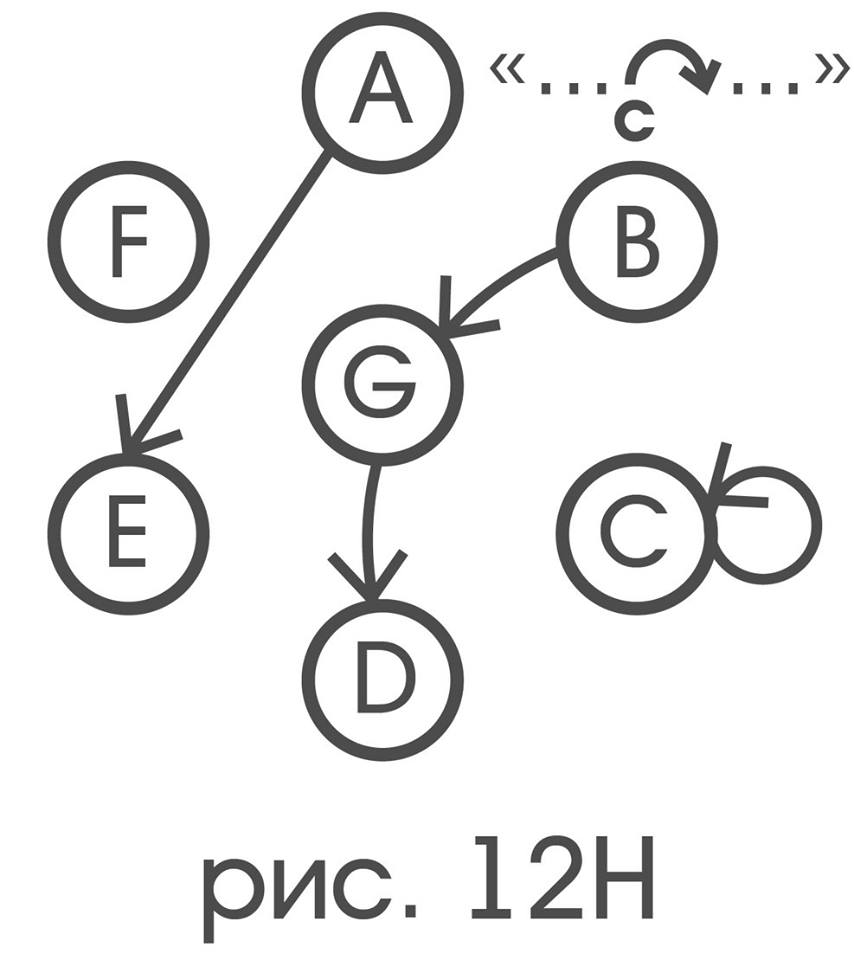
Let the receptors are labeled A, B, ... G as in Figure 6,
then G after the shift of ↑, always appears on the place where it was A;

E after double displacement by ➚ always appears on the place where B was before;
every time after turning around C by 60 ° in the clockwise direction, C remains in its place, and E is where A. was before.

Careful consideration of the above illustrations suggests that the same phenomenon can be defined without mentioning the lattice cells - exclusively in terms of receptors, types of movements and colors:
“Let us say that the receptor y lies in the direction of movement P from the receptor x, if every time after the completion of a movement of type P the color-sensitive receptor x perceives the same color that it perceived y immediately before performing this movement”.
On the other hand, as already noted, for any concept that is definable only in terms of receptors and types of movements, there is a dual concept to it, definable in terms of indicators. As for the concept of “lying in direction”, the dual to it has the following obvious wording:
"We will say that the color indicator y lies in the direction of movement determined by the indicator P from the indicator x, if every time immediately after the moment when the indicator P goes out, the indicator x is in the same state as y was just before the specified moment "
In accordance with these two definitions, the phrase “x lies in the direction P from y”, when instead of x and y some probe receptor names are substituted, and instead of P - the name of the type of its simple movements, it acquires its own meaning by describing the relationship between pairs of receptors and types of movements. When, instead of x and y, some names of color indicators are substituted, and instead of P, the name of the movement indicator, this phrase has an improper meaning and describes the relationship between pairs of color indicators and movement indicators. To abbreviate in both cases, instead of “x lies in the direction P from y”, we agree to write x (P) y.
We often talk about things without specifically naming them: “an unknown, robbing bank yesterday”, “a horse that will come in the first race tomorrow.” It is in this, purely narrative sense, that the phrases “indicator associated with receptor x” (abbreviated n [x]) and “indicator representing simple movements of type P” (abbreviated to n [P]) will be used for the time being without assuming the existence of any particular ways to find out which lamp is connected with x or represents P. In the notation introduced in this way, it can be stated that
G (↑) A and n [G] (n [↑]) n [A] (Fig.7)
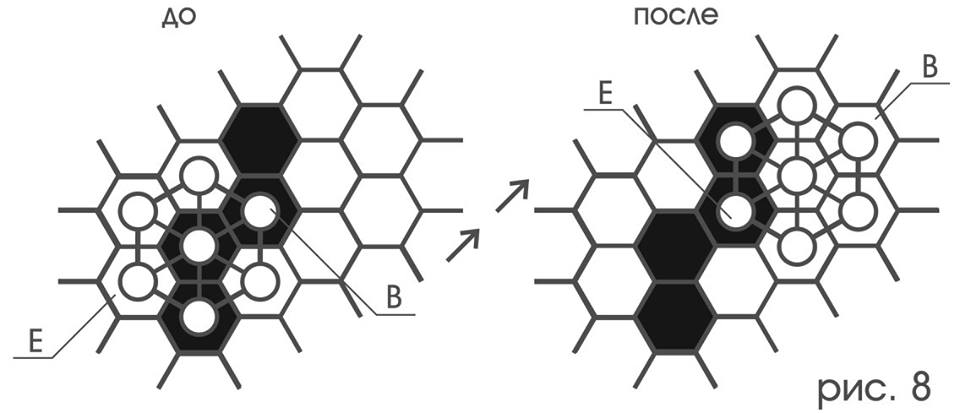
E (➚ * ➚) B and n [E] (n [➚ ➚]) n [B] (Fig.8)
C (↷_C) C and n [C] (n [↷_C]) n [C] (Fig.9)
E (_C) A and n [E] (n [↷_C]) n [A] (Fig.9)
Fixing any simple type of movement p gives a two-place relationship ... (p) ... on the set of color-sensitive receptors of the probe, while fixing the motion indicator q results in a two-place relationship ... (q) ... on many color indicators. Binary relations on sets are conveniently depicted as oriented graphs: to do this, you need to connect with arrows those elements of the set that are in this relation. To illustrate this, we take the set of numbers {1,2,3,4,5} and the relation “next in succession”, then it will be displayed as a graph:
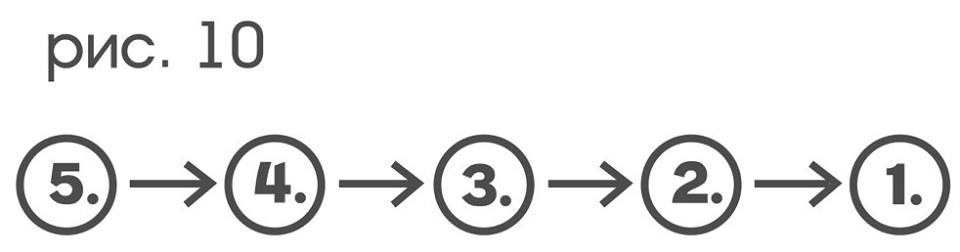
If the relation “to be less than” is taken on the same set, then its graph will be:
where, for example, an arrow from 2 to 4 means that 2 is less than 4.
The relationship graph “... (…) ...” (means: “...” in the direction of “...”) will be

the graph of his dual relationship “... (n [↑]) ...” is obtained by simply replacing the names of the receptors with the names of the indicators associated with them.
Below are graphs of several more relationships:
"... (↓) ..."
"... (➚) ..."
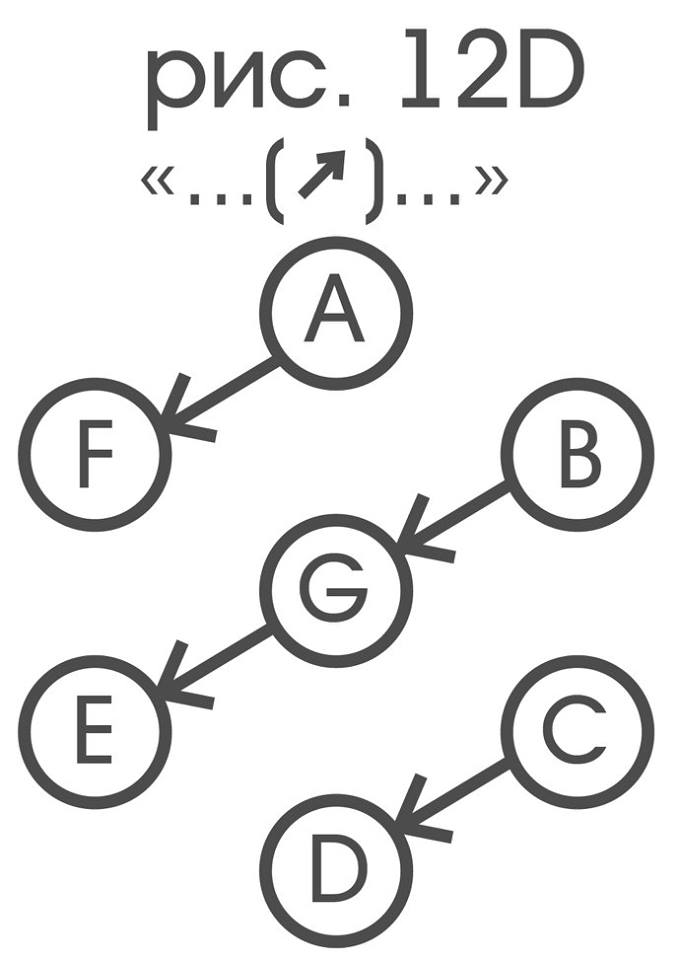
“...” lies in the direction of double displacement ➚ from “...”
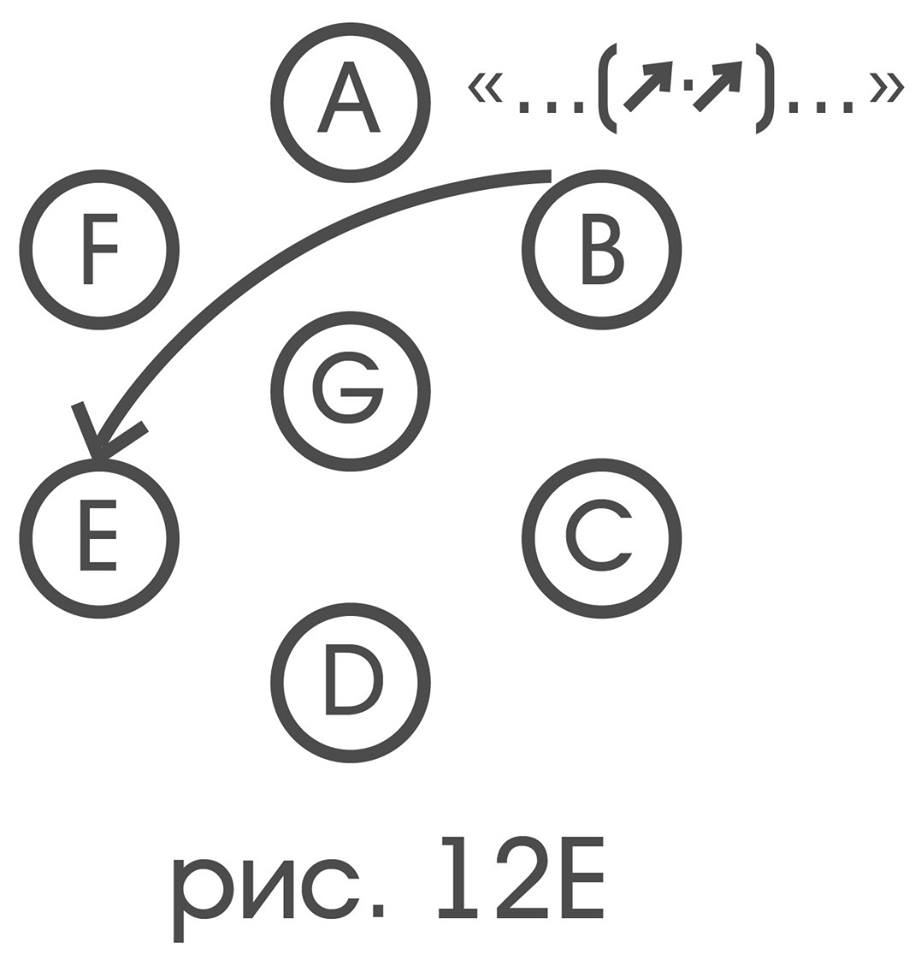
"... (↷) ..." ("..." lies in the direction of turning around G by 60 ° - clockwise from "...")
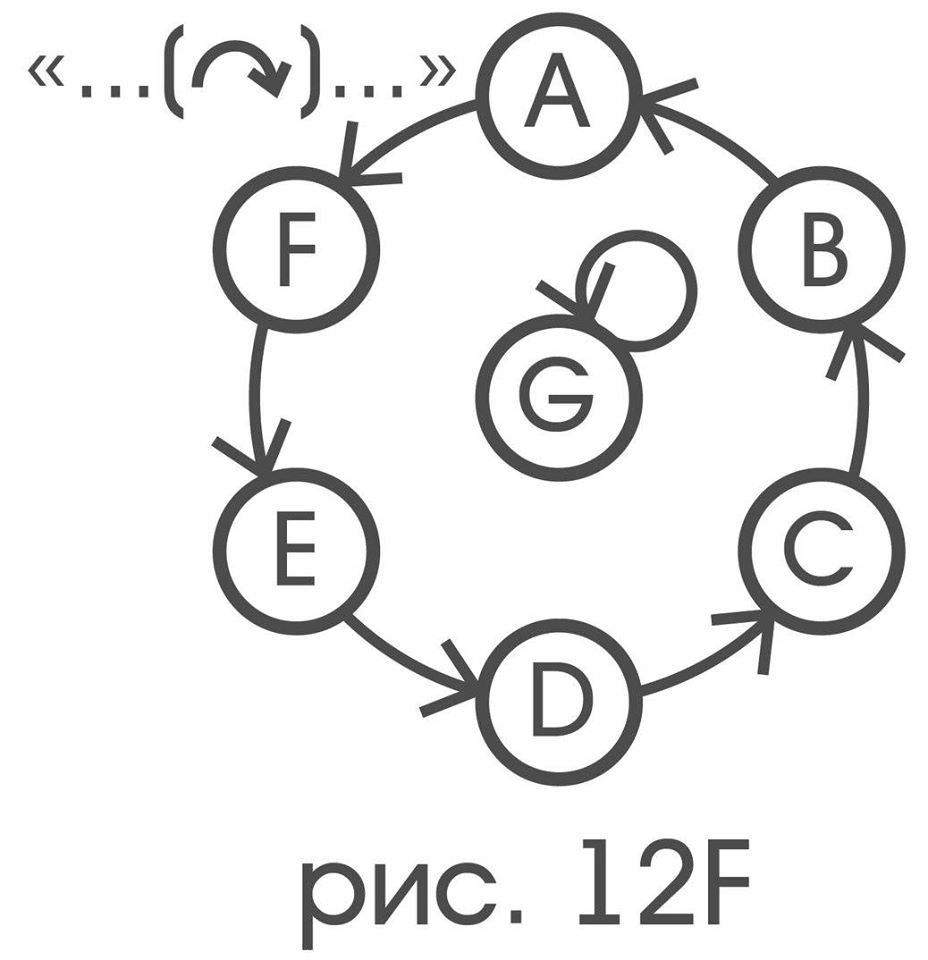
"... (↶ * ↶) ..." ("..." lies in the direction of turning around G by 120 ° - counterclockwise from "...")
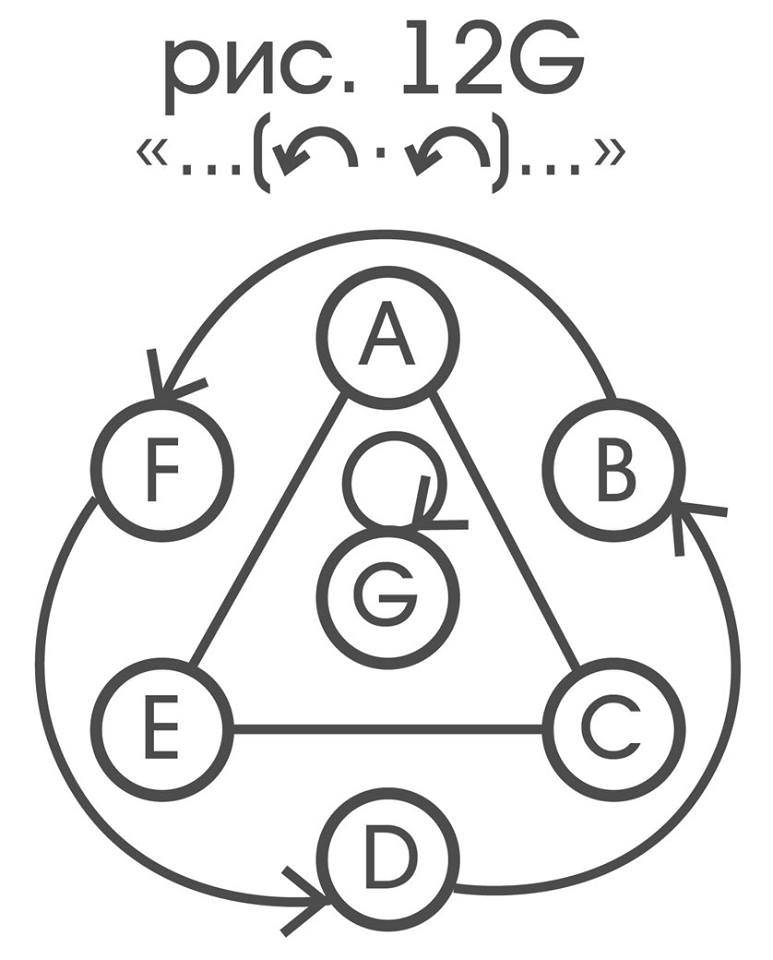
“... (↷_C) ...”
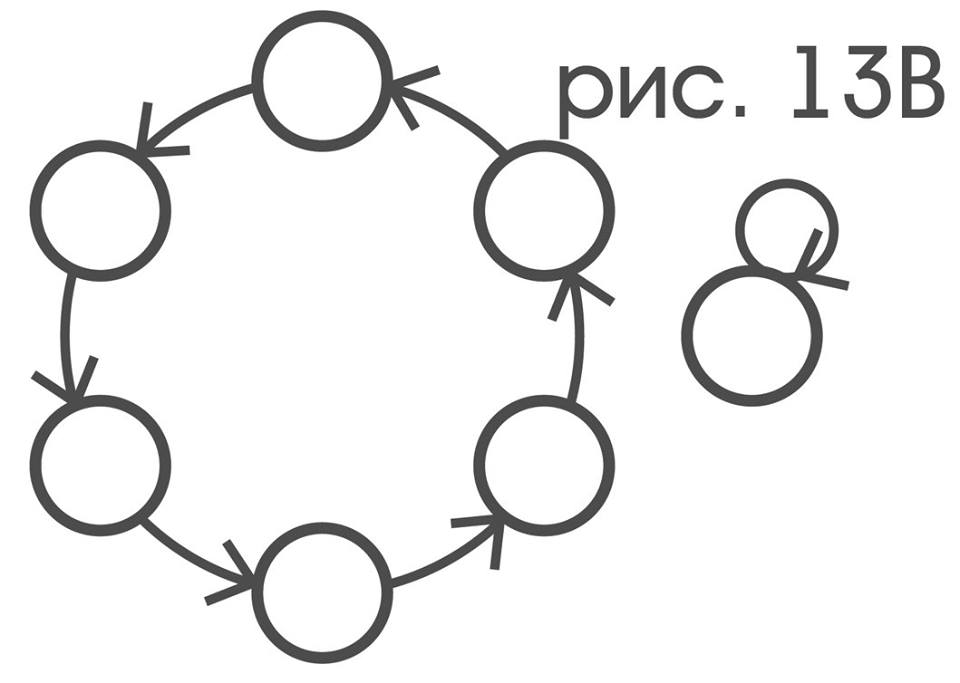
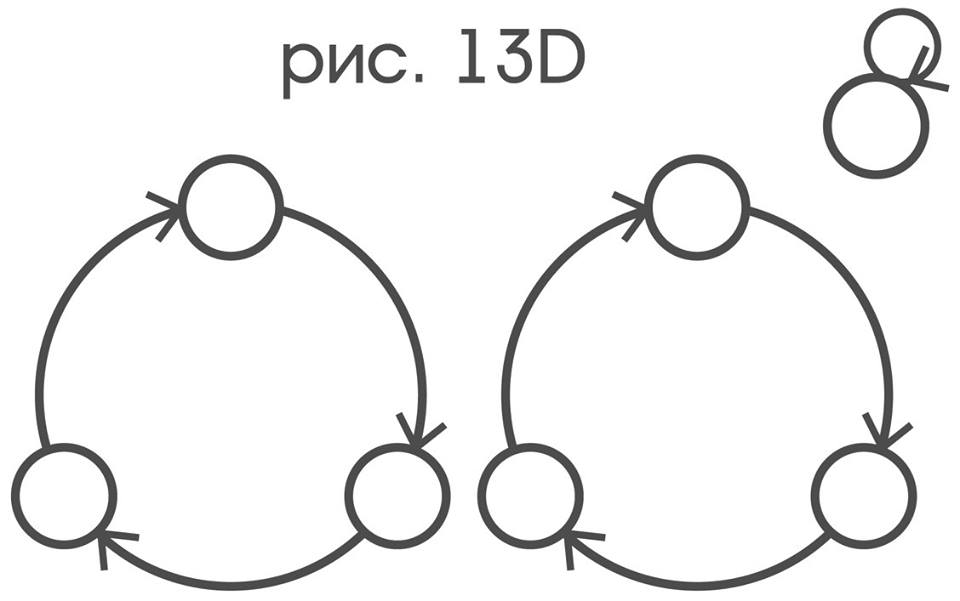
If now in the drawn graphs to erase the letters, it will turn out that it is natural to call them structures. The usual search can show that only elementary offsets correspond to the structure S:
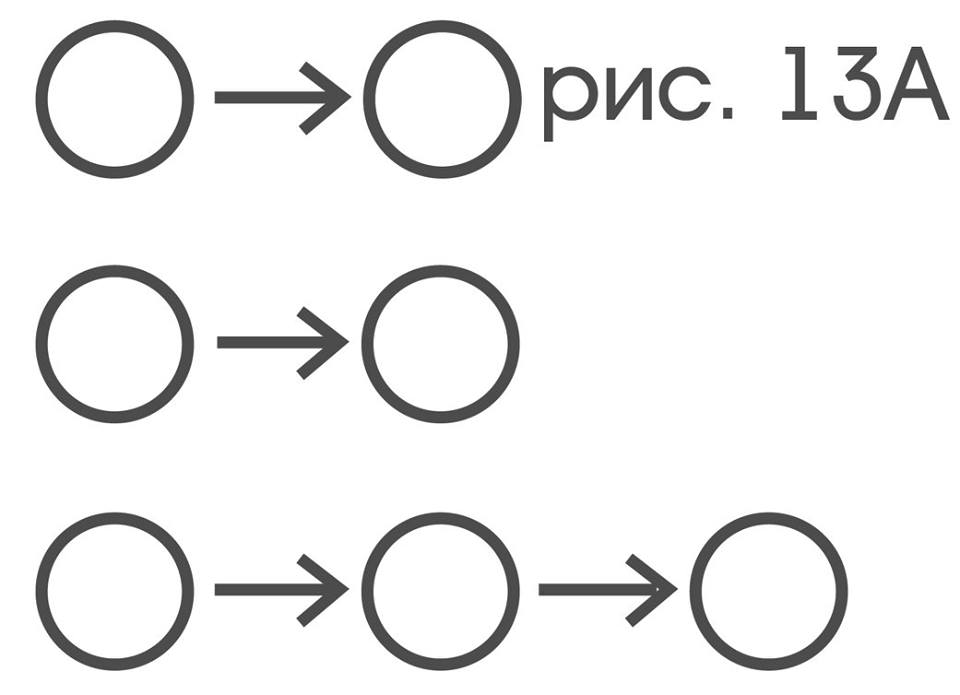
only elementary turns structure R:
just by turning 60 ° around the off-center receptor:
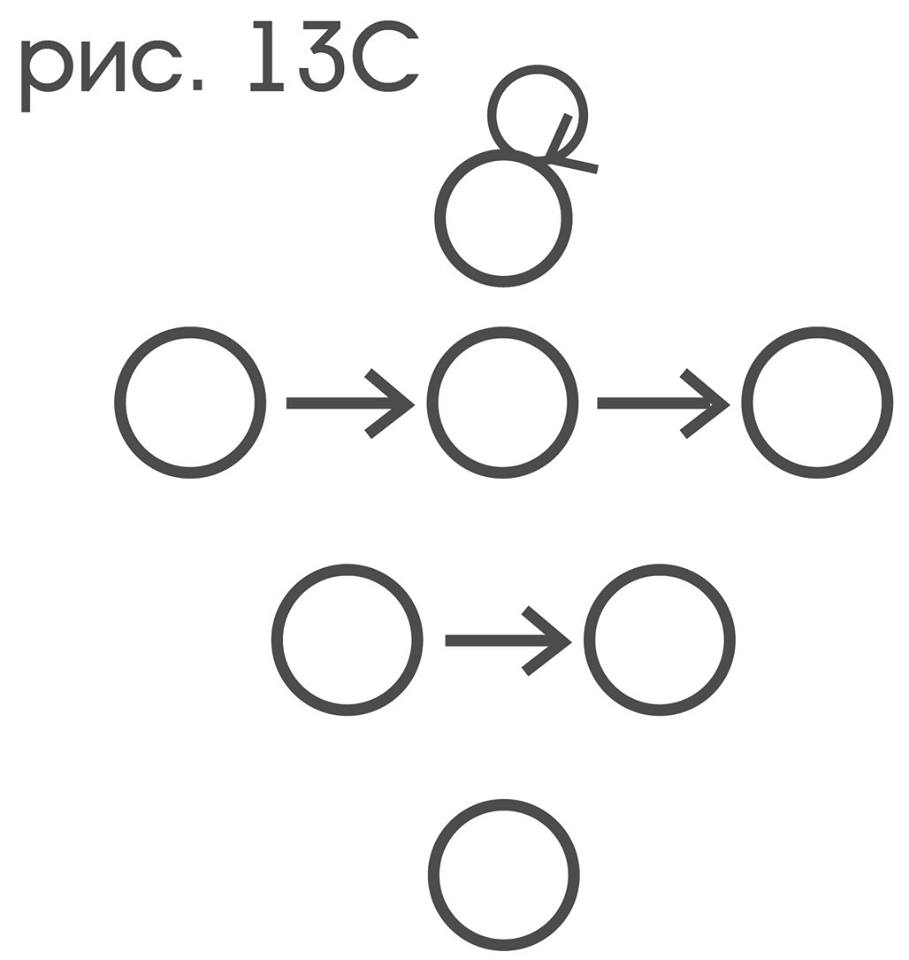
just by turning 120 ° around the central receptor:
only the movement that leaves the probe in place:
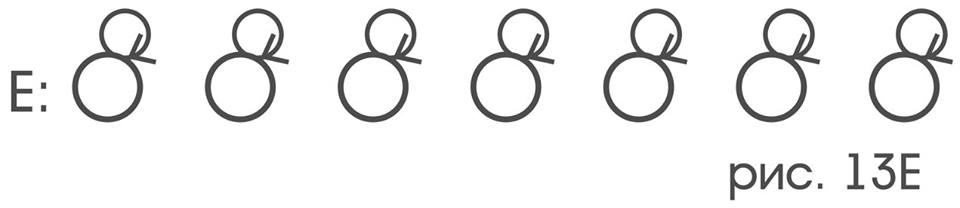
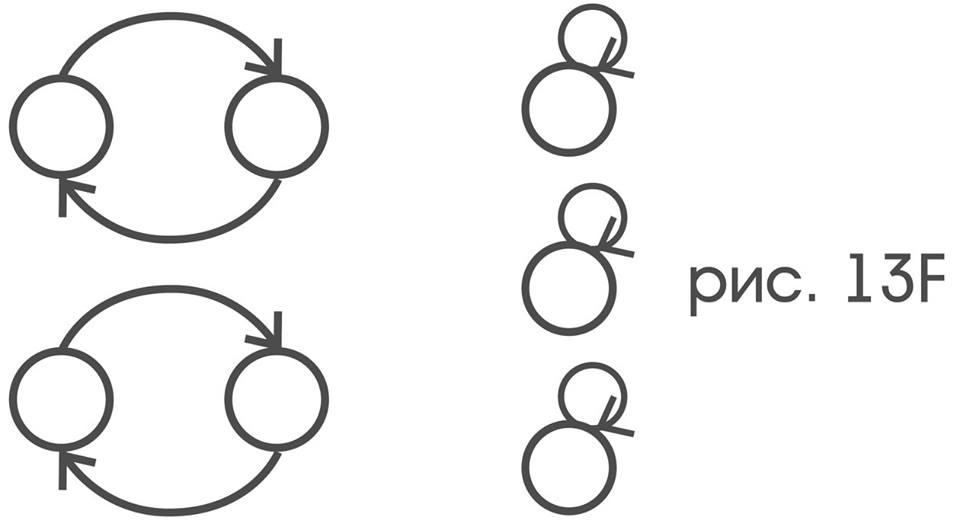
and only to movements that turn the probe like a coin, without displacing it
It should be obvious to the reader that if one graph is obtained from the other by simply renaming the vertices, then both of these graphs have the same structure. It is precisely by such an operation that the graphs of relations dual to each other are interconnected, which means that their structures must coincide. The last two remarks allow even without being able to see the probe itself, but solely by observing its indicators, for each movement indicator p decide whether the movement it represents is an elementary displacement or not. For this purpose, it is necessary to establish for which pairs of x and y color indicators the relation x (p) y is fulfilled and to draw its graph: p represents a certain elementary displacement exactly when the resulting graph has the structure S:

Thus, the phrase "p has the property that the relationship graph ... (p) ... has the structure S", if p is understood to mean the movement of the probe and the other terms are used in the proper sense, it defines the property "to be an elementary displacement", and if the terms are used in an intrinsic sense, the motion indicator property dual to it is “to represent an elementary displacement”.
Not all probe receptors are located equally relative to each other: among them there are six "peripheral" and one "central". Is there a way, without being able to see the probe itself, but only long enough watching its indicators, to determine which of the color indicators is associated with the central receptor, and which with the peripheral ones. To show the existence of this method, it suffices to find such a categorical property of the central receptor (as “being an artist”) that would allow translation into ambiguous terms. This translation must be a categorical property of the indicator that is associated with the central receptor.
The property “movement to be an elementary displacement” permits translation, the property “one receptor to lie in the direction of a given movement from another receptor” also permits translation. With respect to the “central” receptor, the property x will be categorical: “if the movement p is an elementary displacement, then the receptor x lies both in the direction p from some receptor, and some receptor lies in the direction p from x”. The last expression, as the composition is translatable, also turns out to be translatable.
Part 2
Sergey Kovalenko
Dubna 2015
Part 3
Introduction (The linguistic nature of abstract concepts)
The purpose of this work is to show how languages like English, as a natural and effective method, can arise at different levels of the process of perception. Along the way, the issues of mechanisms that allow us and animals to see, classify color spots by shape, get an idea of places, objects and their geometric properties are touched upon. A few words are devoted to purely linguistic problems: which concepts and methods should be present in any sufficiently expressive descriptive language among the initial ones, and which, as derivatives, can be derived from the initial ones.
How could language participate, for example, in the process of visual perception? Each of us is used to talking about our ability to see a tree, to hear the birds singing and to feel warmly, holding our hand over a candle. Yet our To consciousness, neither sound, nor heat, nor the sensation of light is directly accessible to perception. The idea of all this is formed solely on the basis of the properties and patterns of irritation of our recipes. To understand the complexity of the tasks arising in such cases before the brain, imagine that, instead of the usual way of contemplating the most ordinary cat, you have a “bunch” of fifty light bulbs on the wires that respond to the irritability of the photosensitive receptors of the retina. Try now exclusively in terms of which of the lamps are burning and which are not, to formulate what a cat is. Isn't it true, when solving this problem, there is a desire to write down the sequence in which the mentioned lamps light up or go out. The process of creating such a record is already a germ (language for the translator: meant seed) of language methods.
Suppose, after watching the lamps for a while and reflecting, you gave an exhaustive definition of the concept "cat." Then the question of its universality would be natural: if someone else, having the same bunch of lamps, exhaustively defines what a cat is Do your definitions match? To clarify the situation, let's take a simple example. Imagine a bouquet of seven lamps reflecting the state of seven photosensitive receptors, arranged as in Figure 1a

If the lamps are exactly the same and there is no way to decide on any of them what is the location of the receptor associated with it, then in order to avoid confusion, it would be reasonable to mark each of these lamps with a number. In accordance with the numbering of Figure 1a, the figure, referred to here as the “black bone” (Fig. 1b), can be exhaustively described by simply enumerating which lamp numbers are on and those are not.

Unfortunately, such definitions of pits do not pretend to any universality, since there are no prerequisites for different people to number the lamps equally. This is a bit like the fact that even among similar-looking nationalities, the same concepts, for example the sun, have different names.
It is known that the eye of an insect consists of a multitude of independent small eyes, arranged like cells in bee cells. The obvious way of constructing the nature of the insect's view (this is only a reasonable guess) would be to associate with each such eye its own small intermediate brain section, the task of which would be to create a description of the current image on the retina of the eye and transfer this description to higher sections. In order for an insect to understand that different eyes are actually observing the same object and to track the position of this object, it would be highly preferable to have a method that allows intermediate sections for identical images to build the same descriptions, regardless of which eye of the retina such images appear (Fig.2).

A similar method could be the description of images exclusively in geometric terms, devoid of correlation with any numbering. However, one should not forget that the definition of all these “geometrical terms” should be given in advance through all the same amorphous bouquets of lamps.
A related question to the problem just described is how a person’s process of recognizing the shape of color spots is arranged in such a way that it does not depend on the position of these spots in the field of view, and how to give the same opportunity to machines. Let some machine or a living organism be able to classify the shape of the color spots and their relative position. Is this enough for an opportunity to form concepts about places and objects? The key feature of places and objects is that it is impossible to observe them entirely, unlike color spots, no matter how you rotate the assembled Rubik's cube, you will not be able to see more than three of its faces at the same time. Everyone has an idea of their city or village, but there are probably many such places in them that cannot be seen at once.
In the first part of the nearest narration, an extremely simple example will show how to define basic geometric concepts in terms of color and motion receptors. The second part is devoted to symmetries and how the form can be determined in an invariant way with respect to the position in the field of view, and in the third - the means necessary for the formation of the concepts "object" and "place" are explored.
')
Geometric concepts of hexagonal lattice
In order to illustrate how in the process of perception there appears an idea about the properties of a geometric character, let us take a fairly simple example from a perceived object, such properties in itself of the incumbent and the perceiver — able to notice them. These objects will serve us as a hexagonal lattice, painted in an arbitrary way in black and white, like a political map, and a probe from seven color-sensitive receptors connected by a frame capable of moving over this lattice.

For the convenience of describing the movement of the probe, we rigidly associate it with the dial so that the receptors are opposite the “2”, “4”, ... “12” marks (Fig. 4).

If this is done, then each instruction of the form: “displace the probe parallel to itself in the direction“ 2 ”by 6 cells, then rotate it one third turn counter-clockwise, then again displace in the direction“ 12 ”by 4 cells” define some type movements (it is believed that the dial rotates with the probe). Among these types, we emphasize plane-parallel displacements by one cell in the direction "2", "4" ... "12", for brevity, denoting them respectively as,, ... ↑, as well as turns around the central receptor by 60 ° clockwise - ↷ and against - ↶. The first will be called elementary displacements, and the second - elementary rotations. It is assumed that the probe is capable of instantaneously performing movements of certain types, among which elementary displacements are necessarily present, but not necessarily elementary rotations.
The movements of such types are called simple for the probe.
Following the general idea of the story, we will assume that the receptors are connected to the color-sensitive receptors in an arbitrary way, possibly not reflecting their mutual arrangement, a bunch of seven lamps of the same kind, each of which burns exactly when the receptor connected above it is above the white cell ( rice 5a).

Simple movements will be monitored with the help of another bouquet of lamps: each of its lamps goes out at those moments in which movements of the type represented by this lamp occur.

It also assumes the absence of any possibility only by the type of lamps to determine the types of movements represented by them. But can this be done in another way?
Socrates in one of the "Plato's Dialogues" noted that if only one artist lives in a village, the property of being an artist unequivocally calls this person or, the same thing, is categorical for him. The connection of the probe with the indicators gives rise to the following duality: any phenomenon observed in relation to the color-sensitive receptors and movements of the probe is dually a phenomenon observed in relation to its indicators; however, any regularity that can be formulated only in terms of movements and colors perceived by receptors, is dually consistent with a pattern that can be expressed only in terms of its indicators. Naturally, therefore, an attempt is so categorically to characterize which particular phenomena or which regularities correspond to each other, so that, observing only the indicators, be able to say what happens at this moment with the probe.
The transition from the definition of a certain concept to the definition of its dual concept will be called a translation. We will agree, wherever possible, to give identical names to dual concepts, while speaking about the proper meaning of these names, when they call concepts that relate directly to the probe, and the improper sense when it comes to phenomena associated with its indicators. As an illustration, we will try in dual terms to characterize the class of elementary displacements and the “be central” properties of the receptors.
There may be such a phenomenon that every time immediately after the completion of the p-type movement, the color-sensitive receptor x always appears above the same cell, over which the receptor y was directly above the execution of this movement.
Let the receptors are labeled A, B, ... G as in Figure 6,

then G after the shift of ↑, always appears on the place where it was A;

E after double displacement by ➚ always appears on the place where B was before;

every time after turning around C by 60 ° in the clockwise direction, C remains in its place, and E is where A. was before.

Careful consideration of the above illustrations suggests that the same phenomenon can be defined without mentioning the lattice cells - exclusively in terms of receptors, types of movements and colors:
“Let us say that the receptor y lies in the direction of movement P from the receptor x, if every time after the completion of a movement of type P the color-sensitive receptor x perceives the same color that it perceived y immediately before performing this movement”.
On the other hand, as already noted, for any concept that is definable only in terms of receptors and types of movements, there is a dual concept to it, definable in terms of indicators. As for the concept of “lying in direction”, the dual to it has the following obvious wording:
"We will say that the color indicator y lies in the direction of movement determined by the indicator P from the indicator x, if every time immediately after the moment when the indicator P goes out, the indicator x is in the same state as y was just before the specified moment "
In accordance with these two definitions, the phrase “x lies in the direction P from y”, when instead of x and y some probe receptor names are substituted, and instead of P - the name of the type of its simple movements, it acquires its own meaning by describing the relationship between pairs of receptors and types of movements. When, instead of x and y, some names of color indicators are substituted, and instead of P, the name of the movement indicator, this phrase has an improper meaning and describes the relationship between pairs of color indicators and movement indicators. To abbreviate in both cases, instead of “x lies in the direction P from y”, we agree to write x (P) y.
We often talk about things without specifically naming them: “an unknown, robbing bank yesterday”, “a horse that will come in the first race tomorrow.” It is in this, purely narrative sense, that the phrases “indicator associated with receptor x” (abbreviated n [x]) and “indicator representing simple movements of type P” (abbreviated to n [P]) will be used for the time being without assuming the existence of any particular ways to find out which lamp is connected with x or represents P. In the notation introduced in this way, it can be stated that
G (↑) A and n [G] (n [↑]) n [A] (Fig.7)
E (➚ * ➚) B and n [E] (n [➚ ➚]) n [B] (Fig.8)
C (↷_C) C and n [C] (n [↷_C]) n [C] (Fig.9)
E (_C) A and n [E] (n [↷_C]) n [A] (Fig.9)
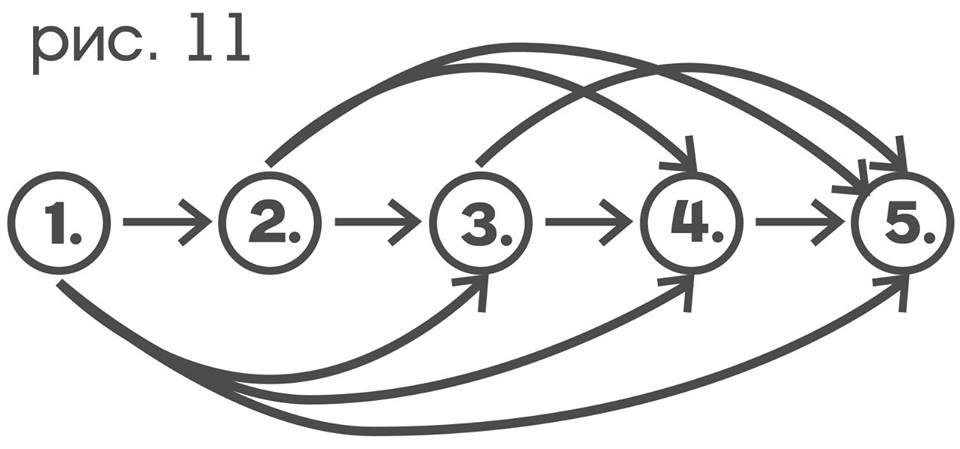
Fixing any simple type of movement p gives a two-place relationship ... (p) ... on the set of color-sensitive receptors of the probe, while fixing the motion indicator q results in a two-place relationship ... (q) ... on many color indicators. Binary relations on sets are conveniently depicted as oriented graphs: to do this, you need to connect with arrows those elements of the set that are in this relation. To illustrate this, we take the set of numbers {1,2,3,4,5} and the relation “next in succession”, then it will be displayed as a graph:

If the relation “to be less than” is taken on the same set, then its graph will be:

where, for example, an arrow from 2 to 4 means that 2 is less than 4.
The relationship graph “... (…) ...” (means: “...” in the direction of “...”) will be

the graph of his dual relationship “... (n [↑]) ...” is obtained by simply replacing the names of the receptors with the names of the indicators associated with them.

Below are graphs of several more relationships:
"... (↓) ..."

"... (➚) ..."

“...” lies in the direction of double displacement ➚ from “...”

"... (↷) ..." ("..." lies in the direction of turning around G by 60 ° - clockwise from "...")

"... (↶ * ↶) ..." ("..." lies in the direction of turning around G by 120 ° - counterclockwise from "...")

“... (↷_C) ...”

If now in the drawn graphs to erase the letters, it will turn out that it is natural to call them structures. The usual search can show that only elementary offsets correspond to the structure S:
only elementary turns structure R:

just by turning 60 ° around the off-center receptor:

just by turning 120 ° around the central receptor:

only the movement that leaves the probe in place:
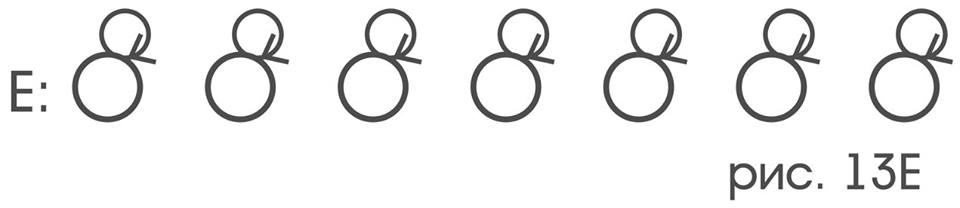
and only to movements that turn the probe like a coin, without displacing it

It should be obvious to the reader that if one graph is obtained from the other by simply renaming the vertices, then both of these graphs have the same structure. It is precisely by such an operation that the graphs of relations dual to each other are interconnected, which means that their structures must coincide. The last two remarks allow even without being able to see the probe itself, but solely by observing its indicators, for each movement indicator p decide whether the movement it represents is an elementary displacement or not. For this purpose, it is necessary to establish for which pairs of x and y color indicators the relation x (p) y is fulfilled and to draw its graph: p represents a certain elementary displacement exactly when the resulting graph has the structure S:

Thus, the phrase "p has the property that the relationship graph ... (p) ... has the structure S", if p is understood to mean the movement of the probe and the other terms are used in the proper sense, it defines the property "to be an elementary displacement", and if the terms are used in an intrinsic sense, the motion indicator property dual to it is “to represent an elementary displacement”.
Not all probe receptors are located equally relative to each other: among them there are six "peripheral" and one "central". Is there a way, without being able to see the probe itself, but only long enough watching its indicators, to determine which of the color indicators is associated with the central receptor, and which with the peripheral ones. To show the existence of this method, it suffices to find such a categorical property of the central receptor (as “being an artist”) that would allow translation into ambiguous terms. This translation must be a categorical property of the indicator that is associated with the central receptor.
The property “movement to be an elementary displacement” permits translation, the property “one receptor to lie in the direction of a given movement from another receptor” also permits translation. With respect to the “central” receptor, the property x will be categorical: “if the movement p is an elementary displacement, then the receptor x lies both in the direction p from some receptor, and some receptor lies in the direction p from x”. The last expression, as the composition is translatable, also turns out to be translatable.
Part 2
Sergey Kovalenko
Dubna 2015
Source: https://habr.com/ru/post/282081/
All Articles