On the development of non-paged keys based on passwords
Cryptographic protocols are the foundation of a secure network connection and confidential information exchange. Today there are a large number of various protocols for various purposes. Many of these protocols (for example, TLS, Kerberos) are heard even among people who are not closely connected with cryptography. They are ubiquitous and often have long been part of popular information systems.
However, there is a type of protocols that has recently gained increasing popularity, but is still not widely known - shared key generation protocols with password-based authentication. These protocols include the Russian protocol SESPAKE (Security Evaluated Standardized Password Authenticated Key Exchange), with the advent of which in Russia it became necessary to consider the features of protocols of this type. The purpose of this article is rather not to give another formal description of the new protocol, but to help the reader grasp its main idea and features and understand why there are certain steps in it, why they are important, and how this protocol class differs from everything previously known. .
In 1976, Whitfield Diffie and Martin Hellman proposed a simple but ingenious idea of ​​developing a common secret key — the well-known Diffie-Hellman protocol.
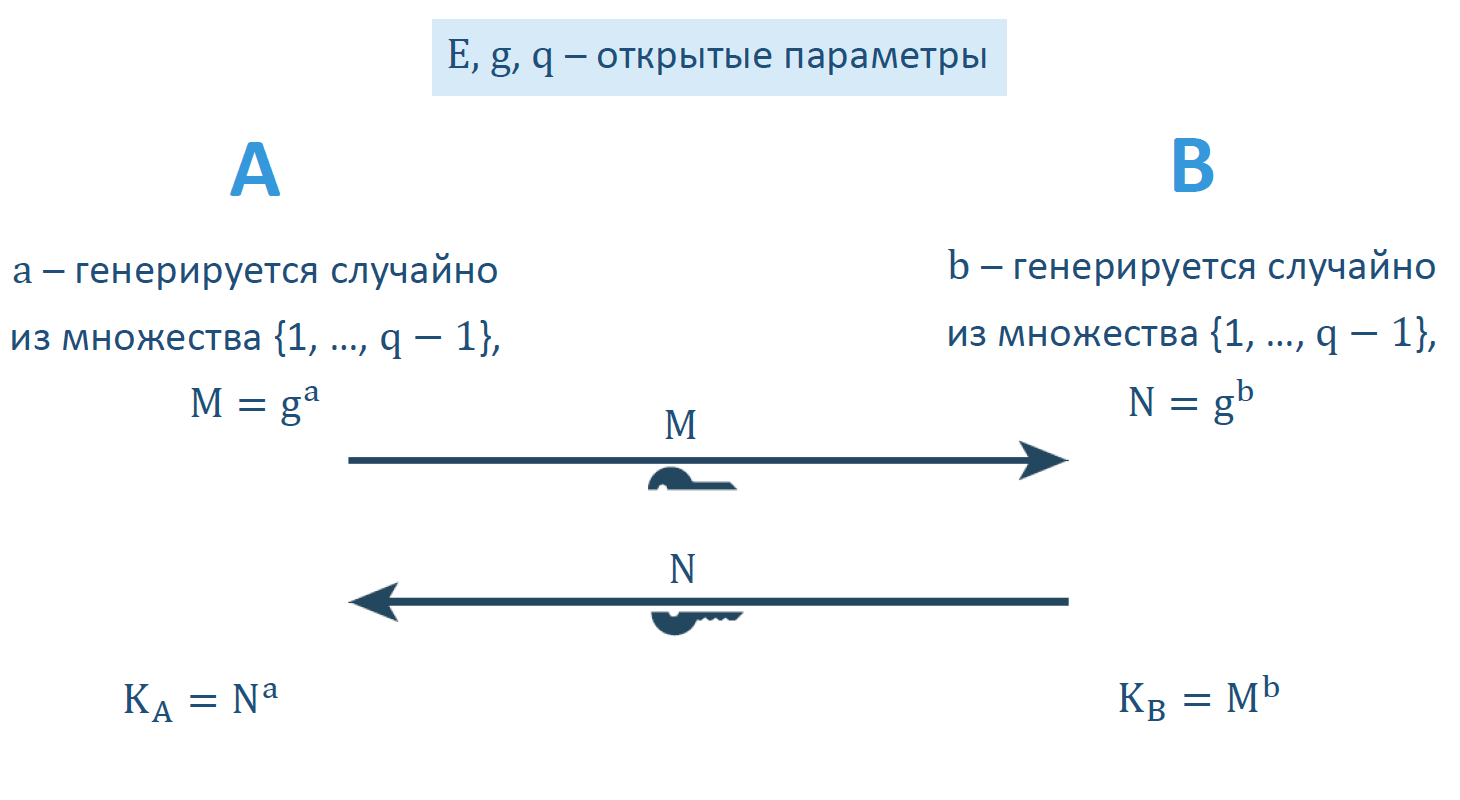
Here
- some finite multiplicative group , 
- her order, 
- the generating element of this group. Meanings 
and 
- public keys transmitted over an open communication channel, 
- key generated during the execution of the protocol.
')
The durability of this protocol with respect to the passive adversary is based on the so-called CDH problem, which is considered computationally “complex” (if we speak informally, then there are no effective solution algorithms for such a task). The formulation of this problem is as follows: knowing the values
, 
, calculate the value 
.
Unfortunately, the Diffie-Hellman protocol has one fundamental flaw: it is not secure if there is an active opponent in the transmission channel (see the “Man in the Middle” attack). The reason for this vulnerability lies in the absence of an authentication mechanism, i.e. during the protocol, the parties are not able to verify in any way that the shared key is developed together with the honest subscriber.
To date, several solutions have been proposed for this problem, here are some of them: the use of certificates and CAs , the introduction of a third trusted participant in the protocol or the use of a previously agreed secret. The latter approach is the simplest solution in terms of implementation. However, if the protocol involves the use of a secret, which is a long bit string, which is difficult for a person to remember, then there is the problem of keeping this secret safe.
The question arises, can we use a short and easily remembered password as a secret ? As soon as the word “password” appears, many people almost reflexively want to say that a priori cannot be achieved a priori, because The password can be quickly recovered by simple brute force or dictionary. It will be shown below that this is not always the case.
To begin with, consider the following key generation scheme, in which an authentication stage is added to the Diffie-Hellman protocol using a secret value:
Here
- some hash function 
- secret pre-agreed value, 
, 
- information used for authentication. It is easy to notice that the secret It is not used at all at the stage of generating a common key.
Why is this example bad in the case when is a regular password? As a rule, a password is a low-entropy value (that is, it consists of 4-6 characters, for example, a PIN), therefore, the enumeration of all possible values ​​of a password is quite an achievable task for the opponent. Therefore, a fundamental requirement for protocols using a short password is resistance to the so-called offline dictionary attack . This property should be achieved due to the fact that the information that can be obtained by both the passive and active adversary during the execution of the protocol does not provide a criterion for rejecting incorrect passwords in offline mode, i.e. For us, the ideal option is when an adversary cannot find a password by iterating through all possible values, the number of which is small, without user interaction. Returning to the example, let us ask ourselves the question: solving the problem of authentication, do not we give the enemy the criterion for rejecting the password ? To answer it, consider the following attack:
In this example, the opponent acts as follows: he replaces the side
and interacts with the party 
honestly following the protocol. Opponent generates common with key 
. He then receives from the subject authentication information )
, which depends on only one unknown parameter - low-entropy password . Therefore, the adversary receives the criterion for rejecting the wrong passwords.
However, if the use of a password were directly embedded in the generation of a key (which was an inseparable process from its development), the adversary would be able to receive a common key , just guessing the password during the interaction, then this attack would not be applicable, since he would have to go through not only the password, but also a long key.
This idea formed the basis of a new approach, namely the common key generation with password-based authentication ( PAKE ).
The first protocol of the PAKE type was proposed back in 1992 by Stephen Bellinow and Michael Merritt. This protocol assumed that to solve the authentication problem, subjects wishing to generate a common key use some easy-to-remember password known only to them. The main difference between PAKE protocols and the example considered above is the fact that the password is already used during the generation of the shared key.
In this case, the main requirements for such a protocol are:
Let us try to understand whether it is difficult to build such a protocol and what features it should have. To do this, consider the simplest example — the prototype of the PAKE protocol:
The blue here highlights the differences from the Diffie-Hellman protocol,
- one more generating element of the group .
Let's see if such a scheme is vulnerable to an offline dictionary attack. Values ​​are available to the passive adversary listening to the transmission channel
and 
- Diffie-Hellman public keys disguised as 
and authentication information and . Going through passwords, he can “remove” masks from values and , while obtaining the estimated values 
and 
. But an adversary can get a criterion for sorting passwords only if he can solve the computationally “complex” CDH problem for unmasked values. and i.e. by values and get the key 
(the criterion of the correctness of the password is to obtain the correct authentication information )
on a test key 
).
In the case of an active enemy, this scheme still has certain vulnerabilities. Consider the following attack on the scheme, where the discrete logarithms of one generating element relative to another are known. For simplicity, consider the case when
.
As in the previous attack, here the enemy simply replaces the side . Since he knows the key generation function, which depends only on one unknown parameter - a low-entropy password 
, he gets the opportunity to find the password by brute force, substituting the test key in the function of generating authentication information 
.
It is easy to see that a similar attack can be carried out even if the protocol uses different generating elements, but the discrete logarithm of one at the base of the other is known. In this case, the value of this logarithm will appear in the chain of equalities simply as some constant.
If we use different generating elements, such that the discrete logarithms of the one relative to the other are not known, we will not be able to get the key as a function only from an unknown password. Really,%5Ee%2F(h%5E%7BPW%7D)%5Ea)
where 
- high entropy unknown quantity.
To obtain such elements, it is necessary not only to generate them at random, but also to be able to convince everyone else that when they were generated, everything was purely random. This can be achieved if we choose the generating elements according to the principle of provable pseudo-randomness . So, for a multiplicative group of a finite field)
we can give the following algorithm for generating generators:
It would seem that now we have considered all potentially dangerous situations, however, when creating a protocol, it is necessary to take into account more complex issues. Any specialist who develops a new protocol knows that one of the most important requirements for such protocols is to provide them with the so-called implicit authentication of the key generated.
For us, this requirement means that the protocol we are designing must provide a cryptographically strong public key that meets the requirement of implicit authentication, even if we use the protocol without an explicit authentication stage. Let us return to our prototype and see if it satisfies this property.
Consider an attack in such an enemy model, where:
Despite the fact that we use different generating elements, if the enemy knows
and 
then knowing and 
, he can find the password value using the criterion %5E%7B-r%7D%20%3DN%2Fh%5E%7BPW%7D)
. Thus, by intercepting and replacing the message, he will actually be able to get the criteria for finding the password.
You can get rid of this vulnerability by using the hash function in the protocol:
Indeed, since a hash function that satisfies the cryptographic requirements is considered an analog of a pseudo-random function, there are no simple dependencies between its output and input that can be efficiently exploited. Thus, the opponent no longer has the criterion for finding the password and the attack ceases to be applicable.
So, we were able to build the simplest prototype of the generation of non-punctable keys protocol based on the passwords to be iterated. Of course, consideration of specific attacks and the use of known methods of protection against them do not guarantee that the protocol being developed will be persistent, since it is not possible to take into account all existing, but unknown attacks. In this case, methods of mathematical cryptography come to the rescue, which allow to obtain estimates of the strength of protocols in certain security models. Informally speaking, for PAKE protocols, these assessments must strictly prove that testing the password is the best tactic for the adversary when trying to establish a connection, honestly following the protocol. Similar estimates were obtained for the SESPAKE protocol.
As mentioned above, the password is of low entropy value, i.e. unlike the long key, you cannot neglect the probability of just guessing this password. Therefore, paying for the use of passwords as a general pre-agreed secret is the implementation of such technical measures as a limit on the number of attempts to establish a connection.
So, we learned what properties the shared key generation protocol should have based on a password, followed by authentication. We also got acquainted with an example of one of such protocols - the SESPAKE protocol. Let us now try to figure out whether this protocol is really necessary in practice and whether it is impossible to manage with long-existing solutions.
The protocols of this family provide ample opportunities for their use in a wide variety of information systems. In order to "feel" the work of the protocol, let's turn to the most popular area of ​​its application and one of the most important issues for information security - the task of safekeeping of cryptographic keys.
There are two main types of key carriers that use a password: passive storage and active token.
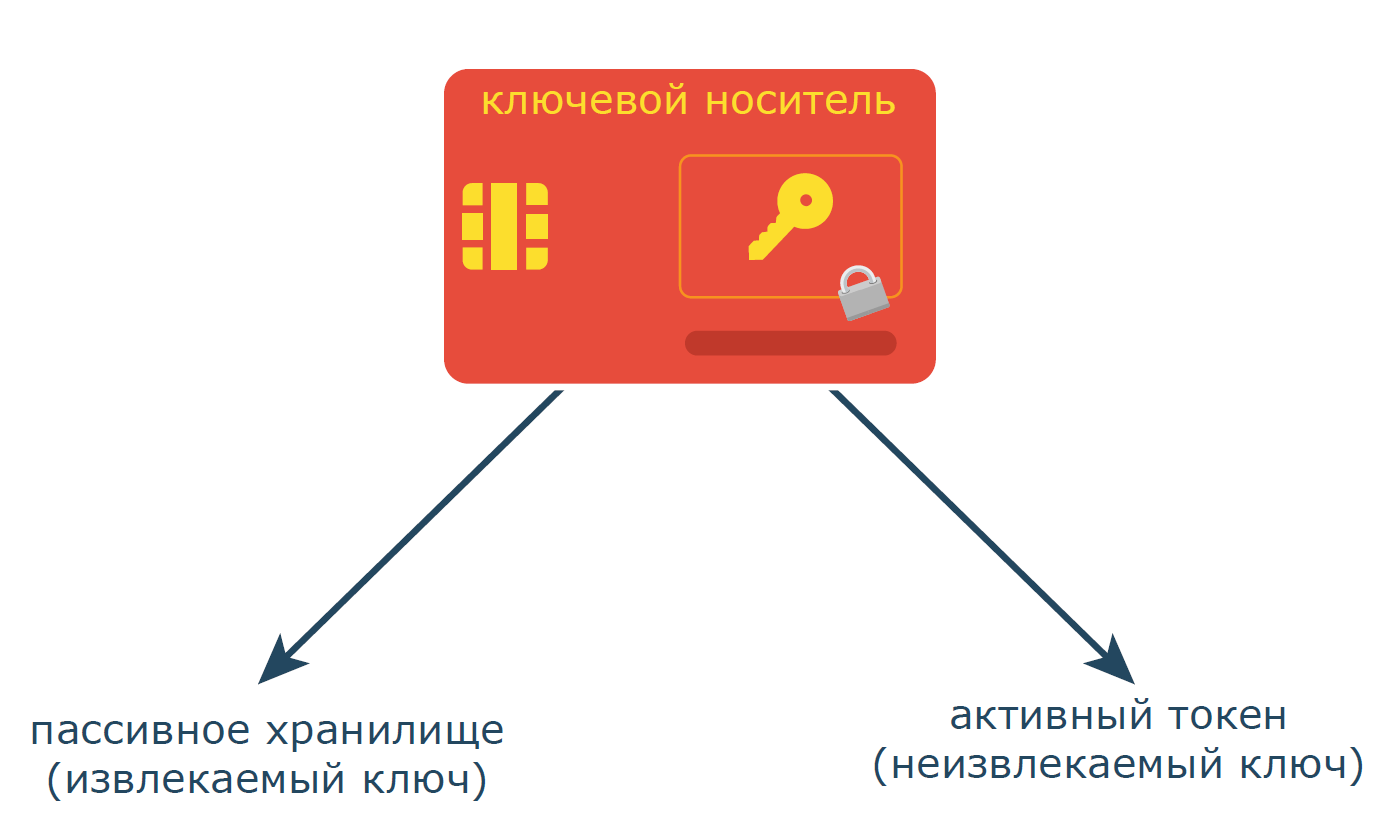
Passive media can only store the key and transfer it to the application (usually the cryptographic provider) running in the operating system on the user's side, which already decides what to do with it. The inherent property of passive storage is the principal retrievability of the key: all operations that depend on the key are performed by the application running on the user's machine, so the key is inevitably present in the RAM. Of course, only the one who knows the password can extract the key.
Active tokens, as well as storage media, also store the user's key within themselves, but the only thing that the user can receive from this carrier is the result of performing cryptographic operations using the stored key. In such devices, the key does not go beyond the memory of the carrier, that is, is non-removable .
The properties of the key carriers of both types described above have rather strict conditions for their use, since both of these key carriers are unstable if the attacker is in the communication channel. In the case of using a storage medium, the attacker simply sees the key, but in the case of the active carrier, he will not be able to access the key, but he will be able to find out the password, and therefore become a legitimate subject for the carrier - who knows the password is right! In this case, if the device is stolen, the attacker can use the token to perform the necessary key operations. In cryptography, such a threat is called selective fake: an attacker can sign the data he needs without knowing the key.
Thus, the problem arises of creating such type of key carriers that would be resistant to the enemy in the communication channel between the machine and the carrier and the threat of selective counterfeiting, that is, would actually solve the authentication problem. And thanks to the advent of the PAKE family of protocols, we can create such a carrier.
This type of tokens that meets these requirements, called functional key carriers (abbreviated as FKN ).
These media, as well as the active media discussed above, provide the user with the opportunity to get only the result of calculations in which the key is involved. However, their difference is that the password is not transmitted directly via the communication channel, but a secure connection is established using the PAKE protocol, that is, only those data are transmitted via the communication channel, which in practice cannot draw any conclusions about the password or information. the key.
This is where the SESPAKE protocol comes on the scene, which, in essence, provides the possibility of such an interaction scenario. Using this protocol allows you to mathematically strictly provide protection against the enemy in the channel. Thus, an attacker who has the ability to read and replace messages in the channel will not be able to find out the password, or even be able to go through passwords non-interactively, that is, without control from the token.
The SESPAKE protocol was developed with all the requirements described above. Usually, the rationale for the strength of the PAKE protocol is given in the model, which takes into account the standard threat of the enemy evoking at least some information about the generated key. However, this model is not entirely natural, as it is considered outside the context of the application of the protocol. Indeed, the keys generated after the completion of the protocol will be further used to protect the data, which will immediately enable the violator to realize the threat. Simply put, the robustness of these protocols is analyzed in some simplified model of their use, which often leads to situations where, after the introduction of extensions that allow using the protocol in specific cases in practice, it turns out to be unstable. Therefore, the justification for the robustness of the SESPAKE protocol is given in the adversary model, which takes into account another stronger threat - the threat of false authentication.
The development of the SESPAKE protocol does not originate from an abstract mathematical model, in which well-known mechanisms of substantiation of persistence exist for a long time, but is associated with a concrete practical case: the need to protect the channel between the key carrier and the provider. Thus, the new model of the adversary introduced by its developers allowed both the protocol and its justification to take into account all the technical aspects important for the practice (for example, work with meters).You can learn more about its rationale in a separate article , but we will try to understand the essence of the protocol’s work.
Of course, the scheme of such a “combat” protocol is significantly more complicated than the examples we are considering, and the protocol itself is based on groups of points of elliptic curves , which, with the same key length, allow us to achieve greater cryptographic strength in comparison with the final fields. However, now even an inexperienced reader will be able to grasp its essence, because the basic principles on which it is based remain the same.
In the above scheme of the protocol's operation, its key and moments already familiar to us, similar to those described in the prototype constructed above, are highlighted in three colors:
The requirement for the presence of different generating elements, formulated by us in conclusion 1, is also not bypassed here. However, now it is formulated as follows: the multiplicity of any point from the set
(a set of points that can be used in the protocol to form a mask, the index ( 
) of which is selected before the start of the key generation stage) relative to the generator 
and relative to each other is unknown. Moreover, the task of calculating this multiplicity is not feasible in practice, i.e. its laboriousness is comparable to the laboriousness of solving a complex discrete logarithm problem in a group of points of an elliptic curve used.
The choice of a point of an elliptic curve, given in the Weierstrass form (
), can be made as follows:
Here
- the order of the field over which the group of points of the elliptic curve is built, and the hash function GOST R 34.11-2012 can be used as, for example.
Note that the SESPAKE protocol is one of the most efficient, since it implies the minimum possible number of shipments between the parties.
At the end of 2015, the technical committee for standardization TK26 adopted a common-key protocol with password-based authentication, the SESPAKE protocol, as guidelines. At about the same time, the protocol began to be considered in the CFRG cryptography research group (Crypto Forum Research Group), which is part of the international standardization organization of the IETF / IRTF. Currently, CFRG is discussing the standardization of requirements for PAKE-type protocols, as well as the choice of protocol as an international recommendation for use. Among the three main candidates is the SESPAKE protocol, draft RFCwhich is now being actively developed by Russian specialists. Acquainted with such protocols, now you can offer your ideas by participating in such discussions.
However, there is a type of protocols that has recently gained increasing popularity, but is still not widely known - shared key generation protocols with password-based authentication. These protocols include the Russian protocol SESPAKE (Security Evaluated Standardized Password Authenticated Key Exchange), with the advent of which in Russia it became necessary to consider the features of protocols of this type. The purpose of this article is rather not to give another formal description of the new protocol, but to help the reader grasp its main idea and features and understand why there are certain steps in it, why they are important, and how this protocol class differs from everything previously known. .
A bit of history
In 1976, Whitfield Diffie and Martin Hellman proposed a simple but ingenious idea of ​​developing a common secret key — the well-known Diffie-Hellman protocol.
Here
')
The durability of this protocol with respect to the passive adversary is based on the so-called CDH problem, which is considered computationally “complex” (if we speak informally, then there are no effective solution algorithms for such a task). The formulation of this problem is as follows: knowing the values
Unfortunately, the Diffie-Hellman protocol has one fundamental flaw: it is not secure if there is an active opponent in the transmission channel (see the “Man in the Middle” attack). The reason for this vulnerability lies in the absence of an authentication mechanism, i.e. during the protocol, the parties are not able to verify in any way that the shared key is developed together with the honest subscriber.
To date, several solutions have been proposed for this problem, here are some of them: the use of certificates and CAs , the introduction of a third trusted participant in the protocol or the use of a previously agreed secret. The latter approach is the simplest solution in terms of implementation. However, if the protocol involves the use of a secret, which is a long bit string, which is difficult for a person to remember, then there is the problem of keeping this secret safe.
The question arises, can we use a short and easily remembered password as a secret ? As soon as the word “password” appears, many people almost reflexively want to say that a priori cannot be achieved a priori, because The password can be quickly recovered by simple brute force or dictionary. It will be shown below that this is not always the case.
To begin with, consider the following key generation scheme, in which an authentication stage is added to the Diffie-Hellman protocol using a secret value:
Here
Why is this example bad in the case when
In this example, the opponent acts as follows: he replaces the side
However, if the use of a password were directly embedded in the generation of a key (which was an inseparable process from its development), the adversary would be able to receive a common
This idea formed the basis of a new approach, namely the common key generation with password-based authentication ( PAKE ).
PAKE protocols
The first protocol of the PAKE type was proposed back in 1992 by Stephen Bellinow and Michael Merritt. This protocol assumed that to solve the authentication problem, subjects wishing to generate a common key use some easy-to-remember password known only to them. The main difference between PAKE protocols and the example considered above is the fact that the password is already used during the generation of the shared key.
In this case, the main requirements for such a protocol are:
- providing authentication for protocol participants;
- the lack of the ability of the enemy to obtain a criterion for brute force
Let us try to understand whether it is difficult to build such a protocol and what features it should have. To do this, consider the simplest example — the prototype of the PAKE protocol:
The blue here highlights the differences from the Diffie-Hellman protocol,
Let's see if such a scheme is vulnerable to an offline dictionary attack. Values ​​are available to the passive adversary listening to the transmission channel
In the case of an active enemy, this scheme still has certain vulnerabilities. Consider the following attack on the scheme, where the discrete logarithms of one generating element relative to another are known. For simplicity, consider the case when
As in the previous attack, here the enemy simply replaces the side
It is easy to see that a similar attack can be carried out even if the protocol uses different generating elements, but the discrete logarithm of one at the base of the other is known. In this case, the value of this logarithm will appear in the chain of equalities simply as some constant.
If we use different generating elements, such that the discrete logarithms of the one relative to the other are not known, we will not be able to get the key as a function only from an unknown password. Really,
Conclusion # 1: When generating an ephemeral public key and a password “mask”, it is necessary to use different generating elements, and the discrete logarithms of one on the basis of the other should be unknown.
To obtain such elements, it is necessary not only to generate them at random, but also to be able to convince everyone else that when they were generated, everything was purely random. This can be achieved if we choose the generating elements according to the principle of provable pseudo-randomness . So, for a multiplicative group of a finite field
- Generate random string
.
- Put
.
- Check that
It would seem that now we have considered all potentially dangerous situations, however, when creating a protocol, it is necessary to take into account more complex issues. Any specialist who develops a new protocol knows that one of the most important requirements for such protocols is to provide them with the so-called implicit authentication of the key generated.
Explicit and implicit key authentication
Implicit key authentication is a protocol property in which a protocol participant can be sure that no other party, except a specially identified (legitimate) protocol participant, can access the secret key generated in the protocol. At the same time, there are no guarantees that the second party to the protocol did indeed gain access to the key, but it is certain that no one else but him could receive it.
Explicit key authentication is a property that is performed when implicit key authentication takes place and the key is confirmed (the property by which one participant of the protocol makes sure that the other participant actually has the key generated in the protocol) at the same time. In this case, it is known that the legitimate side, and no one else, really possesses the key that has been worked out.
Explicit key authentication is a property that is performed when implicit key authentication takes place and the key is confirmed (the property by which one participant of the protocol makes sure that the other participant actually has the key generated in the protocol) at the same time. In this case, it is known that the legitimate side, and no one else, really possesses the key that has been worked out.
For us, this requirement means that the protocol we are designing must provide a cryptographically strong public key that meets the requirement of implicit authentication, even if we use the protocol without an explicit authentication stage. Let us return to our prototype and see if it satisfies this property.
Consider an attack in such an enemy model, where:
- both parties are involved in the interaction;
- the enemy knows the keys
Despite the fact that we use different generating elements, if the enemy knows
You can get rid of this vulnerability by using the hash function in the protocol:
Indeed, since a hash function that satisfies the cryptographic requirements is considered an analog of a pseudo-random function, there are no simple dependencies between its output and input that can be efficiently exploited. Thus, the opponent no longer has the criterion for finding the password and the attack ceases to be applicable.
Conclusion number 2: Hash key generated.
So, we were able to build the simplest prototype of the generation of non-punctable keys protocol based on the passwords to be iterated. Of course, consideration of specific attacks and the use of known methods of protection against them do not guarantee that the protocol being developed will be persistent, since it is not possible to take into account all existing, but unknown attacks. In this case, methods of mathematical cryptography come to the rescue, which allow to obtain estimates of the strength of protocols in certain security models. Informally speaking, for PAKE protocols, these assessments must strictly prove that testing the password is the best tactic for the adversary when trying to establish a connection, honestly following the protocol. Similar estimates were obtained for the SESPAKE protocol.
As mentioned above, the password is of low entropy value, i.e. unlike the long key, you cannot neglect the probability of just guessing this password. Therefore, paying for the use of passwords as a general pre-agreed secret is the implementation of such technical measures as a limit on the number of attempts to establish a connection.
On practice
So, we learned what properties the shared key generation protocol should have based on a password, followed by authentication. We also got acquainted with an example of one of such protocols - the SESPAKE protocol. Let us now try to figure out whether this protocol is really necessary in practice and whether it is impossible to manage with long-existing solutions.
The protocols of this family provide ample opportunities for their use in a wide variety of information systems. In order to "feel" the work of the protocol, let's turn to the most popular area of ​​its application and one of the most important issues for information security - the task of safekeeping of cryptographic keys.
There are two main types of key carriers that use a password: passive storage and active token.
Passive media can only store the key and transfer it to the application (usually the cryptographic provider) running in the operating system on the user's side, which already decides what to do with it. The inherent property of passive storage is the principal retrievability of the key: all operations that depend on the key are performed by the application running on the user's machine, so the key is inevitably present in the RAM. Of course, only the one who knows the password can extract the key.
Active tokens, as well as storage media, also store the user's key within themselves, but the only thing that the user can receive from this carrier is the result of performing cryptographic operations using the stored key. In such devices, the key does not go beyond the memory of the carrier, that is, is non-removable .
Key carrier operation scheme
Storage media:
Active Token:
Active Token:
The properties of the key carriers of both types described above have rather strict conditions for their use, since both of these key carriers are unstable if the attacker is in the communication channel. In the case of using a storage medium, the attacker simply sees the key, but in the case of the active carrier, he will not be able to access the key, but he will be able to find out the password, and therefore become a legitimate subject for the carrier - who knows the password is right! In this case, if the device is stolen, the attacker can use the token to perform the necessary key operations. In cryptography, such a threat is called selective fake: an attacker can sign the data he needs without knowing the key.
CIF or SESPAKE comes into play
Thus, the problem arises of creating such type of key carriers that would be resistant to the enemy in the communication channel between the machine and the carrier and the threat of selective counterfeiting, that is, would actually solve the authentication problem. And thanks to the advent of the PAKE family of protocols, we can create such a carrier.
This type of tokens that meets these requirements, called functional key carriers (abbreviated as FKN ).
The scheme of the functional key carrier (PCF)
The general scheme of their work FKN looks like this:
These media, as well as the active media discussed above, provide the user with the opportunity to get only the result of calculations in which the key is involved. However, their difference is that the password is not transmitted directly via the communication channel, but a secure connection is established using the PAKE protocol, that is, only those data are transmitted via the communication channel, which in practice cannot draw any conclusions about the password or information. the key.
This is where the SESPAKE protocol comes on the scene, which, in essence, provides the possibility of such an interaction scenario. Using this protocol allows you to mathematically strictly provide protection against the enemy in the channel. Thus, an attacker who has the ability to read and replace messages in the channel will not be able to find out the password, or even be able to go through passwords non-interactively, that is, without control from the token.
SESPAKE protocol
The SESPAKE protocol was developed with all the requirements described above. Usually, the rationale for the strength of the PAKE protocol is given in the model, which takes into account the standard threat of the enemy evoking at least some information about the generated key. However, this model is not entirely natural, as it is considered outside the context of the application of the protocol. Indeed, the keys generated after the completion of the protocol will be further used to protect the data, which will immediately enable the violator to realize the threat. Simply put, the robustness of these protocols is analyzed in some simplified model of their use, which often leads to situations where, after the introduction of extensions that allow using the protocol in specific cases in practice, it turns out to be unstable. Therefore, the justification for the robustness of the SESPAKE protocol is given in the adversary model, which takes into account another stronger threat - the threat of false authentication.
The development of the SESPAKE protocol does not originate from an abstract mathematical model, in which well-known mechanisms of substantiation of persistence exist for a long time, but is associated with a concrete practical case: the need to protect the channel between the key carrier and the provider. Thus, the new model of the adversary introduced by its developers allowed both the protocol and its justification to take into account all the technical aspects important for the practice (for example, work with meters).You can learn more about its rationale in a separate article , but we will try to understand the essence of the protocol’s work.
Of course, the scheme of such a “combat” protocol is significantly more complicated than the examples we are considering, and the protocol itself is based on groups of points of elliptic curves , which, with the same key length, allow us to achieve greater cryptographic strength in comparison with the final fields. However, now even an inexperienced reader will be able to grasp its essence, because the basic principles on which it is based remain the same.
In the above scheme of the protocol's operation, its key and moments already familiar to us, similar to those described in the prototype constructed above, are highlighted in three colors:
The requirement for the presence of different generating elements, formulated by us in conclusion 1, is also not bypassed here. However, now it is formulated as follows: the multiplicity of any point from the set
The choice of a point of an elliptic curve, given in the Weierstrass form (
- Generate random string
- Put
.
- If the value is
not a quadratic modulo residue
- Put
.
Here
Note that the SESPAKE protocol is one of the most efficient, since it implies the minimum possible number of shipments between the parties.
Conclusion
At the end of 2015, the technical committee for standardization TK26 adopted a common-key protocol with password-based authentication, the SESPAKE protocol, as guidelines. At about the same time, the protocol began to be considered in the CFRG cryptography research group (Crypto Forum Research Group), which is part of the international standardization organization of the IETF / IRTF. Currently, CFRG is discussing the standardization of requirements for PAKE-type protocols, as well as the choice of protocol as an international recommendation for use. Among the three main candidates is the SESPAKE protocol, draft RFCwhich is now being actively developed by Russian specialists. Acquainted with such protocols, now you can offer your ideas by participating in such discussions.
Source: https://habr.com/ru/post/282043/
All Articles