Can all financial models be erroneous: 7 sources of risk of losses

On Habré and in the analytical section of our site, we write a lot about financial market trends and behavioral strategies on it. Very often, financial models, one way or another, are built on speculative conclusions. And how much the model relies on such data depends on its suitability for use. This indicator can be calculated using the risk model.

The creator of the site Turing Finance and hedge fund analyst NMRQL Stuart Reed published an interesting material on the analysis of the possible risks of using financial models. The material discusses several factors affecting the occurrence of risks - that is, the probability of financial loss when using the model. We present to your attention the main points of this work.
')

False assumptions

At the heart of any financial model are certain assumptions. Therefore, when building a model, it is important to avoid those assumptions that make the model unsuitable for solving the set tasks. Do not forget about the "Occam's razor", do not multiply the essence without need. This rule is especially critical when mastering machine learning. In our case, this principle can be interpreted as follows: if there is a choice between two models with equal accuracy of predictions, one that uses fewer parameters will be more efficient.

This does not mean that “a simple model is better than a complex one”. This is one of the dangerous delusions. The main condition is the equivalence of predictions. It's not about the simplicity of the model. Working with sophisticated computing technologies in finance makes any model indigestible, inelegant, but at the same time more realistic.

There are three types of false premises. No one says that these assumptions, usually taken on faith, make the model absolutely useless. The point is that the risk of its inefficiency exists.

1. Linearity

Linearity is the assumption that the relationship between any two variables can be expressed through a straight line graph. This view is deeply entrenched in financial analysis, since most correlations are linear ratios of two variables.

That is, many were initially convinced that the ratio should be linear, although in reality the correlation may be non-linear. Such models may work for small forecasts, but not cover all their diversity. An alternative is to assume a non-linear behavior. In this case, the model may not cover all the complexity and inconsistency of the described system and suffer from a lack of accuracy.

In other words, if you specify non-linear relationships, any linear measurements will either not be able to identify relationships at all, or will overestimate their stability and durability. What is the problem here?

In portfolio management, the benefits of diversification are based on the use of a matrix of historical correlation for selected assets. If the relationship between any two assets is non-linear (as is the case with some derivatives), the correlation will overestimate or underestimate the benefit. In this scenario, the risks in the portfolio will be less or more than expected. If a company reserves capital for its needs and assumes a linear relationship between various risk factors, this will lead to an error in the amount of capital that must be reserved. Stress tests do not reflect the real risks of companies.

Plus, if a classification is used during model development, where the relationship between two classes of data is non-linear, the algorithm may mistakenly take them as one class of data. A linear classifier can learn how to handle nonlinear data; to do this, use a trick with kernels — a transition from scalar products to arbitrary kernels.

2. Stationarity

The idea of stationarity is that the trader who creates the financial model is convinced that the variable or distribution from which it was isolated is constant over time. In many cases, stationarity is a reasonable assumption. For example, the “heavy” constant is unlikely to change significantly from day to day. That's why it is a constant. But for financial markets, which are adaptive systems, everything is a bit more confusing.

When assessing the risk model should be borne in mind that the correlation, volatility and risk factors may not be stationary. For each of them, the opposite belief leads to its own troubles.

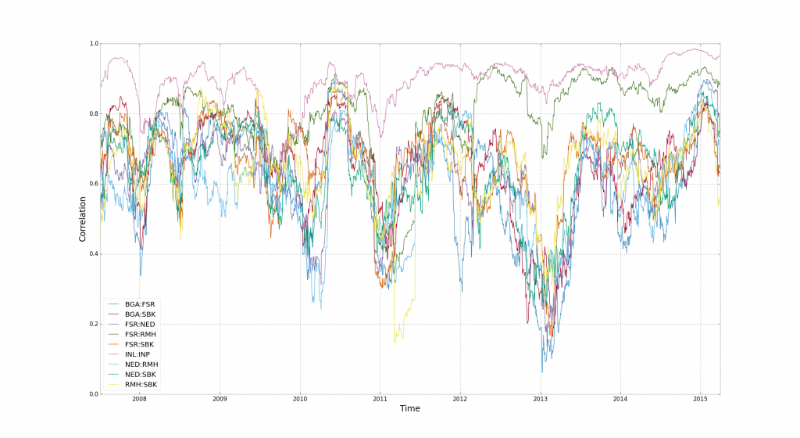
By correlation it was written above. Here, accepting its stationarity distorts the risks of portfolio diversification. Correlations are unstable and “reset” at market reversals.

This chart shows the correlation behavior for 15 financial indices in South Africa. Here time intervals are visible when correlations break. According to Stuart Reed, it’s all a matter of financial leverage and leverage - shares of companies from different industries are “united” by traders who trade them.

Volatility is also most often represented by a stationary variable. Especially if the stochastic approach is used in the equity price model. Volatility is a criterion that determines how much income on securities varies over time. For example, for derivatives, it is believed that the higher the volatility, the higher the prices. Because there is a high probability that derivatives will lose their value. If the model underestimates volatility, most likely there is an underestimation of the value of derivatives.

The stochastic process underlies the Black-Scholes model and works on the principle of the Brownian motion. This model implies constant volatility over time. Feel the difference between the range of possible returns in this model and in the Heston model using the CIR (Cox-Ingerosoll-Ross model) to determine random volatility.

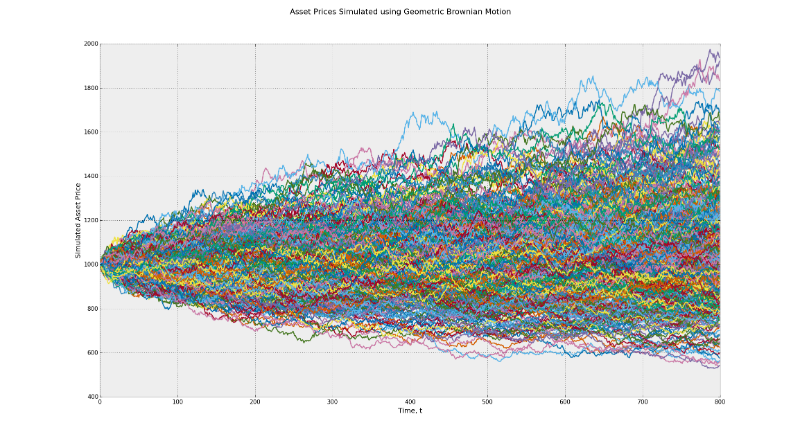
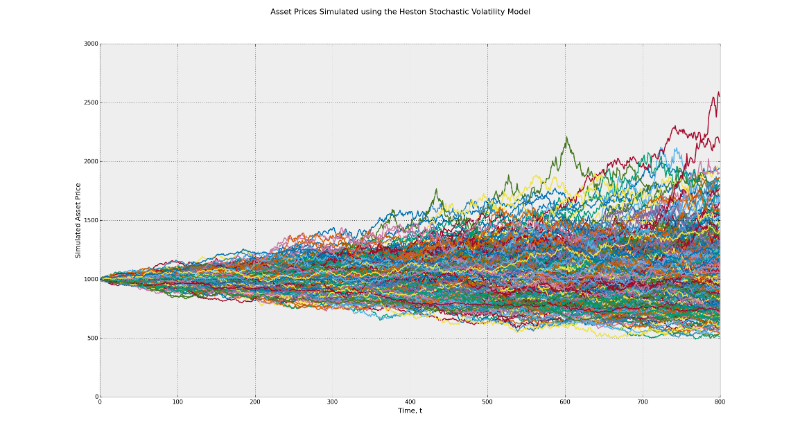
In the first graph, the range of potential end values lies between 500 and 2000. In the second case, it ranges from 500 to 2500. This is an example of the influence of volatility. In addition, many traders, when backing up their strategies by default, take the consideration of the persistence of risk factors. In reality, such factors as momentum, the return of average values can have different effects when the market situation changes seriously.

The gif below shows the dynamic distribution and how the genetic algorithm adapts to changes in distribution over time. Such dynamic algorithms must be used when implementing risk management:

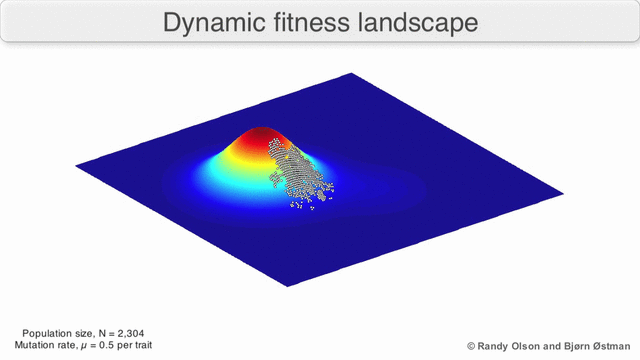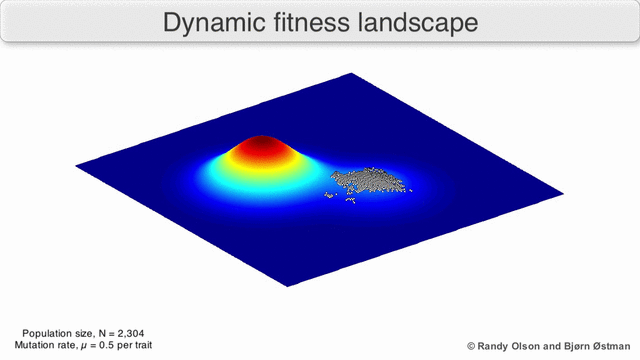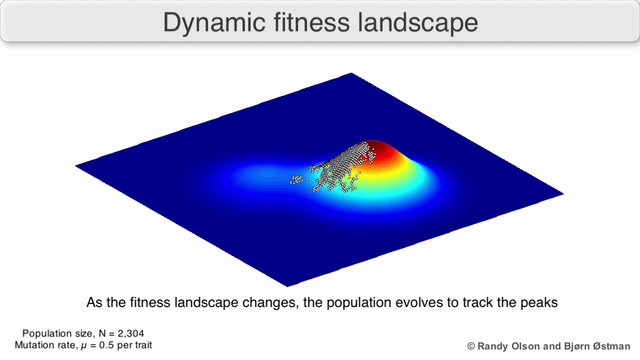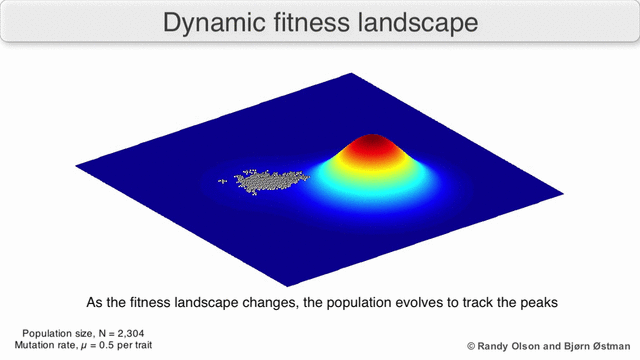
3. Normality

The assumption of normality means that our random variables follow the principle of normal (Gaussian) distribution. This is convenient for several reasons. The combination of any number of normal distributions in the end itself comes to a normal distribution. They are also easily controlled using mathematical formulas, which means that mathematicians are able to create harmonious systems based on it to solve complex problems.

The catch is that many models, including the delta-normal approach, assume that the yield of the market portfolio also has a normal distribution. In the current market yield has its excesses and longer tails. This means that many companies underestimate the impact of tail risk, which they expect (or do not expect) for a market crisis.

An example is the collapse of the market in 1987. On October 19 of that year, most stock markets around the world lost more than 20%. It is noteworthy that in a normal world, where everything follows a normal distribution, this would be impossible.

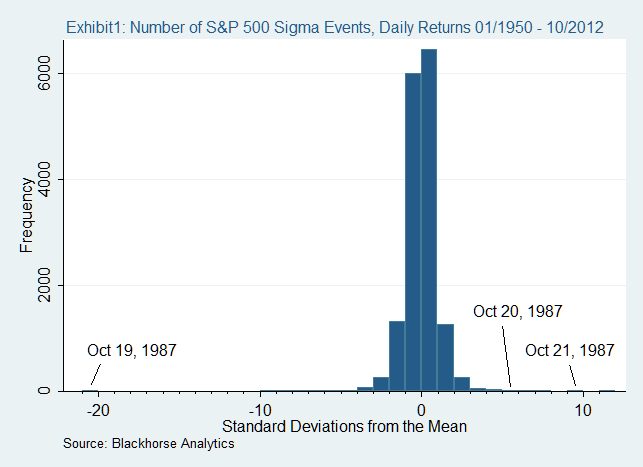
Statistical distortion

Statistics is lying. Unless it satisfies anyone's interests. In the end, it all depends on how it is calculated. The following are the most common causes of distortions in statistics that affect the result.

4. Sampling error

Often, sampling errors lead to a distortion of the statistical result. Simply put, the probability of the pattern presented in the sample depends directly on its probability in the real group. There are several methods for selecting a template. The most popular: random sampling, systematic sampling, stratified and cluster sampling.

In a simple random sample, each pattern has an equal chance of becoming part of the pattern. All this is suitable when the study area contains one class of patterns. Then simple sampling works quickly and efficiently. Another situation arises when you have several classes of patterns, the probability of each is divided into these classes. In this case, the sample will be unrepresentative, and the final result is distorted.

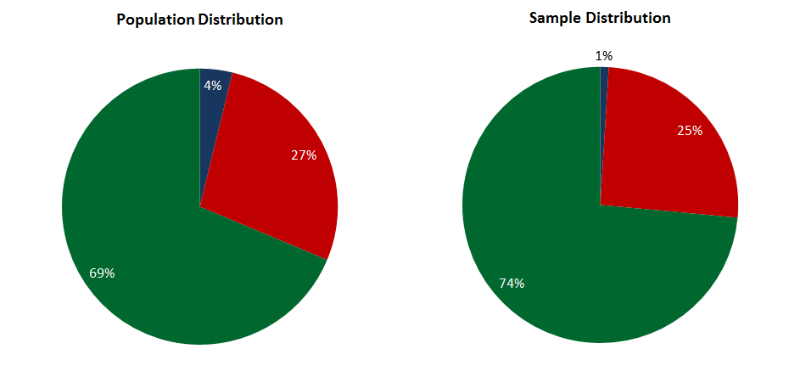
Stratified sampling may be suitable for labeled data, when a certain number of patterns are selected from each class according to its weight. For example, we have specified patterns belonging to three classes - A. B, C. The distribution of patterns over them is 5%, 70% and 25%, respectively. That is, a sample of 100 patterns will contain 5 patterns of class A, 70 - B, and 25 - C. This sample will be representative, but it can be used only for tagged data.

Multistep or cluster sampling allows a stratified approach to unmarked data. At the first stage, data is divided into classes using a cluster algorithm (k-means or ant algorithm). In the second stage, the sample is proportional to the weight and value of each class. Here, the shortcomings of the previous techniques are overcome, but the result begins to depend on the efficiency of the cluster algorithm.

There is also a curse of dimension , which does not depend on the sampling technique used. It means that the number of patterns required for a representative sample increases exponentially along with the attributes in these patterns. At a certain level, it becomes almost impossible to create a representative sample, and thus obtain an undistorted statistic result.

5. Fit errors

The so-called re-fitting happens when a model describes noise (randomness) in a data set, instead of establishing basic statistical relationships. The performance within the sample will be fantastic, outside of the sample - no. Such a model is usually said to have a low level of generalization. Reconfiguration occurs where the model itself is too complicated (or the learning strategy is too simple). The complexity and heaviness in this case are among the parameters that can be configured in the model.

On the quanta forums, you can find many descriptions of how a re-fit occurs. Stuart Reed is confident that quanta intentionally make this mistake in order to show his attitude to the use of complex models by the Luddites. For example, deep neural networks in trading. Some go so far as to state that a simple linear regression will override any complex model. These people do not take into account the effect of under-fit, when the model is too simple to learn the statistical wisdom.

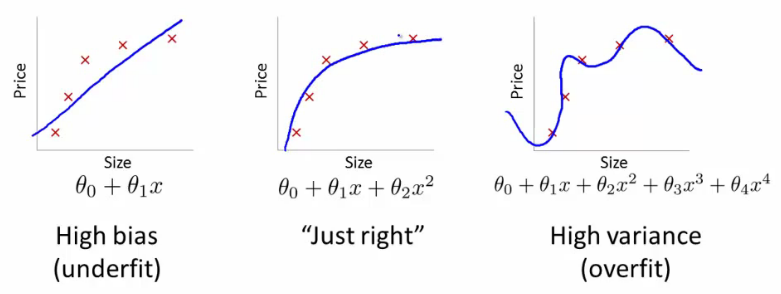
But in any case, no matter how much statistical errors the model may make, much depends on the training strategy. In order to avoid reconfiguration, many researchers use the cross-validation technique. It divides the data set into representative sections: training, testing and validation (confirmation of the result). The data is run through all three sections independently. If a model shows signs of re-fitting, its training is interrupted. The only drawback of this approach: for independent verification, you need a large amount of data.

6. Failure

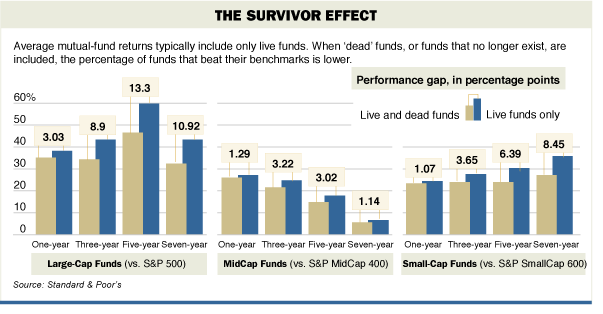
An error will be used for statistical analysis of data that live only on certain periods of time. A classic example of this is the use of hedge fund revenue data. Over the past 30 years, a lot of funds either flew up or collapsed. If we are to operate with data on hedge funds, then take only those that are currently working, says Reed. In this case, we exclude the risks that led to the failure. This indicator is called the survivor effect. How it works is shown in the diagram.

7. Skipping variables

Another error manifests itself when one or more important casual variables are omitted . The model may incorrectly compensate for the missing variable by overestimating the value of other variables. This is especially critical if the included variables are correlated with those that were not included. In the worst case, you get the wrong forecast.

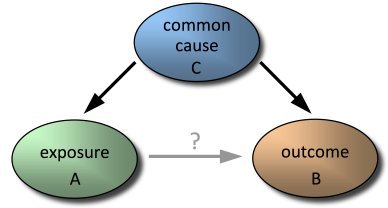
Understanding which independent variables can make a significant contribution to the correctness of the forecast is not easy. The most logical way: to find those variables that would explain most of the deviations in relation to dependent variables. This approach is called best-subset — search for a subset of variables that best predict responses to a dependent variable. An alternative is to find the eigenvectors (a linear combination of the available variables) that are responsible for the deviations in the dependent variables. Typically, this approach is used in conjunction with the principal component method (PCA). The problem with him is that he can re-fit the data. And finally, you can add variables to your model multiple times. This approach is used in multiple linear regression and in adaptive neural networks.

Conclusion

To create a model that would not produce some kind of distortion is almost impossible.
Even if the strategy trader manages to avoid the errors described above, the human factor still remains. Because someone will use the model - even if it is its author himself.

However, the important point here is that despite all the drawbacks and inaccuracies, some models are still useful and work better than others.