Geekly Articles each Day
📜 ⬆️ ⬇️

C # math expression parser - amateur experience

Computer and man - how difficult it is for us to understand each other. In essence, the programming process is an explanation to the machine that you want from it in the language it understands.

As an introduction


In my work, and as a hobby, I am associated with the process of writing code related to mathematical calculations. One of the last tasks was writing software, in which the user would be able to independently enter and use when calculating, visualizing data and optimizing some mathematical expressions. And taking into account his natural laziness and unwillingness to constantly supplement the library of special mathematical functions code, the thought came to mind - why not realize the delusional student idea, and not reinvent the mathematical expression parser's bicycle.

Of course, before taking up the inventive process (again, in view of universal laziness), there was a long enough rape of Yandex and Google for the already existing implementations. And they found, of course, not enough. But unfortunately, what we wanted to achieve from the concrete implementation was not found. And the search criteria were as follows:



The purpose of cycling


Actually, the main objective of the invention of the bicycle was the ability to compile a string of mat.expressions into a delegate with a high speed of the process of calculating the value.
')
Unfortunately, my poor ability to work with search engines, lack of time, effort and laziness did not give a positive result in the search for a prototype and it was decided to embark on a journey on a rake.

Model and main idea


The object model consists of two classes: the parser class and the mathematical expression class. Inside, three additional classes are used: the class of the tree of a mathematical expression, the abstract class of the node of the tree of the mathematical expression, and the class of the logical element of the string of the expression. In addition, the classes of the function, variable, functional and, accordingly, collections of functions, variables and functionals (they are nested in the class of the mathematics expression) are implemented.

The idea that does not pretend to discovery, or the optimal solution, but was an attempt to approach the solution of the problem, was to split the initial sequence of characters in the string of the expression into some logical components. Form a hierarchical sequence of typed logical blocks of mathematical expression. And on its basis to build a tree mat.expressions.

The design started with the idea - “how would I like it to look like it is complete, and what would it be easy and convenient to use?”. I wanted to implement the following usage scenario:

A parser object is created, which is fixed somewhere at the level of the presentation model, or in business logic. It is configured: the necessary constants are added to it, the functions with which it must subsequently work are determined. Event subscribers are added to handle unknown functions and variables. And the parser is waiting for the Parce (string) method call.

In the main Parce () method, a string expression is passed as input, and its result is an object of a mat expression that contains a tree of a mat expression.

The object of the expression must be represented by the collection of functions, variables and constants that are in it. It should be possible to change the values ​​of these objects, as well as the possibility of affecting the expression tree with a view to its modifications. The object of the expression must have a method for calculating the value (by traversing the tree of the expression), receiving as parameters a set of input variables and issuing a numerical value as the result.

The Math object must have a method for converting a Math tree to a System.Linq.Expression object. And a method that allows you to get a compiled delegate right away based on the use of Linq.Expression mechanisms.

Unfortunately, neither the ready-made implementations of something like this, nor the techniques describing, in one way or another, the creation of such a parser are not described anywhere.

Object Model Description


Parser class


Life in the object (after creation) begins with a call to the Parse method.

public MathExpression Parse (string StrExpression)
/// <summary>   </summary> /// <param name="StrExpression">   </param> /// <returns> </returns> [NotNull] public MathExpression Parse([NotNull] string StrExpression) { Contract.Requires(!string.IsNullOrWhiteSpace(StrExpression)); Contract.Ensures(Contract.Result<MathExpression>() != null); StrPreprocessing(ref StrExpression); OnStringPreprocessing(ref StrExpression); var expression = new MathExpression(StrExpression, this); ProcessVariables(expression); ProcessFunctions(expression); return expression; }

Omitting contracts, the meaning of his work comes down to preprocessing a string, calling the constructor of a mat.expression, and post-processing this expression to analyze its variables and functions.

Pre-processing includes two stages:

The private StrPreprocessing method, which removes extra characters from a string:

protected void StrPreprocessing (ref string Str)
 /// <summary>    </summary> /// <param name="Str"> </param> //     ,     protected virtual void StrPreprocessing([NotNull] ref string Str) { Contract.Requires(!string.IsNullOrEmpty(Str)); Contract.Ensures(!string.IsNullOrEmpty(Contract.ValueAtReturn(out Str))); Str = new string(Str.Where(f_ExcludeCharsSet.NotContains).ToArray()); }


and a method for generating a string preprocessing event, so that the user of the parser could independently prepare the string for analysis:

public event EventHandler <EventArgs <string >> StringPreprocessing
 /// <summary>   </summary> public event EventHandler<EventArgs<string>> StringPreprocessing; /// <summary>    </summary> /// <param name="args"> ,   </param> protected virtual void OnStringPreprocessing([NotNull] EventArgs<string> args) { Contract.Requires(args != null); Contract.Requires(args.Argument != null); Contract.Requires(args.Argument != string.Empty); Contract.Ensures(args.Argument != null); Contract.Ensures(args.Argument != string.Empty); StringPreprocessing?.Invoke(this, args); } /// <summary>    </summary> /// <param name="StrExpression"> </param> private void OnStringPreprocessing([NotNull] ref string StrExpression) { Contract.Requires(!string.IsNullOrEmpty(StrExpression)); Contract.Ensures(Contract.ValueAtReturn(out StrExpression) != null); Contract.Ensures(Contract.ValueAtReturn(out StrExpression) != string.Empty); var args = new EventArgs<string>(StrExpression); OnStringPreprocessing(args); StrExpression = args.Argument; }


After the line is cleared of garbage and prepared for parsing, it is passed to the constructor of the matte expression. It also passes the parser itself, which is responsible for determining the functions, constants, and variables.

We will still return to the parser class as its members are mentioned, and now ... Mathematical expression class:

Diagram


The constructor to which the call is passed from the Parse method:

internal MathExpression (string StrExpression, ExpressionParser Parser)
 /// <summary>   </summary> /// <param name="StrExpression">  </param> /// <param name="Parser">  </param> internal MathExpression([NotNull] string StrExpression, [NotNull] ExpressionParser Parser) : this() { Contract.Requires(!string.IsNullOrEmpty(StrExpression)); Contract.Requires(Parser != null); Contract.Ensures(Tree != null); var terms = new BlockTerm(StrExpression); //     var root = terms.GetSubTree(Parser, this); //       f_ExpressionTree = new ExpressionTree(root); //      }


Again, by omitting the block of contracts, first a hierarchical object structure of the terms of a mat expression is created on the basis of a string. Then, from the very first block of it, the method for obtaining the root of the tree of the mat expression is called. And on its basis the constructor of the tree works.

At the first stage of the analysis of the mathematics expression, it is necessary to combine the string representation (sequence of characters) into a sequence of logical blocks. Some of them may be recurrently nested.

Class Hierarchy of Expression Terms


The line is divided into 4 types of terms:


Thus, the entire line is initially represented as one block term, within which the constituent elements lie.

public BlockTerm (string Str)
 /// <summary>   </summary> /// <param name="Str">  </param> public BlockTerm(string Str) : this("", Str, "") { } /// <summary>  </summary> /// <param name="OpenBracket"> </param> /// <param name="Str">  </param> /// <param name="CloseBracket"> </param> public BlockTerm([NotNull] string OpenBracket, [NotNull] string Str, [NotNull] string CloseBracket) : base(string.Format("{0}{2}{1}", OpenBracket ?? "", CloseBracket ?? "", Str)) { Contract.Requires(!string.IsNullOrEmpty(Str)); f_OpenBracket = OpenBracket; f_CloseBracket = CloseBracket; f_Terms = GetTerms(Str); }


Well, the base class of the term:

abstract class Term {...}
 /// <summary>  </summary> abstract class Term { /// <summary> </summary> protected string f_Value; /// <summary>   </summary> /// <param name="Value"> </param> protected Term(string Value) { f_Value = Value; } /// <summary>       </summary> /// <param name="Parser">  </param> /// <param name="Expression"> </param> /// <returns>  .,     </returns> [NotNull] public abstract ExpressionTreeNode GetSubTree([NotNull] ExpressionParser Parser, [NotNull] MathExpression Expression); /// <summary>   .</summary> /// <returns>   .</returns> public override string ToString() => f_Value; }


The breakdown of the substring into its constituent elements is carried out by the GetTerms method:

private static Term [] GetTerms (string Str)
 /// <summary>      </summary> /// <param name="Str">   </param> /// <returns>   </returns> [CanBeNull] private static Term[] GetTerms([CanBeNull] string Str) { if(Str == null) return null; if(Str.Length == 0) return new Term[0]; var pos = 0; var len = Str.Length; var result = new List<Term>(); while(pos < len) { var c = Str[pos]; if(char.IsLetter(c) || c == '∫') { Term value = new StringTerm(GetNameString(Str, ref pos)); if(pos < len) switch(Str[pos]) { case '(': { var blokStr = Str.GetBracketText(ref pos); var block = new BlockTerm("(", blokStr, ")"); value = new FunctionTerm((StringTerm)value, block); } break; case '[': { var blokStr = Str.GetBracketText(ref pos, "[", "]"); var block = new BlockTerm("[", blokStr, "]"); value = new FunctionTerm((StringTerm)value, block); } break; case '{': { var blokStr = Str.GetBracketText(ref pos, "{", "}"); var block = new BlockTerm("{", blokStr, "}"); value = new FunctionTerm((StringTerm)value, block); } break; } if(pos < len && Str[pos] == '{') value = new FunctionalTerm ( (FunctionTerm)value, new BlockTerm("{", Str.GetBracketText(ref pos, "{", "}"), "}") ); result.Add(value); } else if(char.IsDigit(c)) result.Add(new NumberTerm(GetNumberString(Str, ref pos))); else switch(c) { case '(': { var blokStr = Str.GetBracketText(ref pos); var block = new BlockTerm("(", blokStr, ")"); result.Add(block); } break; case '[': { var blokStr = Str.GetBracketText(ref pos, "[", "]"); var block = new BlockTerm("[", blokStr, "]"); result.Add(block); } break; case '{': { var blokStr = Str.GetBracketText(ref pos, "{", "}"); var block = new BlockTerm("{", blokStr, "}"); result.Add(block); } break; default: result.Add(new CharTerm(Str[pos++])); break; } } return result.ToArray(); }


The method starts with checks for the void of the input string and zero length. After that, the current position of the character being analyzed in the string and its length are recorded, after which the symbol at the current position is considered in a loop until reaching the end of the line:

- If it is a letter or an integral symbol, then an attempt is made to capture the name using the GetNameString method.

private static string GetNameString (string Str, ref int pos)
 /// <summary>   </summary> /// <param name="Str"> </param> /// <param name="pos">  </param> /// <returns> </returns> private static string GetNameString([NotNull] string Str, ref int pos) { Contract.Requires(!string.IsNullOrEmpty(Str)); Contract.Ensures(Contract.ValueAtReturn(out pos) >= 0); Contract.Ensures(Contract.ValueAtReturn(out pos) < Str.Length); var result = ""; var L = Str.Length; var i = pos; while(i < L && (char.IsLetter(Str[i]) || Str[i] == '∫')) result += Str[i++]; if(i == L || !char.IsDigit(Str[i])) { pos = i; return result; } while(i < L && char.IsDigit(Str[i])) result += Str[i++]; pos += result.Length; return result; }


After that, the current character is checked for the presence of an opening bracket. If one of the brackets is found, the nested block is extracted from the string, limited by the opening and corresponding closing brackets. The block term created in such a way is placed into the constructor of the functional turma with the indication of the function name set earlier.

A substring delimited by opening and closing parentheses is allocated from a string by an extension method:

public static string GetBracketText (this string Str, ref int Offset, string Open, string Close)
 /// <summary> ///  ,            /// </summary> /// <param name="Str"> </param> /// <param name="Offset"> ///       -         /// </param> /// <param name="Open">  </param> /// <param name="Close">  </param> /// <returns>,       </returns> /// <exception cref="FormatException"> ///      ,        ///       /// </exception> public static string GetBracketText(this string Str, ref int Offset, string Open = "(", string Close = ")") { var Start = Str.IndexOf(Open, Offset, StringComparison.Ordinal); if(Start == -1) return null; var Stop = Str.IndexOf(Close, Start + 1, StringComparison.Ordinal); if(Stop == -1) throw new FormatException(); var start = Start; do { start = Str.IndexOf(Open, start + 1, StringComparison.Ordinal); if(start != -1 && start < Stop) Stop = Str.IndexOf(Close, Stop + 1, StringComparison.Ordinal); } while(start != -1 && start < Stop); if(Stop == -1 || Stop < Start) throw new FormatException(); Offset = Stop + Close.Length; Start += Open.Length; return Str.Substring(Start, Stop - Start); }


First, the indices of the first occurrences of the beginning and end characters are determined. If the initial character is not found, then return void. If not found the final character, then this is a format error.

The idea of ​​the method in the sequential cyclic search patterns start and end of the line. We are trying to find the next opening symbol. If it is found, and it stands before the closing one, then the index of the closing character must be updated. The cycle continues until there is such a closing character that is not preceded by the opening character.

The result of the method is a substring between the opening and closing characters.

If after the formed functional torm there is an opening brace, then the body of the functional begins. Select the contents of the curly brackets in the block and create a term-functional, pointing to it a term-function, which in this context will contain the name of the functional and its parameters, and the body will be a block in curly brackets.

If no brackets were found, the name found is a literal (the future variable ... or a constant).

- If the next character of the string was a digit, then an integer begins. Select the substring containing only numbers.

private static string GetNumberString (string Str, ref int pos)
 /// <summary>  </summary> /// <param name="Str"> </param> /// <param name="pos">   </param> /// <returns>  </returns> private static string GetNumberString([NotNull] string Str, ref int pos) { Contract.Requires(!string.IsNullOrEmpty(Str)); Contract.Ensures(Contract.ValueAtReturn(out pos) >= 0); Contract.Ensures(Contract.ValueAtReturn(out pos) < Str.Length); var p = pos; var l = Str.Length; while(p < l && !char.IsDigit(Str, p)) p++; if(p >= l) return null; var start = p; while(p < l && char.IsDigit(Str, p)) p++; pos = p; return Str.Substring(start, p - start); }


The result of this method - a string with numbers - falls into the constructor of an integer jerk.

- If the next character in the string is an opening bracket, then the block begins. Select its substring with the GetBracketText extension method.
- If the next character is not a bracket, then it is an indefinite character that turns into a character torm.

All created terms are first collected from the list, and then returned as an array.

Constructors of all other terms are less interesting. They simply store the resulting parameters in internal fields (possibly with type conversion).

After that, the string will be transformed into a logical hierarchical structure of nested sequences of terms of different types. From this sequence, a binary tree of a mat expression is built recursively.

The basis of the tree is the base class of the node of the tree mat.

Class hierarchy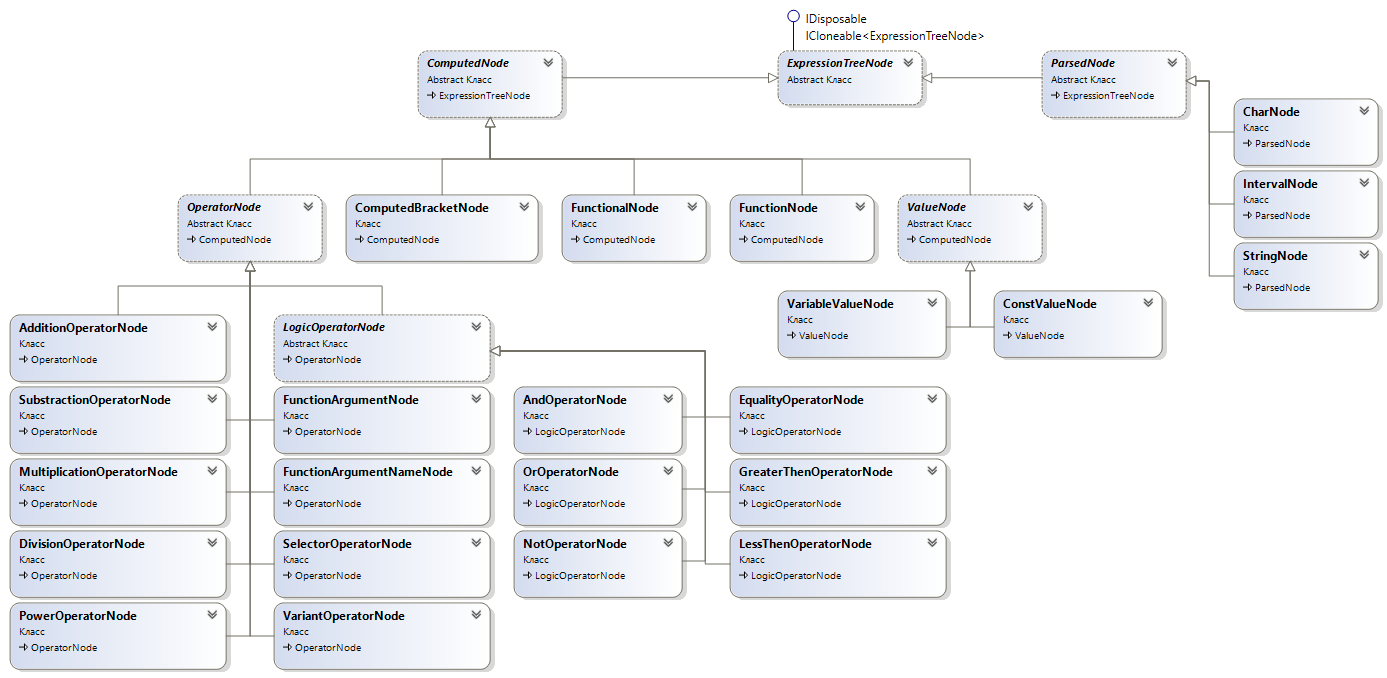


Each node is a class that stores references to the node-root of the left subtree and the node-root of the right subtree, as well as a link to its ancestor. The abstract tree node class provides an interface for accessing ancestor / descendant nodes, traversal methods, functional indexers that allow to get enumerations of nodes associated with the current, recursive methods for obtaining variables, functions, etc., as the root of its subtree. The base class of the node also provides a number of computable properties: attributes - whether the node is a left / right subtree, whether the node is a root, a link to the root of the tree, a symbolic path to the current node from the root of the tree, and an ancestor iterator.

Tree node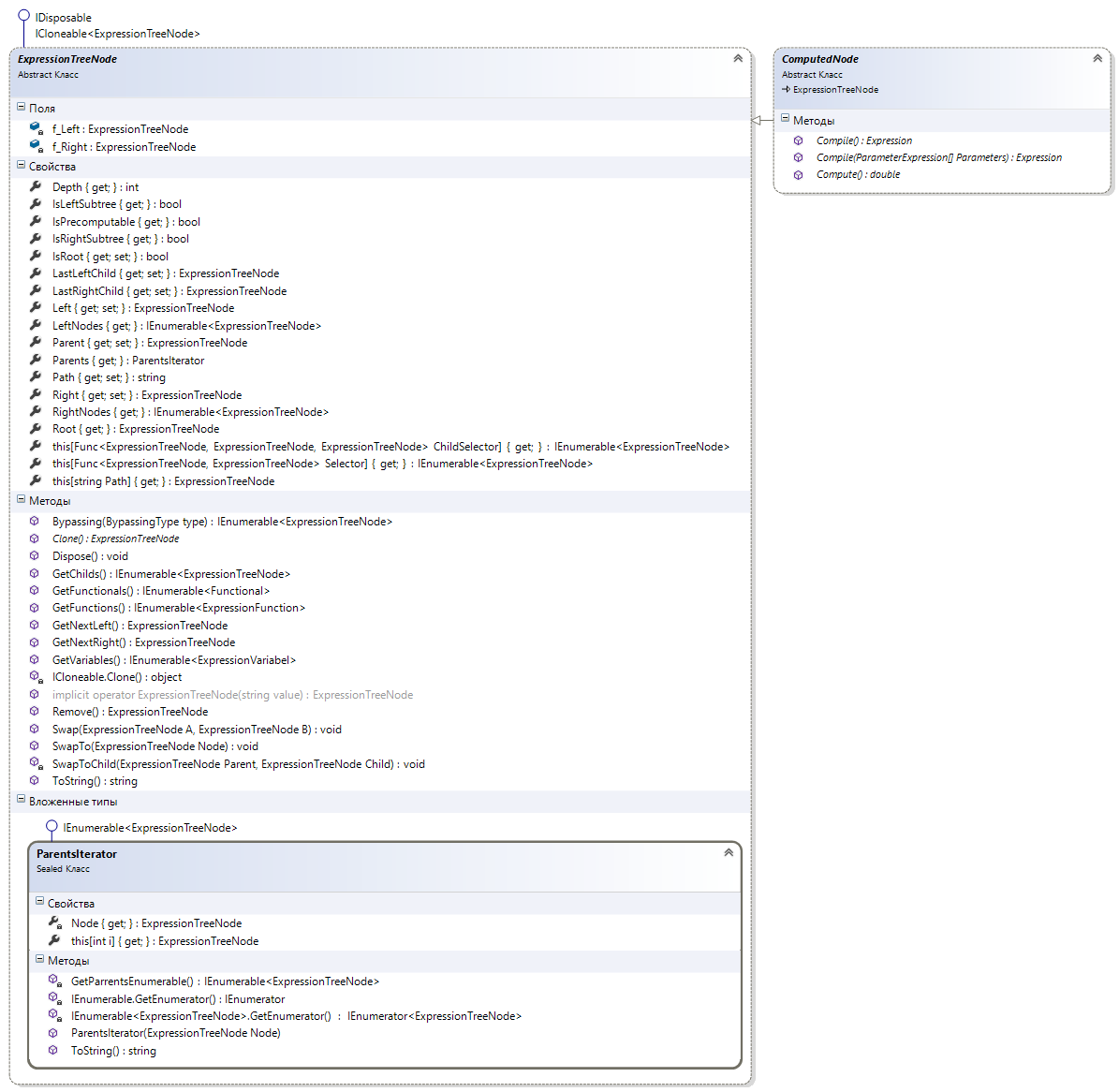


The code of this class allows you to perform basic manipulations with elements of the tree for their replacement, permutation, traversal and access. I will give separate methods as required. Full text takes up a lot of space. It can be viewed / copied from project sources.

All tree nodes can be either computable or used in parsing.

The parse nodes include a string node, a character node, and an interval value node. They are needed to supplement certain metostructures in the tree, such as the integration functional, where the interval must be specified.

Computable nodes are essential in the resulting tree structure. They represent all the elements that can be described in the expression.

These include:


Tree building process


The term class declares the abstract method GetSubTree, which allows you to get a subtree described by it from any term. The process of building a tree begins with calling this method on the block term formed from the source line.

public override ExpressionTreeNode GetSubTree (ExpressionParser Parser, MathExpression Expression)
 /// <summary>   </summary> /// <param name="Parser"> </param> /// <param name="Expression"> </param> /// <returns> </returns> public override ExpressionTreeNode GetSubTree(ExpressionParser Parser, MathExpression Expression) { Contract.Requires(Parser != null); Contract.Requires(Expression != null); Contract.Ensures(Contract.Result<ExpressionTreeNode>() != null); var separator = Parser.ExpressionSeparator; //  -  //      ,  - //             var roots = Terms .Split(t => t is CharTerm && ((CharTerm)t).Value == separator) .Select(g => Parser.GetRoot(g, Expression)).ToArray(); if(roots.Length == 1) return roots[0]; //     ,    //     ExpressionTreeNode argument = null; //     for(var i = 0; i < roots.Length; i++) //      { var root = roots[i]; ExpressionTreeNode arg; //     if(root is FunctionArgumentNode) // -   arg = root; // --     else if(root is FunctionArgumentNameNode) // -    // --      arg = new FunctionArgumentNode(root as FunctionArgumentNameNode); else if(root is VariantOperatorNode && root.Left is VariableValueNode) arg = new FunctionArgumentNode(((VariableValueNode)root.Left).Name, root.Right); else // -     arg = new FunctionArgumentNode("", root); // --      if(argument == null) argument = arg; //     ,    ,   else //  argument = argument.Right = arg; //        } //     ,  -    -   if(argument == null) throw new FormatException("   "); return argument.Root; //    }


The method extracts a symbol from the object of the expression mat that is passed to it, which separates the expressions in the block. The default delimiter is ';' - semicolon.

Then, in the Linq-sequence, the entire array of nested terms is divided into subarrays by a separator - a symbolic term containing an expression separator character. The Split extension method is responsible for this.

public static T [] [] Split <T> (this T [] array, Func <T, bool> Splitter)
 /// <summary>      </summary> /// <typeparam name="T">  </typeparam> /// <param name="array"> </param> /// <param name="Splitter">,  ,     </param> /// <returns> ///     ,     . ///      . /// </returns> [NotNull] public static T[][] Split<T>([NotNull] this T[] array, [NotNull] Func<T, bool> Splitter) { Contract.Requires(array != null); Contract.Requires(Splitter != null); Contract.Ensures(Contract.Result<T[][]>() != null); var result = new List<T[]>(array.Length); var aggregator = new List<T>(array.Length); for(var i = 0; i < array.Length; i++) { var value = array[i]; if(Splitter(value) && aggregator.Count != 0) { result.Add(aggregator.ToArray()); aggregator.Clear(); } else aggregator.Add(value); } if(aggregator.Count != 0) result.Add(aggregator.ToArray()); return result.ToArray(); }


For each of the subarray of terms, the GetRoot parser method is called, which is designed to determine the root of the tree of this group of terms. Then all found roots are combined into an array.

GetRoot method:

internal ExpressionTreeNode GetRoot (Term [] Group, MathExpression MathExpression)
 /// <summary>        </summary> /// <param name="Group">   </param> /// <param name="MathExpression">   </param> /// <returns>  .</returns> internal ExpressionTreeNode GetRoot([NotNull] Term[] Group, [NotNull] MathExpression MathExpression) { Contract.Requires(Group != null); Contract.Requires(MathExpression != null); Contract.Ensures(Contract.Result<ExpressionTreeNode>() != null); //       ExpressionTreeNode Last = null; for(var i = 0; i < Group.Length; i++) //       { var node = Group[i].GetSubTree(this, MathExpression); //       //    ... if(Group[i] is NumberTerm) // ...  ,  { //...                if(i + 2 < Group.Length && NumberTerm.TryAddFractionPart(ref node, Group[i + 1], DecimalSeparator, Group[i + 2])) i += 2; //...      . } else if(Group[i] is BlockTerm) //...   ( ) node = new ComputedBracketNode( //    -    new Bracket( // : (((BlockTerm)Group[i]).OpenBracket), //     ((BlockTerm)Group[i]).CloseBracket), //     node); //   //       Combine(Last, Last = node); //       if(Last.IsRoot && Last is VariantOperatorNode && Last.Left is VariableValueNode) Last = new FunctionArgumentNameNode(((VariableValueNode)Last.Left).Name); OnNewNodeAdded(ref Last); } //      ,     if(Last == null) throw new FormatException(); return Last.Root; //      }


. ( ). :

— , .

public static bool TryAddFractionPart(ref ExpressionTreeNode node, Term SeparatorTerm, char DecimalSeparator, Term FrationPartTerm)
 /// <summary>    </summary> /// <param name="node"> </param> /// <param name="SeparatorTerm"> </param> /// <param name="DecimalSeparator">    </param> /// <param name="FrationPartTerm">    </param> /// <returns>,    . ,        </returns> public static bool TryAddFractionPart(ref ExpressionTreeNode node, Term SeparatorTerm, char DecimalSeparator, Term FrationPartTerm) { var value = node as ConstValueNode; if(value == null) throw new ArgumentException("   "); var separator = SeparatorTerm as CharTerm; if(separator == null || separator.Value != DecimalSeparator) return false; var fraction = FrationPartTerm as NumberTerm; if(fraction == null) return false; var v_value = fraction.Value; if(v_value == 0) return true; node = new ConstValueNode(value.Value + v_value / Math.Pow(10, Math.Truncate(Math.Log10(v_value)) + 1)); return true; }


The method specifies the separator character of the integer and fractional part of the decimal number, as well as the two following terms. If the second term is a symbolic one and contains a separator character, and the third is a numeric one, then the node is replaced with a new node-constant value
— the Second check — if the current term is block, then the node-block-box is formed.

Upon completion of checks, the method combining the node created on the previous cycle with the current one is executed:

public virtual void Combine (ExpressionTreeNode Last, ExpressionTreeNode Node)
 /// <summary>     </summary> /// <param name="Last">   (   )</param> /// <param name="Node"> ,     </param> // ReSharper disable once CyclomaticComplexity public virtual void Combine([CanBeNull] ExpressionTreeNode Last, [NotNull] ExpressionTreeNode Node) { Contract.Requires(Node != null); if(Last == null) return; //      ,  if(Node is CharNode) //    -  ,  { Last.LastRightChild = Node; //       return; } var operator_node = Node as OperatorNode; //      - if(operator_node != null) //     ... { //    : //         //            var parent_operator = Last as OperatorNode ?? Last.Parent as OperatorNode; if(parent_operator != null) //      - (   )...  { //           -   // op <-     // | // op // / \ // null ? if(parent_operator.Left == null && parent_operator.Parent is OperatorNode) parent_operator = (OperatorNode)parent_operator.Parent; if(parent_operator.Left == null) //      ... operator_node.Left = parent_operator; //         else if(parent_operator.Right == null) //      parent_operator.Right = Node; //       else //     { var priority = operator_node.Priority; //     //     ,     if(priority <= parent_operator.Priority) { //          parent_operator = (OperatorNode)parent_operator.Parents //            .TakeWhile(n => n is OperatorNode && priority <= ((OperatorNode)n).Priority) //     .LastOrDefault() ?? parent_operator; //    ,     //            if(parent_operator.IsRoot) //    -   //       ,      if(priority <= parent_operator.Priority) //       operator_node.Left = parent_operator; else //       { var parent = parent_operator.Parent; //       parent.Right = Node; //        operator_node.Left = parent_operator;//       } } else //       { //          parent_operator = (OperatorNode)parent_operator.RightNodes //              .TakeWhile(n => n is OperatorNode && n.Left != null && ((OperatorNode)n).Priority < priority) //     .LastOrDefault() ?? parent_operator; //    ,     //            var right = parent_operator.Right; //      parent_operator.Right = Node; //        operator_node.Left = right; //         } } } else //       { var parent = Last.Parent; var is_left = Last.IsLeftSubtree; var is_right = Last.IsRightSubtree; operator_node.Left = Last; //       if(is_left) parent.Left = operator_node; else if(is_right) parent.Right = operator_node; } return; //  } //       if(Last is OperatorNode) //      { Last.Right = Node; //       return; //  } //          //    ,        -  if(Last is ConstValueNode || (Last is ComputedBracketNode && Node is ComputedBracketNode)) { //      var parent = Last.Parent; if(parent != null) //    //            parent.Right = new MultiplicationOperatorNode(Last, Node); else //       //   -     ,      new MultiplicationOperatorNode(Last, Node); return; // . } Last.Right = Node; }


. , ., , - ( ). , . .

: — , - <>:<_2>, <_>:<_>. .

- NewNodeAdded, . , .

, GetSubTree , :



:


.

. . :

class StringTerm : Term {...}
 /// <summary>  </summary> class StringTerm : Term { /// <summary>  </summary> [NotNull] public string Name => f_Value; /// <summary>  </summary> /// <param name="Name">  </param> public StringTerm([NotNull] string Name) : base(Name) { Contract.Requires(!string.IsNullOrEmpty(Name)); } /// <summary> ,   -</summary> /// <param name="Parser"></param> /// <param name="Expression"> </param> /// <returns>   ,   Expression.Variable[Name]</returns> public override ExpressionTreeNode GetSubTree(ExpressionParser Parser, MathExpression Expression) => new VariableValueNode(Expression.Variable[Name]); } /// <summary>  </summary> sealed class FunctionalTerm : FunctionTerm { /// <summary> </summary> [NotNull] public BlockTerm Parameters { get; set; } /// <summary>   </summary> /// <param name="Header"> </param> /// <param name="Body"> </param> public FunctionalTerm([NotNull] FunctionTerm Header, [NotNull] BlockTerm Body) : base(Header.Name, Body) { Contract.Requires(Header != null); Contract.Requires(Body != null); Parameters = Header.Block; } /// <summary>   </summary> /// <param name="Parser"></param> /// <param name="Expression"> </param> /// <returns>  </returns> public override ExpressionTreeNode GetSubTree(ExpressionParser Parser, MathExpression Expression) => new FunctionalNode(this, Parser, Expression); public override string ToString() => $"{Name}{Parameters}{Block}"; }


, / -/.

internal FunctionNode(FunctionTerm Term, ExpressionParser Parser, MathExpression Expression)
 /// <summary>   </summary> /// <param name="Term"> </param> /// <param name="Parser"> </param> /// <param name="Expression"> </param> internal FunctionNode(FunctionTerm Term, ExpressionParser Parser, MathExpression Expression) : this(Term.Name) { var arg = Term.Block.GetSubTree(Parser, Expression); if(!(arg is FunctionArgumentNode)) if(arg is FunctionArgumentNameNode) arg = new FunctionArgumentNode((FunctionArgumentNameNode)arg); else if(arg is VariableValueNode) arg = new FunctionArgumentNode(null, arg); else if(arg is VariantOperatorNode && arg.Left is VariableValueNode) arg = new FunctionArgumentNode(((VariableValueNode)arg.Left).Name, arg.Right); else arg = new FunctionArgumentNode(null, arg); Right = arg; // -   Function = Expression.Functions[Name, ArgumentsNames]; }


. . . , ( , - .


«» . . Parse ProcessVariables ProcessFunctions «» .

:

internal void ProcessVariables(MathExpression Expression)
 /// <summary> </summary> /// <param name="Expression">  </param> internal void ProcessVariables([NotNull] MathExpression Expression) { Contract.Requires(Expression != null); var tree_vars = Expression.Tree.Root.GetVariables().ToArray(); Expression.Variable .Where(v => !tree_vars.Contains(v)) .ToArray() .Foreach(v => Expression.Variable.Remove(v)); foreach(var variable in Expression.Variable.ToArray()) { if(f_Constans.ContainsKey(variable.Name)) { Expression.Variable.MoveToConstCollection(variable); variable.Value = f_Constans[variable.Name]; } OnVariableProcessing(variable); } }


Its task is to bypass the tree, find all the variable nodes and extract the variable objects used in them. After that, it is necessary to remove everything that is not used in the tree from the collection of variables of the mathematics expression.

After that, for each variable in the tree it is checked whether its name is in the collection of known parser constants. If yes, then it is removed from the collection of variables of the expression, entered into the collection of constants of the expression, initialized to the value known to the parser, and the flag is set in it that it is a constant.

After that, a new variable detection event is called for it in the parser. When processing this event, the user of the parser can override the value of this variable, or change the object of the variable itself.

The second Method ProcessFunctions method fills in functions known to the expression expression:

internal void ProcessFunctions (MathExpression Expression)
 /// <summary> </summary> /// <param name="Expression">  </param> [SuppressMessage("ReSharper", "CyclomaticComplexity")] internal void ProcessFunctions([NotNull] MathExpression Expression) { Contract.Requires(Expression != null); foreach(var function in Expression.Functions) switch(function.Name) { case "Sin": case "SIN": case "sin": if(function.Arguments.Length != 1) goto default; function.Delegate = new Func<double, double>(Math.Sin); break; case "COS": case "Cos": case "cos": if(function.Arguments.Length != 1) goto default; function.Delegate = new Func<double, double>(Math.Cos); break; case "TAN": case "Tan": case "tan": case "tn": if(function.Arguments.Length != 1) goto default; function.Delegate = new Func<double, double>(Math.Tan); break; case "ATAN": case "ATan": case "Atan": case "atan": case "atn": case "Atn": if(function.Arguments.Length == 1) function.Delegate = new Func<double, double>(Math.Atan); else if(function.Arguments.Length == 2) function.Delegate = new Func<double, double, double>(Math.Atan2); else goto default; break; case "Atan2": case "atan2": if(function.Arguments.Length != 2) goto default; function.Delegate = new Func<double, double, double>(Math.Atan2); break; case "CTG": case "Ctg": case "ctg": if(function.Arguments.Length != 1) goto default; function.Delegate = new Func<double, double>(x => 1 / Math.Tan(x)); break; case "Sign": case "sign": if(function.Arguments.Length != 1) goto default; function.Delegate = new Func<double, double>(x => Math.Sign(x)); break; case "Abs": case "abs": if(function.Arguments.Length != 1) goto default; function.Delegate = new Func<double, double>(Math.Abs); break; case "Exp": case "EXP": case "exp": if(function.Arguments.Length != 1) goto default; function.Delegate = new Func<double, double>(Math.Exp); break; case "Sqrt": case "SQRT": case "√": case "sqrt": if(function.Arguments.Length != 1) goto default; function.Delegate = new Func<double, double>(Math.Sqrt); break; case "log10": case "Log10": case "LOG10": case "lg": case "Lg": case "LG": if(function.Arguments.Length != 1) goto default; function.Delegate = new Func<double, double>(Math.Log10); break; case "loge": case "Loge": case "LOGe": case "ln": case "Ln": case "LN": if(function.Arguments.Length != 1) goto default; function.Delegate = new Func<double, double>(Math.Log); break; case "log": case "Log": case "LOG": if(function.Arguments.Length != 2) goto default; function.Delegate = new Func<double, double, double>(Math.Log); break; default: var f = OnFunctionFind(function.Name, function.Arguments); if(f == null) throw new NotSupportedException($"  {function.Name}  "); function.Delegate = f; break; } }


If the function name is among the variants of the case statement, then if the required function matches the number of arguments, it is assigned a delegate who will calculate its value. If the function is not defined, the delegate is defined as the result of generating an unknown function detection event. In this case, the user can determine in the response to this event the desired delegate by the name and the number (and names) of the arguments.

This completes the generation of mathematical expressions.

Using


Suppose we have a task to calculate the integral of the function A * cos (2 * x) / pi + G (x / 2) divided by A and + 1, where G (x) = 2cos (x). When A, say, equal to 5. And the integral must be taken in increments of 0.05.

 var parser = new ExpressionParser(); parser .FindFunction += (s, e) => { if(e.SignatureEqual(name: "G", ArgumentsCount: 1)) e.Function = new Func<double, double>(x => 2 * Math.Cos(x)); }; var expr = parser.Parse(@"Int[x=-10..10;dx=0.05]{A*cos(2x) + G(x/2)}/A + 1"); expr.Variable["A"] = 5; var y = expr.Compute(); //y = 0.30928806858920344 var f = expr.Compile(); var y2 = f(); //y = 0.30928806858920344

Conclusion


Given the resulting volume of the article, I put here ... not a full point, but a semicolon. As a result of the above, it was possible:

  1. Get a general idea of ​​the method of solving the problem;
  2. To form an object model of the parser of the mat expression, the mat expression itself and its tree;
  3. To create an effective method for parsing the string of mathematical expressions into logical components;
  4. Create an effective method for constructing a tree of mathematical expressions, taking into account the peculiarities of using brackets, operator priorities and special constructions (functionals);
  5. Provide control over different stages of input data processing by the parser based on the event system;
  6. Add the ability to expand functionality.

What could not be described in this article:

  1. The logic of the variables (their types and methods for their production and subsequent replacement);
  2. The structure of collections of variables, constants, functions involved in the work of mathematical expression;
  3. The method of calculating the value of a mat expression by traversing its tree;
  4. The method of compiling the tree of mathematics in the delegate.

What has not been possible so far in the implementation of the parser itself:

  1. Implement methods for optimizing the tree of mat expression;
  2. Remove crutches from a number of places;
  3. Add checks for compliance of the input data with the format of the matte expression;
  4. Actually, outline the boundaries of this format;
  5. Increase code coverage with unit tests;
  6. To conduct comparative studies of the speed of both the parsing stages and the computation steps.

In general, the work on this code unfortunately is of a background character and has been going on for a couple of years already, but at this stage it is already solving the tasks assigned to it. Although in the present form it is impossible to let it go in production.

Full source codes can be found here .

Source: https://habr.com/ru/post/281495/

More articles:


All Articles