Character regression and another approach

Symbolic regression is considered very interesting. "Find me a function that is best suited to solve the problem." And on Habré, I have already met a post in which the author considered one of the evolutionary algorithms as applied to this problem ( here it is ).

Genetic programming is indeed a powerful method. But in this article I want to consider another (no less interesting) method - grammatical evolution. I will not talk about him for a long time. Let me just say that the method uses a free grammar in the form of Backus-Naur, as well as any evolutionary algorithm as a “engine” (I chose the genetic algorithm). And the method is very cool!

I will go straight to the example. As a workhorse, I chose the Duffing Oscillator .

I will describe the task. There is a second order nonhomogeneous differential equation:

$\ dot {x} \ dot {} + \ delta \ dot {x} - \ beta x + \ alpha x ^ 3 = F \ cos (\ omega t)$

Make it homogeneous (unforced OD):

$\ dot {x} \ dot {} + \ delta \ dot {x} - \ beta x + \ alpha x ^ 3 = 0$

After reducing the equation to the Cauchy normal form, we obtain the following system:

$\ dot {x} = y \\ \ dot {y} = \ beta x - \ alpha x ^ 3 - \ delta y$

Let be $\ beta = 1, \ alpha = 1, \ delta = 0$ and the initial conditions vector $X_0 = [x_1, x_2] ^ T$

The vector of initial conditions will be equal to [1,1]. Objective: to obtain such a function u (t, x), which in the shortest time will transfer the system from the state [1,1] to [0,0].

Diffur system code:

Duffing = [ lambda t,x: x[1], lambda t,x: -x[0] - x[0]**3 + u(t,x) ]

It remains to consider the grammar that I chose for the method:

 grammar = { '<expr>' : [ '(<expr>)<op>(<expr>)', '<val>', '<func1>(<expr>)' ], '<op>' : [ '+', '-', '*', '/' ], '<val>' : [ 'x2', 'x1', '(smallConst)', '(bigConst)' ], "<func1>": [ 'minus','math.sin', ] }

It is primitive, but gives the desired result. I note that smallConst is a constant in the interval [0,1], and bigConst is a constant in the interval [0,200].

Run the genetic algorithm with parameters

The length of the chromosome (each number in the chromosome is an integer value in the range from 0 to 200) = 10
Population length = 50.
The number of iterations (duration of evolution) = 200.

We get the following result:

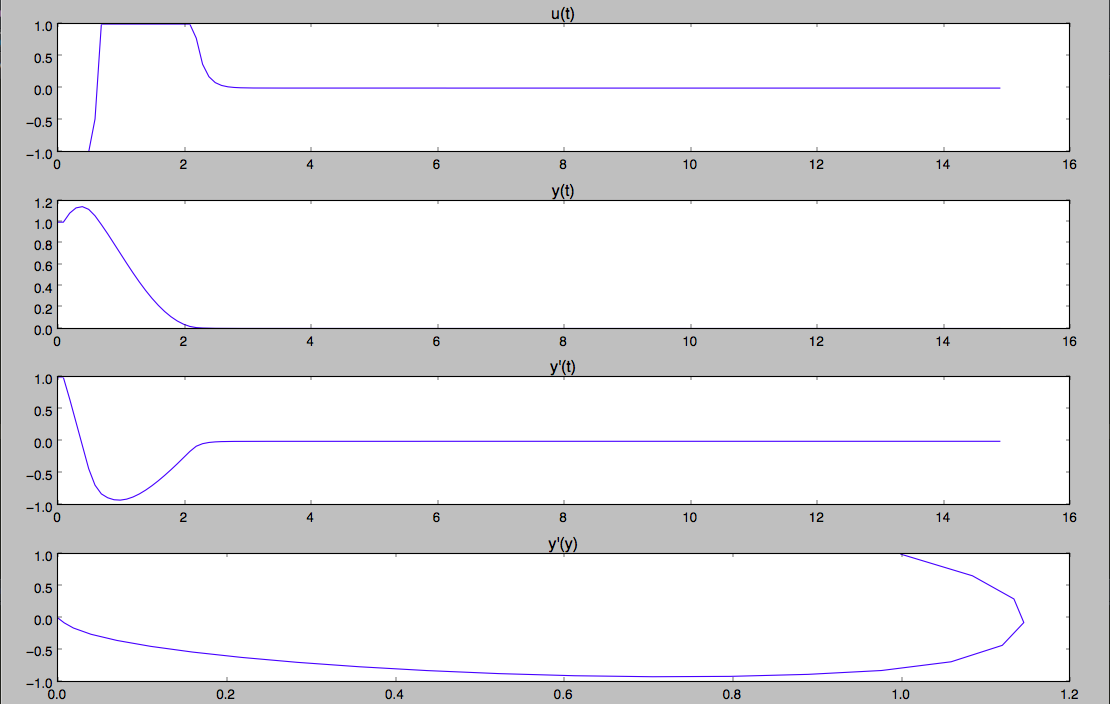
2.5 seconds - the transition time.

u (t, x) = ((minus (x2)) - ((x1) ((0.69028)))) ((11)) (quite understandable, although many brackets)

To obtain the average time of the transition process, you need to run the algorithm more than once (this is obvious). But in this article I wanted to show that the algorithm works (!!) and gives the result.

Conclusion: Grammatical evolution is a young but powerful tool in solving problems of symbolic regression. Yes, there is no mathematically exact method for choosing a particular grammar for the problem being solved. It is necessary to rely on experience and tests with errors. But the method works and often produces an acceptable result without an optimized grammar.

If someone is interested in the GoE, then here is the article of the authors of this method (maybe, I will soon translate).

Source: https://habr.com/ru/post/281334/

All Articles

Character regression and another approach

More articles: