RING buffer - 2D case

RING (ring) buffer - 2D case.
! NEW is a full-featured module with a guide, a link to github at the end of the article!

For a long time it was going to write on Habr several algorithmic tricks, gleaned from hobbies of the demo scene, from experiments with algorithms. I hope it will turn out in the old school spirit of the unusual use of interesting algorithms, because for me Habr is interested in just such articles.

The data structure of the RING buffer (ring buffer) is most often found in the implementation of network protocols, and in Concurrency structures (data synchronization between threads).
')
In this article, I would like to parse its implementation in client-side JavaScript. This language is very popular, and I have a lot of practice working with it. As an example, this can be used to work with terrain maps, real or game.

Let's start with what a ring buffer is and what it gives as an abstract algorithm:


1. The ring buffer allows you to get away from the dynamic redistribution of memory, but at the same time all the same to organize an effective sequential addition and deletion of data. In particular, for JS (as for all languages ​​with the garbage collector), this means a reduction in the work of the latter, which has a positive effect on performance.

2. The ring buffer allows you to get away from the actual data movement, in cases where you need to move the entire data array.
For JS, the push (elem) array manipulation methods are natively implemented, elem = pop () which add and remove an element from the end of the array, and shift unshift for similar work with the beginning. Alas, when working with the beginning of an array, the methods mainly work through the actual change of data, since in JS, data processing is based on hash maps. And the compiler can not always optimize the structure, due to ambiguity. In fact, the speed of modern computers in most cases is enough for such an implementation. But in the example, which I will analyze below, we will go a little further.

What could be interesting here, you ask? The fact is that the canonical algorithm of the ring buffer adapts remarkably to the 2D case, which we will analyze (both in 3D and in general on any dimension of the array).

I am sure that such a generalization of the structure is not new, but I did not find its explanation on the Internet, and implemented it myself.

- The buffer object will encapsulate the storage of the actual data, representing it as a two-dimensional array of constant size.
- The considered algorithm will be able to add / read two-dimensional data (for example, data about the surface of a game map with a seamless load of locations).
- The push method, regardless of direction, will work for a time that depends only on the number of actually loaded O (n) elements, and not on the buffer size O (n ^ 2), where n is the length of the side of the square buffer. Multi-pass (streaming) buffer filling, if needed, will not impose an additional load.

First, let's see how the buffer looks outside (from the “sliding window”):



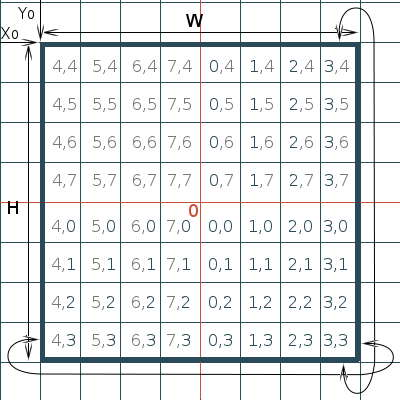
The figure shows a window sliding relative to the buffer, equal to it in size.

The window here refers to the scope of the space. Can be implemented for a larger buffer. (This is relevant for streaming preloading of location data so that the data is loaded ahead of its actual display in the window). The window has a positioning point X0, Y0 in the coordinates of the game world, as well as the width W and height H, (in this implementation, they will be equal to a power of two, and equal to each other). Red lines indicate the “seam” of the buffer. In the figure it is in the middle for clarity. Take a look at the indexes, they clearly show the real position of the data in the buffer. When the window shifts, the data does not move across the cells in the buffer; instead, the seam is positioned.

Simultaneously with such a manipulation, data cells that are out of view of a window, the data of which no longer needs to be, turn out to be from the side in which the window moves, and from which the new data should be issued to the memory cells. This links the process of deleting old data + writing new = in one operation. It remains to record the new data in the window. Regardless of where the seam is located, api buffer will take over the correct mapping in memory. In practice, we even implement four modes of push (data) operation to automatically “push in” data.

Implementation:

It would be possible to write an algorithm in many ways, including supporting any buffer size, but since I started all this for optimization, I will demonstrate the implementation through bitwise operations. The only overhead restriction of which will be the need to use the size of the buffer side, equal to the power of two. This is quite normal practice in game engines.

We note and strictly define the following pattern:

As the viewport is shifted, the buffer does not shift, but is gradually overfilled with data from adjacent zones. These zones will be located on the space grid, a multiple of the buffer size.

We agree to determine the initial positioning of the buffer from world coordinates such that this grid would pass through (0,0) on the world map.

Without really relying on my eloquence, I enclose an explanatory picture:


(thick red line marked world zero)

The usefulness of this additional abstraction is expressed not only in the fact that:

- the world coordinates of the data falling into the cells will always fall into the same places, but also that
- The coordinates will be relative to the specified zones, which in turn gives greater flexibility in storing these data. They can be stored both monolithically and in parts, up to the cluster implementation of the server.

In fact, you will certainly need something like this if the map on the server is really large. So this is a good bookmark for extensibility.

But back to the main reason. Such a realization, in the case of a buffer with a side size multiple of a power of two, makes it trivial to convert world coordinates to relative ones and vice versa. Just because the relative coordinates in this case are always in the lower absolute bits. And in the higher bits are the coordinates of the zones.

Usually in low-level algorithms it is highly desirable to strive for implementation through bit operations, since they are the fastest. On some architectures, they are even faster than addition (mostly true for microcontrollers).

<script> var Buffer2d = function(side){ //   (! !)  . var x0 = 4, y0 = 4, //   ,   .1 (4,4) msk = side - 1, //  ,      buffer = []; while( buffer.push( new Array(side) ) < side ); //  ...  JS     . //     ,          . for(var y = 0; y < side; y++) // DEBUG:       : for(var x = 0; x < side; x++) buffer[y][x] = x + ',' + y; return { get : function (x,y){ return buffer[y + (y0 & msk) & msk][x + (x0 & msk) & msk]; } } } var side = 8; var myBuf = Buffer2d(side); for(var y = 0, n = 0; y < side; y++, console.log(str)) // DEBUG:       .1 for(var str = ++n + '\t\t\t', x = 0; x < side; x++) str += myBuf.get(x,y) + '\t'; </script> 

At this stage, the benchmark provides an analogue of Figure 1 to the console using sequential access to the buffer via the Buffer2d.get (x, y) API function.

Now we add directly the ability to push new data to the buffer. First we need a dynamic render:

 onkeydown = function(e){ var vect = { 37 : -1, //lookup table -         38 : -side, 39 : +1, 40 : +side}[ (e || window.event).keyCode ]; if(vect===undefined) return; for(var data = [], n = 0; data.push(n++) < side;); myBuf.push(data, vect); console.log('\n'); for(var y = 0, n = 0; y < side; y++, console.log(str+'')) for(var str = ++n + '\t\t\t', x = 0; x < side; x++) str += myBuf.get(x,y) + '\t'; } 

What is the vect parameter?

Is the displacement vector, recorded as the sum of the horizontal and vertical displacement digits.
- such a form will allow us to further unequivocally indicate not only single offsets, but also to another vector, for example, diagonally.

Now we need to write the most difficult part (although it may seem difficult only because bit operations in applied algorithms are now “not fashionable”).

In this part of the code, we must place all the incoming data on the cells, the values ​​of which, as a result of the buffer offset, become unnecessary. Here I will not describe the mechanisms for the operation of bit operations; this topic could take a separate article.
Let me just say that to understand this code, it will be necessary to understand such an operation as “taking bits by mask”, and what is in this implementation is the same as “taking by module” of a power of two.

In the object returned by the Buffer2d constructor, add the method:

  push : function(data, vect){ // vect   +-1  right|left, +-side  down|up var dx = ((vect + side / 2) & msk) - side/2, dy = (vect - dx) / side; x0 += dx; y0 += dy; for(var y = Math.min(0, -dy), y2 = Math.max(0, -dy), n = 0; y < y2; y++, n += side) buffer[y0 + y & msk] = data.slice(n, side); //     for(var x = Math.min(0, -dx), x2 = Math.max(0, -dx), y2 = y + side; x < x2; x++) for(; y < y2; y++) buffer[y0 + y & msk][x0 + x & msk] = data[n++]; //    } 

If you want to try running this code, do not forget to open the developer tools in your browser.
The code is tested, everything works, the buffer is output to the console! Control keyboard arrows.

If someone noticed that the written API for the buffer is capable of shifting it more than one cell at a time - I did not test the Unit test for this case, but yes, it should be able to!

That's probably all. I tried to write intelligibly. Write in the comments, if I have not noticed any errors, I will be very happy with the advice. I hope the article pleased you.

NEW on github