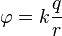Formulation of the problem

The other day I saw on the Internet a very curious thing: the Mendo engine. A rotor on bearings of extremely low friction: the original had a glass cylinder suspended on two needles, modern ones have a magnetic axle suspension. The motor is brushless, solar panels are suspended on the rotor, which give voltage to the coils wound on the rotor. The rotor turns in a fixed magnetic field of the stator, the solar battery moves away from the directional light, in its place comes another. It is an extremely elegant solution that everyone can make at home.



Here in this video the principle of work is described in great detail (in Russian):





')

But the next thing seemed to me even more interesting than the engine itself. In the description of this video, Dmitry Korzhevsky wrote the following thing: “It is IMPOSSIBLE to replace the side support with a magnet !!! Don't ask this question again! ”







Excuse: I am never a physicist, I can be very wrong, corrections are welcome.







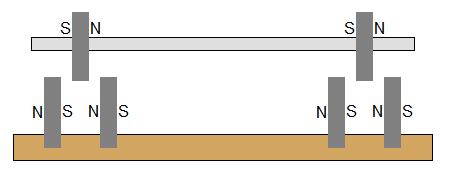
Oh, this is interesting. Let's look again at how the magnetic rotor suspension works. If we put two magnets, the potential isoline looks as follows depending on the distance between the two magnets:







That is, we put two fixed magnets on the stator. The magnet on the rotor axis will not want to move sideways, since the potential isoline has a local minimum. He wants to jump along the axis of the rotor. We make two such systems, we get the rotor axis, which is fixed by a magnetic field in the radial direction, but at the same time is unstable in the longitudinal direction. We rest the axis into the glass wall and voila, we received a bearing of weak friction.



But the glass wall is somehow ... inelegant, is it? It is quite logical to get a rotor completely floating in the air, without any crutches. And obviously Dmitri zatyukali this issue, so much so that he was forced to write the impossibility of this directly in the video description. And after all, Dmitry Korzhevsky is not the only one.



Let's look here, I quote:

What would happen if the base magnets were spaced and like in this drawing? With the mirror requirement?

Or here I quote:

Why is it a motorcycle? It would be useful to make it out. I attached a very rough jpg of what I mean. the green magnets are what am im referring to. is there some theory or law preventing this?

That is, people around the world want to get rid of the mechanical support of the axis. I studied poorly at school and the impossibility of creating a fully magnetic suspension without crutches is also never obvious to me. On occasion, while drinking a cup of tea, I asked my boss, a world-renowned scientist (not physics, applied mathematics), the question: “Why, actually impossible?” And you know, this was not obvious to him either!



In the above forums, no one really explained why this is impossible. At best, some Irnshaw theorem was quoted, which is not very digestible. So, it reads as follows: “Any equilibrium configuration of point charges is unstable if, apart from the Coulomb forces of attraction and repulsion, nothing acts on them.” Do you understand? I do not. Suppose I can accept the fact that we are talking about charged particles, and not about magnets. But what next?

First illustration

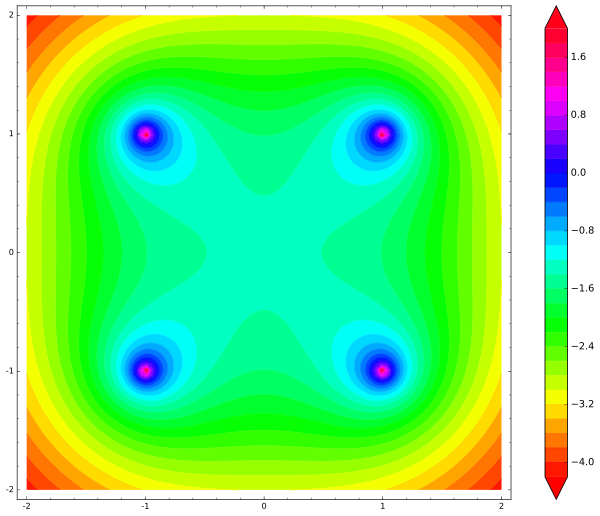
When something is unclear to me, I draw a picture. For simplicity, it will be in two-dimensional space. Let's imagine four fixed unit charges at the corners of a square and a free charge at the center of the square. Like that:







Is a free charge not in a state of stable equilibrium? After all, wherever he moves, he approaches one of the fixed charges, increasing the repulsive force! Let's try to draw a free charge potential energy map. I was a bad student at school, I missed physics, so we’ll draw on Wikipedia. So, if we have only one fixed charge in space, then it creates electrostatic potential in the whole space.

The formula of the electrostatic potential (Coulomb potential) of a point charge in vacuum:

In all speculative experiments, all my coefficients are either zero or one. Therefore, the charge q is unit, unclear k is also one. That is, one fixed charge creates a potential, measured by the formula 1 / r, where r is the distance to the charge.



The potential energy of a free unit charge in the field of our fixed charge is also 1 / r. (Generally speaking, the energy is equal to k * q1 * q2 / r, but the coefficients are chosen so that it is convenient to count). For multiple charges, all potentials simply add up.

Let's draw the potential energy map of our free charge, I do it with sage :

var('x,y')

def unit_potential(a,b,x,y): return 1/(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y)

contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True)

, , :







. , , , . ? , . , . , . , , ?



, , -ln r, r — , 1/r. , :

var('x,y')

def unit_potential(a,b,x,y): return -ln(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y)

contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True)

:





, . — , , . , , .

, ?

, , - . . , . , , . . , , .



, , ! :



1. , . , « » : .

2. — , . , .. , .

3. : , , , .

4. : , . , .



, E B, . — , (x,y,z,t), . , E(x,y,z,t). , , E . , , .



, E ( ) .



? : E ( ), u, ( !) «» , E. , u, E.



: . ,

«», , , . , , E .



, E — u. , , u . — «» . — . (, ). — . , . , :







( ) . , , :







, ( ) . :







. . , , , . . , — , ( , ) .



1/r , ! , , . 2D -ln r.



Update: chersanya, .

, . , , , . . , . ? ?



, , . , :







, (), , , . ? :

var('x,y')

def unit_potential(a,b,x,y): return -ln(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y)

contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True)

? ( ), . . , , , . — :

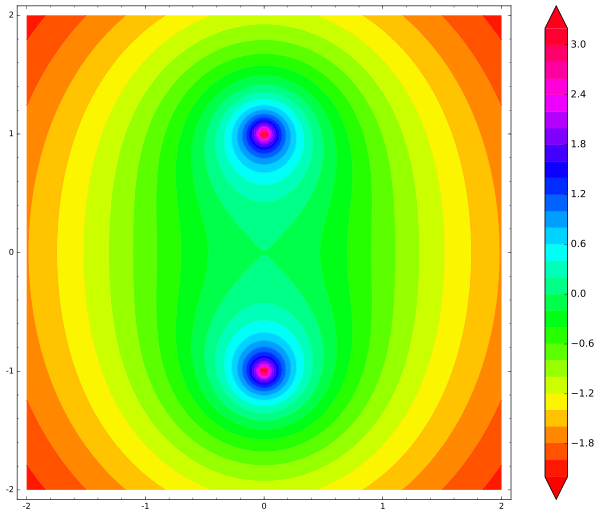
var('x,y')

def unit_potential(a,b,x,y): return -ln(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y)
def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y)

contour_plot(energy(x,y), (x, -3, 3), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True)

, ( ). , . !



, ? . , — . . , ( !) !

, , . , . , , .



? ( ) .



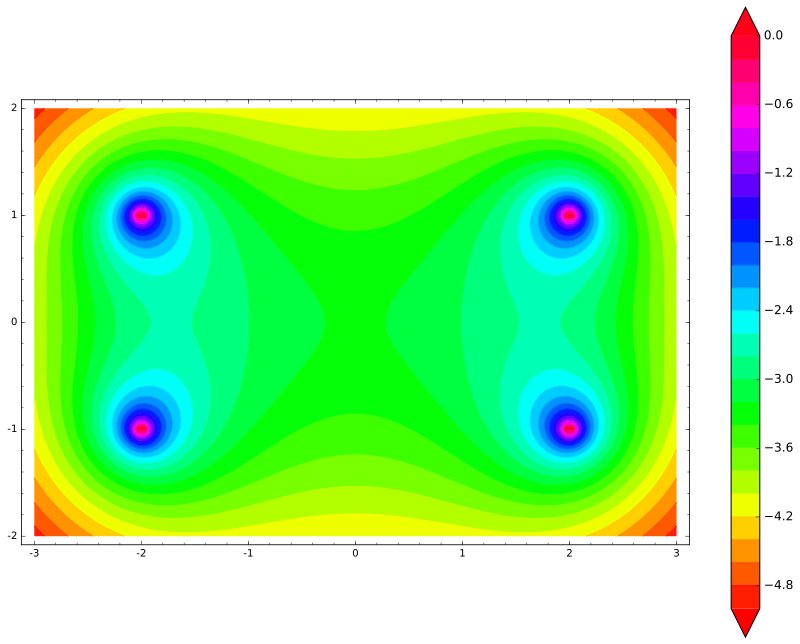
1.

2.

3. ,



, . , , !

Update:

, . .