Superscalar stack processor: details

Continuation of a series of articles that analyze the idea of ​​a superscalar processor with OoO and a stack machine front end
The topic of this article is function call, inside view.

Previous articles:
1 - description of work on a linear piece
2 - function call, save registers

By focusing in the last article on the outside of the function call, we lost sight of how it would all be executed inside. The author does not consider himself a specialist in hardware, but he still foresees problems.
')
We mentioned that after returning from a function, I want to get the processor in the same state as before. And it is precisely for this that they preserved the state of the registers. But the state of the processor is not only registers. but also queues of mopov, condition of conveyors ...

Imagine a situation where at the time of a function call we have:

• some number of mops in the decoder stack
• mops removed by the decoder from the stack but waiting for the parent mop to be executed
• mops on the performance in conveyors

As a result, it is impossible to just start the execution of a new function because

• for this, it may be trite not enough mops - those that remain from the parent function will not be released until we return from this
• The stack of mop indexes in the decoder has a fixed depth and can easily overflow during recursion or just a long chain of calls.
• mops in pipelines will be executed after (after calling a new function) the numbering of registers changes

It may seem that we have taken certain measures to avoid the problems described when declaring a function call with a generalized instruction, which must wait for the call to calculate all its arguments.

However, there is a problem with the fact that the decoder will have time to process the code after calling the function, if it is independent of the data. For example:

int i, j, k; … i = foo (i + 1); j += k; bar (i, j); 

After returning from foo, we cannot rely on the fact that j managed to be calculated and saved (and then restored) in the context of the current task, nor on the fact that the mops survived from j + = k; if she did not have time to calculate.

Suppose, after seeing the function call, the decoder stops its operation until it returns from this function. Then how to deal with this situation:

  int i, j, k; … bar (foo (i + 1), j += k); 

One decoder is not enough. It seems that after returning from a function, you simply need to start decoding and executing further code again.

But after all, basically, these problems caused by superscalarity are not unique to our architecture, you may not need to reinvent the wheel, but it’s worth seeing how it has already been solved before.

Ok, let's take a look at Intel's Sandy Bridge (thanks to Takit Murka aka Felid )
and also here

Sandy Bridge.

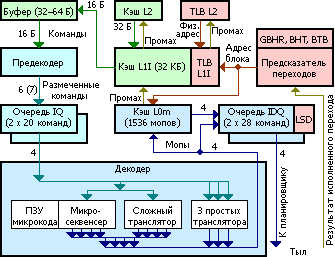
Presumably, the Sandy Bridge frontend,

• executable code enters the precoder buffer (in the upper left corner of the circuit) from the instruction cache of the first level (L1I)
• Precoder can process up to 7 instructions per clock, depending on their total length and complexity
• marked commands fall into one of two command queues (IQ) - one for each thread (hyperthreading), for 20 teams each
• the decoder alternately reads the commands from the queues and translates them into mops
• depending on the type of command, the decoder uses different types of translators
• the decoding result goes to the mop cache and two hyperthreading buffers
• the aligned pieces (portions) of 32 bytes of the source code are cached, while:
  
  • the key is the entry point in the portion, if there were transitions to different places in one portion, this portion will be multiplied in the cache
  • portion decoding starts at its entry point
  • only portions that spawn no more than 18 mop are cached - 3 lines of 6 mop each
  • the instruction, divided by the boundary of two portions, refers to the first of them
  • from the portion it is allowed to have no more than 6 transitions, only one of them can be unconditional - and the last at the same time. This is important because a function call is an unconditional transition and everything that happens after it does not fall into the current caching unit, and therefore will not be executed until we try to go back.
  • if the portion does not end with an unconditional transition, a transition occurs to the first instruction of the next section address
  • The mop cache (L0m) is synchronized with L1I, the last cache line is 64 bytes, so that when you push out the L1I line, everything related to two portions is deleted from L0m
  • just curious, L1I works with physical addresses, L0m - with virtual
• As for speculative execution:
  
  • The predictor of transitions (BPU) is able for a conditional transition mop to report the probability of the occurrence of an event of this transition
  • because in the current queue of mops, the decoder has already identified all potential transitions, you can check them
  • if the transition probability is high enough, it makes sense to preload the necessary portion of code in advance and execute it speculatively
  • if the transition really happens, we will get at least a decoded piece of data, perhaps part of the instructions (which have no data dependencies) will have time to complete
  • if there is no transition, instructions that have not yet been completed should be removed from execution, those that have managed to work out should not have irreparable consequences. All captured resources are released.
  • so, they will be executed in a special speculative mode:
    
    • memory should be deferred
    • reading from memory is performed only if data is already in the data cache, otherwise execution is blocked (in order to avoid useless cache misses and subsequent access to the swap)
    • everything that can cause an exception (division by 0, for example) is marked accordingly and is also blocked, however, this is a generalization of the previous paragraph. Now, when the transition occurs, we can honestly restart the blocked mops
    • and, of course, it is worth recalling that all this is only speculation, only Intel knows the real picture

How does the function call occur?
Let us examine the following example.

 int i, j, k, l, m, n; ... i = 1 + foo (1 + bar (1 + biz (1 + baz (1 + j) + k) + l) + m) + n; 

We will naively assume that all this code will be located in one 32 byte chunk and the order of code generation (with the optimizer disabled) will correspond to the order of the text. Mark the code according to which instance of the section it will be in the L0m cache:

 int i, j, k, l, m, n; ... 1> i = 1 + 4> foo ( 1> 1 + 3> bar ( 1> 1 + 2> biz ( 1> 1 + 1> baz (1 + j) 2> + k) 3> + l) 4> + m) 5> + n; 

This fragment seems to take 5 cache lines out of 256 available.
It is not surprising that the compiler tries its best to inline small functions.

findings

So, we looked at how functions are called in one of the highly sophisticated micro-architectures, what benefits can we derive from this?

Select the objective points:

• The instruction cache is needed; without this, no intelligible processor is possible.
• The cache has a granularity, at the moment the typical size is a string of 64 bytes.
• Decoding (for x86_64, at least) is a rather expensive operation, it makes sense to cache the decoded code as strings of mops
• Access by entry point is a great idea if it is possible to do without reproduction of records at the same time - the question of implementation
• No more than one mandatory exit - a simple and natural solution, eliminating a lot of problems

It may seem that all this will work for our architecture with a stack frontend. But there is a nuance.
Let's explain with an example. Here is Ackermann 's function :

 int a(int m, int n) { if (m == 0) return n + 1; if (n == 0) return a(m - 1, 1); return a(m - 1, a(m, n - 1)); } 

It looks simple, but it demonstrates the wonders of recursion. The following graph shows the dynamics of the nesting depth for the call to a (3, 5), the x number is the step number, and the y number is the call depth.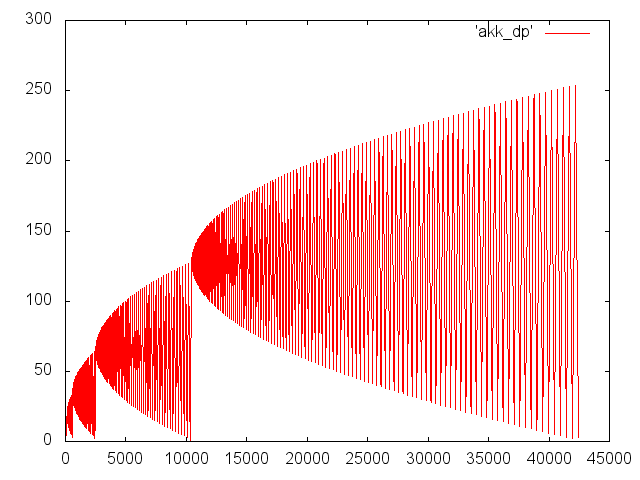

Since we decided to consider the function call as a generalized instruction with an arbitrary number of parameters, in the case of m * n! = 0, the first argument (m-1) will remain on the stack of the mops, while the second argument will be calculated: a (m, n- one). Well, if the first argument has time to be calculated and its value will be saved when called in the register stack. But it may happen that the expression for the first argument will be evaluated longer than the arguments of the child call in the second argument. And then we will hang in considerable quantities incomplete mops.
The parent call mop will also wait until the child call is completed. Call depth can easily reach (tens) thousands of units, for example, SandyBrige simply doesn’t have as many mops.

The essence of the problem is that, recognizing the call as a generalized instruction, we thereby recognized the program as a generalized expression. And the tree of this expression, due to recursion, can be of any height. On the other hand, the expression stack is limited. And the elements of the stack are the indexes of the mops, of which there is also a limited number.

But we are not accustomed to surrender so easily, that’s why B.’s plan comes into play.

Plan b

Register superscalar processors have no such problems. Identification of connections between mopami occurs later - at the stage of renaming registers.
We have these links are stored in the stack of indexes mopov.

Maybe save the stack state? To keep the mop indexes a little, as we found out, the mops themselves also need our care. It seems natural to organize the preservation of mops through a stack, allocated or not, the question is completely separate.

And here we are faced with the same problems that we encountered when trying to save registers. Namely, with a single (for all functions) identification of mops:

• order of use of mops depends on the history of calls
• inside the function it is determined dynamically
• there are no guarantees that after the FILL operation we will not get a conflict with the already occupied mop

The way to solve these problems is the same:

• mop ring buffer
• for each function its own numbering of mops, for example, 0 ...
• FILL and SPILL are made for the whole function, which allows, if necessary, to bind the stack of registers and the stack of mops to one memory area.
• FILL and SPILL are done only for mops waiting to be completed, therefore, a mask (or enumeration) of serialized mops fits into the stack.
• stack of mop indexes we also need to save

At first glance, the need to drive decoded mops through memory seems monstrous. But when the catecholamines burn out, it becomes clear that the scale of the disaster is not so great.

1. although in modern processors, the parameters (at least part of them) are passed through registers, when recursively calling, the parameters are saved and there is no place except on the stack, besides:
   
   • return address and frame pointer are also saved in the stack
   • volatile registers are stored on the stack by the caller.
   • non-volatile registers are also stored in the stack, but by the called party
2. expressions like 'a (m - 1, a (m, n - 1))' the compiler can break up by introducing (explicitly or indirectly) a temporary variable equal to a (m, n - 1). This reduces the number of mops that need to be saved.
3. all the failed conditional branches at the time of the unconditional transition, which is a function call, we have already thrown out
4. we can also throw out all the mops for the upcoming call or simply do not load them using a technique similar to that in SandyBridge
5. and we can leave, then upon returning from the function, we get a bonus ready for execution or already even partially executed (data independent) code
6. in the most "economical" version, only one serialized mop call will fall onto the stack, and this is not much different from passing the frame-fuffer address, for example
7. (de) serialization of mops does not look like a costly operation, moreover, it can be done in the background, in advance, without blocking the current return from the function
8. storing mops on the stack along with loading is supposed to be an alternative to the l0m cache, which is no longer needed
9. the size of the serialized mop is not too large, for SandyBridge the initial size of the mop is estimated to be a maximum of 147 bits, compressed - 85 bits (and there are also x87, SSE and AVX of all stripes)
10. the fact that the processor’s technological features are accessible from the outside and any technical secrets can be compromised, doesn’t scare the author. In the end, let the processor xor'it this data with a one-time notebook.

What's next

Until now, we have not paid attention to the weak point of all stack machines — redundant memory accesses.
Here we will deal with them in the next article .