Nothing is so hidden from us as that which lies on the surface.
Sun Tzu and Zhuge Liang (free translation)

Foreword

')
This happened in one of the videos on YouTube. When viewing a programmer’s lesson, it was necessary to urgently translate 377 into the decimal system. We did not lay it out on triples of bits, represent degrees of the eight, or just ignore it and skip this unimportant moment. We launched a calculator in the operating system, pushed its window to the center of the screen and found out everything there. Yes, this is it - the number 255.

Of course, you do not need to tell what happens in more complex cases. Sometimes it comes to a leaf in a notebook, lying next to the computer just for such cases. Everybody has a parabola or something like that intersecting something about that.

First contact

As you would expect, using Emacs for months or just for many years comes Emacs of the brain. Therefore, such cases do not pass in vain and the question arises in the middle of the night: “How can I translate 377 in Emacs? Does he even know how? Well, at least 8 will raise a degree? ".

The next morning, charged with energy in the form of tea with a handful of chocolates, we open Emacs and begin its research.

We start with operations

It is clear that by entering Alt + x and calc, the first thing we see is the usual stack calculator, which was written, probably, by a hundred of these hands here. And I would not like to repeat this path a hundred and first time, finding that he does not know how.

At random we first do + - * /

5 <RET> 7 <RET> +

5 <RET> 7 <RET> -

5 <RET> 7 <RET> *

5 <RET> 7 <RET> /


Then

8 <RET> 8 <RET> *


ABOUT! And here is the square of the eight! And where is the square, there is a cube!

We open a help

Of course, everyone knows that a Russian person (USSR, imperial, etc.) will not start with instructions, but first he will try to break everything, then fix it, and then read the instruction in search of the missing secrets.

I will not say that this time everything started with instructions, since, unlike many others, I don’t turn off the Emacs menu, but I use it to recall keyboard shortcuts in all rare modes.

So this time I started the review from the calculator menu



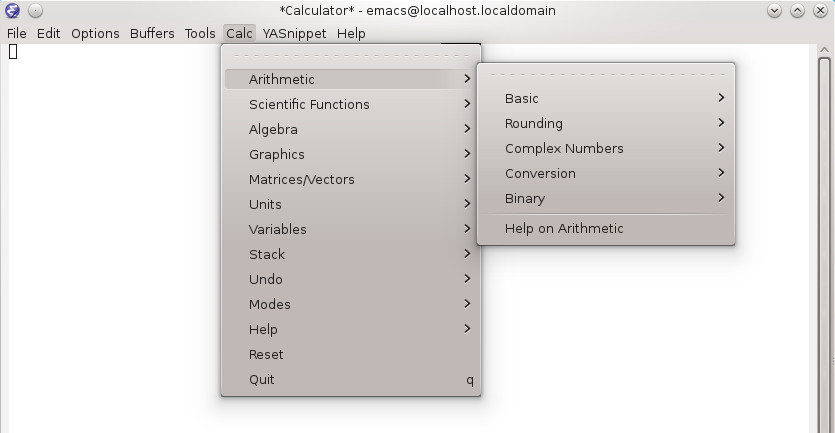
In order to open the help, you need to enter Ctrl + x + * + i. And to open a tutorial, you need to enter Ctrl + x + * + t.

They can be opened in different ways, but, as practice has shown, the combination Ctrl + x + * + <key> is used very often and is made specifically for convenient control of the calculator during other work.

Therefore, you can open the calculator using Ctrl + x + * + c, and you can start the calculator in the current buffer using Ctrl + x + * + e.

Raise the bar

About a day went to check all the options from the menu. Among them there are such as finding the next prime number, so this could not be simply missed, I wanted to make sure that it really worked.

The greatest common divisor (GCD) can now not be written, here it just is. You must enter two numbers and press kg, where k means combinatorics, and g - gcd (Greatest Common Divisor).

The factorial 3000 (a kind of speed check) is not easily calculated, but it is still calculated in fifteen seconds.

The transposition of the matrix, finding its determinant or scalar multiplication of vectors is performed easily and with a whistle.

For a minute, I forgot what I came for, performing operations one after another, not believing my own eyes. And for what did I come?

We continue

On the second day, it became interesting whether he calculated the system of equations by the Cramer method. Once there are determinants, then the Kramer solution can be found. Previously, I wrote this many times in the editor, even the skills have already developed on the calculation of the determinants in the editor.

But this was not required. It turned out that it is enough just to enter three equations, and then request their solution. Yes, just like in Wolfram.

Find the first available system

2y + x + z = -1
-z - y + 3x = -1
-2x + 3z + 2y = 5


You just need to select it Ctrl + x + h, copy Alt + w, go to the calculator Ctrl + x + * + *, paste it Ctrl + y, pack the equations into the 3 vp vector, press a P and in response to the question “By what search for roots? ”enter xy z.

A vector with answers appears in the stack, then we simply press y and the vector with answers is inserted at the cursor position in the original buffer with equations.

[[ 0., -2., 3. ]] 2y + x + z = -1
-z - y + 3x = -1
-2x + 3z + 2y = 5


If we left the cursor at the end of the system of equations, the answer would be inserted there.

It's time to turn around

Stack power

When using the calculator for some time, it becomes inconvenient because values ​​start to accumulate on the stack. At the same time, you do not know whether it is possible to remove them, since there are the necessary ones among them, therefore any experiment may result in loss.

So the clock goes on, until in one wonderful moment you decide to open the help and spend time reading it. Fortunately, all combinations are selected as conveniently as possible, so that there is even some symmetry of actions present and maintained.

These numbers with colons in the stack at the beginning of each line are like addresses. In many commands, entering a positive argument means “a few pieces,” and entering a negative argument means “such a number”.

For example, we have the number five on the stack.

1: 5


If we press <RET> (Enter), it will be copied and we will have

2: 5
1: 5


This two is equal to the number of elements in the stack, it is also the address of the first number five, and the number 1 is the address of the second number five.

The <RET> command has an argument that defaults to 1. When we press <RET>, it copies as many items from the top of the stack (the top is at the bottom). Therefore, if we enter Alt + 2 + <RET>, it will take two elements and copy them.

4: 5
3: 5
2: 5
1: 5


If the argument is negative, then it takes an element with such an address (if the minus is removed). Therefore, if we now enter Alt + - + 4 + <RET>, it will copy the element at 4

5: 5
4: 5
3: 5
2: 5
1: 5


Most of the basic operations work in the same way. If you need to delete three elements, then we write Alt + 3 + <DEL>, where <DEL> is the backspace. If you need to delete an element with the address 3, then we write Alt + - + 3 + <DEL>.

If you read the help in more detail, then these operations can be found such original operations from the anti-world, consisting of black matter. For example, for <RET> there is a Ctrl + j operation, for <DEL> there is Alt + <DEL>, and for <TAB> there is Alt + <TAB>.

The meaning of these operations is exactly the same, only the argument changes in sign. Therefore, if you enter Alt + 3 + Ctrl + j, then it does not copy the three elements, but the element with the address 3, and if you enter a negative argument, it will not copy the element with the address 3, but three elements.

If you want to clear the entire stack, then you need to press Alt + 0 + <DEL>.

There are many ways

At first it seems that everything can be done only in one way, which you just need to learn. But over time, there are many ways to achieve the same result.

For example, how can I enter a matrix?

The very first thing that comes to mind is to write it in a buffer and then just copy it.

This

[[1, 2, 3], [4, 5, 6], [7, 8, 9]]


It turns into this

1: [ [ 1, 2, 3 ]
[ 4, 5, 6 ]
[ 7, 8, 9 ] ]


The second thing that comes to mind is the use of an internal remedy.

Matrix is ​​three vectors

1 <RET> 2 <RET> 3 <RET> 3 vp
4 <RET> 5 <RET> 6 <RET> 3 vp
7 <RET> 8 <RET> 9 <RET> 3 vp
3 vp


The third thing that comes to mind is the use of an internal and convenient means.

1 <RET> 2 <RET> 3 <RET> 4 <RET> 5 <RET> 6 <RET> 7 <RET> 8 <RET> 9 <RET>
[3, 3]
vp


And the fourth thing that comes to mind is “Can't you just enter it?”

[ 1 <SPC> 2 <SPC> 3 ; 4 <SPC> 5 <SPC> 6 ; 7 <SPC> 8 <SPC> 9 ] ]


The pack command has a symmetrical one - unpack, so if you need to decompose the matrix into vectors or decompose the matrix into numbers, then we just press v u.

We attract external funds

As you tinker with the calculator, you suddenly begin to pay attention to the surrounding buffers and the question gradually arises: “And what means of the usual Emacs can be attracted when working in the calculator?”

At first, we simply find the n-th derivative of a polynomial by writing a macro and repeating it n times through the macro argument.

For example, enter the expression

' x^5 + 4 x^3 + 2 x + 1 <RET>


Then press F3 to start recording the macro. Then press ad to calculate the derivative. Then to the question "For which variable?" We enter x. Then press F4 to finish recording the macro.

Do a cancellation of the calculation by pressing Ctrl +/ or applying the internal cancellation of the calculator - the letter U.

Having an initial expression

1: x^5 + 4 x^3 + 2 x + 1


Press Alt + 3 + F4 and as a result we have the third derivative

1: 60 x^2 + 24


If we press Ctrl + x + z, and then z z, then we will gradually get zero.

We leave to the outside world

After some time, the calculator closes and we return to our regular work, our usual entertainment.

And then at one point we read, in Emacs, of course, the story of a fox who jumped-jumped over a lazy dog ​​and jumped 1024 times. Wait, you say, unless a fox can jump right in exactly the same time, if it is not computer? It is necessary to fix this thing.

We have the following text

The quick brown fox has jumped over the lazy dog 1024 times.


Hover the cursor at 1024 and carefully press Ctrl + x + * + w. Next, press Q, and then just as carefully press Ctrl + x + * + w.

And we get

The quick brown fox has jumped over the lazy dog 32 times.


Now this is more like the truth. That is, in order to calculate something, the calculator does not have to be opened at all; you just need to press some buttons.

But the very thing

I remembered what I went for

Ctrl + x + * + *
8#377 <RET>
d 2
d 8
d 6
d 0
Ctrl + x + * + *


And finally

There was a time when I wrote a function on python

2016
1
1
Alt + - + 14 vp
255
+


I enclose here a list of units that he can convert, in the calculator, they are in u v.