Evaluation and optimization of computing performance on multi-core systems. Part 2

This publication is a translation of the second part of the article Characterization and Optimization Methodology of Applied to Stencil Computations of Intel engineers. In the previous part , a methodology was described for estimating the maximum performance that can be obtained using any algorithm on a specific platform using the example of a fairly common computational core used to solve a 3D acoustic isotropic wave equation. This part describes a series of steps to optimize source code for performance that is close to the expected benchmark.

In the next part we will talk about the genetic algorithm for auto-tuning, which allows you to increase the performance of the implementation by selecting the most optimal parameters for launching and compiling.

Standard Optimizations

Standard optimizations are optimizations aimed at improving concurrency, vectorization, and data locality. These 3 areas reflect the most important aspects for optimization on modern multi-core architectures. We implemented the following step by step:

dev00: Standard implementation of solving a 3D acoustic isotropic wave equation for validating results.
')
dev01: dev00 The implementation had a conditional jump in the internal loop to avoid data access errors at the boundaries of the area. Starting with AVX, such transitions are implemented using masks (masked instructions, such as VMASKMOVPD - approx. Translator). Thus, changing the boundaries of the cycles did not really affect the performance of the 2S-E5, while the Xeon Phi received 2-fold acceleration (Figure 7).

dev02: Cache blocking reduces the number of cache miss and only requires 3 new cycles (Figure 1). The disadvantage of this optimization is the addition of 3 new parameters to control the size of the block.

for(int bz=HALF_LENGTH; bz<n3; bz+=n3_Tblock) for(int by=HALF_LENGTH; by<n2; by+=n2_Tblock) for(int bx=HALF_LENGTH; bx<n1; bx+=n1_Tblock) { int izEnd = MIN(bz+n3_Tblock, n3); int iyEnd = MIN(by+n2_Tblock, n2); int ixEnd = MIN(n1_Tblock, n1-bx); int ix; for(int iz=bz; iz<izEnd; iz++) { for(int iy=by; iy<iyEnd; iy++) { float* next = ptr_next_base + iz*n1n2 + iy*n1 + bx; float* prev = ptr_prev_base + iz*n1n2 + iy*n1 + bx; float* vel = ptr_vel_base + iz*n1n2 + iy*n1 + bx; for(int ix=0; ix<ixEnd; ix++) { float value = 0.0; value += prev[ix]*coeff[0]; for(int ir=1; ir<=HALF_LENGTH; ir++) { value += coeff[ir] * (prev[ix + ir] + prev[ix - ir]) ; value += coeff[ir] * (prev[ix + ir*n1] + prev[ix - ir*n1]); value += coeff[ir] * (prev[ix + ir*n1n2] + prev[ix - ir*n1n2]); } next[ix] = 2.0f* prev[ix] - next[ix] + value*vel[ix]; } }}} 

Figure 1. Source code of the computational kernel with cache blocking.

dev03: To ensure that the variables are private for each thread, not only on each separate iteration, we divided the #pragma omp parallel and the #pragma omp for directives, appropriately declaring private variables between two OpenMP modifiers (clause).

dev04: #pragma ivdep directive can be used to prompt the vectorizer that the elements of an array within a loop do not overlap (i.e. there is no so-called pointer aliasing, which is often assumed to be the default for the C / C ++ compiler). The use of vectorization in this case can also be facilitated by using special compilation keys (-fno-alias) or using C / C ++ pragmas or Fortran directives.

dev05: Even if the compiler reports vectorized cycles, using the AVX instruction set extension (as well as using the ymm vector registers) may be inefficient. Accordingly, a manual scan of the cycles along with directives such as __assume_aligned (for telling the compiler that the arrays are aligned - for example, a translator) can improve automatic AVX vectorization (Figure 2).

 __assume_aligned(ptr_next, CACHELINE_BYTES); __assume_aligned(ptr_prev, CACHELINE_BYTES); __assume_aligned(ptr_vel, CACHELINE_BYTES); #pragma ivdep for(int ix=0; ix<ixEnd; ix++) { v = prev[ix]*c0 + c1 * FINITE_ADD(ix, 1) + c1 * FINITE_ADD(ix, vertical_1) + c1 * FINITE_ADD(ix, front_1) + c2 * FINITE_ADD(ix, 2) + c2 * FINITE_ADD(ix, vertical_2) + c2 * FINITE_ADD(ix, front_2) + c3 * FINITE_ADD(ix, 3) + c3 * FINITE_ADD(ix, vertical_3) + c3 * FINITE_ADD(ix, front_3) + c4 * FINITE_ADD(ix, 4) + c4 * FINITE_ADD(ix, vertical_4) + c4 * FINITE_ADD(ix, front_4) + c5 * FINITE_ADD(ix, 5) + c5 * FINITE_ADD(ix, vertical_5) + c5 * FINITE_ADD(ix, front_5) + c6 * FINITE_ADD(ix, 6) + c6 * FINITE_ADD(ix, vertical_6) + c6 * FINITE_ADD(ix, front_6) + c7 * FINITE_ADD(ix, 7) + c7 * FINITE_ADD(ix, vertical_7) + c7 * FINITE_ADD(ix, front_7) + c8 * FINITE_ADD(ix, 8) + c8 * FINITE_ADD(ix, vertical_8) + c8 * FINITE_ADD(ix, front_8) next[ix] = 2.0f* prev[ix] - next[ix] + v*vel[ix]; } 

Figure 2. Source code of the computational kernel with dev04 and dev05 optimizations. Here FINITE_ADD is a macro for the symmetric finite difference (FD) type v [ix + off] + v [ix-off].

dev06: Factoring the FD coefficients (c1, c2, ...) allows you to remove 2 multiplication operations for each of the coefficients. On 2S-E5, this change may decrease performance due to an increase in the imbalance of multiplications and additions. However, on the Xeon Phi in-order microarchitecture, removing “extra” instructions has a direct impact on increased performance, as noted in Figure 7.

dev07: Inconsistent memory access is a known effect on multi-socket platforms. On the current operating system, a typical memory allocation (for example, using mm_malloc) reserves the amount of space that will be needed, but physically the memory is allocated when it is first written / read into a variable. This rule (the so-called first touch policy), along with the pinning of threads (well-defined thread or process affinitization), allows developers to physically allocate memory pages on the same NUMA node on which the thread will use these memory pages in future calculations. This is achieved by placing the data at the first initialization inside a parallel region, where later they will be used for calculations.

dev08: For optimal use of registers, this implementation takes advantage of C / C ++ to support intrinsics specific to a particular processor architecture. An obvious disadvantage of this approach is some complexity and performance of the implementation only for the selected set of instructions. However, due to C macros, the code continues to be readable, as shown in Figure 5. This optimization has a greater impact on Xeon Phi than on 2S-E5, as shown in Figure 9. This is due to the implementation of SHIFT_MULT_INTR using _mm512_alignr_epi32 on Xeon Phi, allowing you to use right shift for 32-bit variables (in single precision). Thus, finite elements in the shortest possible dimensions can be calculated for a single vector using just 3 downloads as shown in Figures 4 and 5.

 #pragma ivdep for(TYPE_INTEGER ix=0;ix<ixEnd; ix+=SIMD_STEP){ SHIFT_MULT_INIT SHIFT_MULT_INTR(1) SHIFT_MULT_INTR(2) SHIFT_MULT_INTR(3) SHIFT_MULT_INTR(4) SHIFT_MULT_INTR(5) SHIFT_MULT_INTR(6) SHIFT_MULT_INTR(7) SHIFT_MULT_INTR(8) MUL_COEFF_INTR(vertical_1, front_1, coeffVec[1]) MUL_COEFF_INTR(vertical_2, front_2, coeffVec[2]) MUL_COEFF_INTR(vertical_3, front_3, coeffVec[3]) MUL_COEFF_INTR(vertical_4, front_4, coeffVec[4]) MUL_COEFF_INTR(vertical_5, front_5, coeffVec[5]) MUL_COEFF_INTR(vertical_6, front_6, coeffVec[6]) MUL_COEFF_INTR(vertical_7, front_7, coeffVec[7]) MUL_COEFF_INTR(vertical_8, front_8, coeffVec[8]) REFRESH_NEXT_INTR } 

Figure 3. The source code of a computational kernel with a macro containing int08 in dev08.


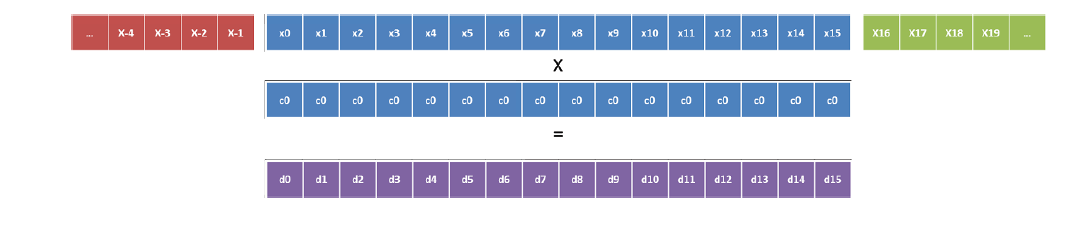
Figure 4. Vectorization in the shortest possible dimensions on Xeon Phi (coefficient c0).


Figure 5. Vectorization in the shortest possible dimensions on Xeon Phi (coefficient c1).

Now we are exploring the possibility of using AVX2 instructions for implementing equivalent optimization on a new architecture (at the time of publication of the article - translator's note) Intel Xeon E5 2600 v3. For the other two dimensions, vectorization is simpler. For one coefficient, we need only 4 loads, then the vectors are added together and multiplied by this factor (Figure 6). This is implemented as part of the MUL_COEFF_INTR macro.


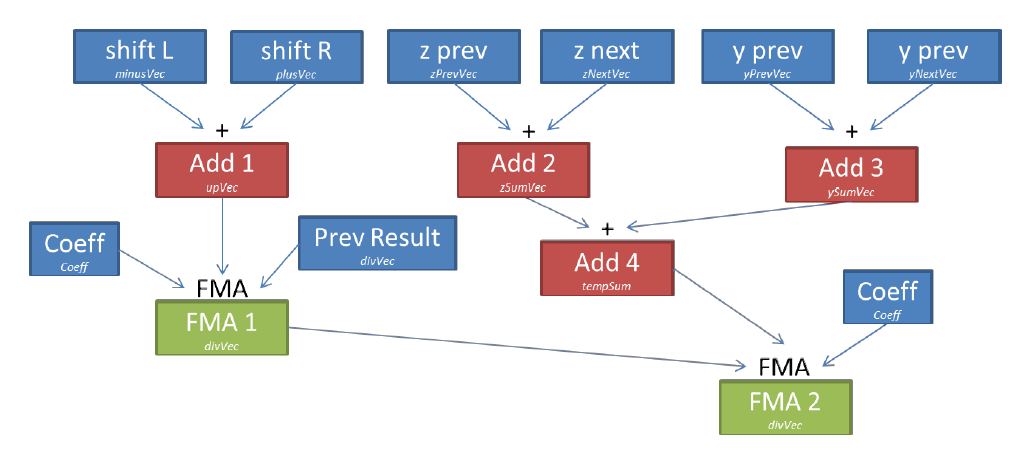
Figure 6. Operations for one coefficient in dev08.


Figure 7. GFlop / s performance in ECC off / Turbo on mode for Xeon Phi and Turbo on for Ivy Bridge.

dev09: On Xeon Phi, we can reduce the number of temporary variables, thereby reducing the number of registers required (so-called register pressure, which leads to spill / fill registers - approx. translator) using FMA instructions (fused multiply add). The coefficient can be written to the same register throughout all calculations (6 FMA) and the result of each FMA instruction is directly used for the next set of calculations, limiting the movement of data between registers (Figure 8).


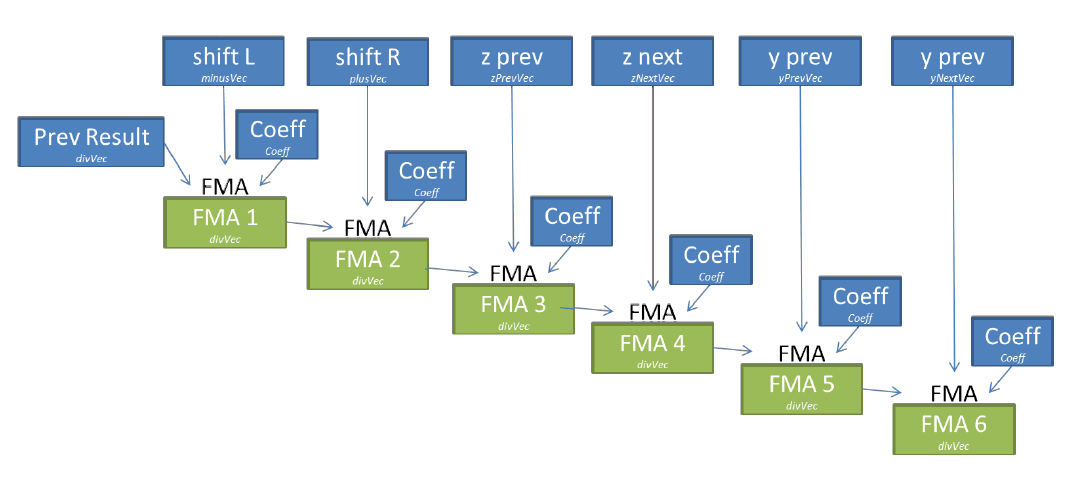
Figure 8. Operations for one coefficient in dev09.


Figure 9. Performance of various versions on the 2S-E5 Ivy Bridge and Xeon Phi. The most optimized version of dev09 has also been improved after applying the genetic auto-tuning algorithm.

To be continued…