Full-text fuzzy search using the Wagner-Fisher algorithm
The article is written about using the Levenshtein distance calculation algorithm for fuzzy search in the text, without using an auxiliary dictionary.
Levenshtein distance is used to compare two words or two lines to determine their similarity. Some time ago, I faced a similar task - to search for the occurrence of words, phrases and formulas similar to the pattern in a given line.
For starters, the Wagner-Fisher algorithm itself for calculating the Damerau-Levenshtein distance. You can read here and here .
Sample source code is from wiki .
It renamed row to column so that the illustrations coincide with the code.
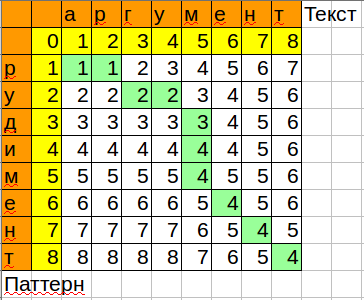
Formula to play in calc / excel:
Notice how the algorithm is optimized by memory, only the current and previous columns are stored.
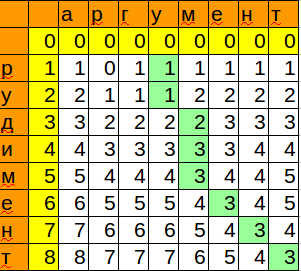
The search task differs from the comparison task in that it doesn’t matter to us what was before the match and what will be after. Because:
- the initial price of comparison with the current text symbol is zero, and not the position of this symbol
- the result is not the lower right corner of the table, but the minimum value in the last row
- optimization, in which the replacement of the text and the desired template can occur (if the required template is longer than the text), there is an extra
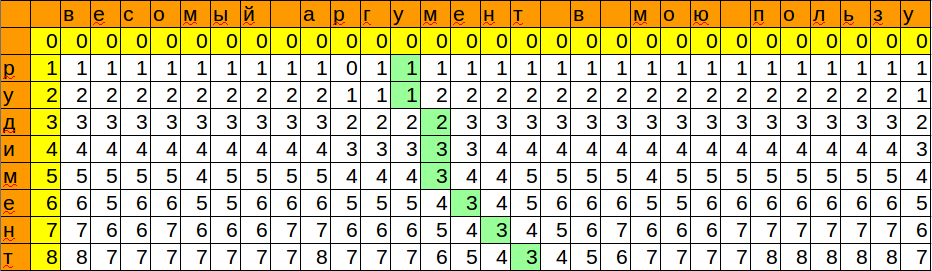
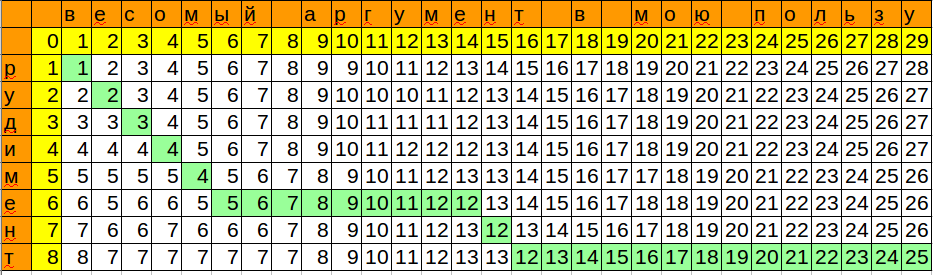
We remembered the position and the minimum value that we got when matching the pattern with the next character. Thus, we got a place where you can insert our word with minimal changes.
The final touch is to get all the information by coincidence.
PS: In the “Dark Room” it is easier to find the “Black Cat” than the “White Pit Bull”.
Levenshtein distance is used to compare two words or two lines to determine their similarity. Some time ago, I faced a similar task - to search for the occurrence of words, phrases and formulas similar to the pattern in a given line.
A little story of how such a mutation of the algorithm arose at all
After getting acquainted with the task, but before starting work on it, I went on vacation and went by train to my relatives. The road is not close - 8 hours of travel, no internet. What does a person usually have on the first day of vacation? That's right, the desire to work. Reflex.
I read about the Wagner-Fisher algorithm, but did not guess to save it somewhere (I was going on vacation). And so, under the sound of the wheels, I paint the matrix. How do you fall asleep when the editorial distance between words is not considered. After obtaining a satisfactory result, I write down the algorithm on a piece of paper and, with a sense of accomplishment of duty, I fall asleep.
')
The next day, after comparing the records and the real algorithm, I found in them a slight difference that changes the scope of the task. If the original algorithm is suitable for comparing two words and determining “how many characters of one word you need to delete / add / replace in order to get the second word”, then the mutant solves another problem - “how many characters of the first line need to be removed / added / replaced so that it goes completely in the second line. " I have not seen such implementations of the algorithm, if you apply somewhere - write.
I read about the Wagner-Fisher algorithm, but did not guess to save it somewhere (I was going on vacation). And so, under the sound of the wheels, I paint the matrix. How do you fall asleep when the editorial distance between words is not considered. After obtaining a satisfactory result, I write down the algorithm on a piece of paper and, with a sense of accomplishment of duty, I fall asleep.
')
The next day, after comparing the records and the real algorithm, I found in them a slight difference that changes the scope of the task. If the original algorithm is suitable for comparing two words and determining “how many characters of one word you need to delete / add / replace in order to get the second word”, then the mutant solves another problem - “how many characters of the first line need to be removed / added / replaced so that it goes completely in the second line. " I have not seen such implementations of the algorithm, if you apply somewhere - write.
For starters, the Wagner-Fisher algorithm itself for calculating the Damerau-Levenshtein distance. You can read here and here .
Sample source code is from wiki .
It renamed row to column so that the illustrations coincide with the code.
def distance(a, b): "Calculates the Levenshtein distance between a and b." n, m = len(a), len(b) if n > m: # Make sure n <= m, to use O(min(n,m)) space a, b = b, a n, m = m, n current_column = range(n+1) # Keep current and previous column, not entire matrix for i in range(1, m+1): previous_column, current_column = current_column, [i]+[0]*n for j in range(1,n+1): add, delete, change = previous_column[j]+1, current_column[j-1]+1, previous_column[j-1] if a[j-1] != b[i-1]: change += 1 current_column[j] = min(add, delete, change) return current_column[n] print distance(u'', u'') # 4 print distance(u' ', u'') # 25 

Formula to play in calc / excel:
=MIN(B3+1;C2+1;B2+IF($A3=C$1;0;1))
Notice how the algorithm is optimized by memory, only the current and previous columns are stored.
The search task differs from the comparison task in that it doesn’t matter to us what was before the match and what will be after. Because:
- the initial price of comparison with the current text symbol is zero, and not the position of this symbol
- the result is not the lower right corner of the table, but the minimum value in the last row
- optimization, in which the replacement of the text and the desired template can occur (if the required template is longer than the text), there is an extra
def distance_2(text, pattern): "Calculates the Levenshtein distance between text and pattern." text_len, pattern_len = len(text), len(pattern) current_column = range(pattern_len+1) min_value = pattern_len end_pos = 0 for i in range(1, text_len+1): previous_column, current_column = current_column, [0]*(pattern_len+1) # !!! for j in range(1,pattern_len+1): add, delete, change = previous_column[j]+1, current_column[j-1]+1, previous_column[j-1] if pattern[j-1] != text[i-1]: change += 1 current_column[j] = min(add, delete, change) if min_value > current_column[pattern_len]: # !!! min_value = current_column[pattern_len] end_pos = i return min_value, end_pos print distance_2(u'', u'') #3, 8 print distance_2(u' ', u'') #3, 16 

We remembered the position and the minimum value that we got when matching the pattern with the next character. Thus, we got a place where you can insert our word with minimal changes.
The final touch is to get all the information by coincidence.
def distance_3(text, pattern): min_value, end_pos = distance_2(text, pattern) min_value, start_pos = distance_2(text[end_pos-1::-1], pattern[::-1]) start_pos = end_pos - start_pos return min_value, start_pos, end_pos, text[start_pos:end_pos], pattern print distance_3(u'', u'') # 3 3 8 print distance_3(u' ', u'') # 3 11 16 PS: In the “Dark Room” it is easier to find the “Black Cat” than the “White Pit Bull”.
print distance_3(u' ', u' ') # 4 1 12 print distance_3(u' ', u' ') # 12 6 7 Source: https://habr.com/ru/post/279585/
All Articles