GF (256) final field and some magic

Introduction

As a student, I attend classes in cryptography. And of course this course could not ignore the standard AES .

When implementing this algorithm, the question arises about the implementation of GF (2 ^ 8) fields, which will be covered in this article. The following will be considered: bit magic for multiplying field elements, templates for generating tables of substitutions at the compilation stage.

The second part assumes that the reader has access to the C ++ 14 compiler. The first part will be written in the style of C.

Implementation

So, it is required to implement the following operations in the GF (256) field on the polynomial x ^ 8 + x ^ 4 + x ^ 3 + x + 1:

1. Multiplication
2. Finding the reverse

Let's start with the product of field elements:

The first thing that comes to mind is to implement the product of polynomials by a naive algorithm:

uint16_t polynomeMul(uint8_t a, uint8_t b){ unsigned rez = 0; for(int i=0; i<8; ++i){ rez ^= a * b&(1<<i) //    2  b_i * (x^i) * a(x) } return rez; } 

Then write the function of finding the remainder of the division by a polynomial.

At this point, I wondered what would happen next. And then I was waiting for an advanced Euclidean algorithm for polynomials, and although in fact it is not so bad, it was decided to think. Is it possible to make it somehow beautiful? It’s a pity not to use one operation to multiply two such polynomials, find the remainder of division by another.

Is it really impossible? Let's see what prevents us from realizing the product of polynomials through a simple product.

According to the formula for the product of polynomials we have:



For the product of two numbers in the binary number system, we obtain an almost analogous expression:



The difference is that for polynomials the expression determines the coefficient at .

A similar statement for the numbers will not be true due to the fact that in the previous discharge could overflow, changing the value of the considered.

How to get rid of overflow? Very simple. Consider the following entry:



Since, when multiplying polynomials of degree not higher than 7, a polynomial of degree higher than 14 cannot be obtained, the amount of no more than 15 zeros and ones will correspond to discharge (in fact, it is easy to make sure that it is not more than 8), which means that overflow is impossible. It remains only to convert the immediate sum to the sum modulo 2, highlighting the lower bit.

And so, if we represent a polynomial as a number in which each block corresponds to a block of 4 bits, then the work can be written as follows:

 uint64_t polynomeMul(uint64_t a, uint64_t b){ return (a*b) & 0x1111111111111111; // & 0b0001000100010001... } 

Now we analyze the product as elements of the Galois field.

Look at the polynomial . In the selected view, it looks like q = 0x100011011. The naked eye can see a large number of zero blocks immediately after the older block. When multiplying Q (x) by a polynomial we get a polynomial:



or a polynomial whose higher blocks are . This is what we will use to write the multiplication function:

 uint64_t galoisMul(uint64_t a, uint64_t b){ uint64_t mul = polynomeMul(a, b); const uint64_t basePolynome = 0x100011011; mul ^= polynomeMul(basePolynome, mul>>48<<16); //   Q(x)      (  4 ),     12   mul ^= polynomeMul(basePolynome, mul>>32); //        8 ,    .         mul. return mul; } 

With the multiplication figured out. Now you need to learn how to find the inverse element of it.

We recall that a field without addition and 0 forms a group of 255 elements. From this we obtain that for any element x there exists a number r equal to the size of the subgroup formed by this element, such that x ^ r = 1. Since the order of the subgroup is a divisor of the order of the group, which in turn gives us that . Then, according to the definition of the inverse element, we have :

 uint64_t galoisPow(uint64_t a, unsigned n){ //    . if(n==0){ return 1; }else if(n%2 == 0){ return galoisPow(galoisMul(a, a), n/2); // (a*a)^(n/2) }else{ uint64_t square = galoisMul(a, a); return galoisMul(galoisPow(square, n/2), a); // a * (a*a)^[n/2] } } uint64_t galoisInverse(uint64_t a){ return galoisPow(a, 254); } 

Everything? Oh yes, you need to be able to convert the original bytes into an extended form, in which we perform all operations. This can be done in the forehead cycle, but not today. The inner voice says you need to use a dirty trick. In the end, didn't I read the article thoroughly about counting single bits ?

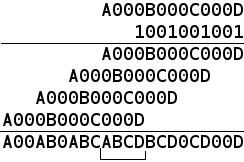
Let's denote byte as 0bABCDEFGH. The first thing that comes to mind is the multiplication by 0b1001001 of the three lower bits:

0bFGH * 0b1001001 = 0bFGHFGHFGH

0bFGHFGHFGH | 0b100010001 = 0bF000G000H, or three low-order bits fell into place.

Similarly, it is done over the middle three bits and the highest pair. The trick was coined. But three multiplications are like too much. Is it possible to do the same thing in 4 bits each? Having reviewed numerous samples of bits, I managed to find only one of the four that it works with:



Pay attention to the low bits of 7, 6, 1, 0 blocks. They are characterized by the presence of the desired bit in its place and, equally important, the impossibility of overflow due to the younger (relative to the data) bits.

As it was said, I did not find two paired fours bits. Failure? Not really. If we are able to put seven of the eight bits in their places using 2 multiplications, we can put all 8 by hoisting the last into its place by a simple shift.

 uint64_t extendToGalois(uint8_t a){ return (a & 0xC3) * 0x249249 & 0x11000011 | (a & 0x1C) * 0x1240 & 0x00011100| (a & 0x20) << 15; } 

With compression back things are easier. The following multiplication shows how to compress 4 bits:



With this in mind, the code takes the following form:

 uint8_t shrinkFromGalois(uint64_t a){ return (a & 0x11110000) * 0x249 >> 21 & 0xF0 | (a & 0x00001111) * 0x249 >> 9 & 0x0F; } 

Let compiler think

Why use rather expensive conversion bytes when you can use a table that has been calculated in advance? In this section, I will explain how to calculate it at the compilation stage using the magic of patterns using the example of a table of inverse elements by addition.

First of all, we ’ll add the constexpr qualifier to all previously written functions (from now on, compilation will require support from c ++ 14). This allows you to use these functions as template arguments.

 //      contexpr static uint8_t inverse(uint8_t x){ return shrinkFromGalois(GaloisInverse(extendToGalois(x))); } <p>template<int N, int… Data> class GaloisTable{ public: static constexpr auto& data = GaloisTable<N-1, inverse(N-1), Data…>::data; }</p> <p>template<int… Data> class GaloisTable<0, Data…> public: static constexpr uint8_t data[] = {Data…}; }</p> <p>template<int… Data> constexpr uint8_t GaloisTable<0, Data…>::data[];</p> 

Consider what happens when you try to use GaloisTable <256> :: data.

The compiler finds the corresponding template specialization, in which data is defined as GaloisTable <255, inverse (255)> :: data. It, in turn, is defined via GaloisTable <254, inverse (254), inverse (255)> :: data, and so on.

At each step, we have a pattern of the form: GaloisTable <m, inverse (m), inverse (m + 1), ..., inverse (255)>. And so on until m reaches 0.

When m reaches 0, the compiler manages to find a more specific pattern specialization (A compiler always prefers a more specific one). This is where the recursive task of the classes ends and from the sequence in Data ... the array itself is created, borrowed by all previous classes.

Data ... this step will be nothing more than inverse (0), inverse (1), ..., inverse (255), which we needed.

Conclusion : As a result, I would have killed significantly more time than I would have spent on a naive implementation (however, the majority of them were taken by the article itself). So when an idea comes to think, it makes sense to think whether to think.

Hope this article was helpful.

Update: Galua prefix replaced by Galois.